Archimedes (Archimedes of Siracusi, ancient Greek Ἀρχιμήδης, lat. Archimedes, c. 287 — c. 212 BC) considered finding a relation between volumes of a sphere and a cylinder, circumscribed around it, his main mathematical discovery. It is not casual that a ball and a cylinder were depicted on his grave.
Archimedes to Dositheus greetings! Shortly before this I forwarded to you some objects of my research, along with the proofs I have found […] I have now finished some other theorems I have thought of. some other theorems which have occurred to me, of which the most remarkable are these: […] the cylinder, which has as its base the largest circle of a sphere and a height equal to its cross-section, is one and a half of a sphere; and its surface is one and a half of the surface of a sphere. These properties undoubtedly existed in the said figures, but have not hitherto been noticed by anyone who has studied geometry…
Archimedes. On the sphere and cylinder.
When I was questor in Sicily I managed to track down his <Archimedes> grave. The Syracusians knew nothing about it, and indeed denied that any such thing existed. But there it was, completely surrounded and hidden by bushes of brambles and thorns. I remembered having heard of some simple lines of verse which had been inscribed on his tomb, referring to a sphere and cylinder modelled in stone on top of the grave. And so I took a good look round all the numerous tombs that stand beside the Agrigentine Gate. Finally I noted a little column just visible above the scrub: it was surmounted by a sphere and a cylinder. I immediately said to the Syracusans, some of whose leading citizens were with me at the time, that I believed this was the very object I had been looking for.
Cicero (c. 106 BC — c. 43 BC), Tusculan Disputations, Book V, Sections 64—66.
(Translation by Michael Grant in Cicero — On the Good Life, Penguin Books, New York, 1971, Pages 86—87)
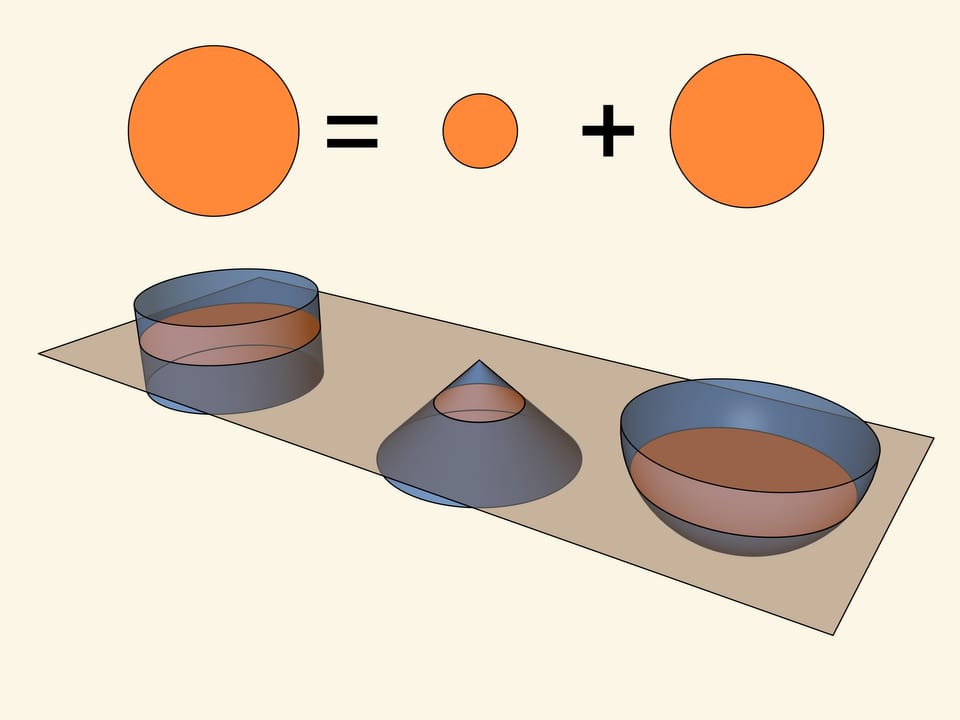
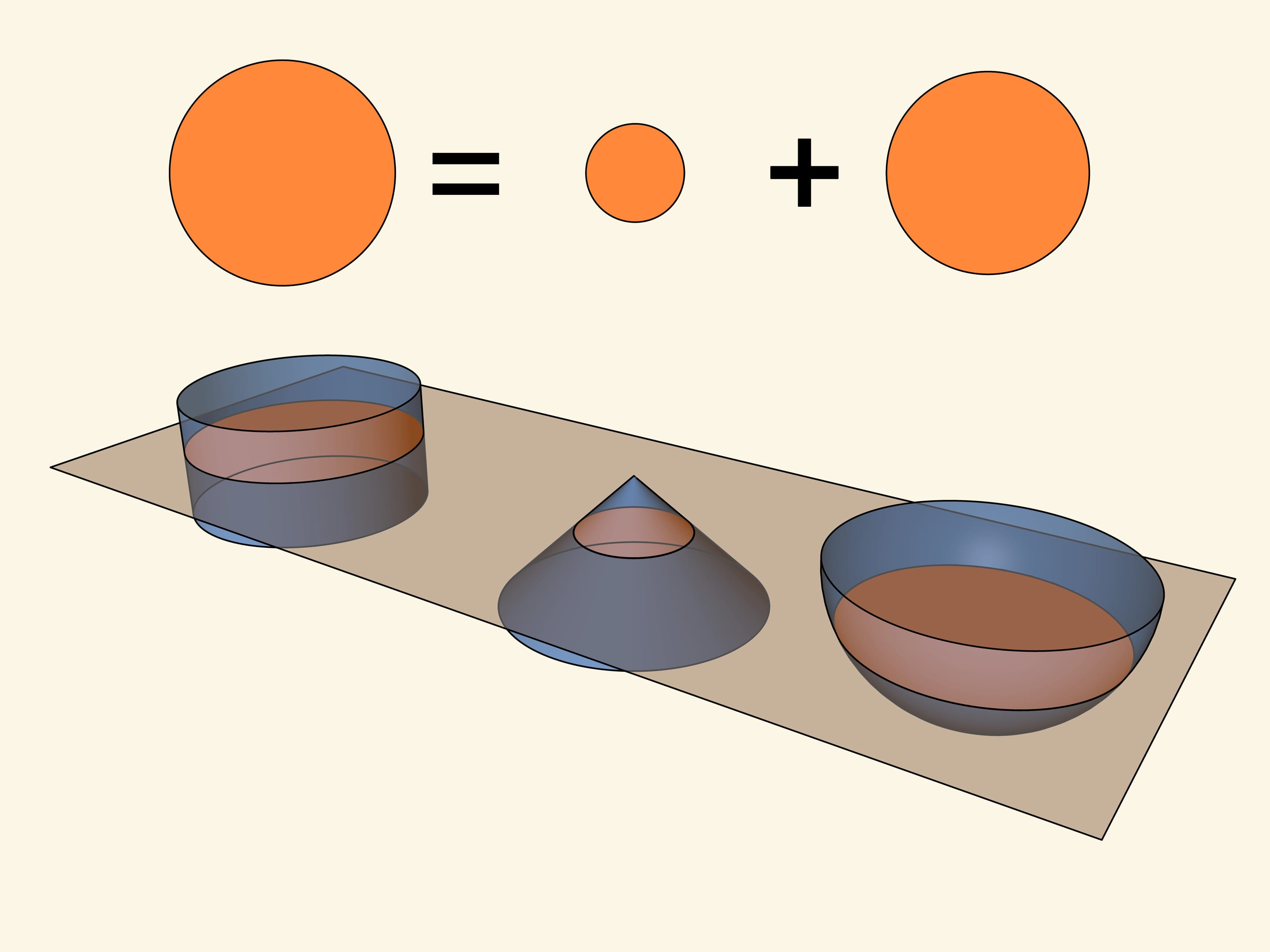
Let’s look at unbalanced scales. Imagine that there is a cylinder on the one side of the scales, with a height equal to a base radius, and there is a cone and a half of a sphere on the other side of the scales, at the same distance from a pendulum as a cylinder. So a radius of a cone base and a height are equal to the radius of a cylinder, radius of a ball is equal to radius of a cylinder.
Let’s start to collect these figures by layers, so that heights of layers of each of three figures are equal. It turns out that in сase of mentioned relations unbalanced scales will always come to balance. When figures are fully collected, scales will be in balance. Consequently, volume of a cylinder is equal to a sum of volumes of a cone and a half of a sphere, if radiuses and heights of all three figures are equal.
It is surprising: on the one side of a scale there is a simple figure — a straight circular cylinder, and on the other side there is also one of relatively simple figures — a straight circular cone, and a figure, which balances the scales is a sphere.
The case is that if we draw a plane, which is parallel to bases of figures, a square of a circle, which is received in a section of a cylinder, is equal to a sum of squares of circles, which are received in a section of the given cone and sphere. It is not difficult (in our times!) to check by a direct calculation, that equality of squares will be true for any position of a сutting plane.
Equality of volumes leads from the mentioned equality of squares, like it is told now, according to the principle of Cavalieri (it. Bonaventura Francesco Cavalieri, lat. Cavalerius, 1598—1647).
Relation of volumes of a cylinder and a cone was known before Archimedes:
Having, however, now discovered that the properties are true of these figures, I cannot feel any hesitation setting them side by side both with my former investigations and with those of the theorems of Eudoxus <Eudoxus Сnidus, ancient Greek Εὔδοξος, lat. Eudoxus, c. 408 BC — c. 355 BC> on solids which are held to be most irrefragably established, namely, that any pyramid is one third part of the prism which has the same base with the pyramid and equal height, and that any cone is one third part of the cylinder which has the same base with the cone and equal height.
Archimedes. On the sphere and cylinder.
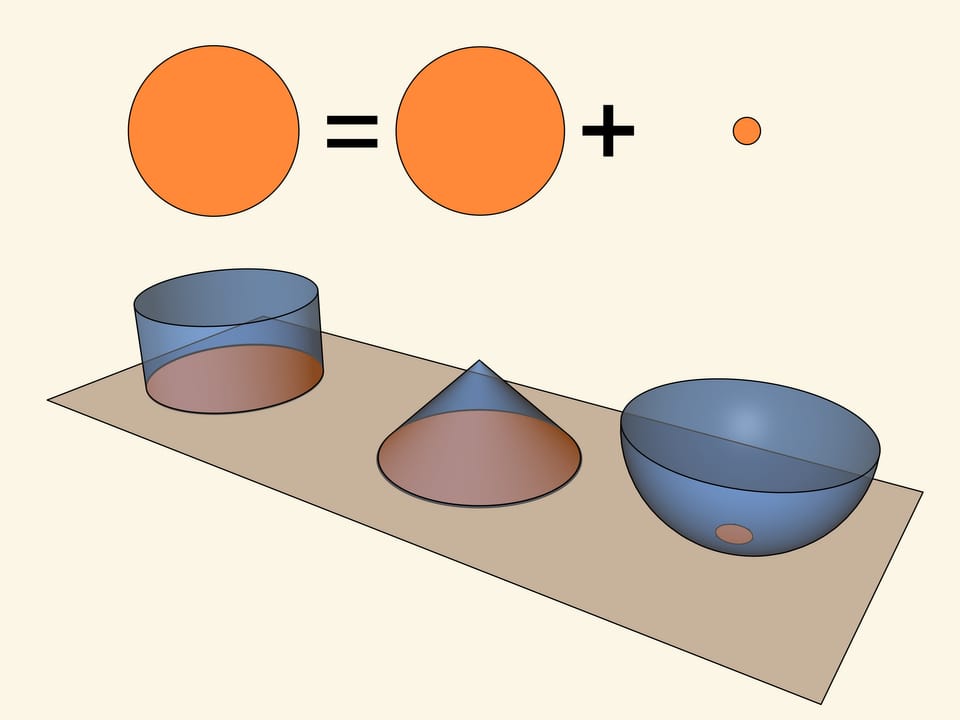
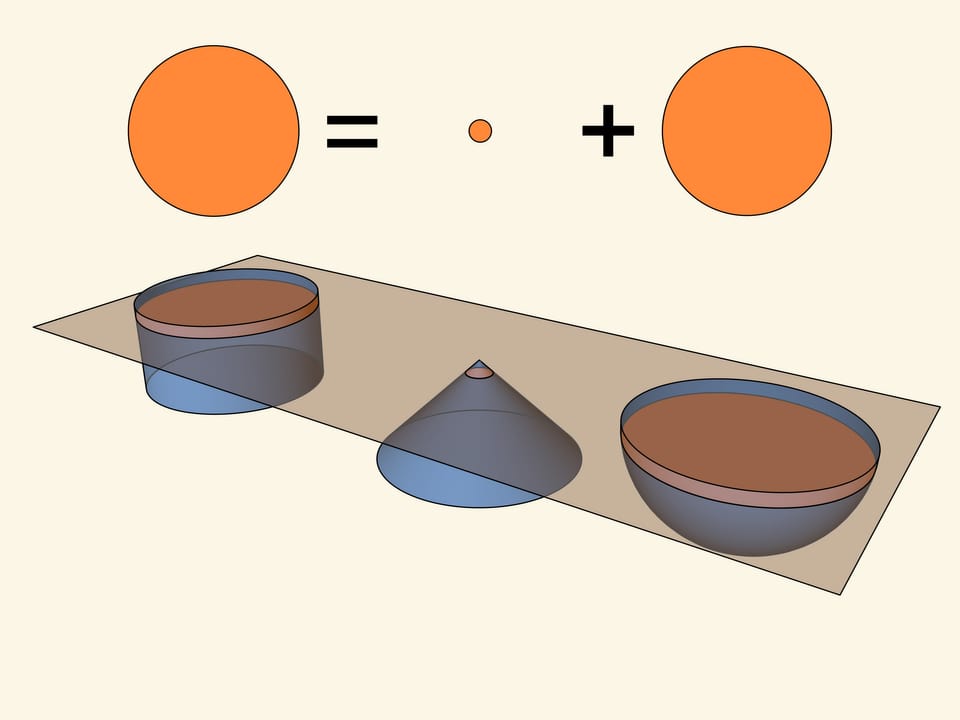
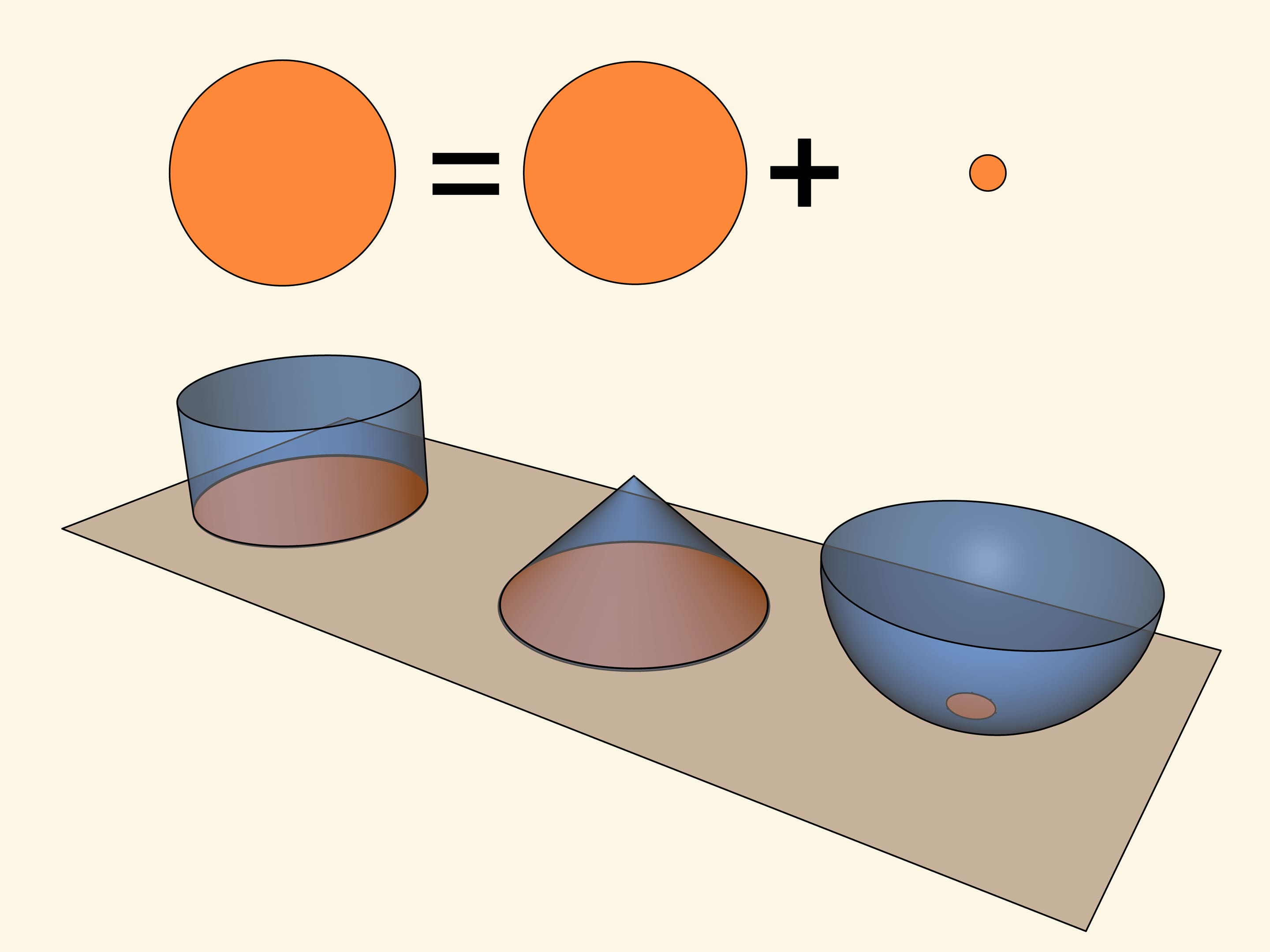
Balance of scales enables to express the volume of a half of a sphere through a volume of a cylinder. Deducing one third from volume of a cylinder — a volume of a cone with the same base and height, one receives that volume of a half of a ball is equal to $2/3$ of a cylinder’s volume.
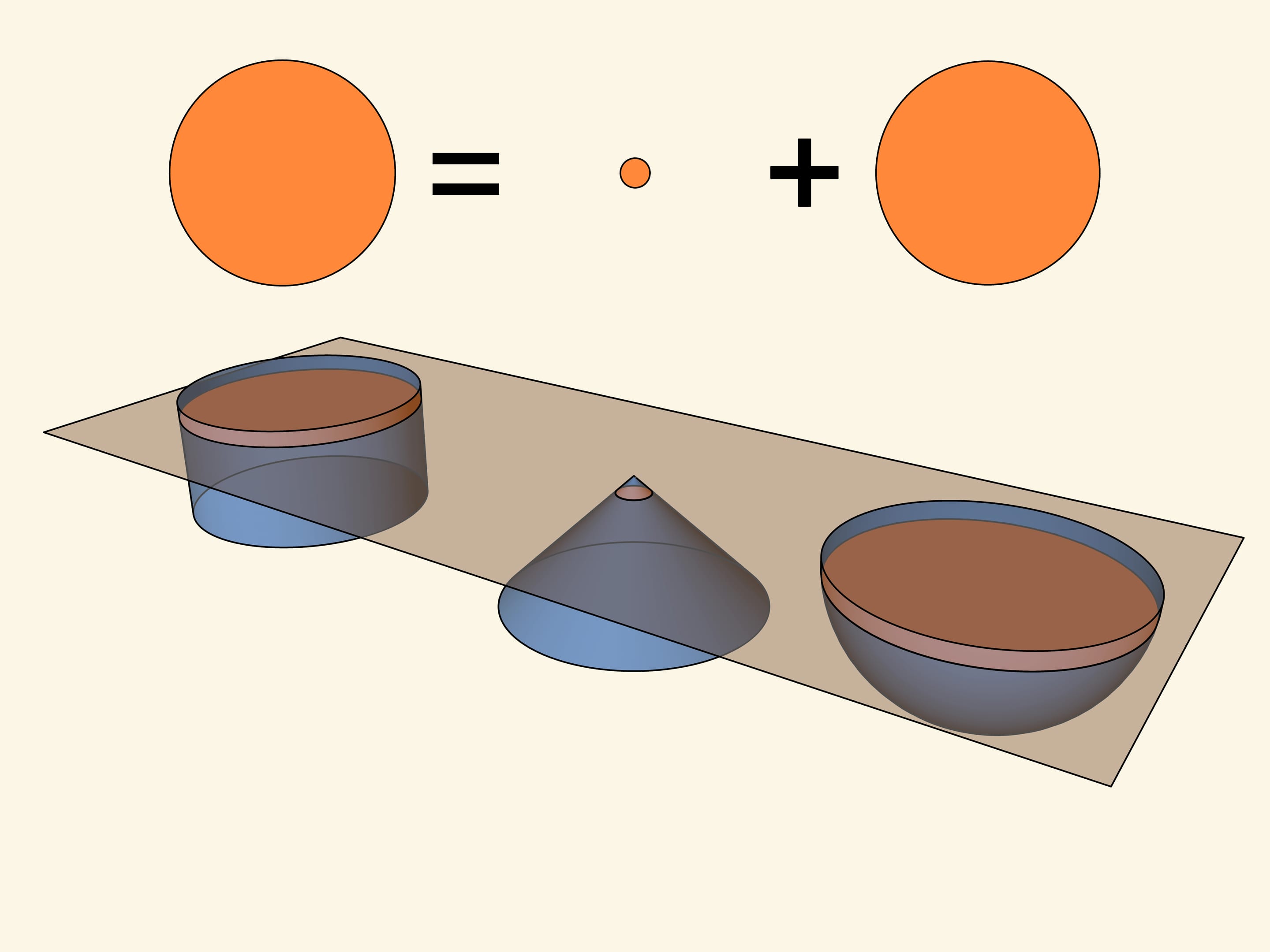
Тем Consequently, a relation, described by Archimedes, has been proved: a volume of a ball is equal to a volume of a cylinder, circumscribed around the sphere. It is interesting that, as Archimedes has settled, squares of their surfaces are in the same relations.
From Archimedes’ correspondence one can determine a clear formula for a sphere’s volume. In case of a cylinder, circumscribed around a sphere with a radius $R$, a square of its basis is equal to $\pi R^2$, and its height is equal to $2R$. Consequently, volume of a cylinder is equal to: $(\pi R^2)\cdot (2 R)=2 \pi R^3$. Multiplying on a coefficient $2/3$, one will receive a formula for a volume of a sphere: $4/3 \cdot \pi R^3$
Now, however, it will be open to those who possess the requisite ability to examine these discoveries of mine. They ought to have been published while Conon was still alive <Сonon Samian, ancient Greek Κόνων, Latin Conon, c. 280 BC — c. 220 BC>, for I should conceive that he would best have been able to grasp them and to pronounce upon them the appropriate verdict; but, as I judge it well to communicate them to those who are conversant with mathematics, I send them to you with the proofs written out, which it will be open to mathematicians to examine.
Archimedes. On the sphere and cylinder.