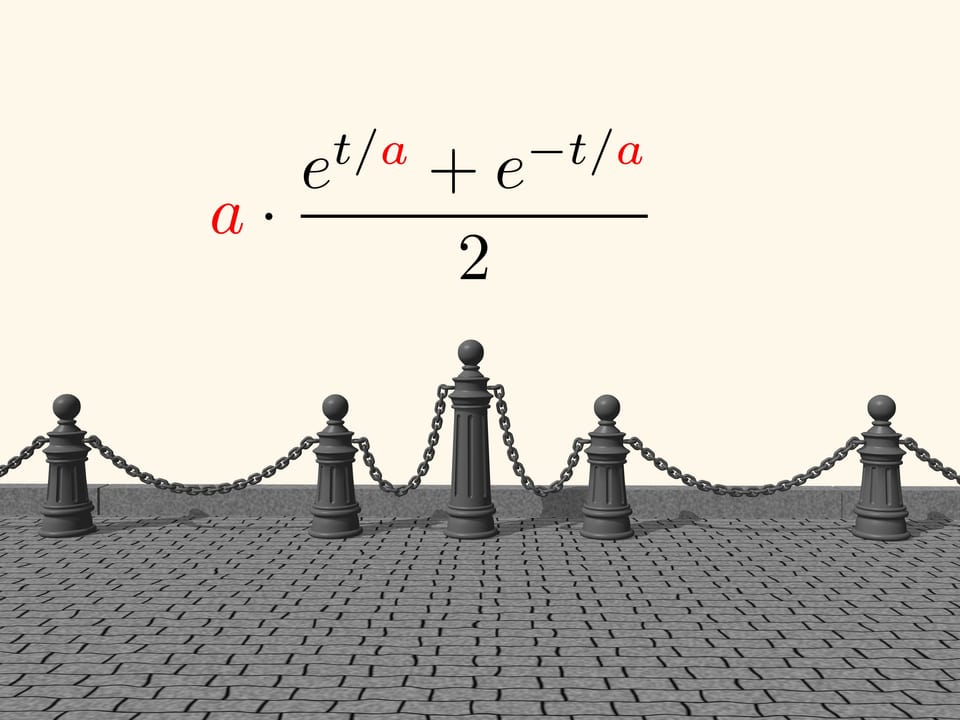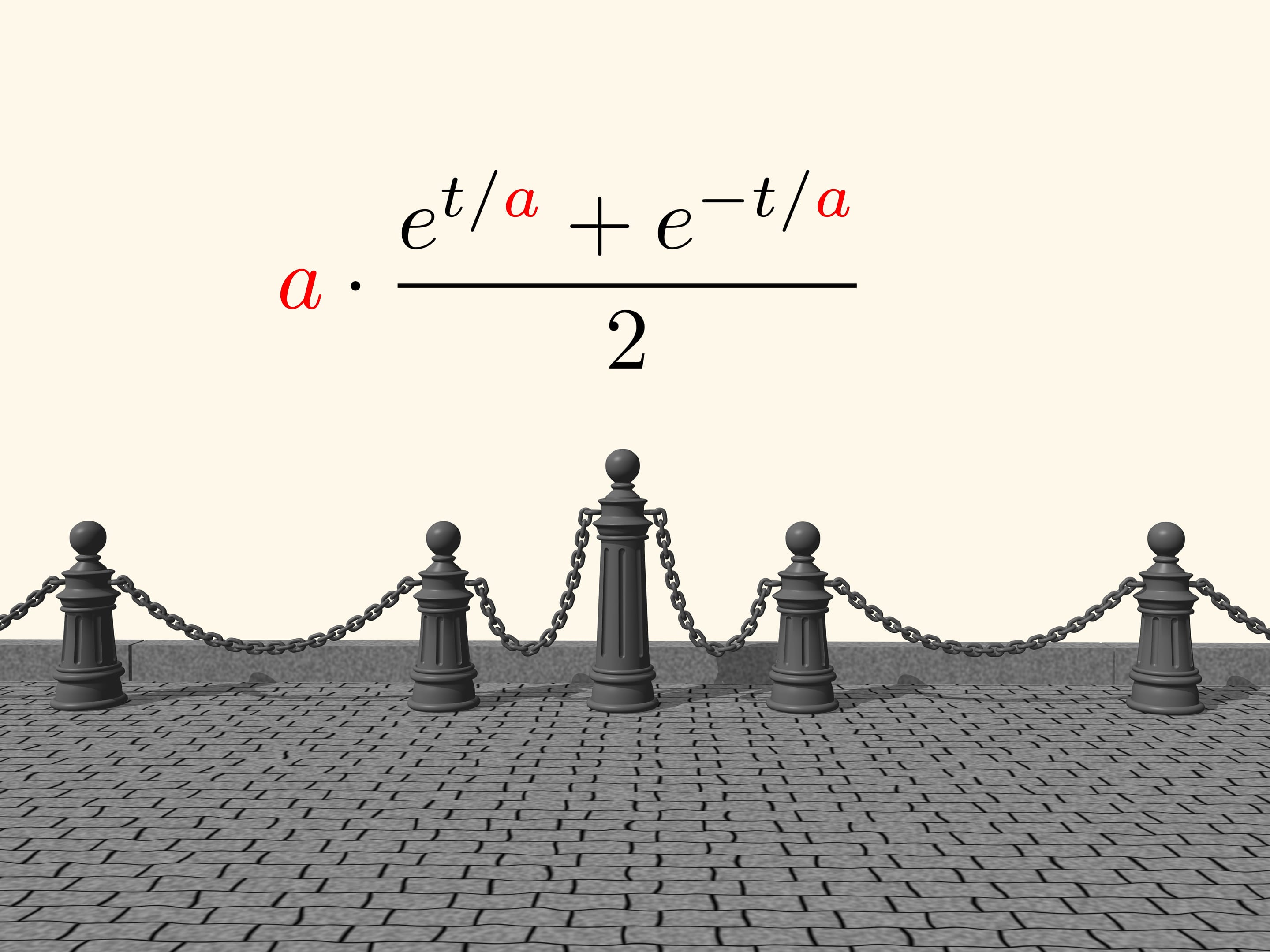... Another way to trace the searched parabola on a wall is as follows. Let us plant two nails in the wall at the same height above the horizon at a distance from each other, which is double the width of the rectangle, where we want to inscribe the parabola. Hang to the nails the ends of a thin chain of a length such that its lowest point is at a distance from the level of the nails equal to the height of the rectangle. The hung chain takes the form of a parabola, so that, marking the points on the wall through the links in the chain, we obtain the trace of a parable, which is bisected by the perpendicular line segment that passes between the two nails in its midpoint.
Galileo Galilei “Conversations and mathematical proofs.” 1638.
But the scientist was wrong. Between the parabola and the line drawn by means of the hung chain there is a small difference. Just half a century after John Bernoulli, Christiaan Huygens and Gottfried Leibniz found the equation of the “catenary”. In it a parameter appears, whose change allows to get different curves, corresponding to chains more or less stretched between two points. The name “catenary” was invented by Huygens.
Along this line not only runs a chain hanging, but any smooth rope, suspended between two points, subject to gravity. You might look at this line, for example, visiting a museum.
But now let us turn our picture upside down.
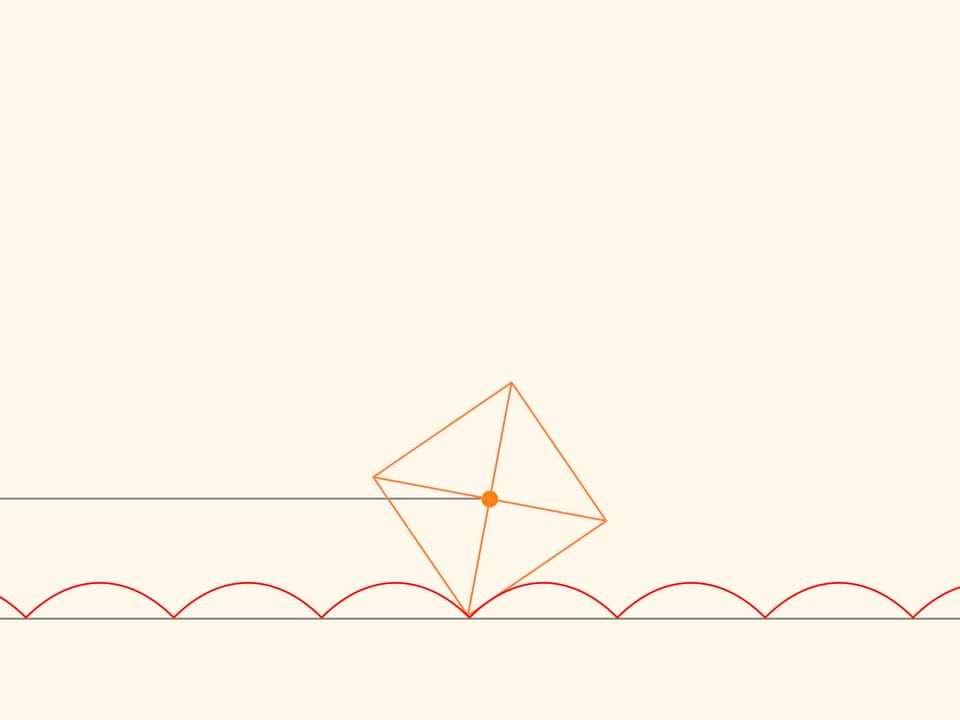
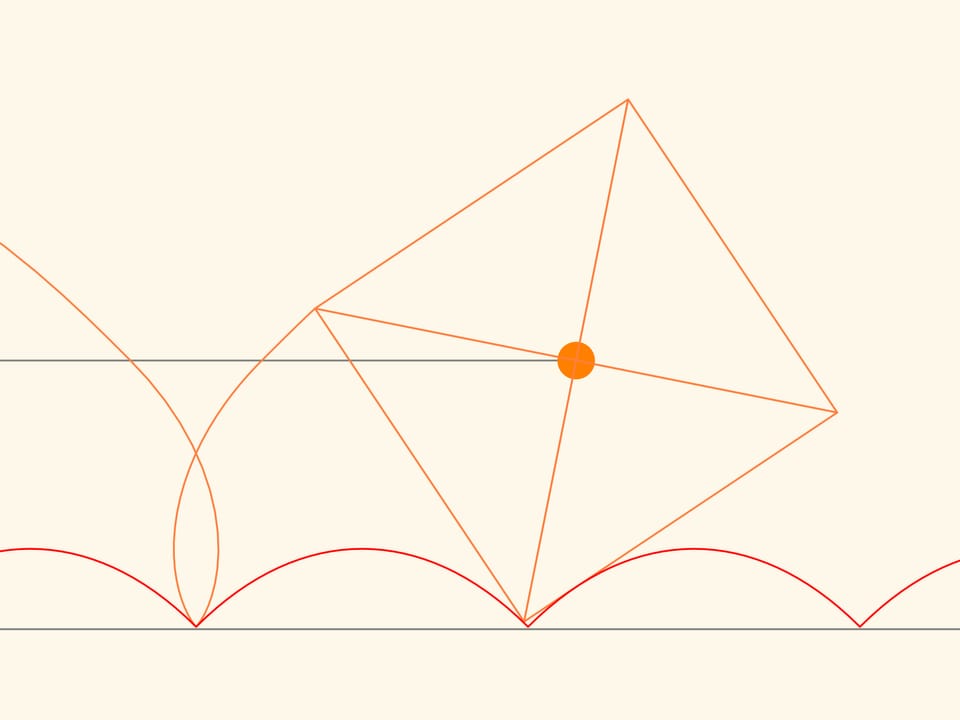
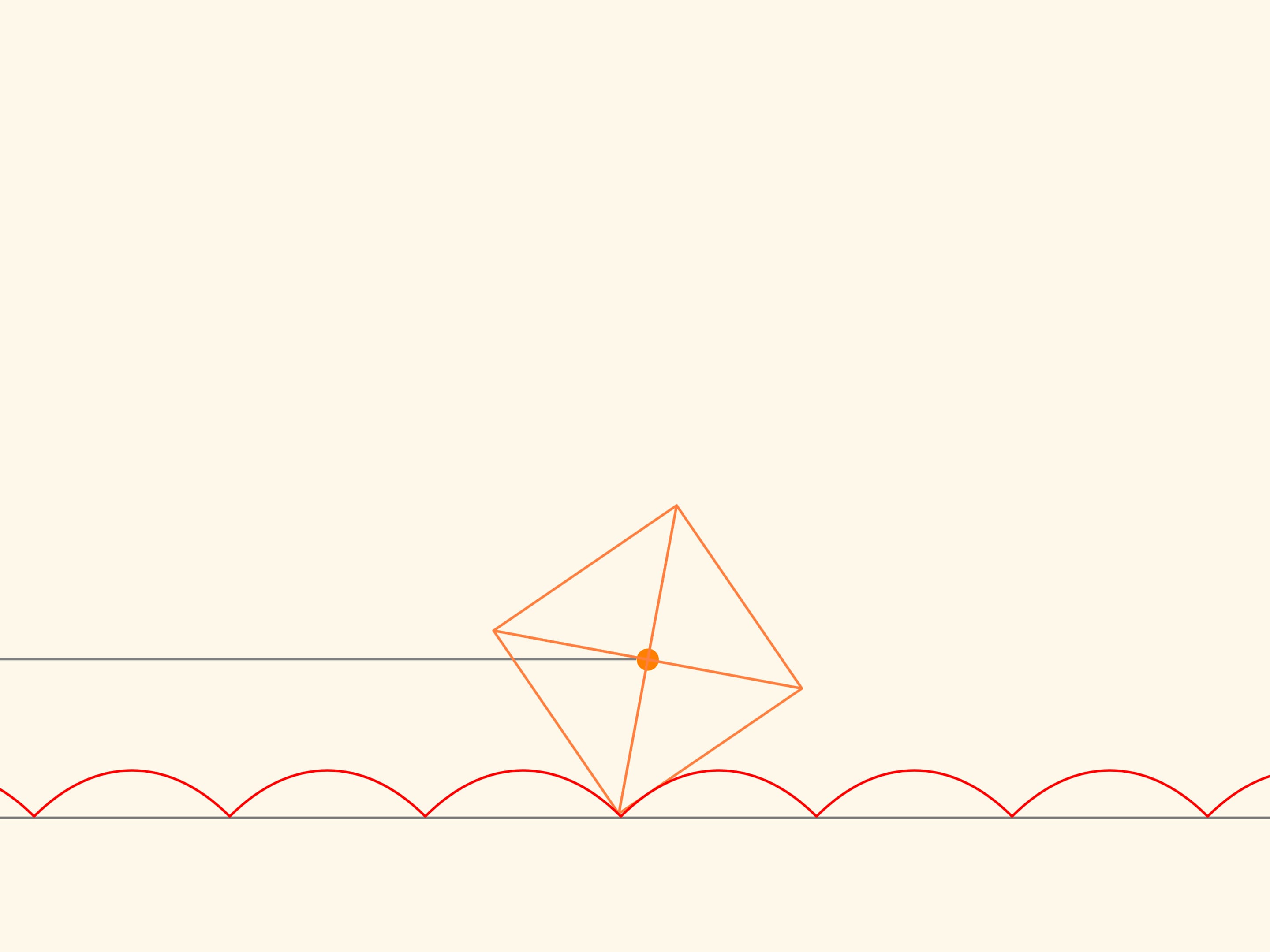
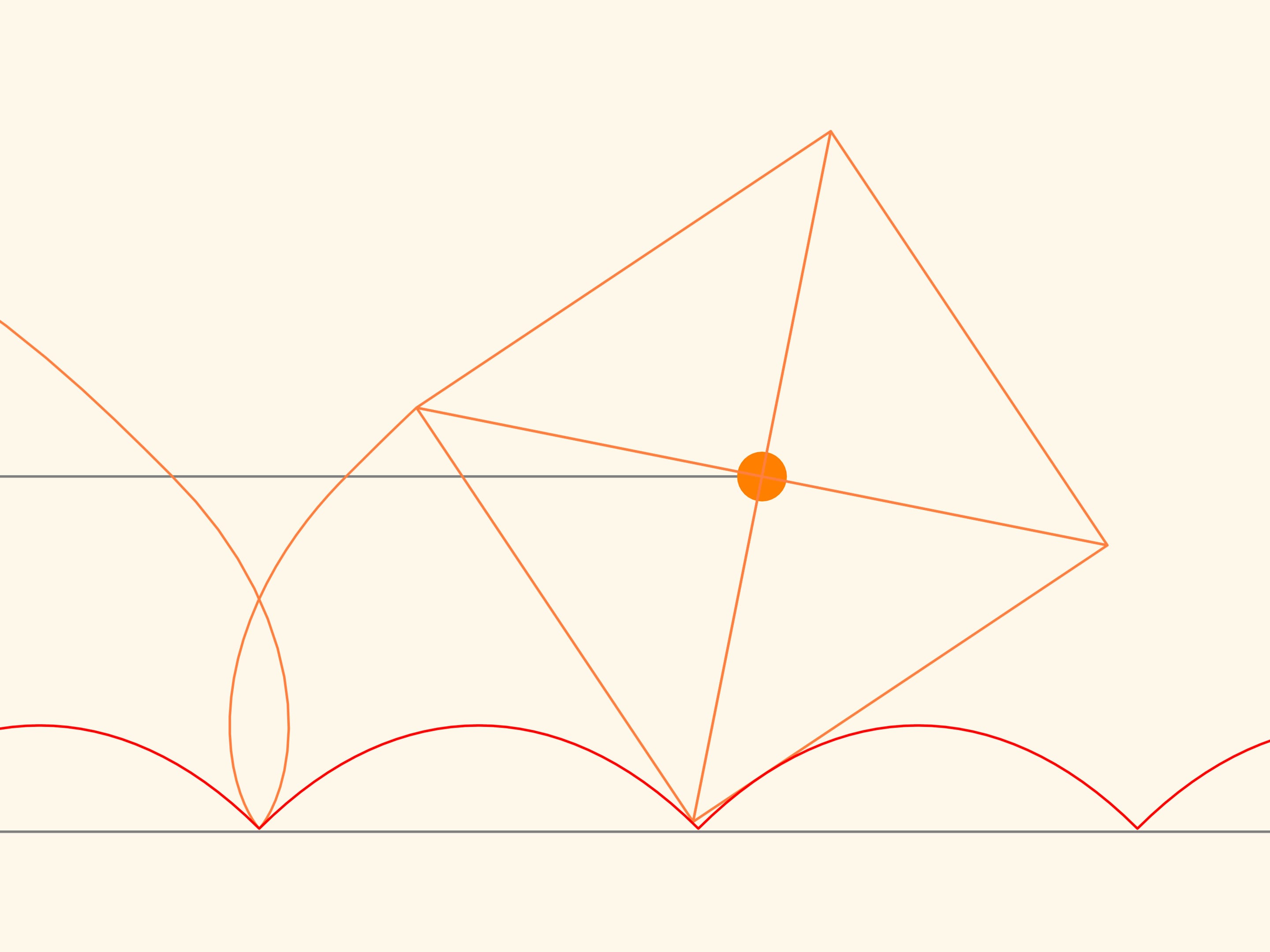
If we select a special value of the parameter in the equation, then the centre of the square, which runs without slithering along the arc of a catenary, will move along a straight line!
We trace the trajectory of one of the corners of the square. This curve never crosses the line and, therefore, a cart that moves on square wheels can exist! In addition, the distance between the axles of the cart is not necessarily a multiple of the length of a bump of the catenary line, since the wheels may be in different phases of rotation.
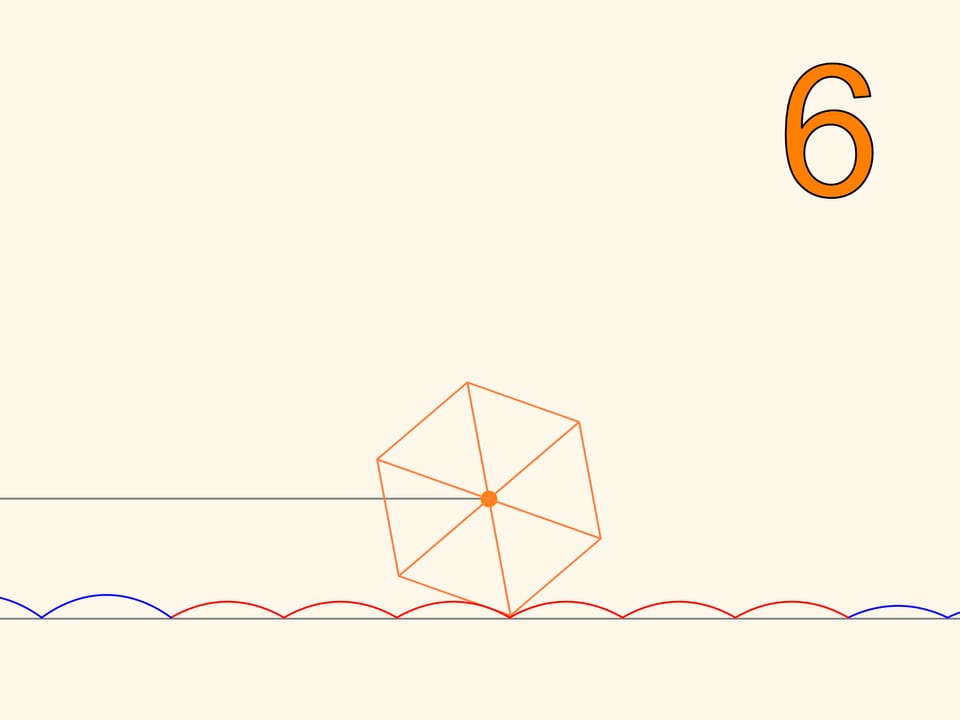
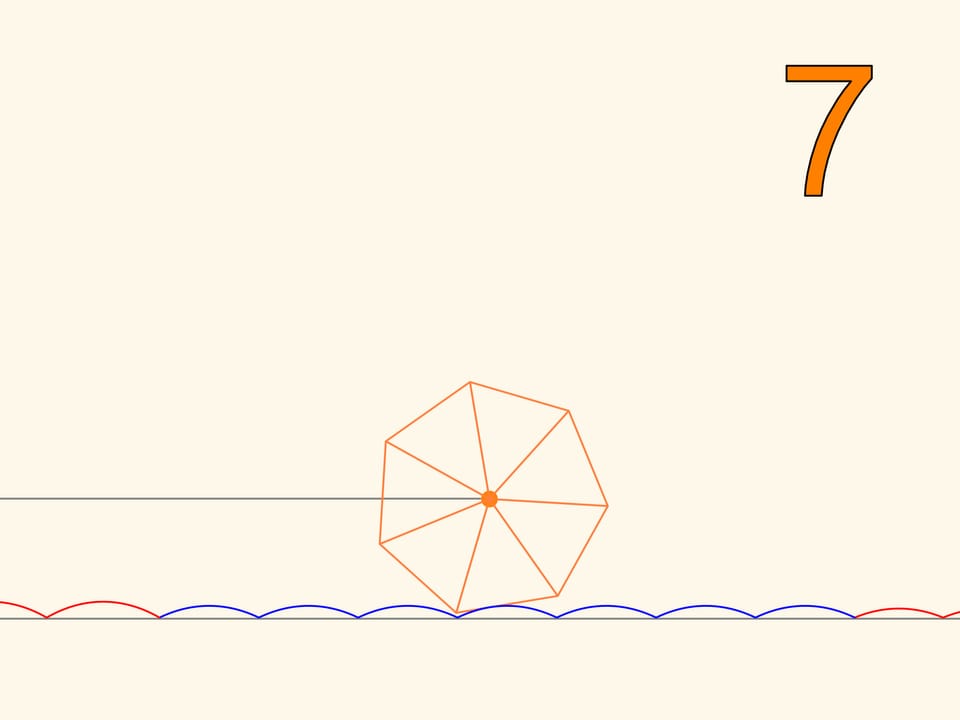
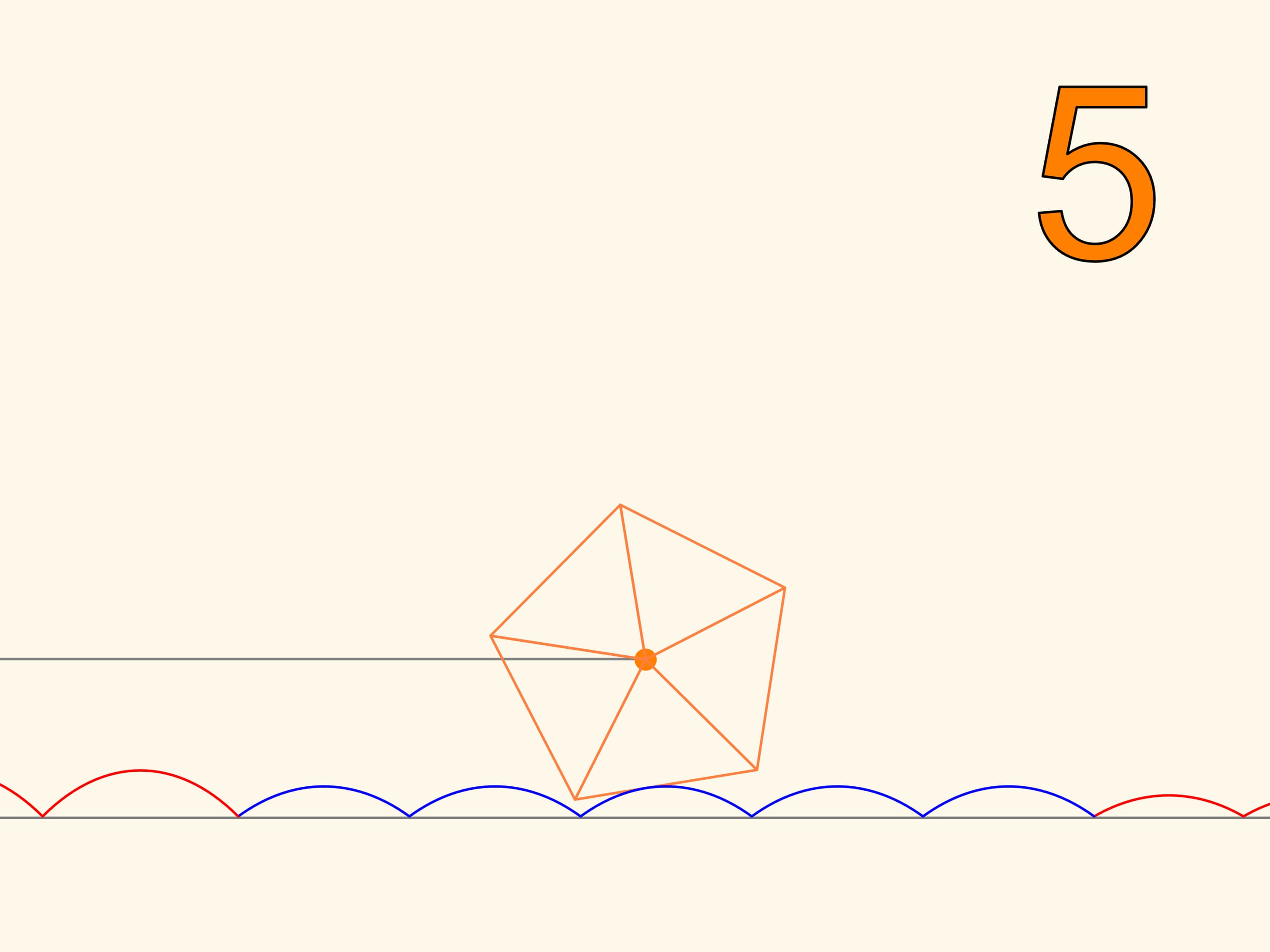
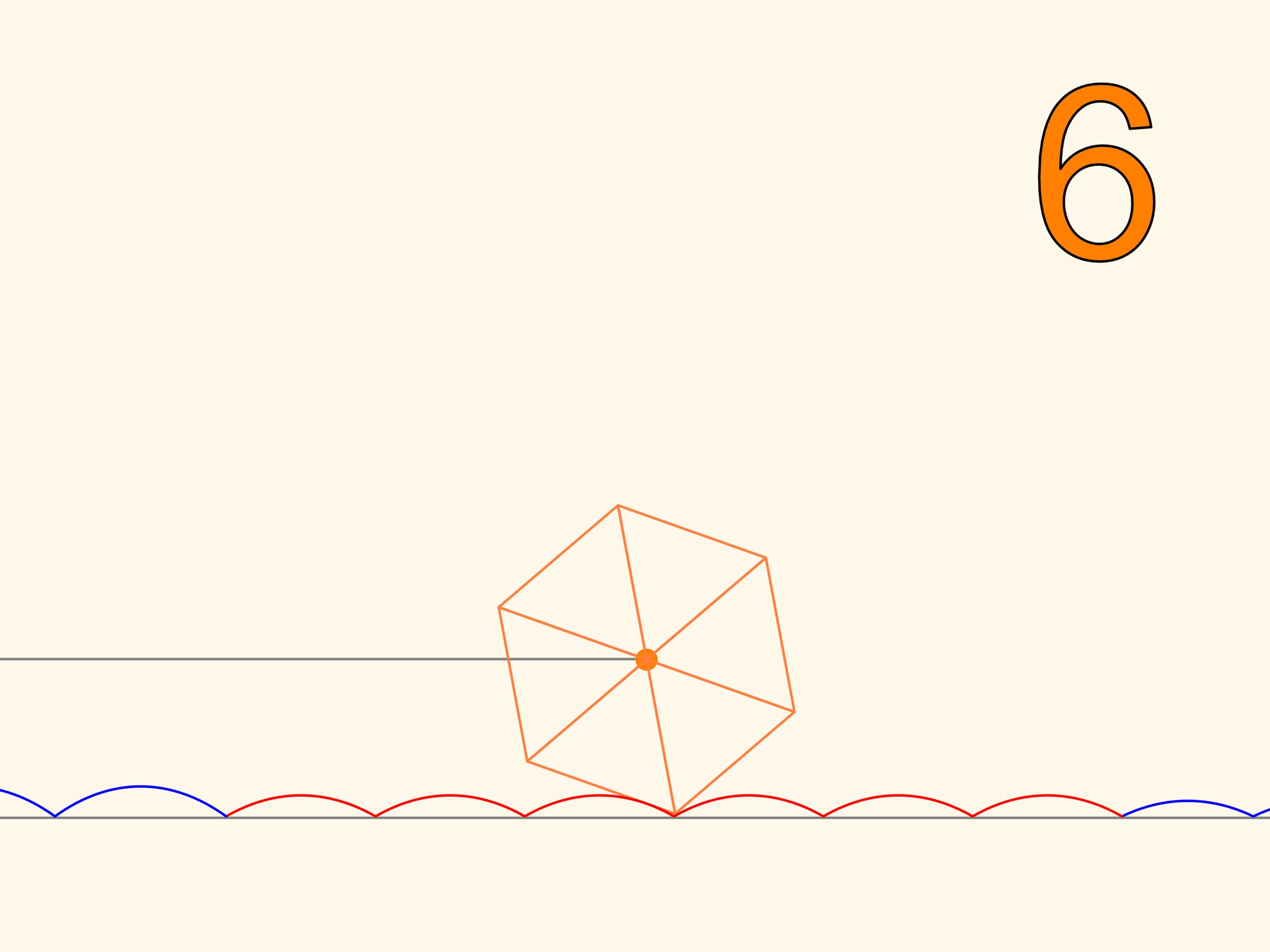
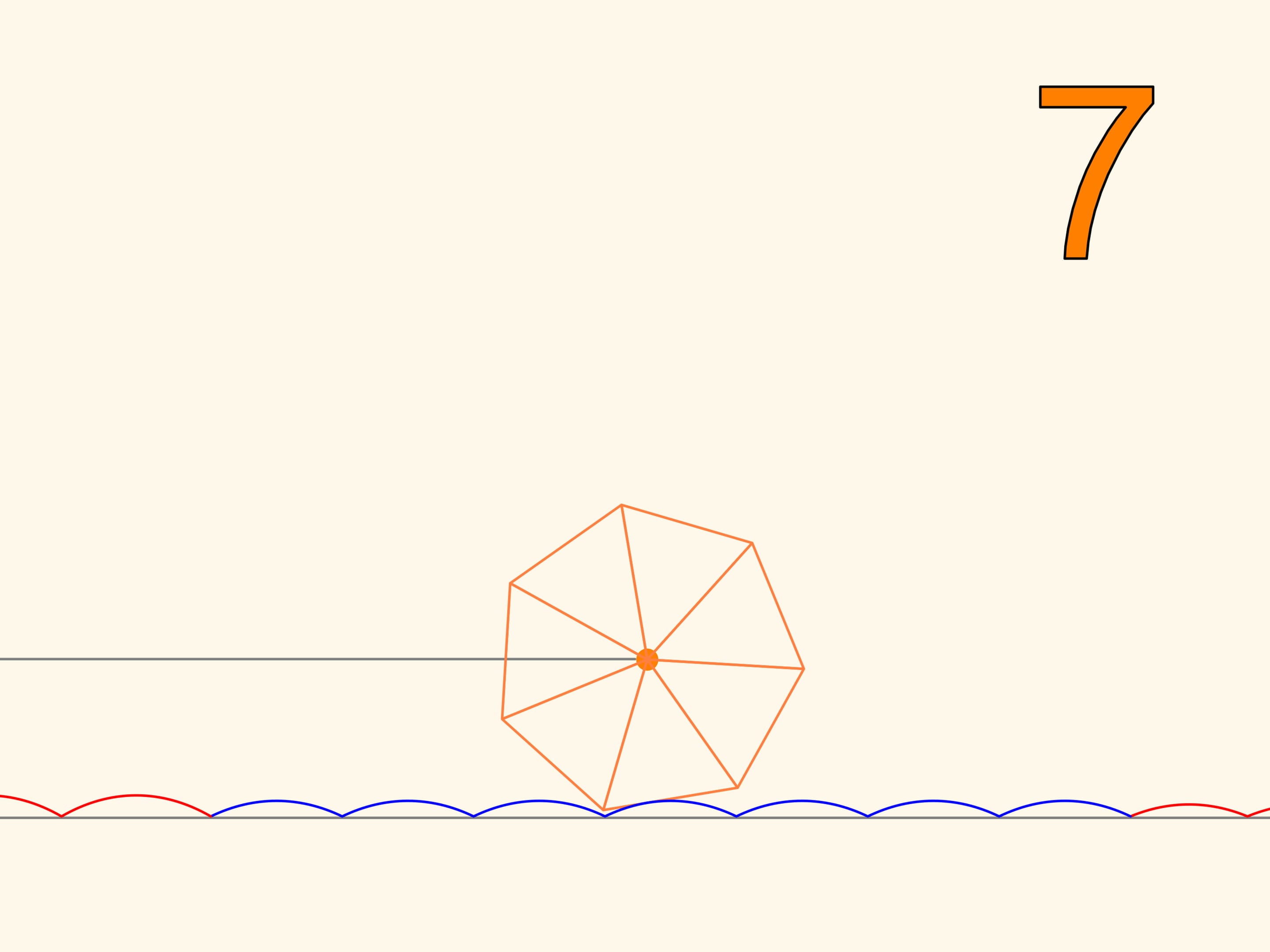
So we have learned to move on square wheels. But we will find that we can also go on wheels that have the shape of any regular polygon. Only, the road cannot be flat, but it will take the form of a series of catenaries, with the value of the parameter chosen according to the number of polygon’s sides. The more the polygon, increasing the number of sides, approaches a circle, the more the corresponding value of the parameter decreases, and the more the stretch of road, needed to make a full turn of the wheel approaches a segment with the length of the circle. This is the evolution of the wheel, which, unlike the regular polygons, which can only roll on a catenary, may be rolled on a plane and can change direction.
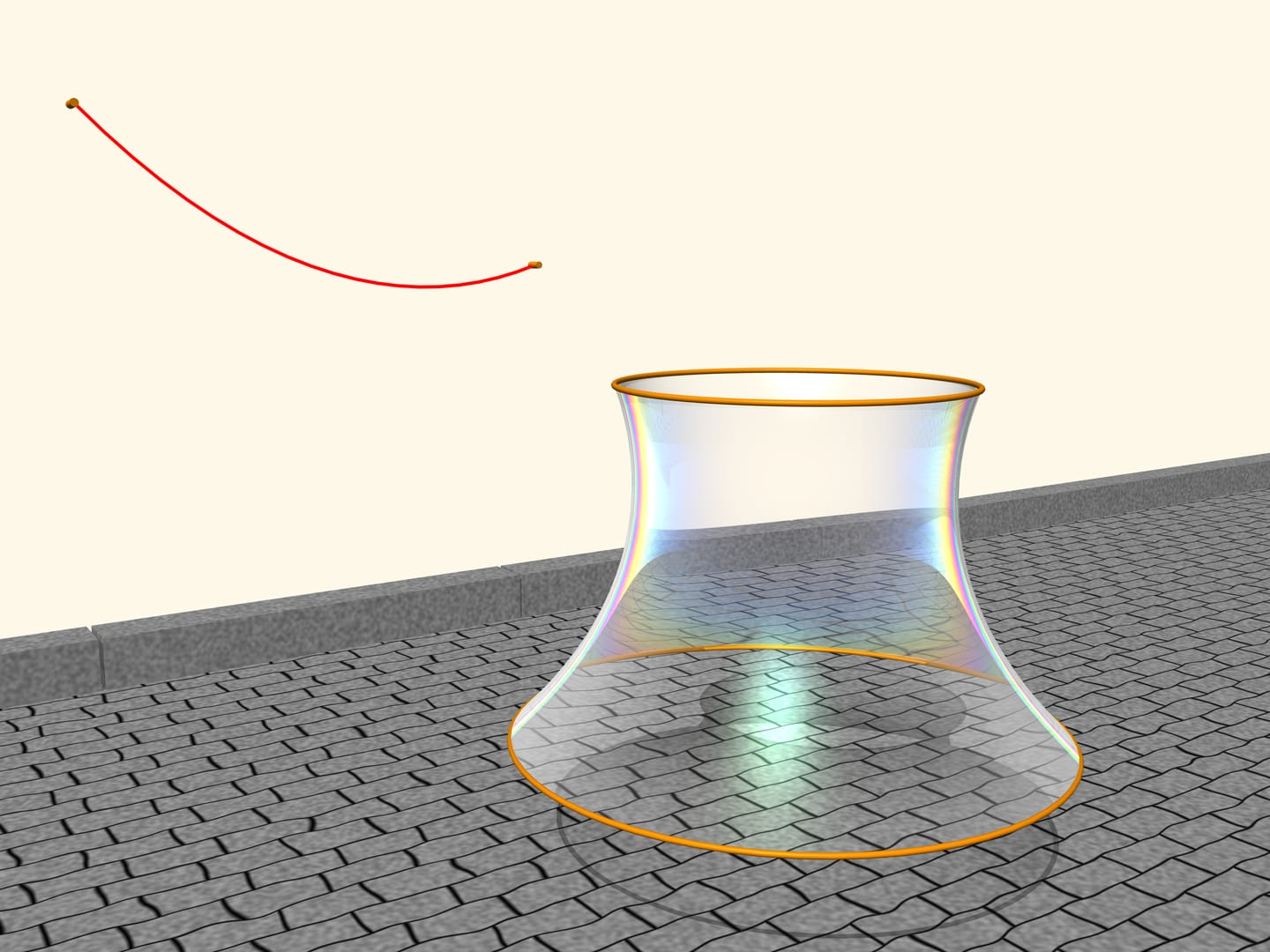
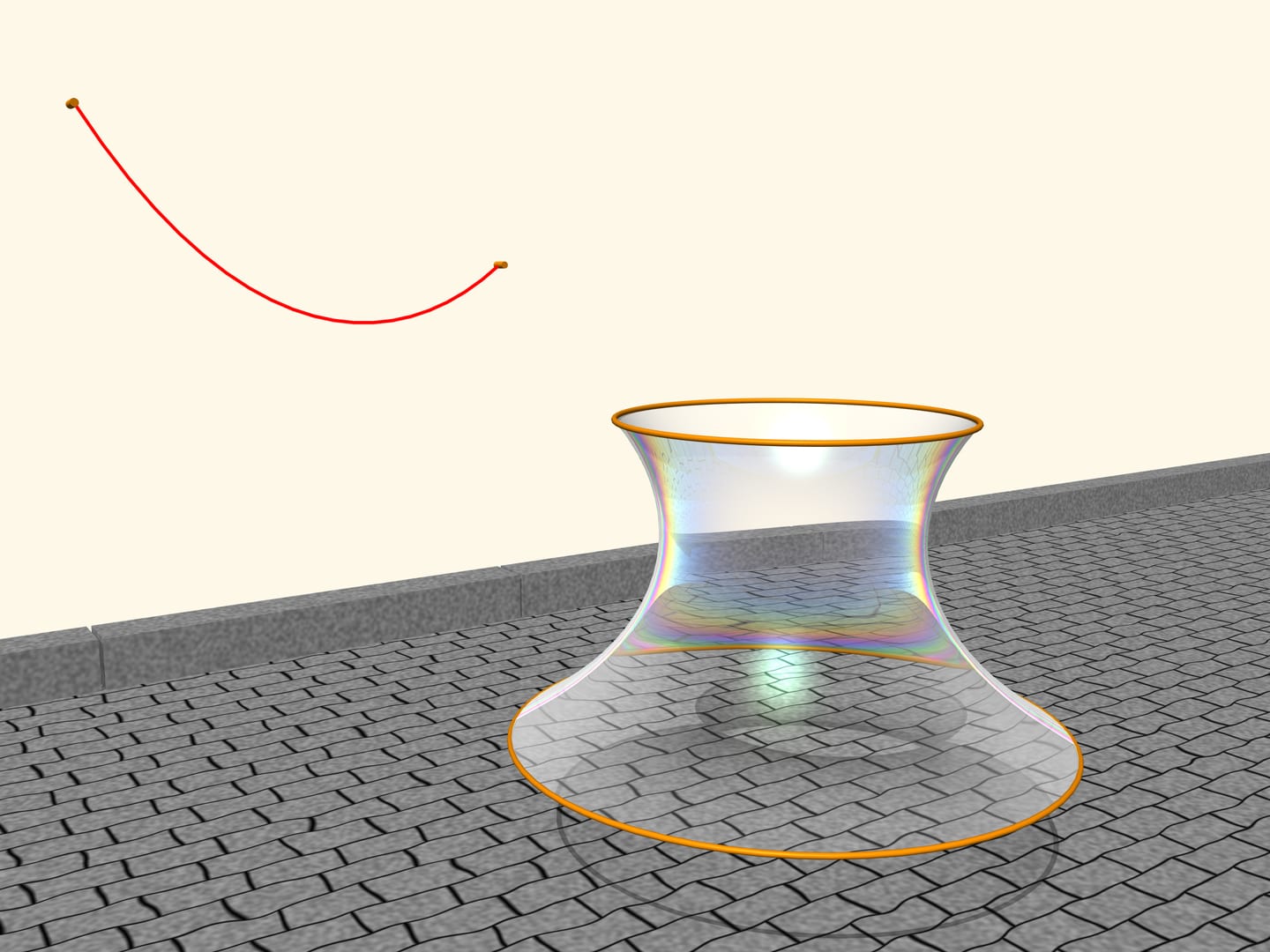
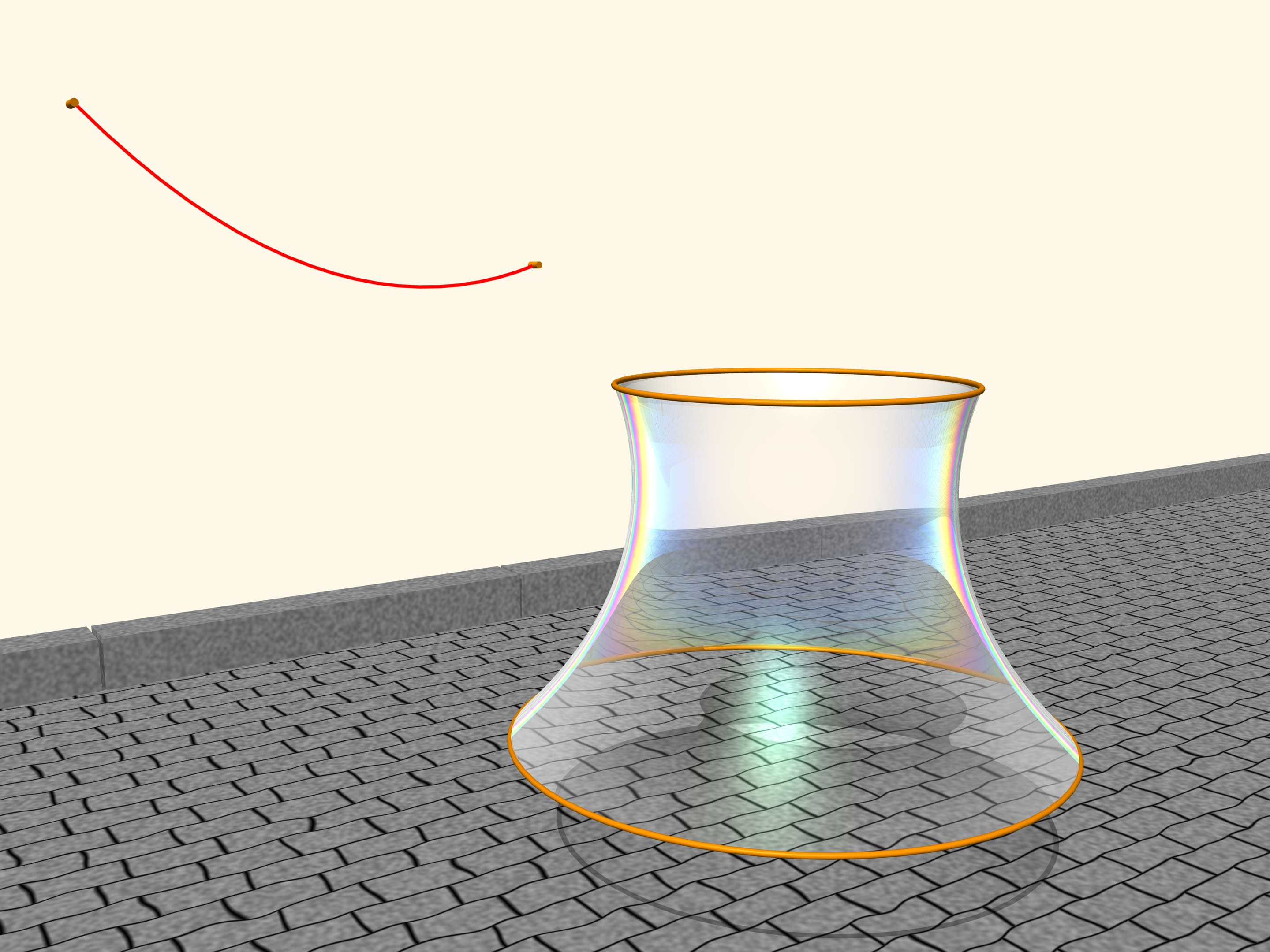
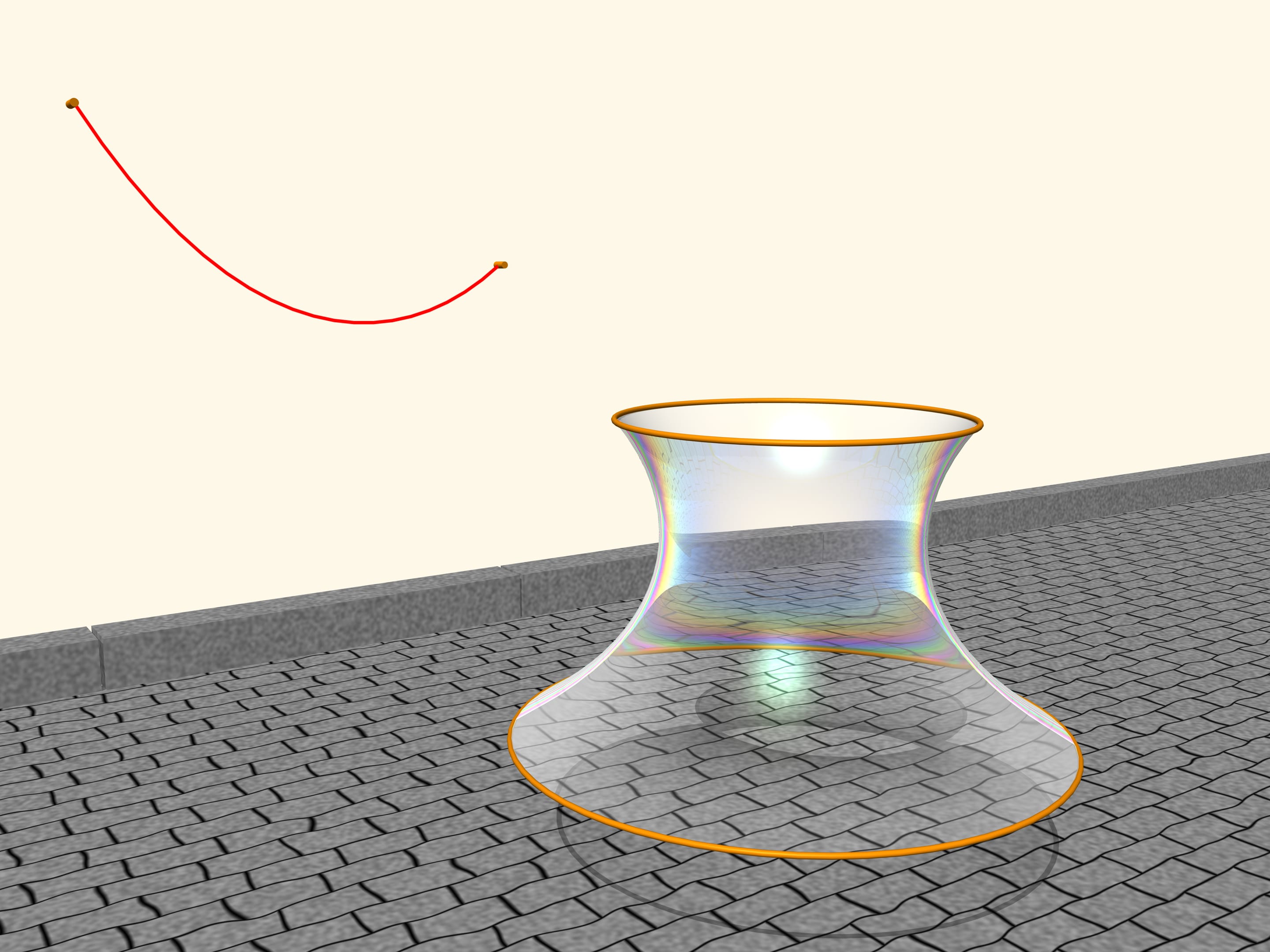
Observe a soap film between two circles, placed on two parallel planes. The soap film is an extraordinary object: it is extremely light, so that its internal forces are much stronger than gravity, and by consequence the film always takes the form of a surface that has the minimum area among all surfaces with the same boundary conditions.
Which shape the film, suspended between the two circles, will take? It turns out that it will take the form of a surface obtained by rotating a catenary! If we change the distance between the levels where the circles are located, also the surface will change, but its profile will always be that of a catenary of a fixed length, suspended from two poles of corresponding height placed at the corresponding distance. All this was proved by Leonhard Euler in the work “Method to find curved lines with properties of maximum or minimum” of 1744. He called this surface catenoid (from the Latin catena, chain, and the Greek eidos, appearance).