Invisible body ⁠

Herbert Wells went three times in Russia. During his second visit — then there was already the Soviet Union — he met Yakov Isidorovich Perelman, who submitted to the atten­tion of the author of “The Invis­ible Man” the following fact: if a man is completely invis­ible, then the crys­talline lens of his eyes are invis­ible, and there­fore they do not refract the light and do not convey the images on the retina. For this man every­thing is invis­ible!

But are there invis­ible bodies, albeit inan­i­mate? In 2009, math­e­mati­cians have shown that there exists inan­i­mate invis­ible beings!

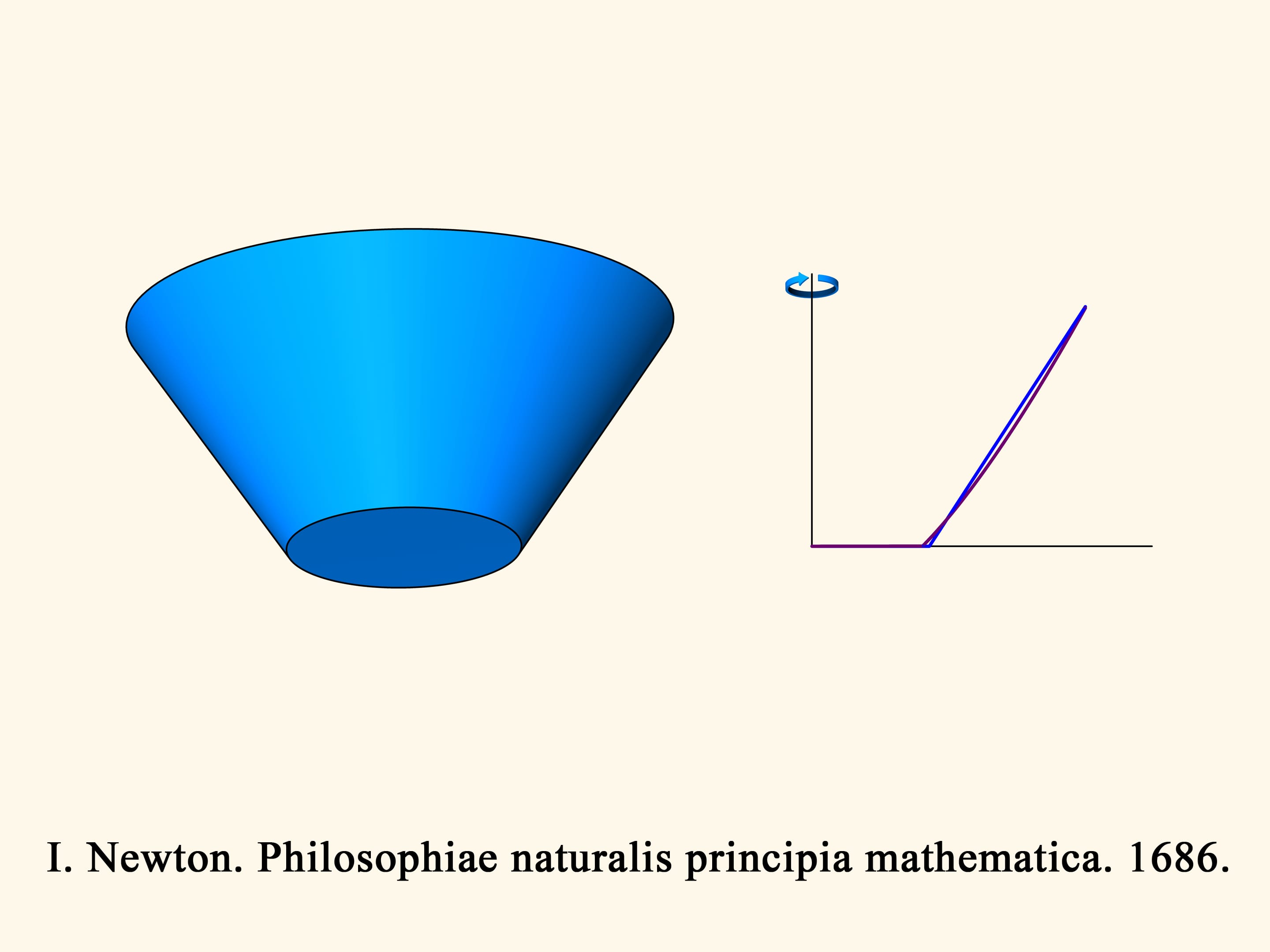
Let us start from the seven­teenth century. In “Math­e­mat­ical Prin­ci­ples of Natural Philos­ophy” (“Philosophiae Natu­ralis Prin­cipia Math­e­matica”) Isaac Newton studied the problem of the fall (or move­ment) of different bodies in a “rarefied medium, consisting of iden­tical parti­cles, arbi­trarily placed at equal distances from one another” that bounce elas­ti­cally when they collide with the bodies. Later this problem was called “Newton’s aero­dy­namic problem.”

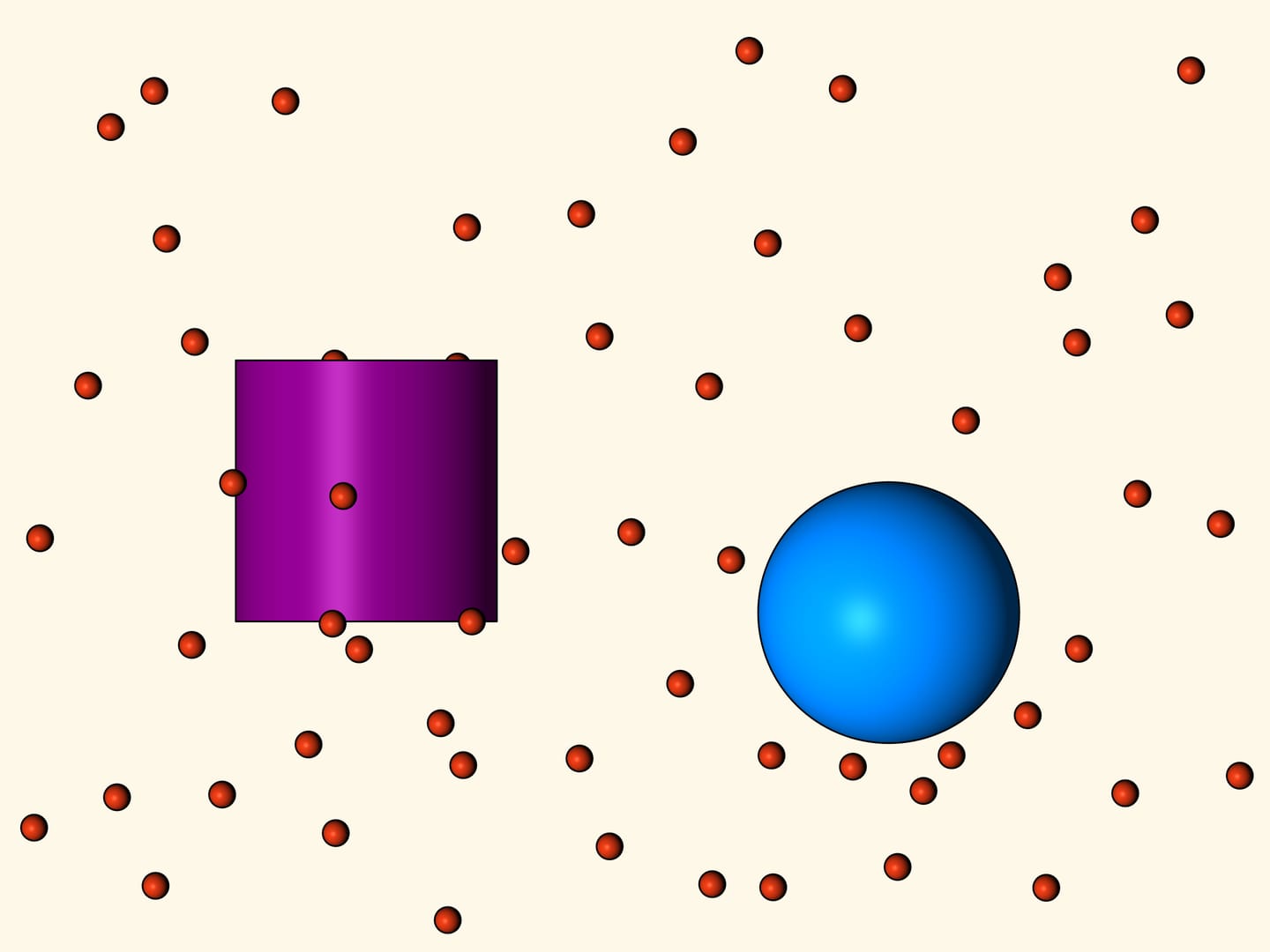
The first two bodies consid­ered are a sphere and a cylinder, both with the same diam­eter. Which of these bodies meet less resis­tance? Newton shows by geometric methods that the resis­tance for the sphere will be twice lower.

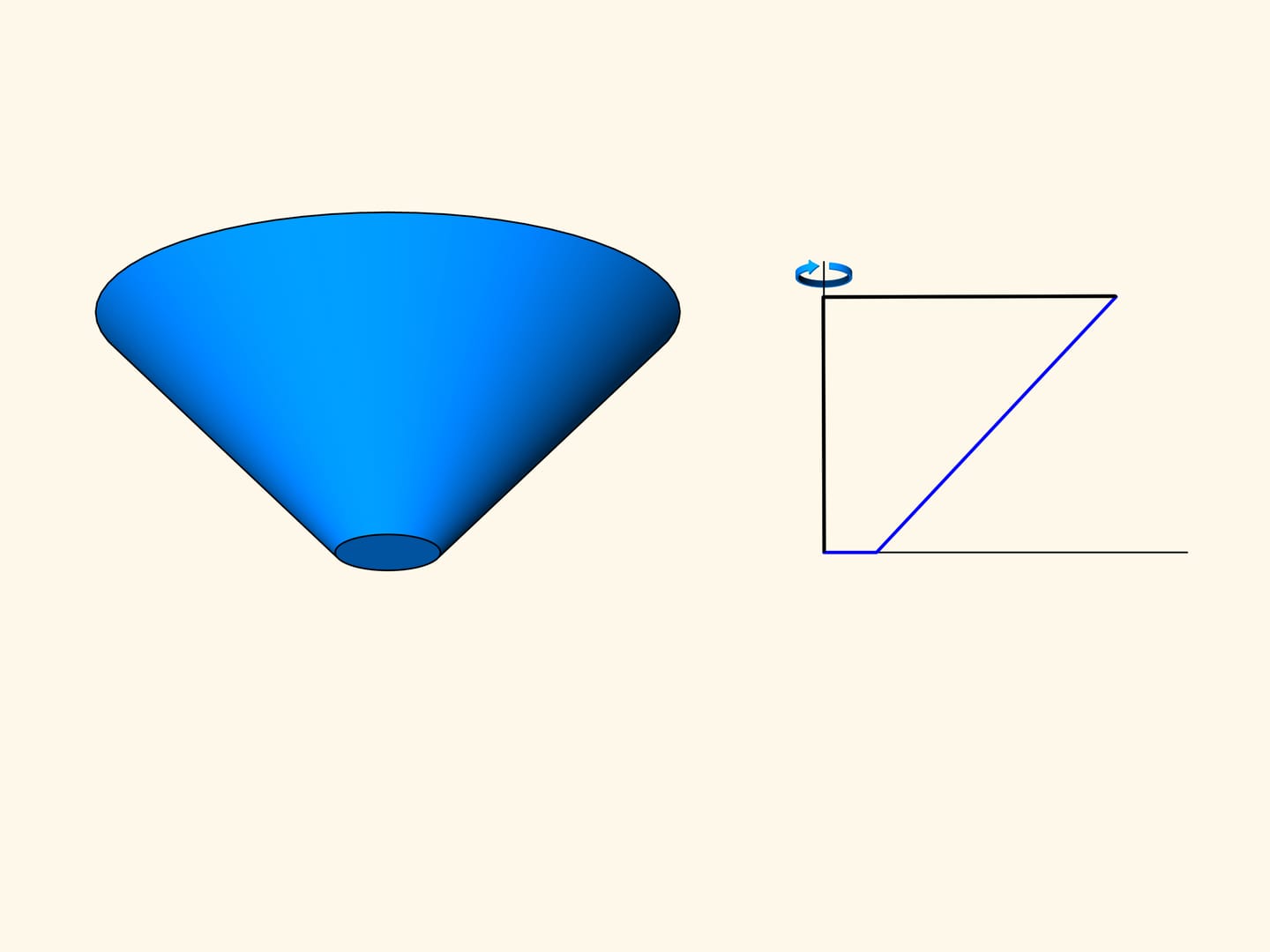
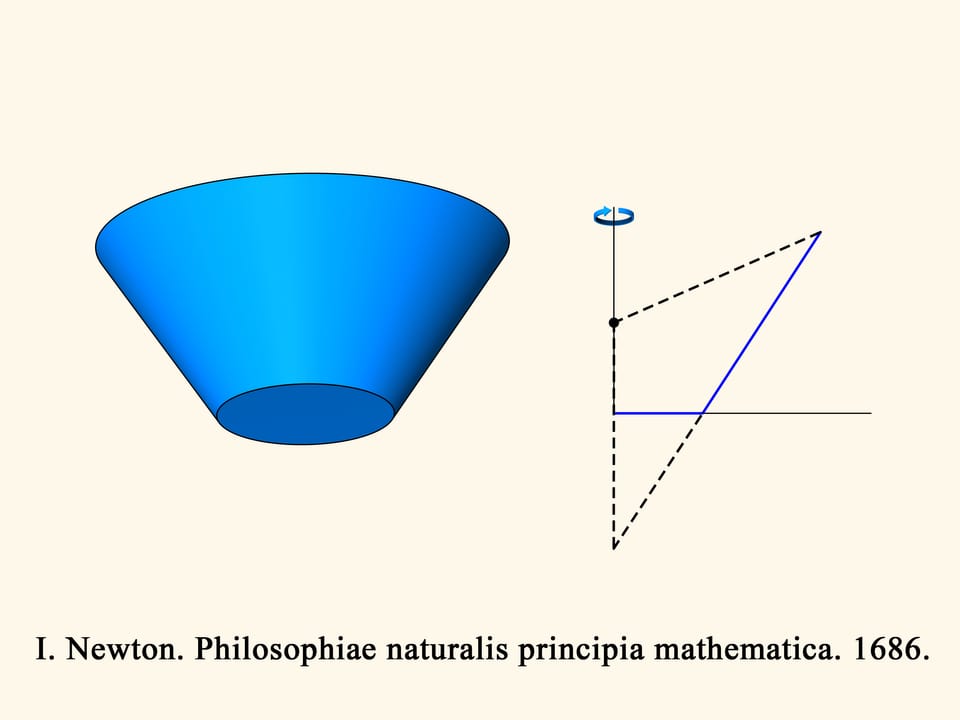
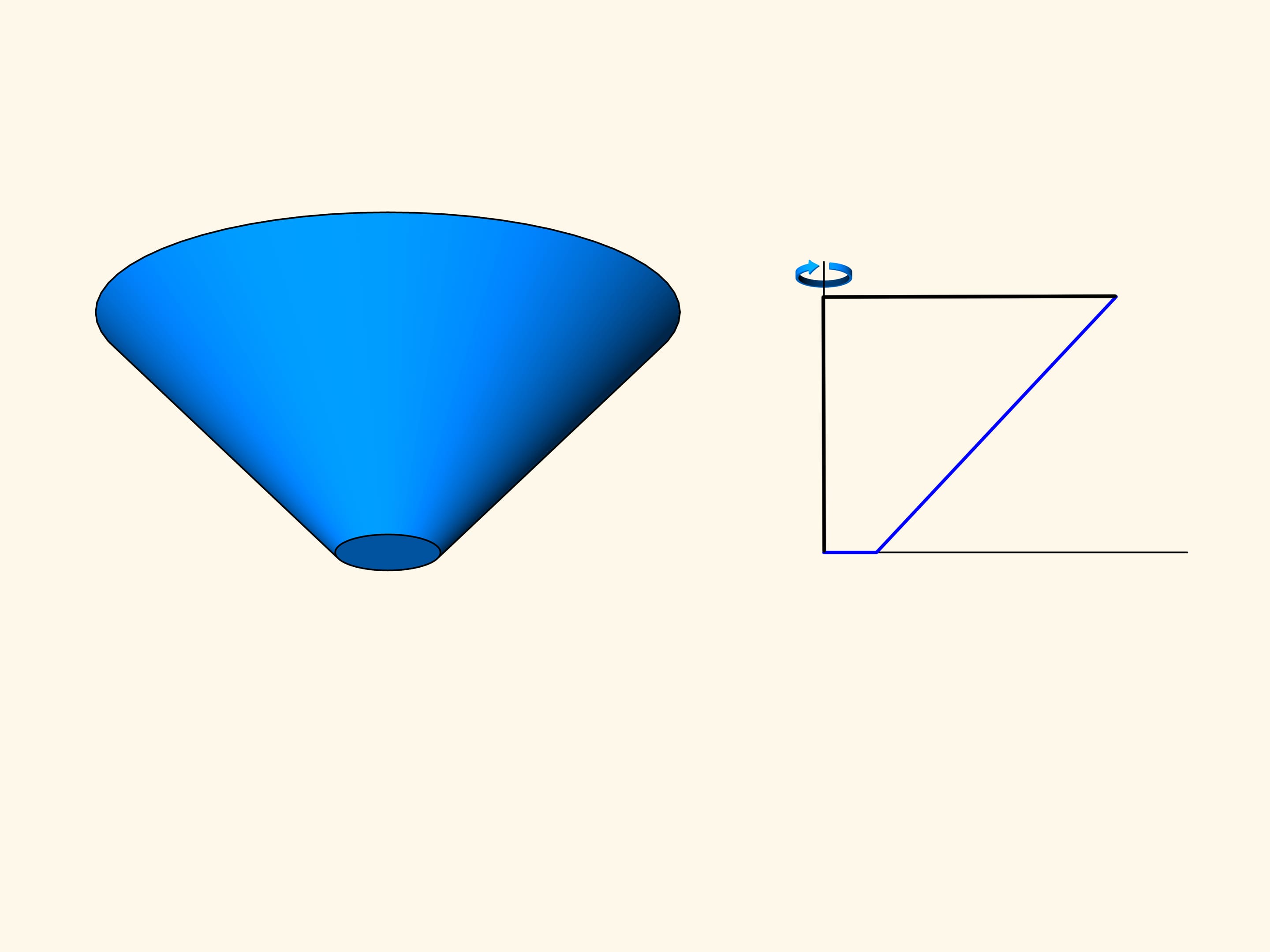
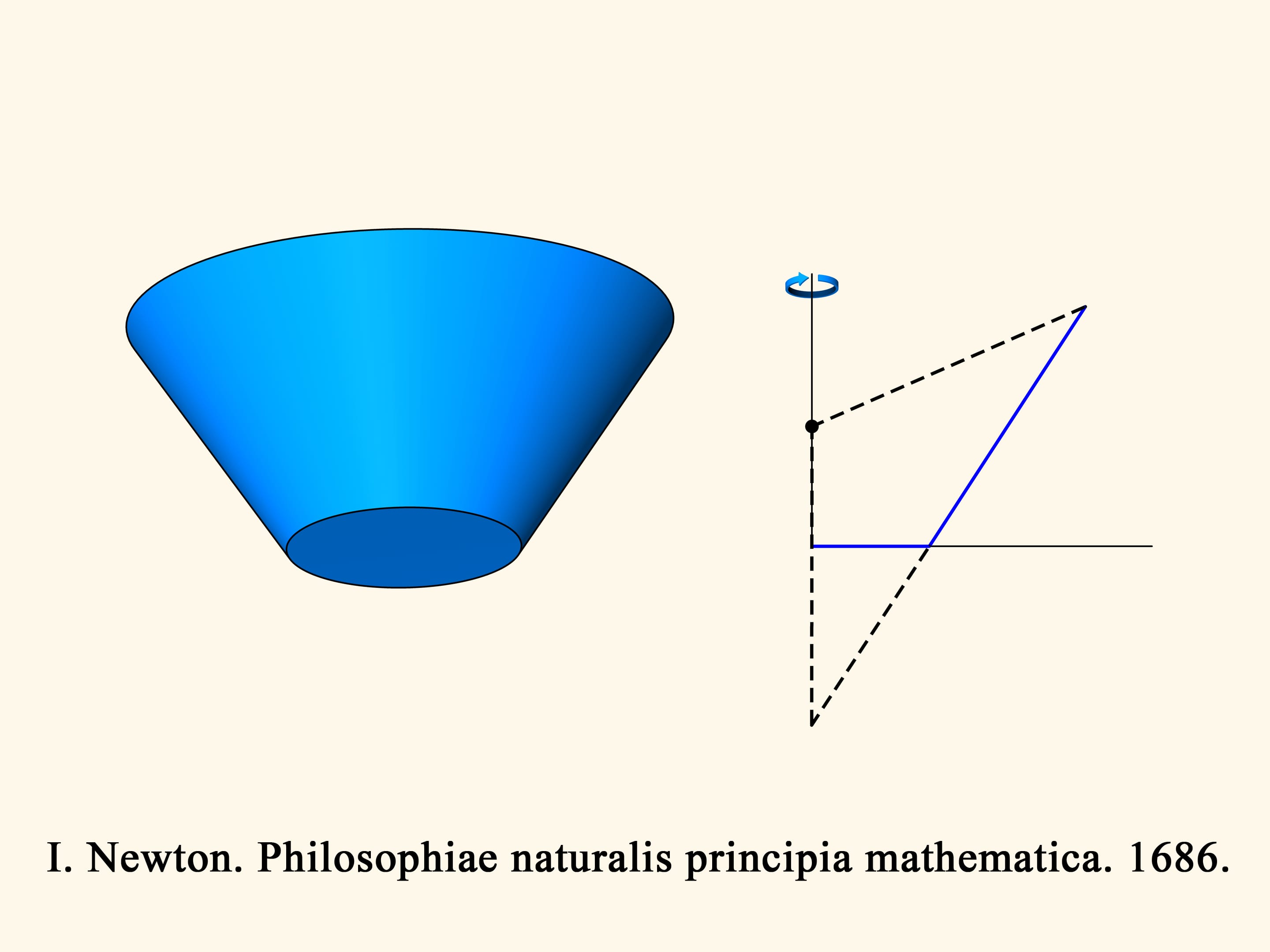
In a second time Newton begins to study the trun­cated cones: among all the trun­cated cones with the radius of the bigger base and the height fixed, find the one for which the resis­tance in a rarefied medium — for a motion along the axis of the cone — is minimal.

Let us consider a section of the trun­cated cone and the problem in the planar case.

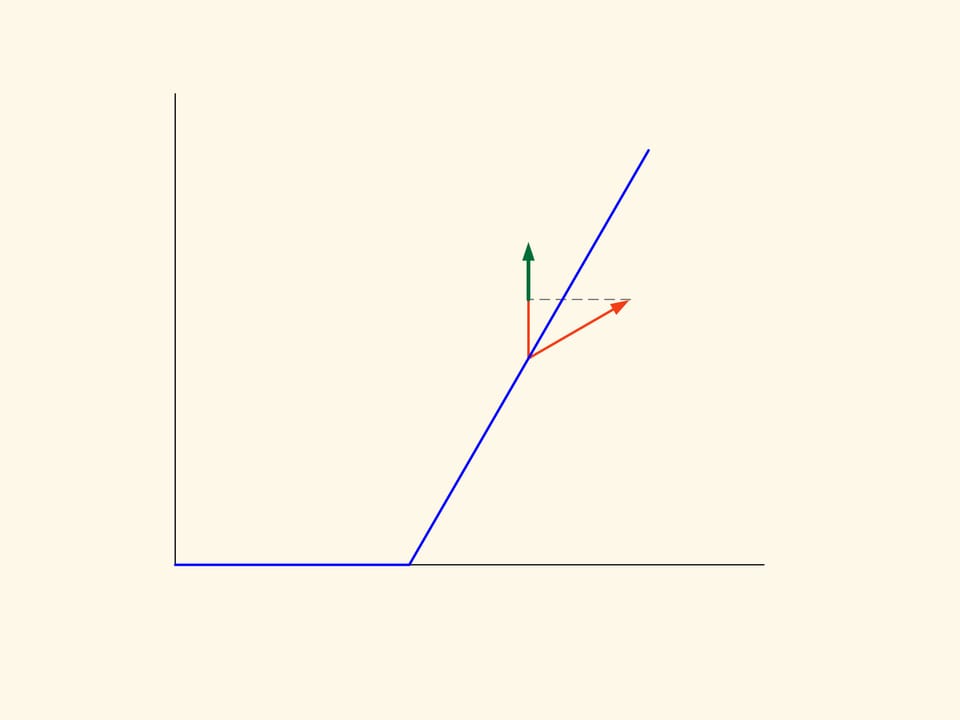
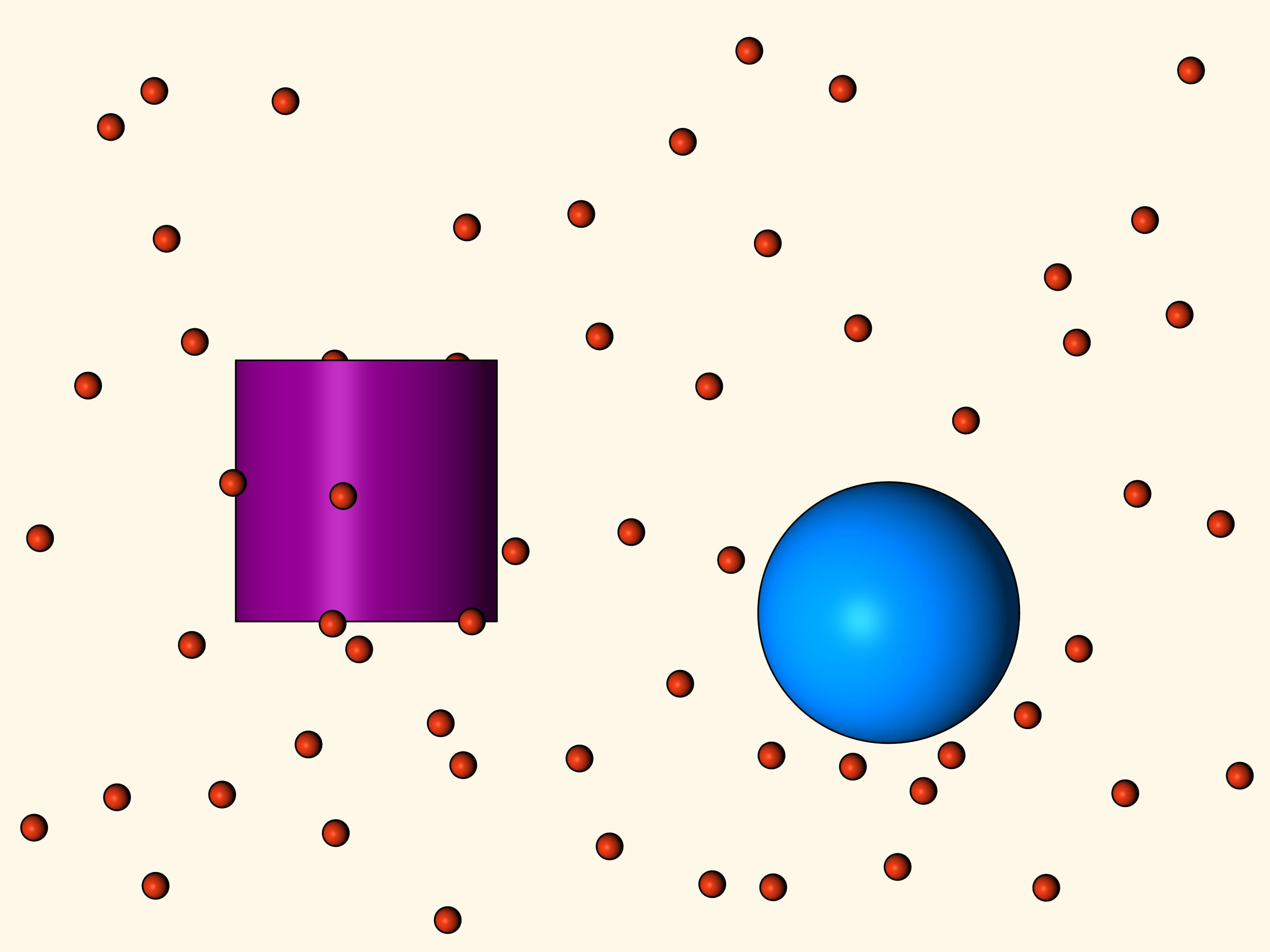
What is the resis­tance? While the cone falls, it collides with the spheres — the parti­cles of the rarefied medium. One part of the spheres collide with the lower surface of the trun­cated cone, and a part with the lateral surface, some of them move without stop­ping and without suffering the effect of the body. When it collides with the trun­cated cone a particle changes its direc­tion of motion according to the law that “the angle of inci­dence equals the angle of reflec­tion”. The resis­tance that the sphere has put up to the fall of the trun­cated cone consists in the change of the vertical compo­nent of the momentum vector of the sphere. Since the sphere evenly on average hit the surface of the body, the thrusts to the left and to the right cancel out and should be not consid­ered.

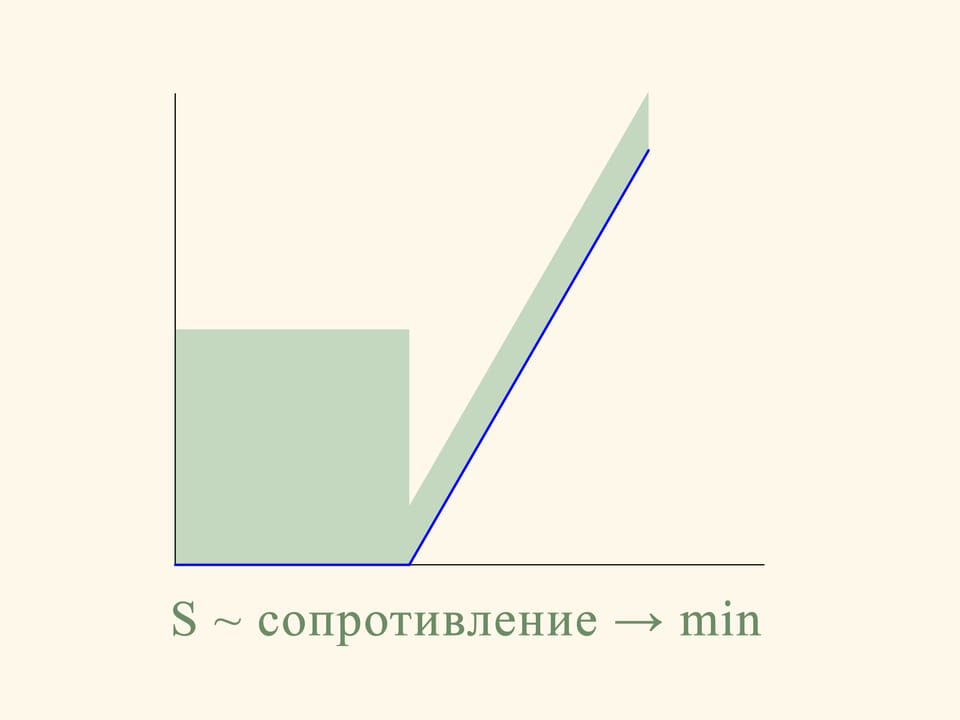
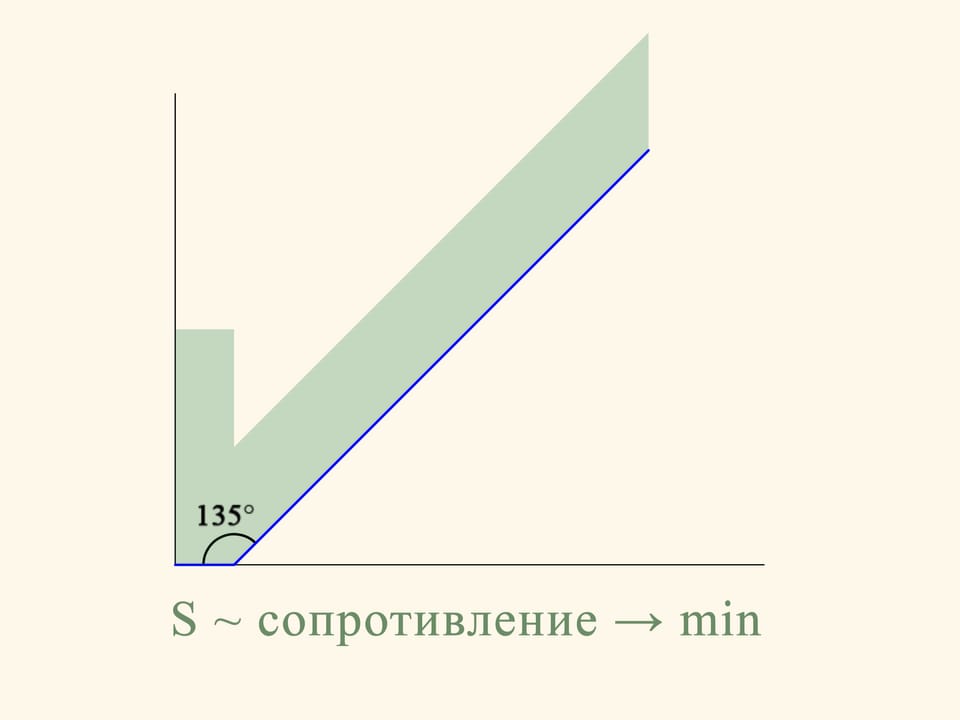
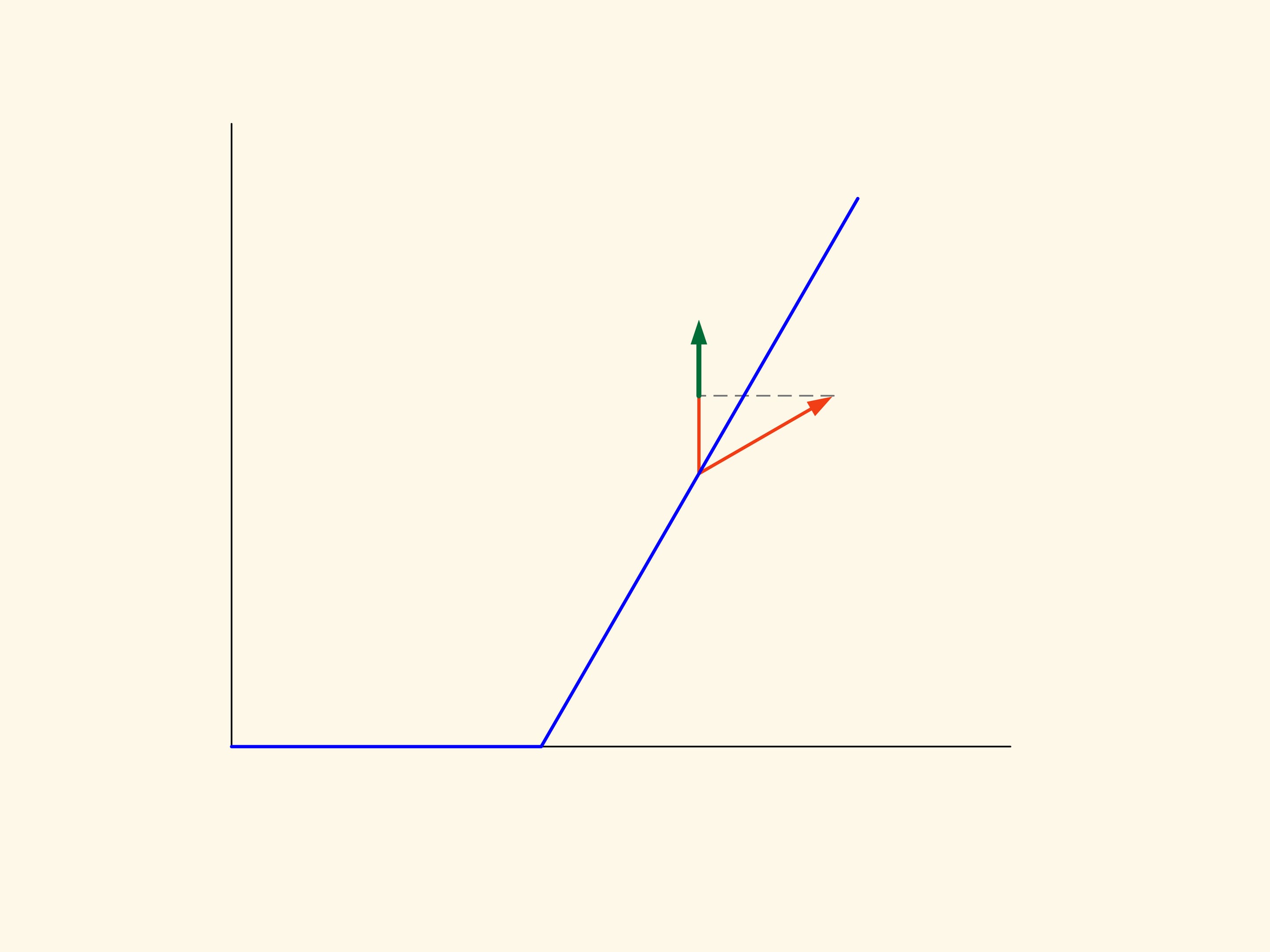
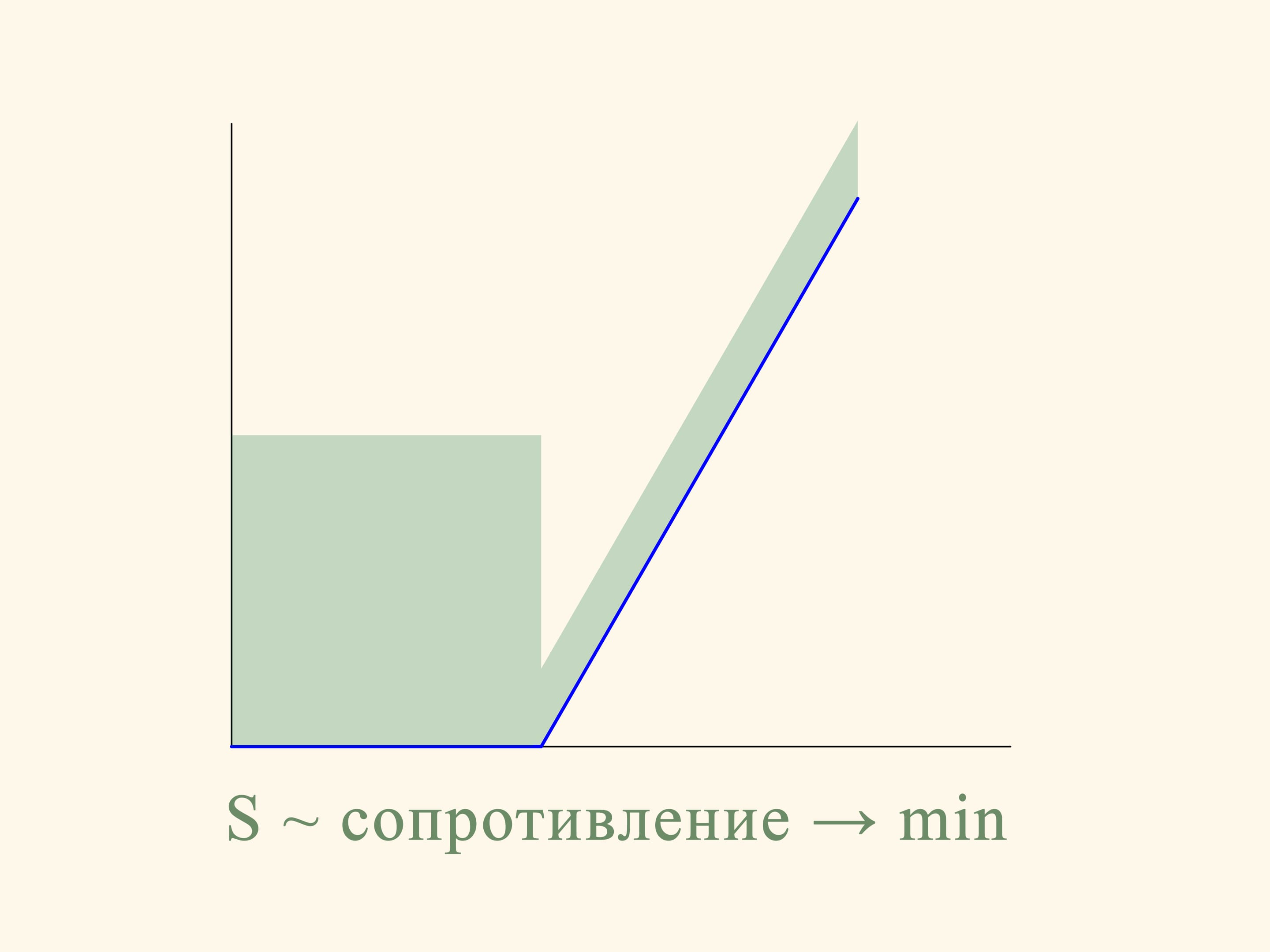
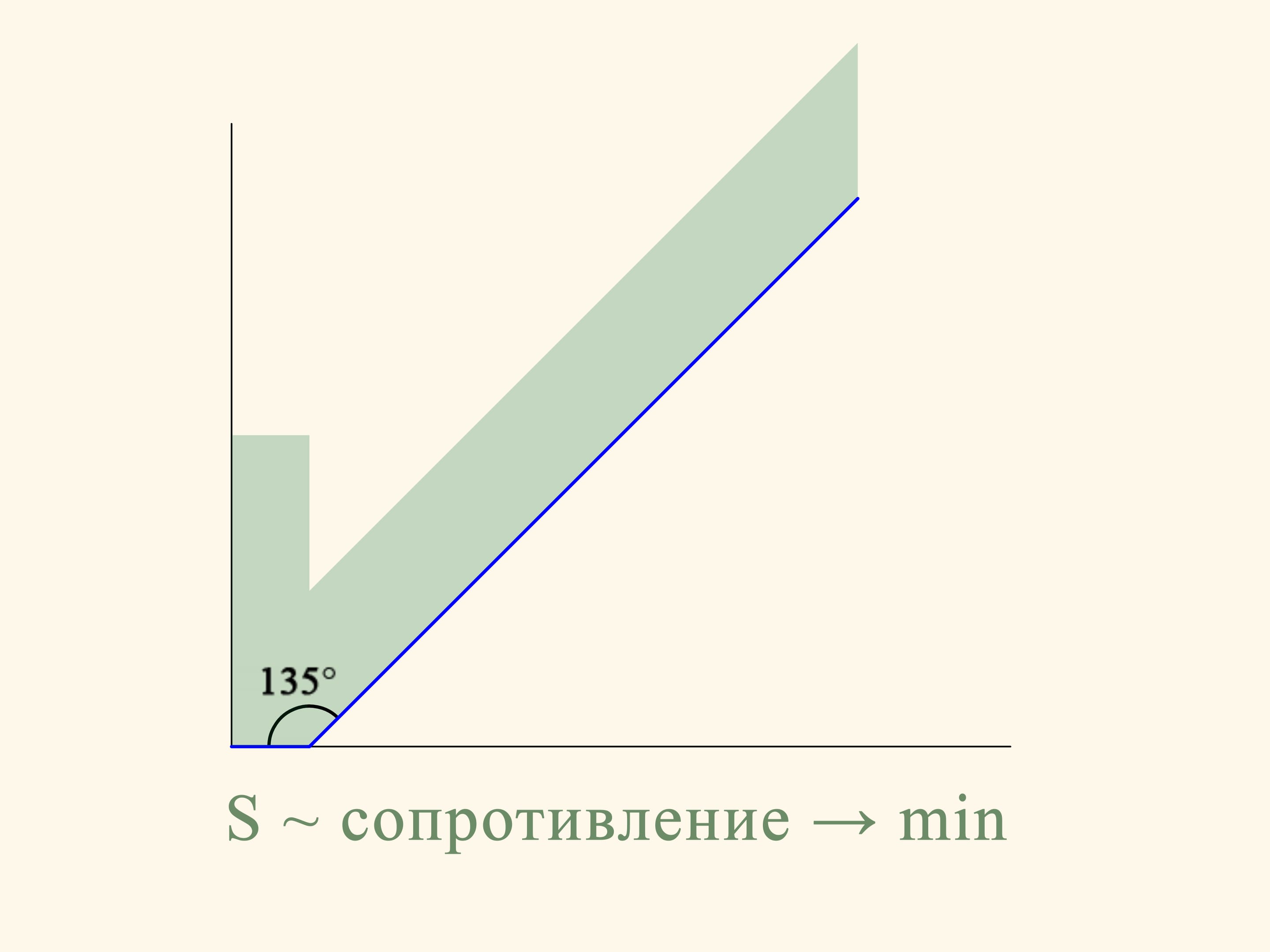
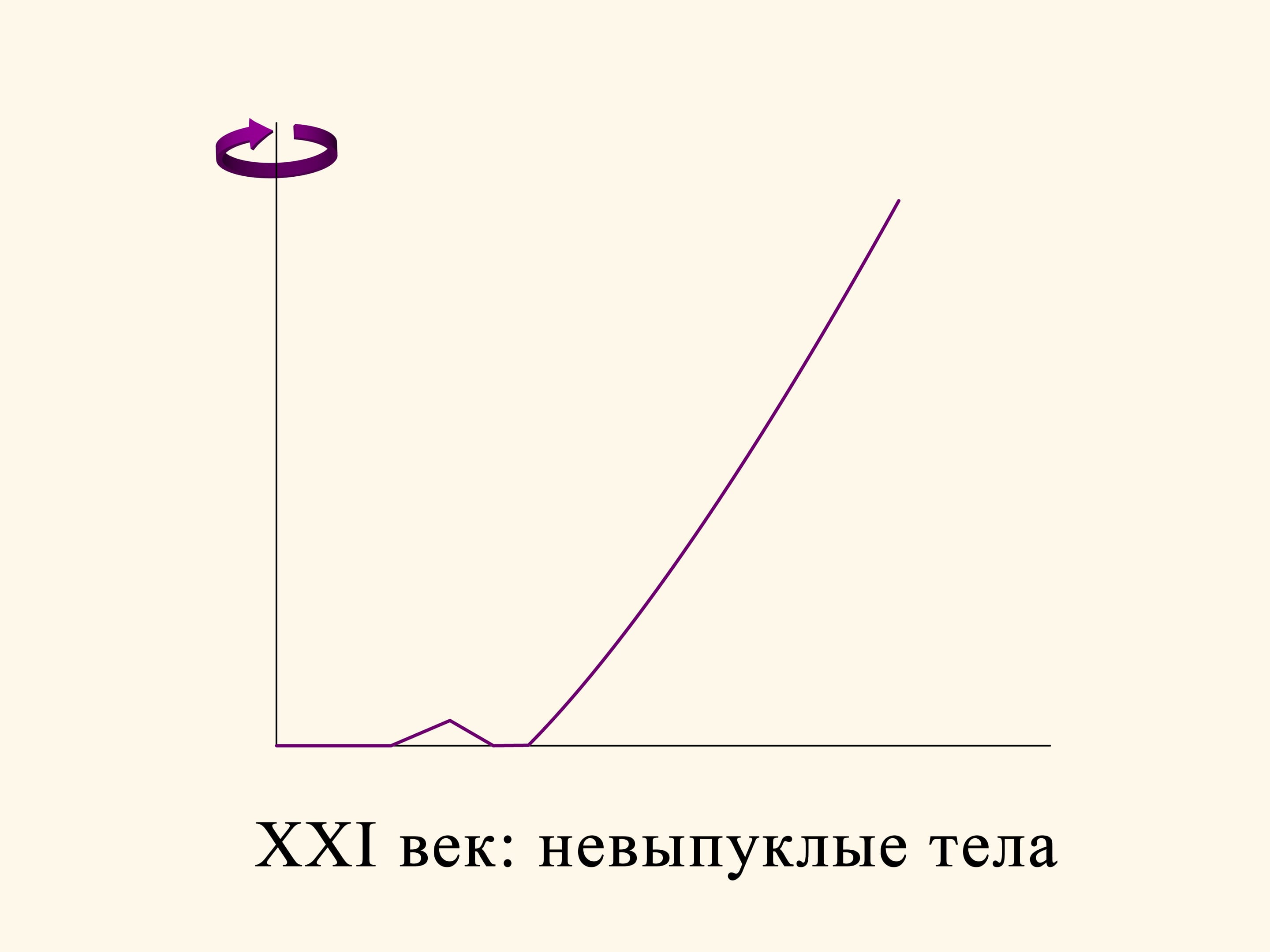
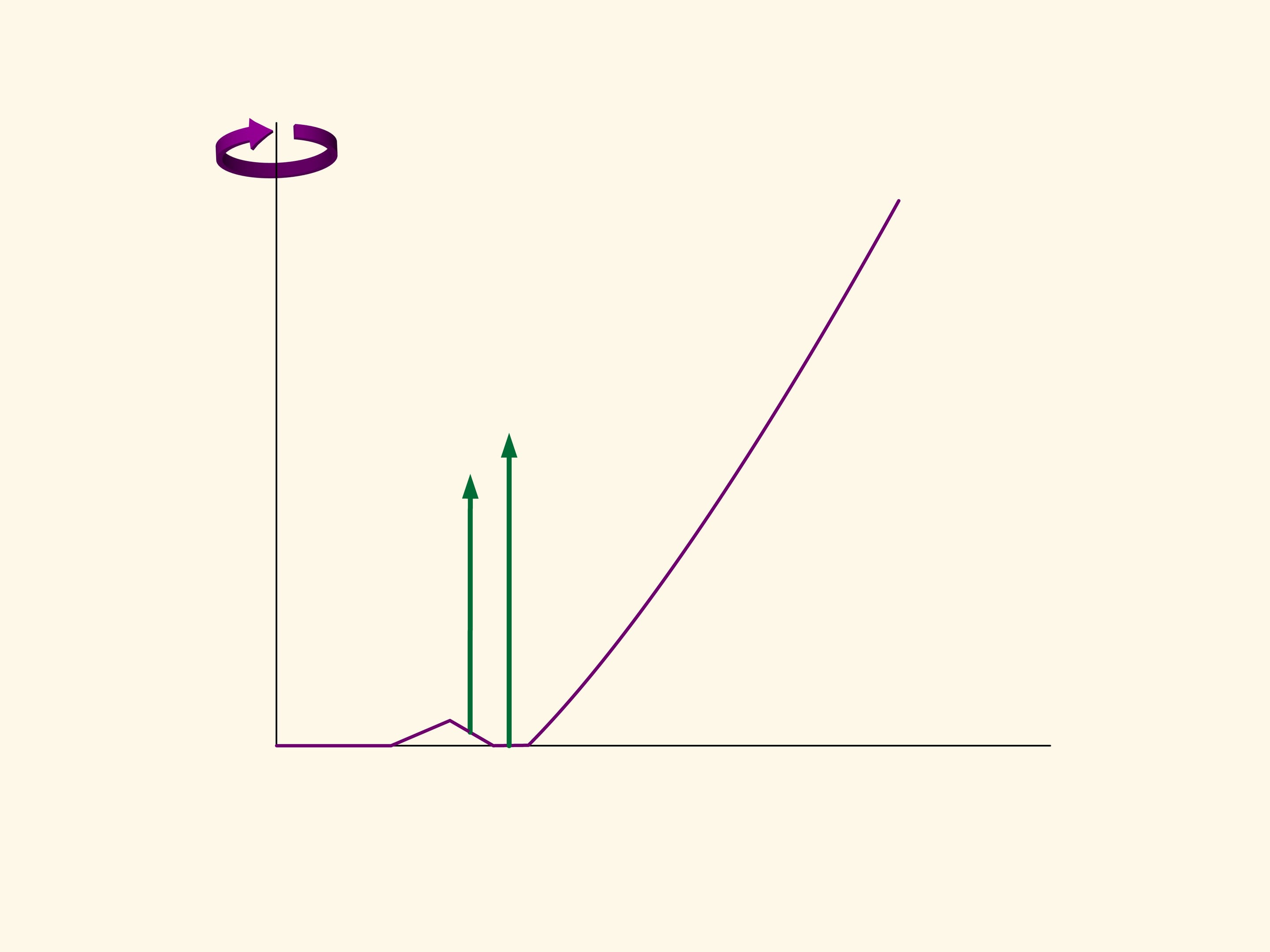
In the planar case the resis­tance of the section of the trun­cated cone is propor­tional to the sum of the area of a rectangle constructed on the smaller base of the trapezium and the area of a paral­lel­o­gram, constructed on the oblique side. And this resis­tance must be mini­mized. If we do the calcu­la­tion, we find that the area of the figure in green is minimal when the angle between the base and the oblique side is equal to 135°. That is, the sphere after the colli­sion with the oblique side moves in a strictly hori­zontal direc­tion.

From the planar solu­tion of the problem, can we deduce that the section of the optimal trun­cated cone will satisfy the same condi­tion for the three-dimen­sional problem? It turns out that this is not true. To move from one section of an object to the object itself, we must rotate the planar section around the vertical axis. The small pieces of the surface farthest from the axis, contributing to the area, describe during the rota­tion a trajec­tory much longer and will there­fore make a greater contri­bu­tion to the volume. By conse­quence, we cannot find the minimum volume in the three-dimen­sional problem using the minimum of the area in the plane.

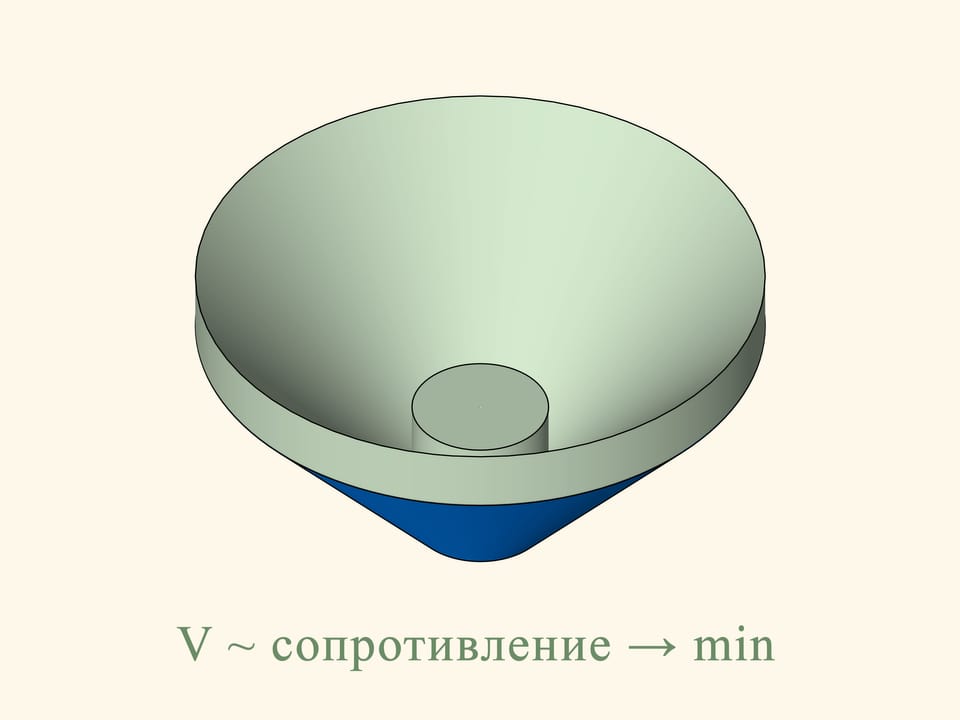
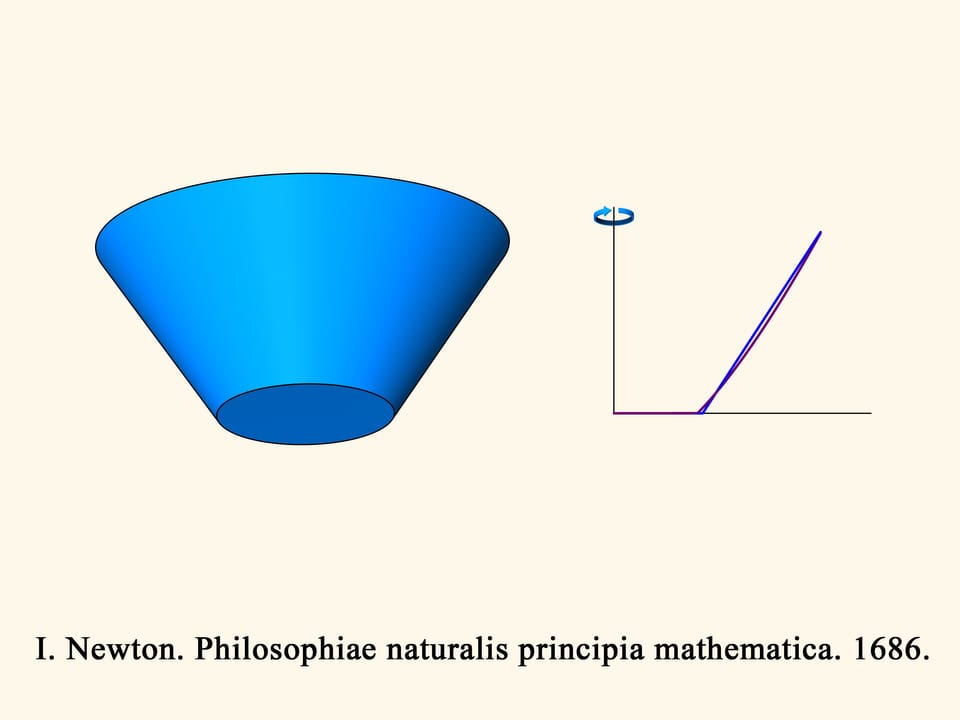
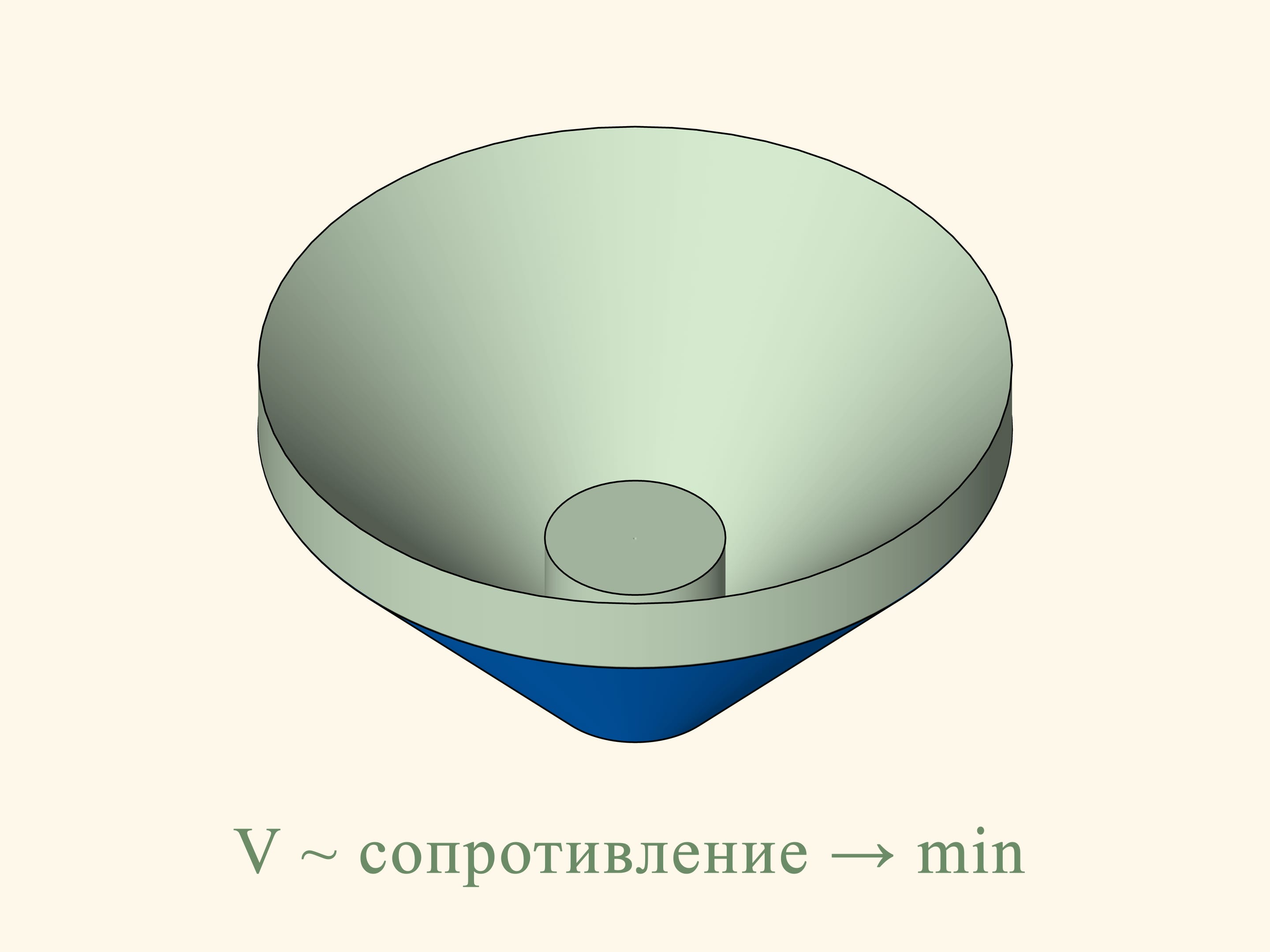
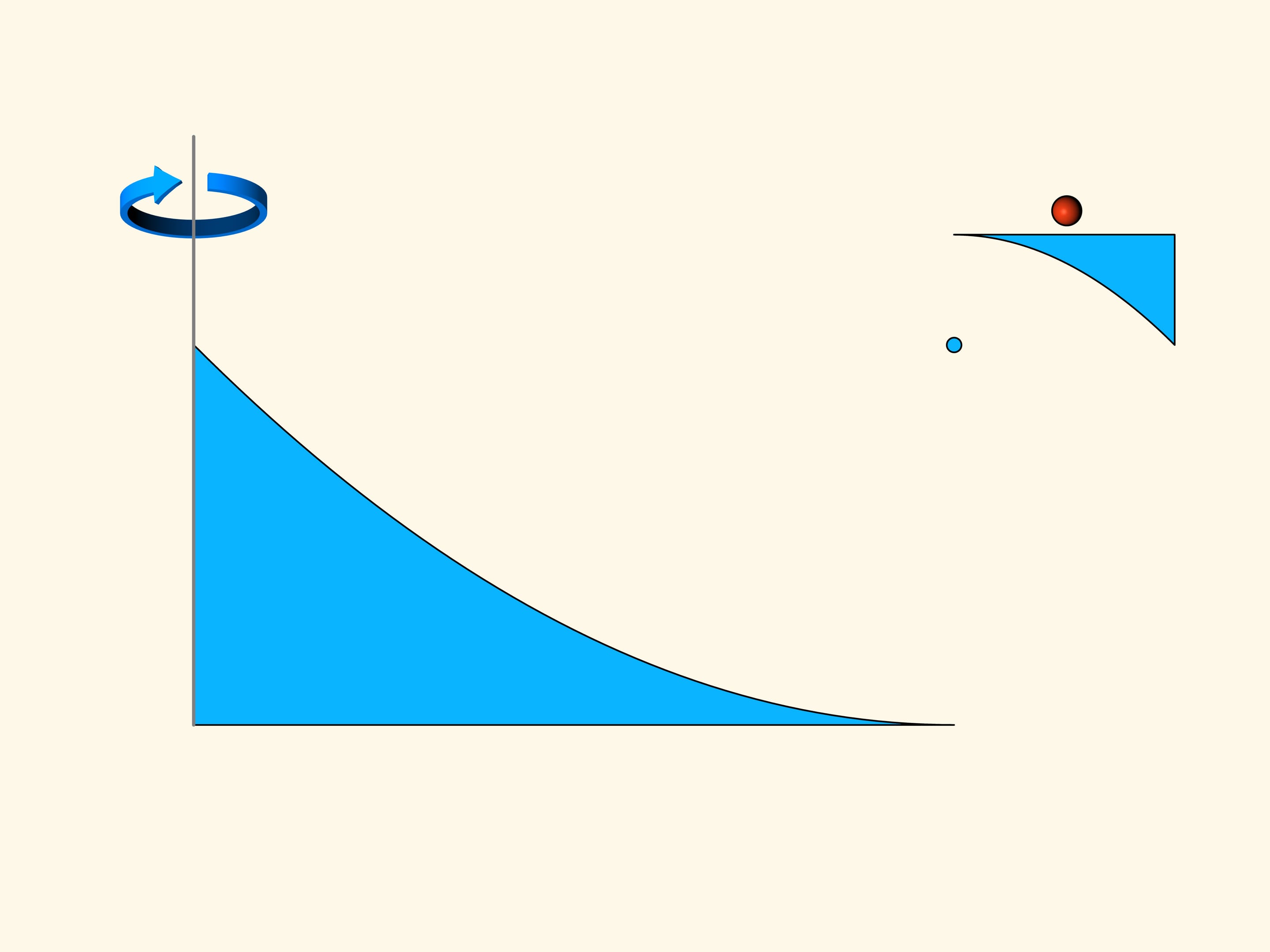
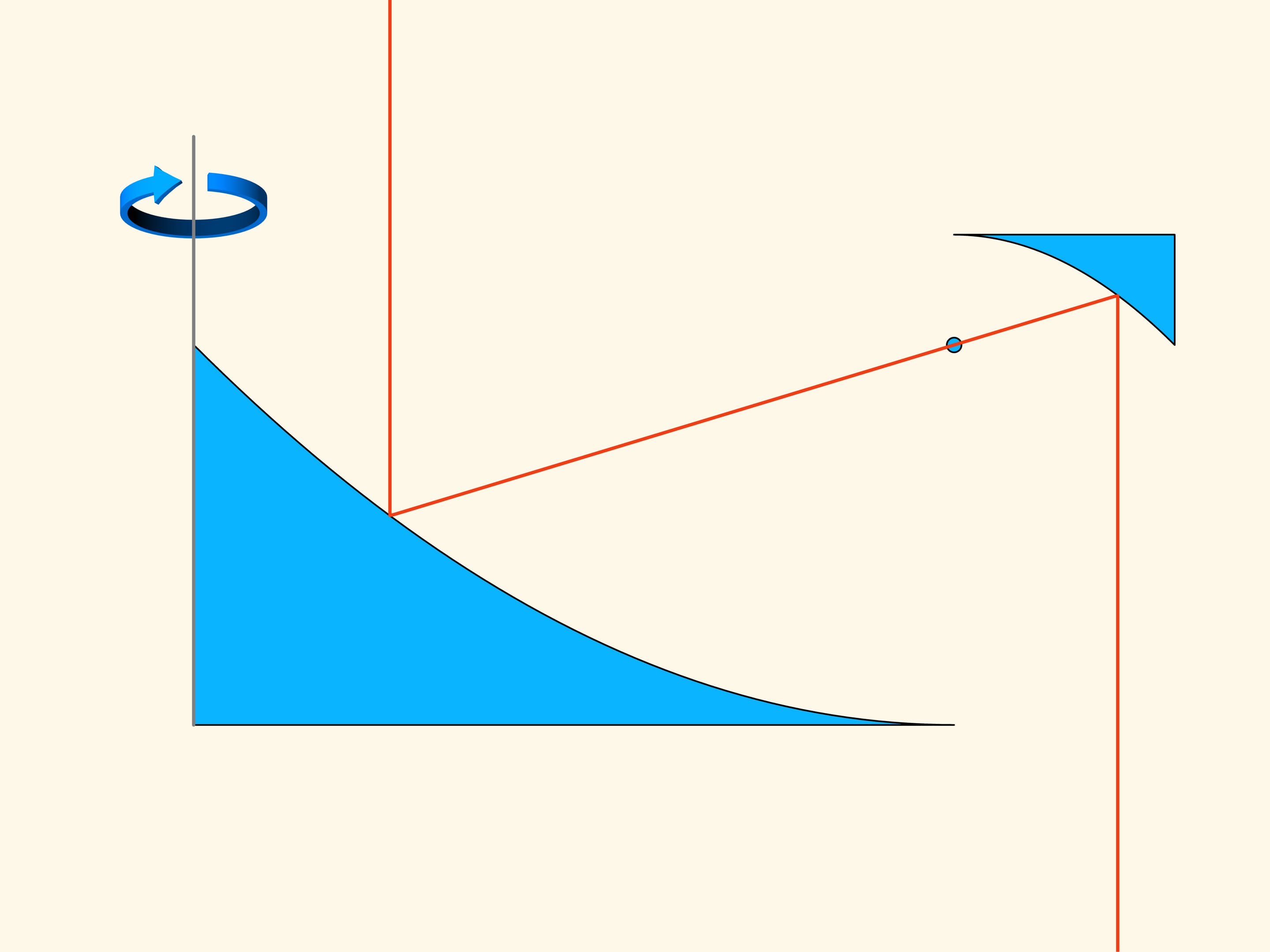
In the three-dimen­sional case the resis­tance of the blue cone is propor­tional to the volume of the green solid, and we have to find the minimum of this volume, among all trun­cated cones. Newton shows that the trun­cated cone will be optimal — i.e., it meets the least resis­tance — under the following condi­tion. Take the midpoint of the height of the trapezium and connect it with the extreme point of the base by a straight segment. Add a vertical segment of this length below the midpoint consid­ered. The optimal cone is obtained by rotating the base of the isosceles triangle thus obtained. It is surprising that the solid that meets the least resis­tance is not a cone but a trun­cated cone!

But what will be the best convex solid of revo­lu­tion, best in the sense of least resis­tance, with a given width and a given height? Although at that time the vari­a­tional calculus did not exist yet (these prob­lems are now solved by this method), Newton finds the answer to this ques­tion. He shows that the best convex solid of revo­lu­tion does not differ much from the optimal cone, and calcu­lates the exact gener­ating curve of this solid.

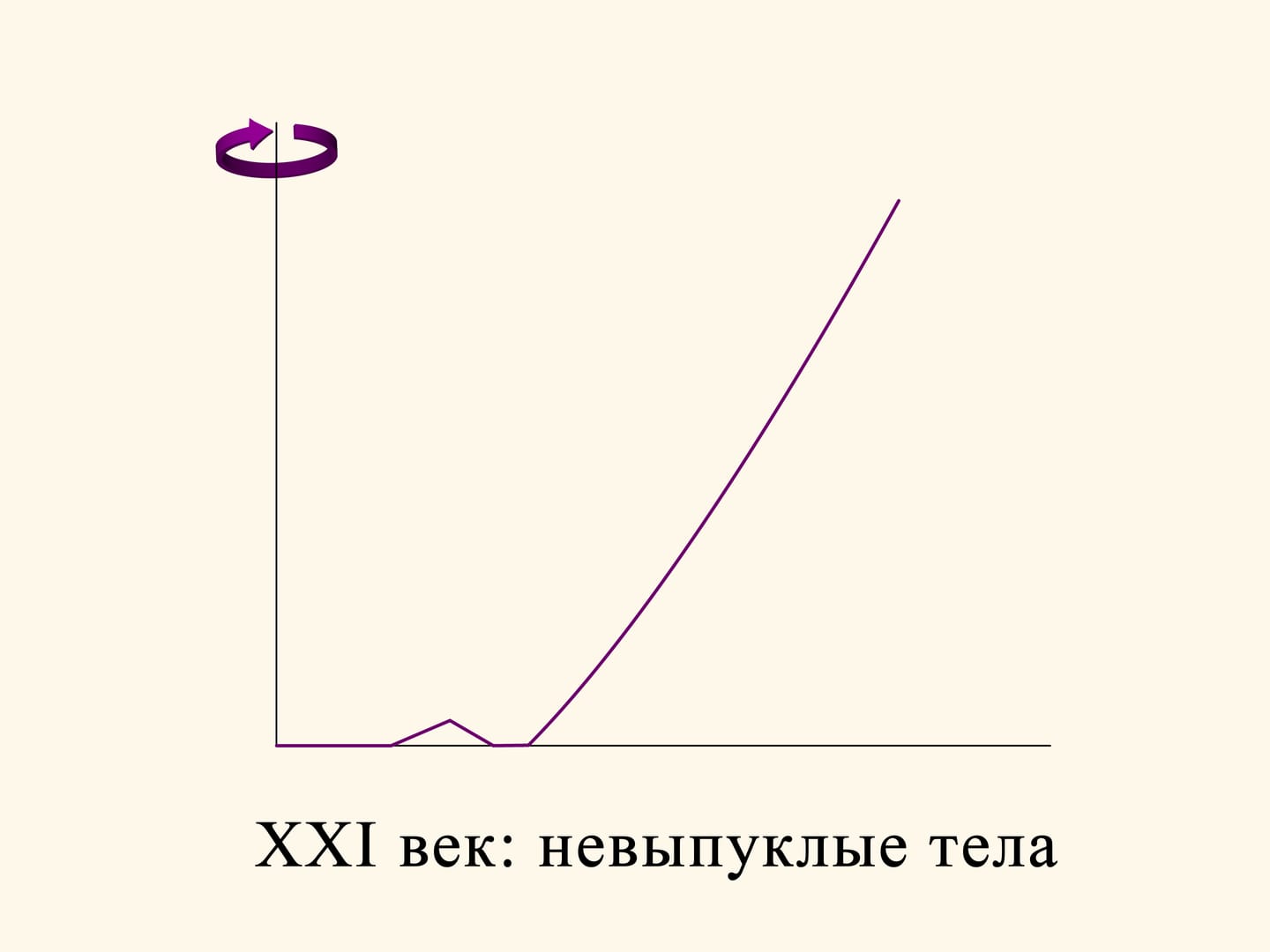
Since the time of Isaac Newton, for more than 300 years, scien­tists consid­ered the aero­dy­namic problem in a rarefied medium in its initial formu­la­tion: find a convex solid of revo­lu­tion. It seemed natural that the best solid should be convex. Only in the twenty-first century math­e­mati­cians tried to waive the condi­tion of convexity, and this led to an amazing achieve­ment!

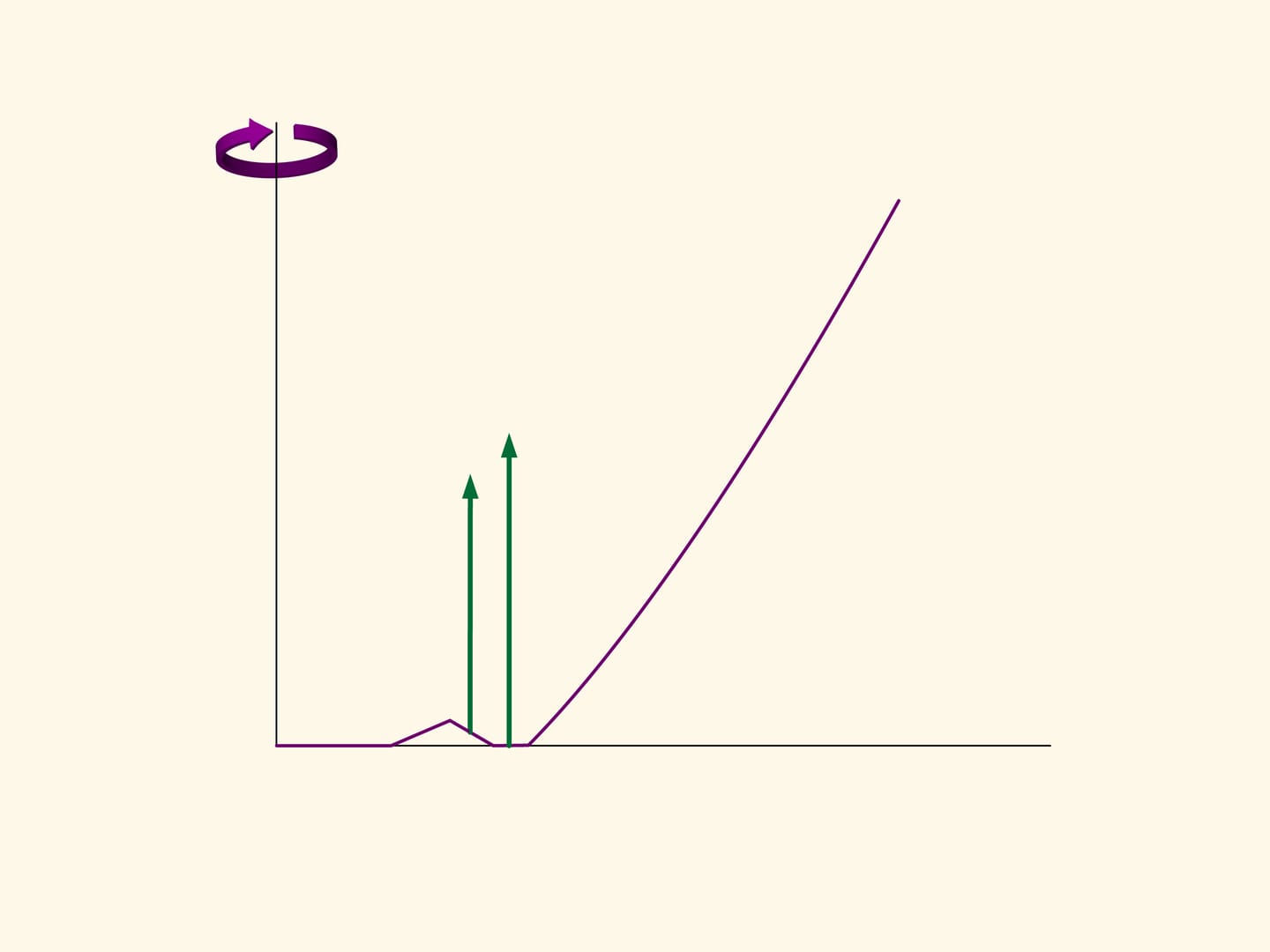
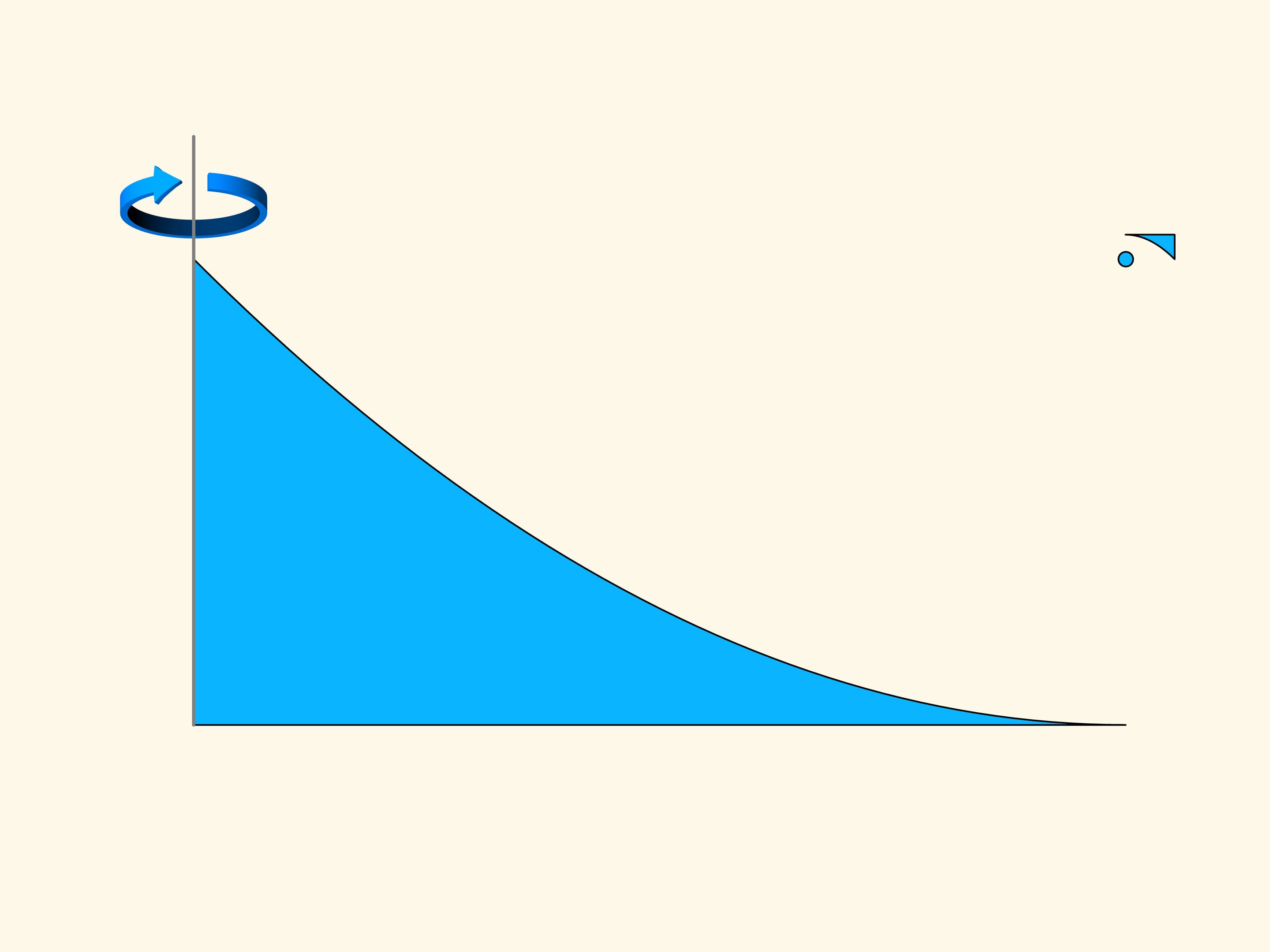
Take, for instance, the section of the optimal solid found by Newton, and make a trian­gular hole in its flat part. The solid of rota­tion obtained is already no more convex, but its resis­tance decreased with respect to that of the convex solid. In fact, if the groove is not too deep, then a sphere, after a colli­sion, bounces in oblique and does not collide with the solid any more. The vertical compo­nent of the momentum vector of the sphere, and, conse­quently, the braking impressed by the impact will be lower than for a rebound on a hori­zontal surface.

We will observe two inter­esting construc­tions of non-convex solids, exposed in the work of A. Yu. Plakhov.

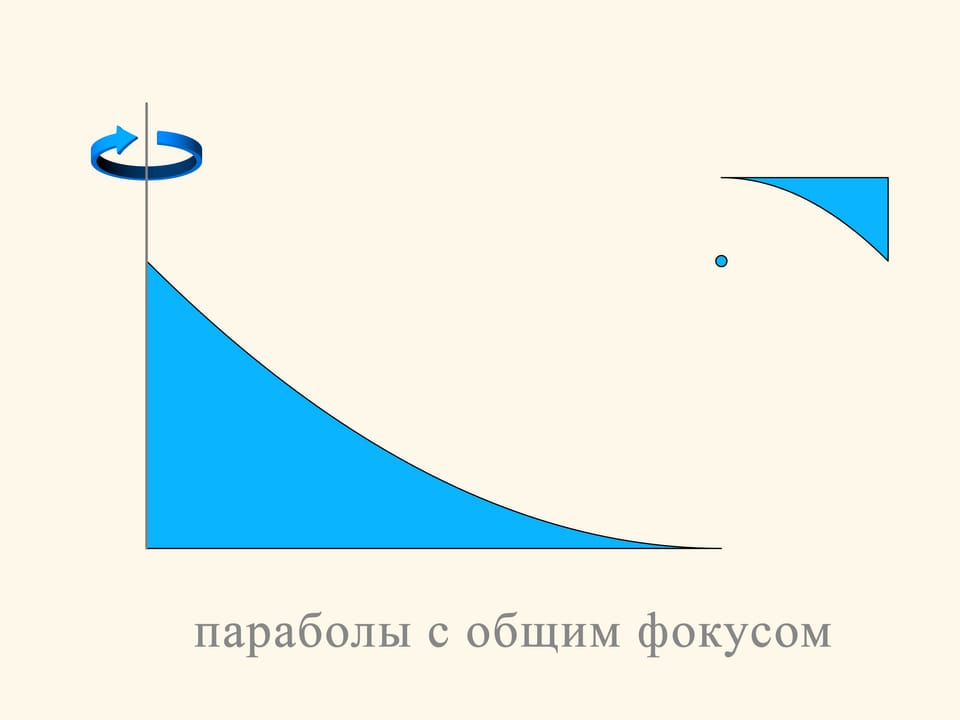
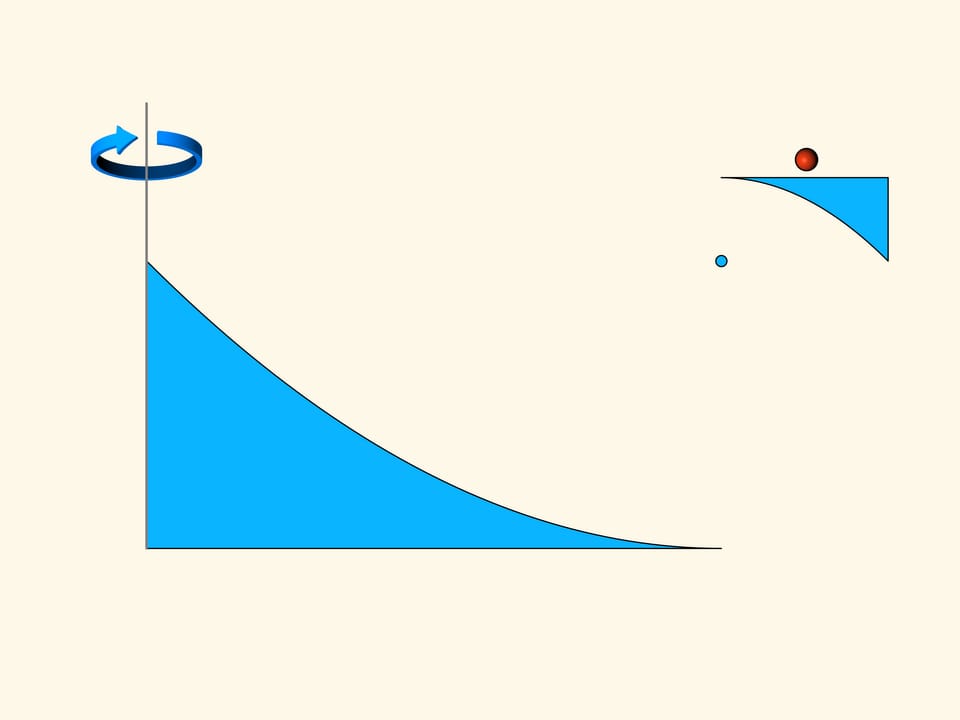
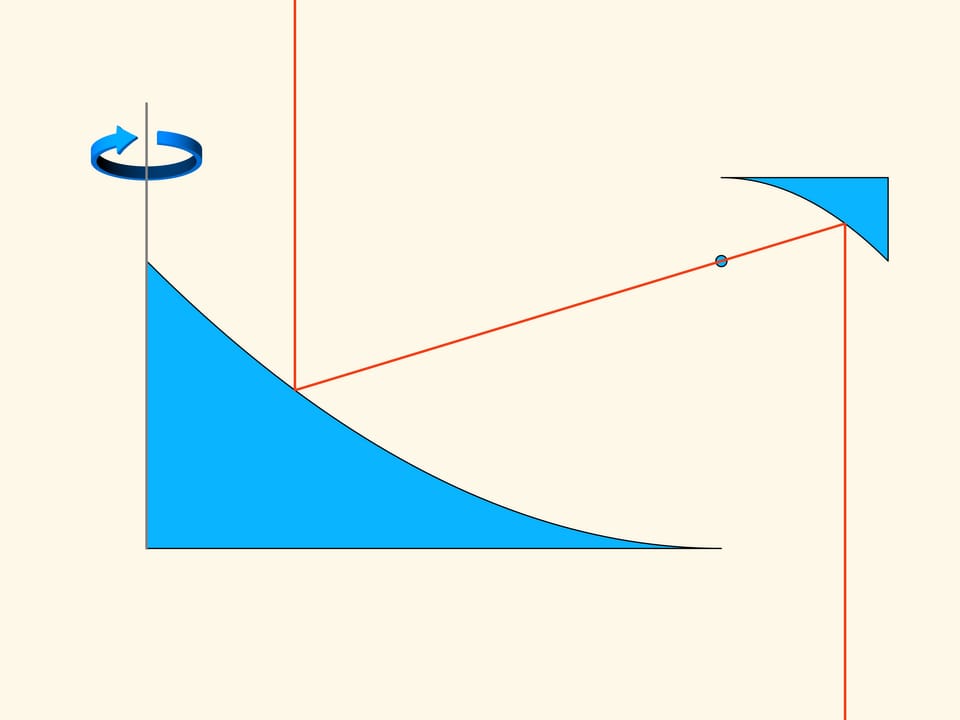
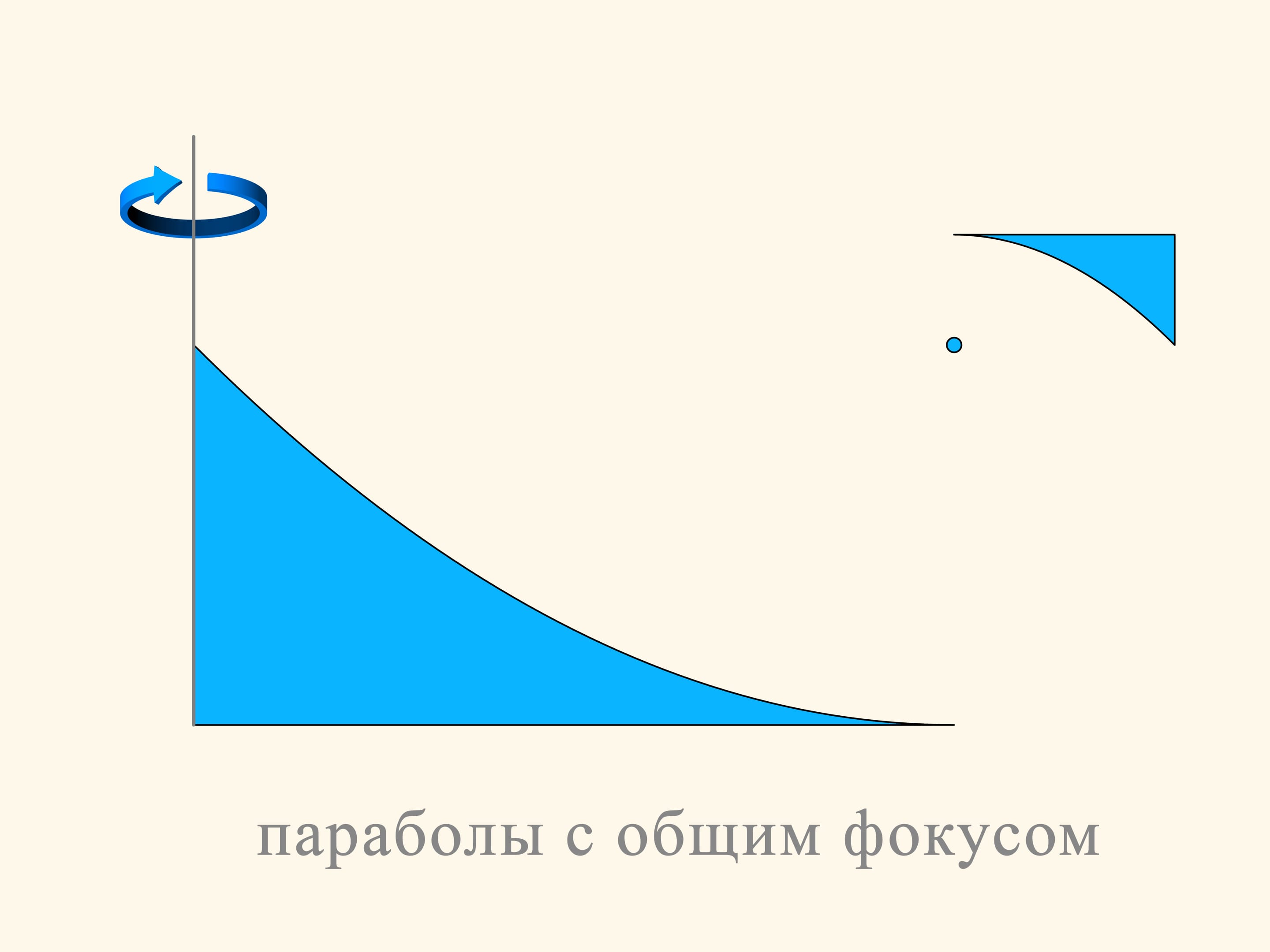
The plane section of the first construc­tion consists of two pieces of parabolas, arranged so that their focuses and their axes coin­cide. The motion will be in the direc­tion of the axis of parabolas. As you remember, the parabola has the optical prop­erty that the rays parallel to its axis, after reflec­tion on the parabola, pass through its focus. In the construc­tion we consider, part of the spheres that collide with it, fall into the hori­zontal segment tangent to the top of the small parabola and put up resis­tance to the motion. But most of the spheres are reflected by the big parabola, pass through the focus, and then are reflected by the small parabola and go away in a direc­tion parallel to the initial one. In the Newton rarefied medium these spheres do not increase the resis­tance because they do not lose the vertical compo­nent of their momentum, and after the colli­sions they exit in a direc­tion parallel to that with which they entered, only displaced in hori­zontal.

The part of the construc­tion that reflects the spheres can be made small, without changing the basic concept of the same construc­tion.

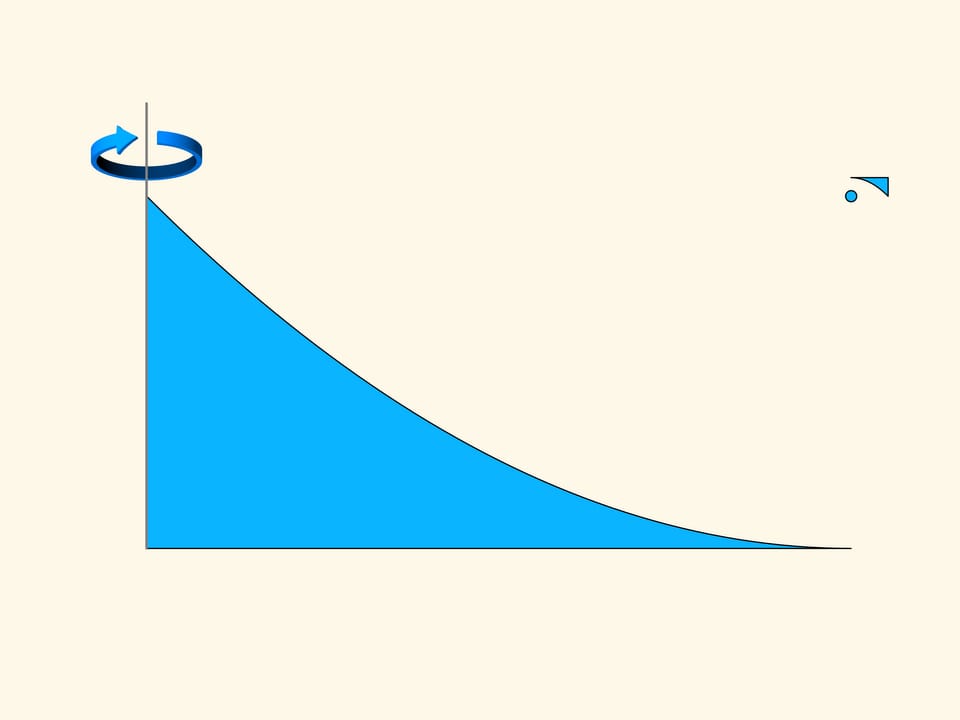
Let us rotate the construc­tion of the two parabolas about the vertical axis. We obtain a solid that recall a flying saucer. If we look at it from above, we see that the surface of this disk is very large. The surface on which the resis­tance is gener­ated can be made as small as we wish. For a motion in the direc­tion of its axis this solid of revo­lu­tion in a rarefied Newton medium will meet a resis­tance as little as we want.

But do they exist bodies with no resis­tance at all? It happens that also such bodies exist!

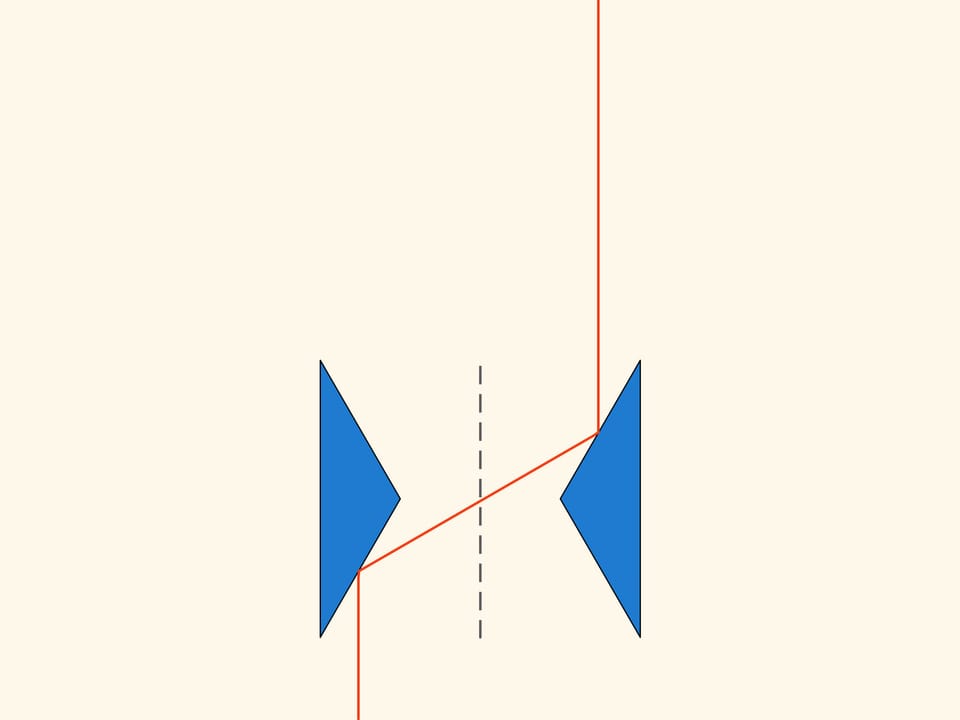
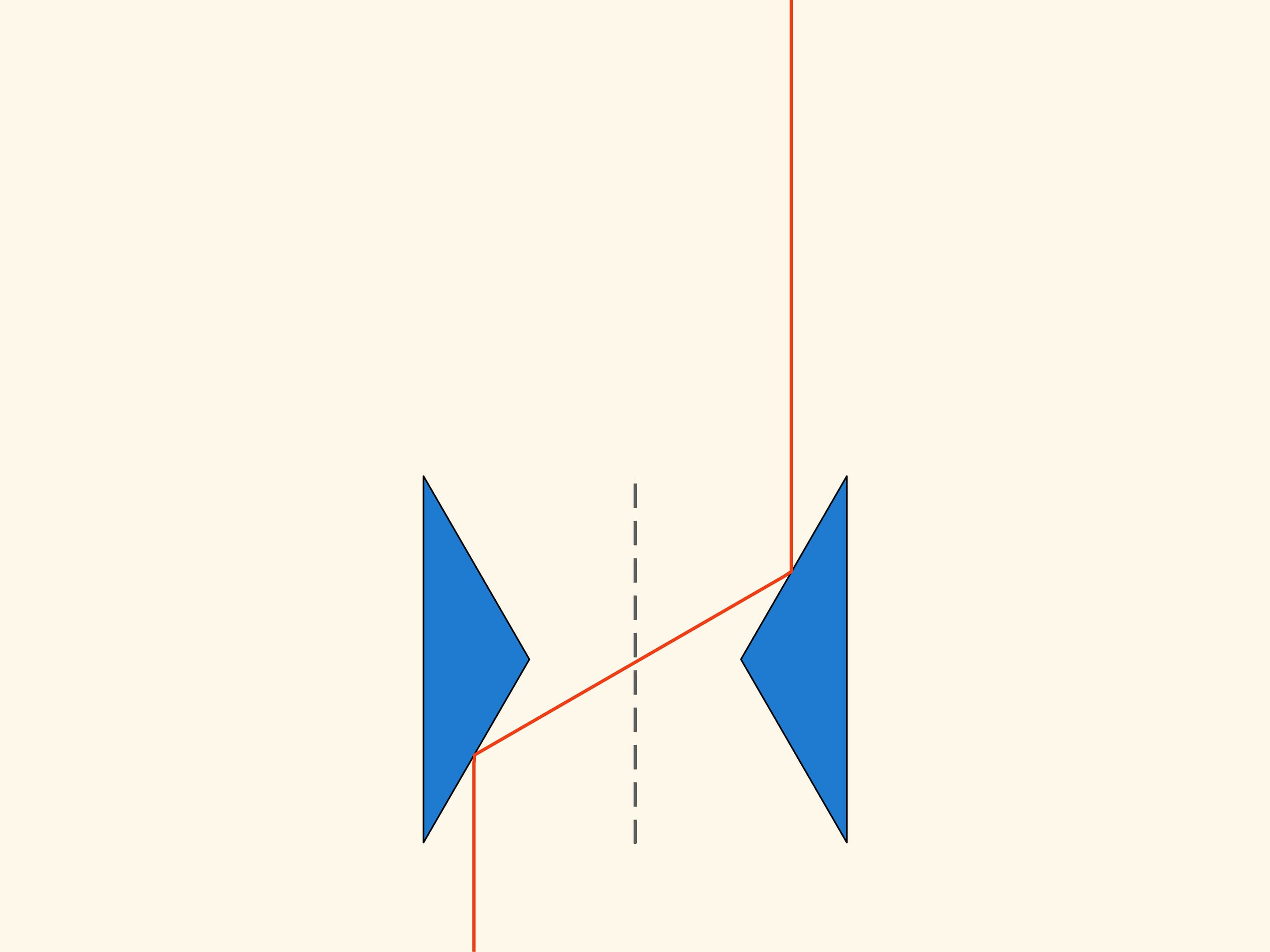
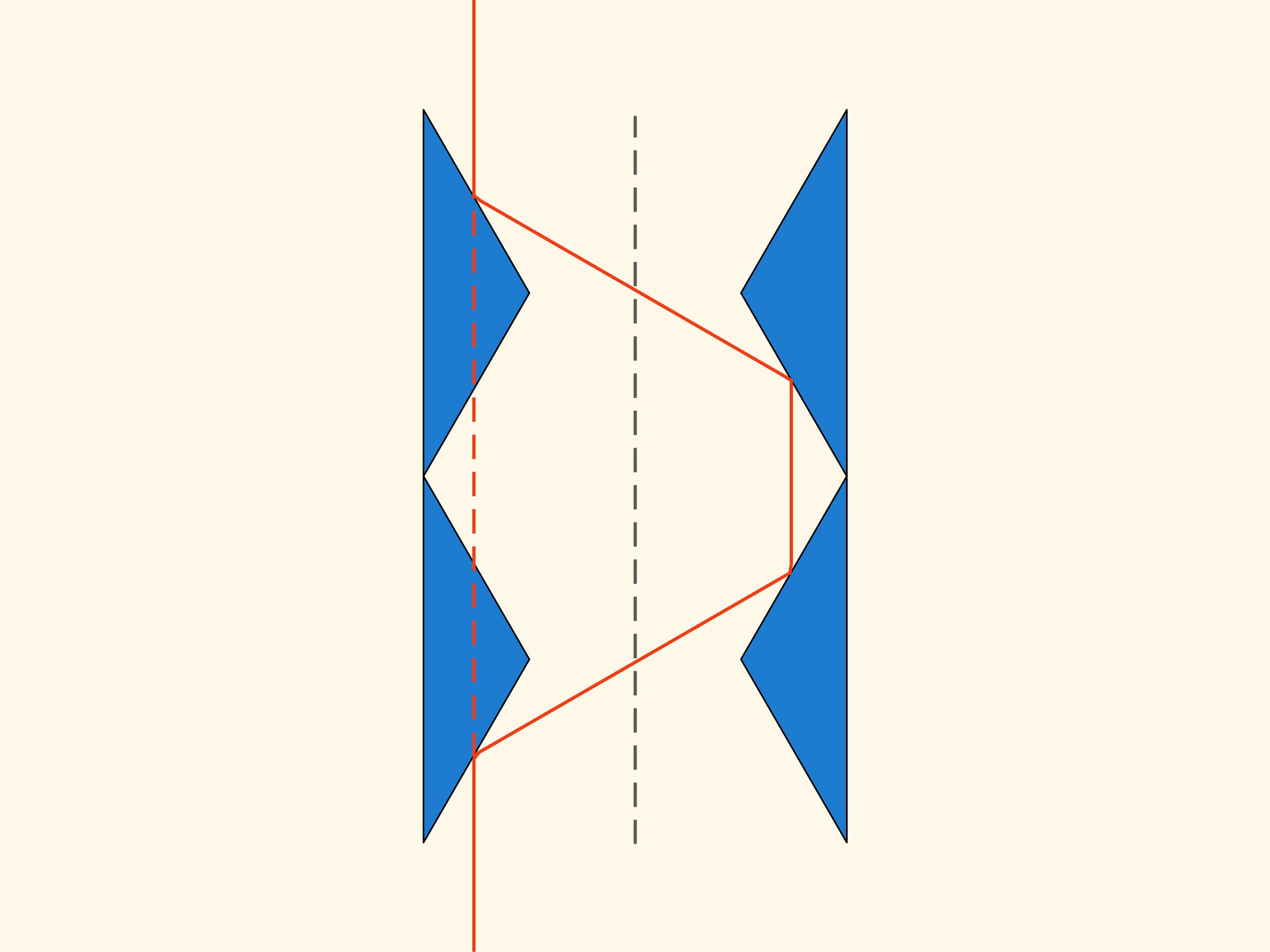
The construc­tion is based on a triangle with angles of 30, 30 and 120 degrees. Take another triangle symmet­rical with respect to the vertical axis at a distance of two heights.

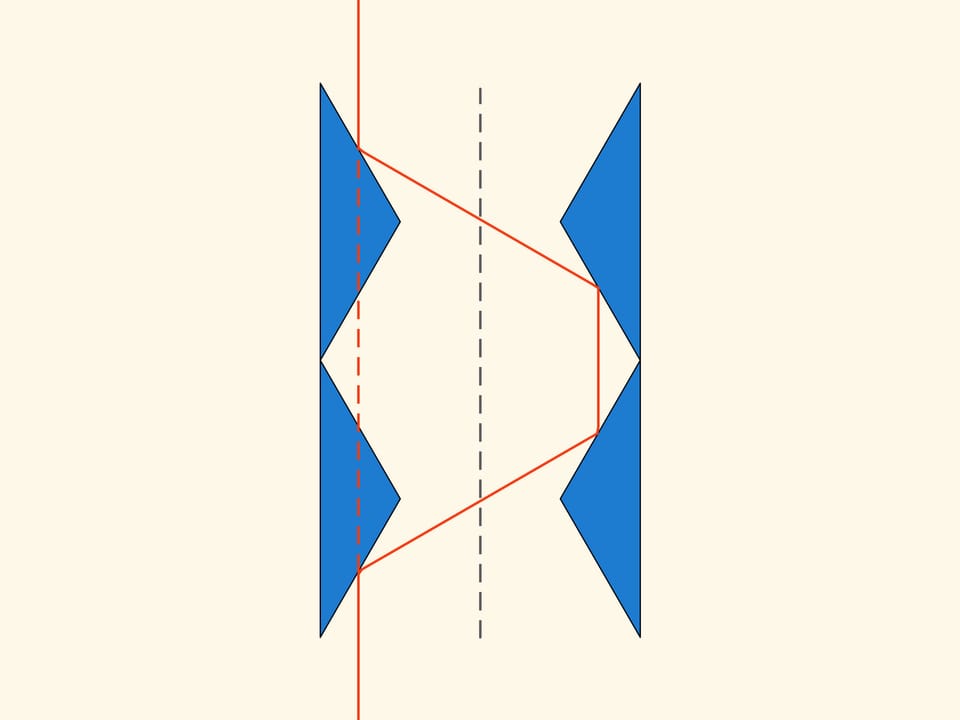
We look at what happens when this planar construc­tion moves in the direc­tion of the axis of symmetry in a rarefied Newton medium. With some spheres it will not collide at all, so that such spheres have no influ­ence on the motion. But those spheres, with which it collides, are always reflected on both the trian­gles and exit in a direc­tion parallel to the axis of symmetry, without changing their momentum vector. In this way, the resis­tance of the solid obtained by rotating this construc­tion about its axis of symmetry, is equal to zero!

To follow the trajec­tory of the spheres — the parti­cles of the medium — we have repre­sented their trajec­to­ries in the form of rays. But it is exactly along these trajec­to­ries that a ray of light prop­a­gates! If the last construc­tion of the two trian­gles is made of reflecting surfaces, then the right and left parts of the images that we see through it, are exchanged. But if we take a second iden­tical construc­tion and put it over the first, then the optical system so obtained will neither deflect the rays, nor reverse them.

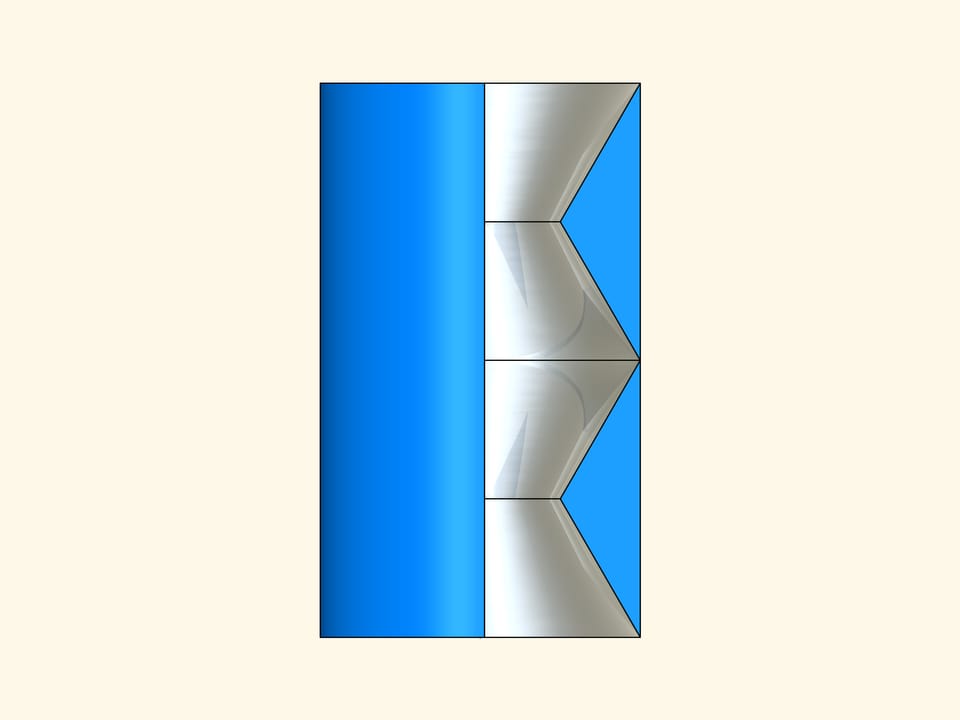
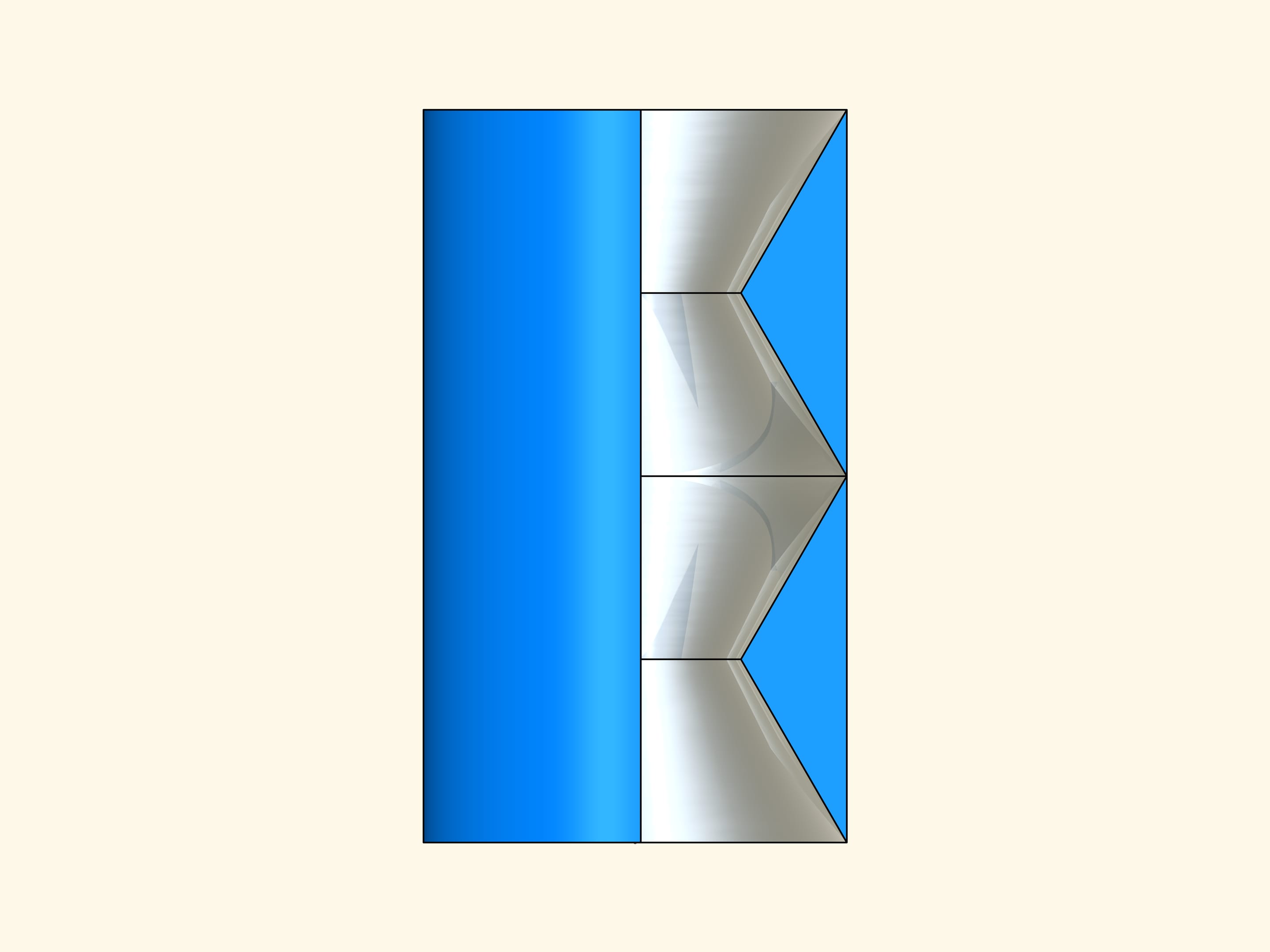
Now we rotate the planar construc­tion around its axis of symmetry and we ensure that all internal surfaces are mirror. We get a solid that from outside is a cylinder whereas inside is made of four conical reflecting surfaces. If we look through this cylinder along its axis of symmetry, then it will be invis­ible!

In his work, A.Yu.Plakhov also consider how to make an invis­ible envelop to any body. An object covered with a similar mantle becomes almost invis­ible!

Obvi­ously, these construc­tions do not deviate (or almost do not deviate in the case of the invis­ible mantle) only those rays that are parallel to the axis of symmetry. And for the human eye the “invis­ible cylinder” will be in fact almost invis­ible, only if seen from far enough. It is possible that some of you, using the knowl­edge of math­e­matics, and, perhaps, of other sciences, in the future be able to build objects completely invis­ible.