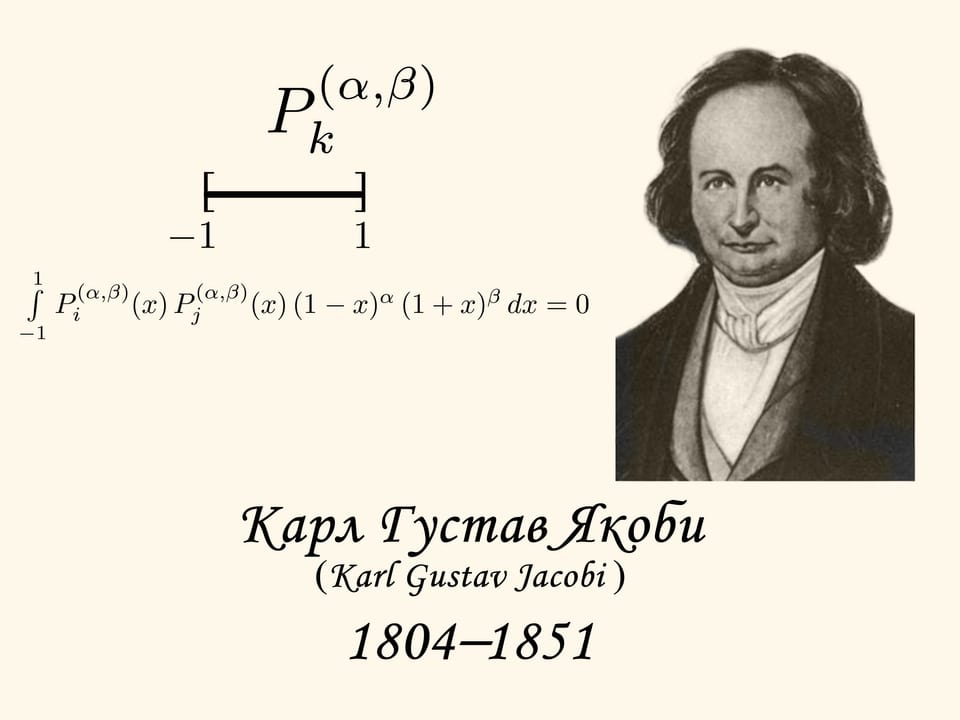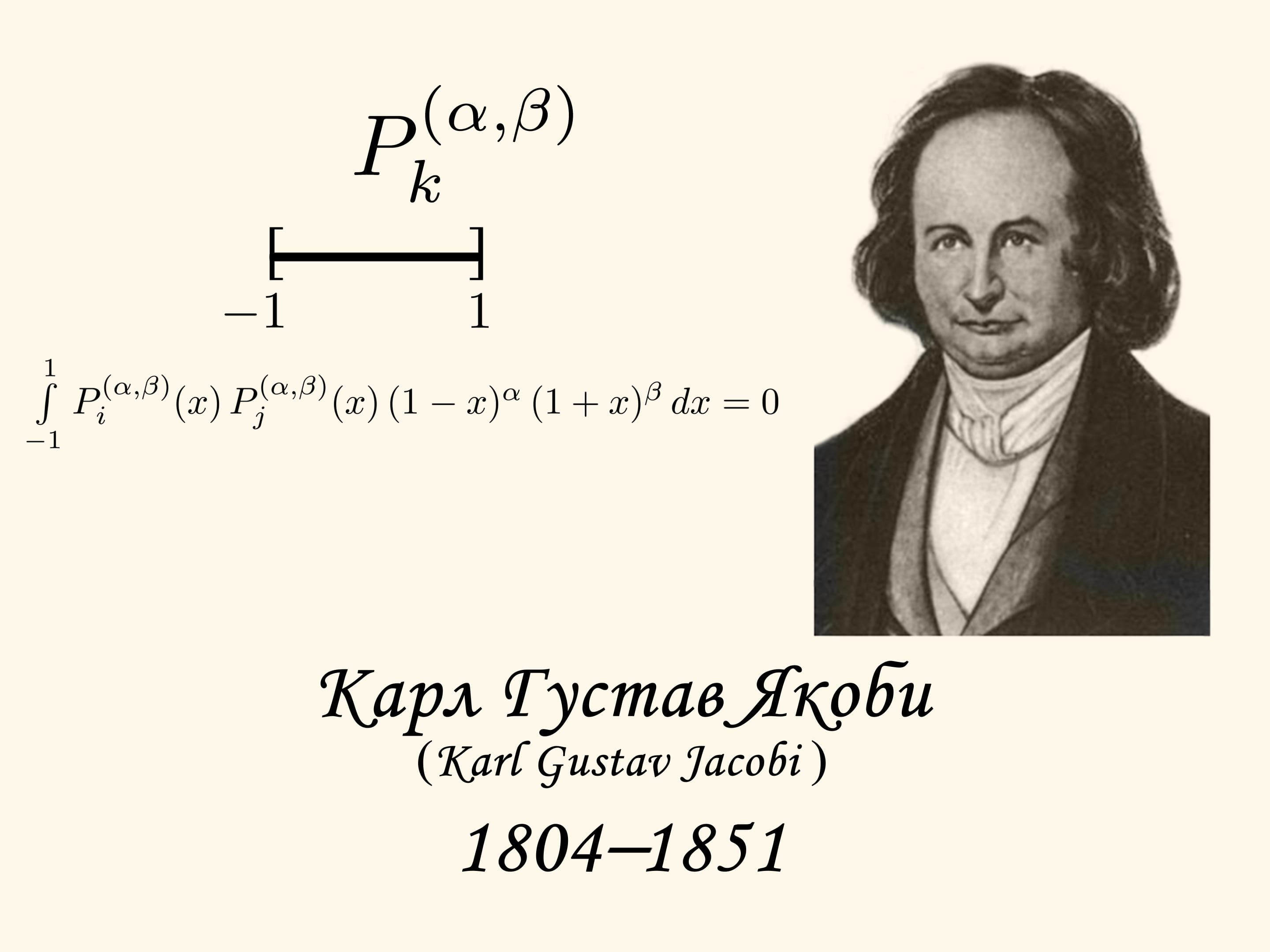Karl Gustav Jacob Jacobi lived in the first half of the XIX'th century. For his scientific research he developed a class of orthogonal polynomials, that were later named after him. Given some fixed values of the parameters $\alpha$ and $\beta$ (greater than $-1$) the Jacobi polynomial $P_{k}^{(\alpha, \beta)}$ is of degree $k$ and has thesame number of zeros lying in the segment $[-1,1]$.
The notion of orthogonality (i.e. perpendicularity) came from geometry to otherbranches of mathematics. If two vectors are perpendicular, their scalar productequals zero. By analogy two polynomials are called orthogonal if their scalarproduct equals zero. In this case by the scalar product we mean the integral overthe segment $[-1,1]$ of the product of two polynomials multiplied by a specialfunction that called weight.
Classes of orthogonal polynomials play a great role both in pure and appliedmathematics. Functions that arise during research, properties of which you need tostudy, can be approximated with linear combinations of concerned polynomials. Thus,one may deduce properties of the approximation which is often much easier.
The study of orthogonal polynomials and their properties is a large and interestingbranch of mathematics with great and important applications.
As it often happens in science, a nice construction can be useful in many questions.It turned out that the Jacobi polynomials, or being precise their zeros, gavesolution to a problem that appeared much later that they were invented.
Consider two electric charges of positive quantity q and p fixed along the edgesof the segment $[-1,1]$ and $k$ unit charges randomly placed inside. Unit charges areallowed to move, but not to leave the segment. As all the charges are positive, theytry their best to run away one from another as far as possible. How will they bearranged to minimize potential energy of the system? The problem is to find such aconstruction when all the forces are balanced.
Lets consider first some particular cases.
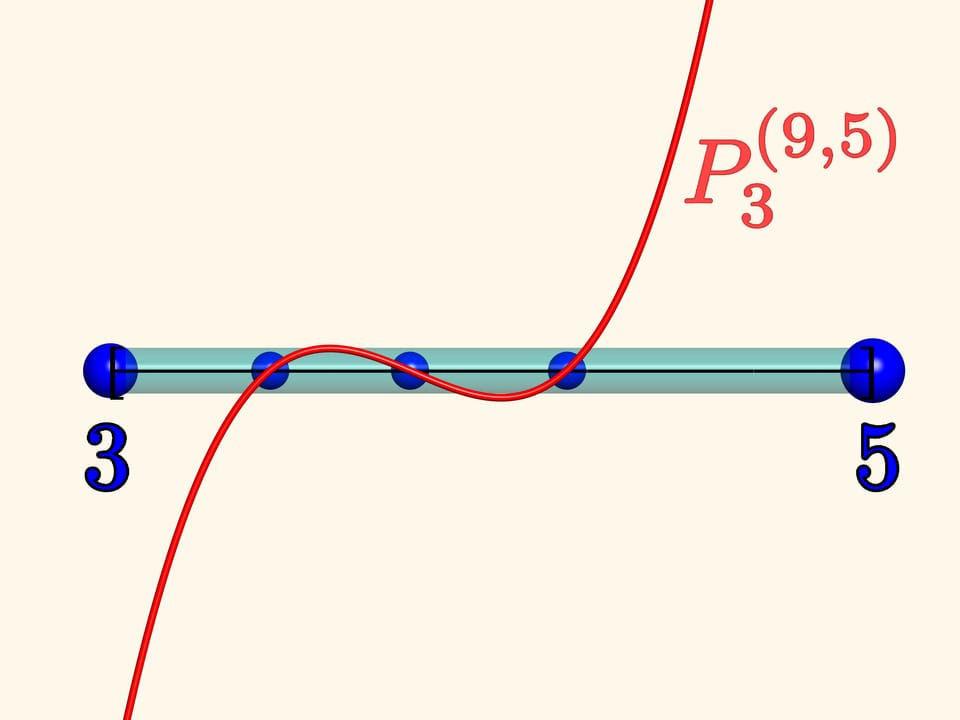
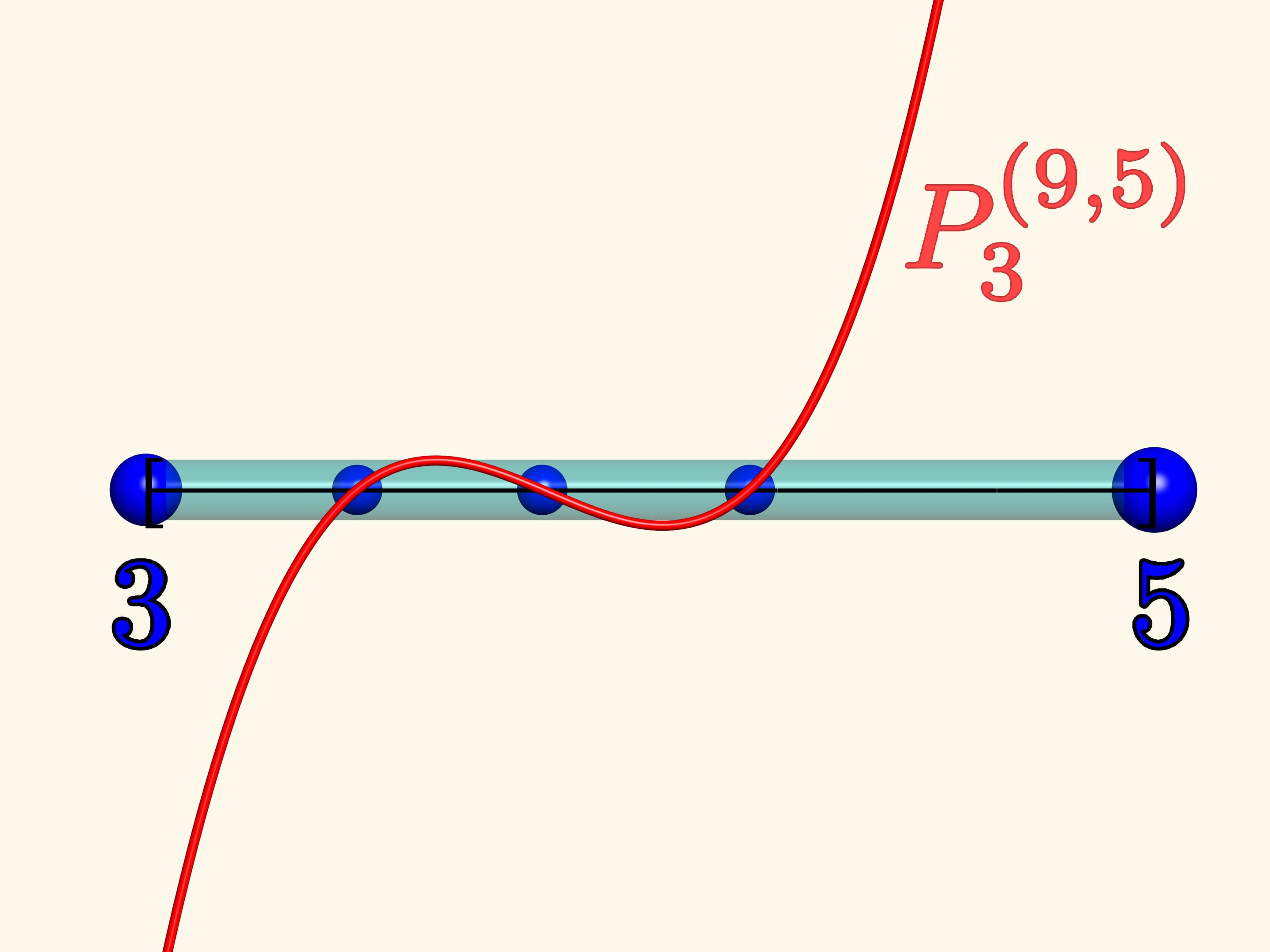
Let the left fixed charge be of quantity 3, and the right of quantity 5. Lets placerandomly three unit charges that can move freely inside the segment and watch themfor a while. When they stop moving, we draw the graph of the Jacobi polynomial $P_{3}^{(9, 5)}$ onthe same segment. It turns out that the charges stopped exactly inthe zeros of this polynomial!
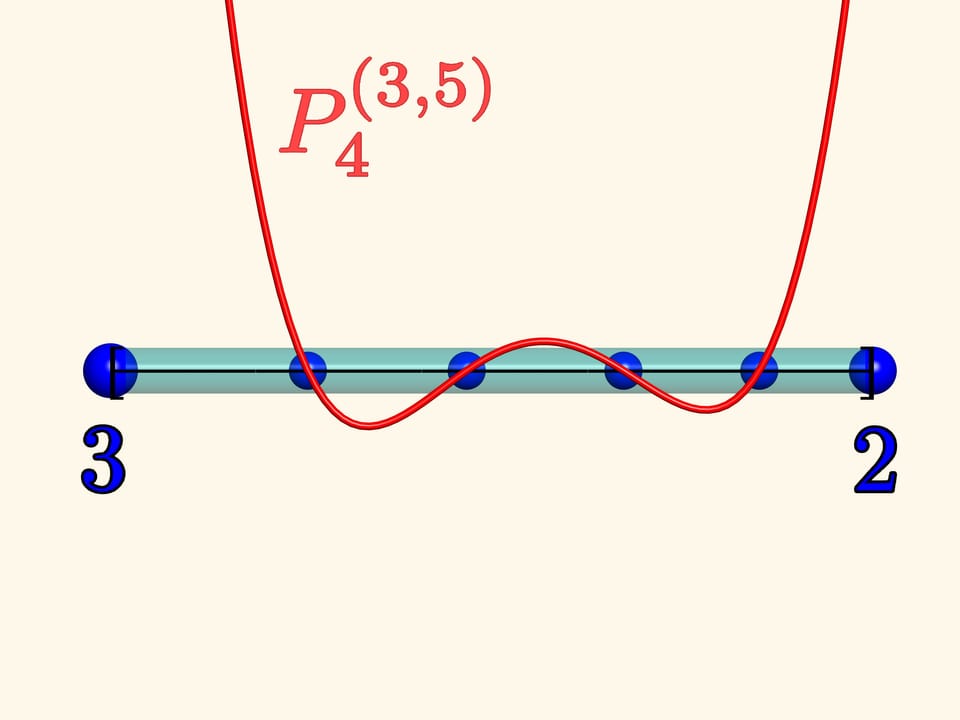
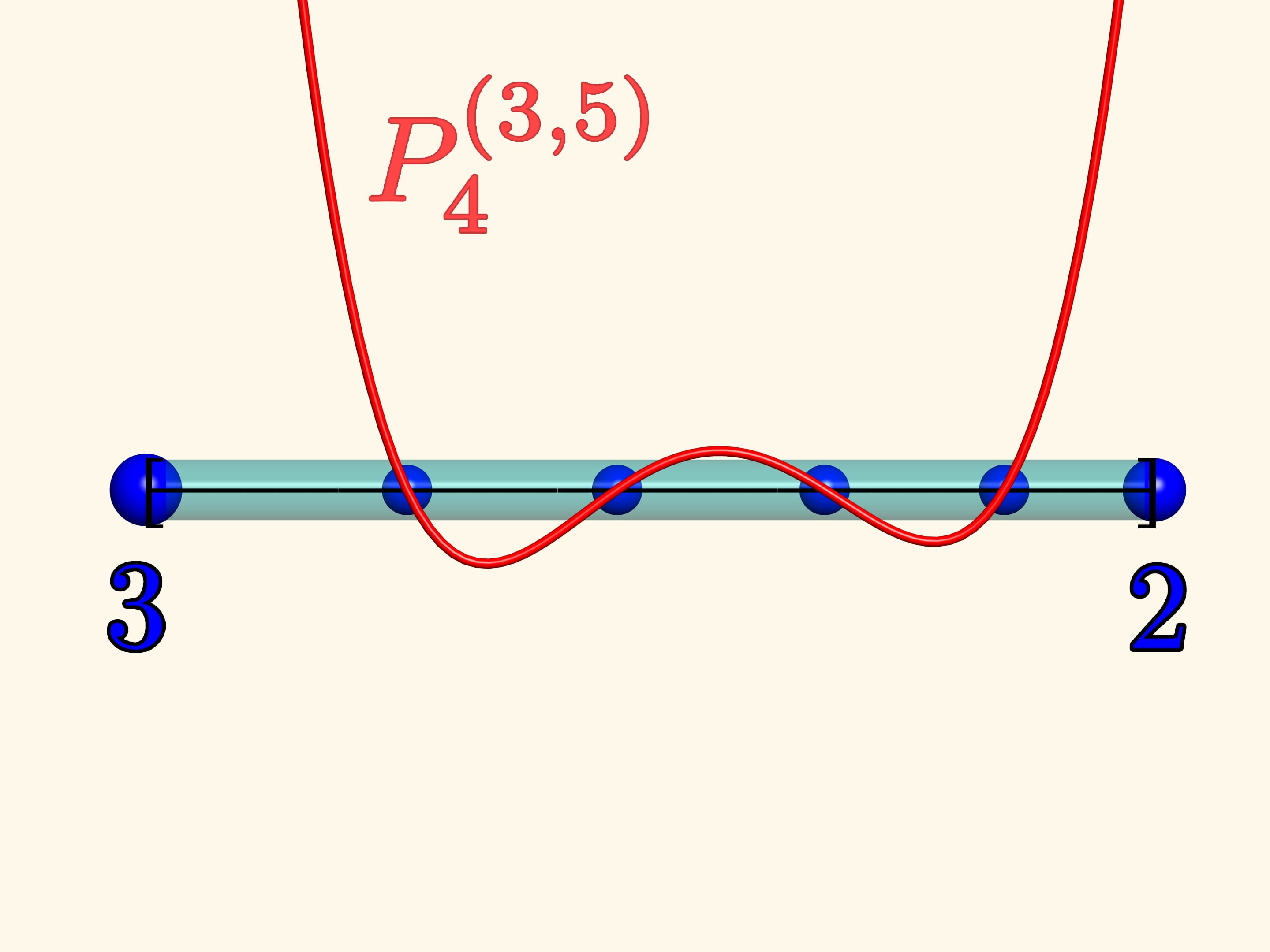
Lets experiment once again. Fix charges of quantity 3 and 2 on the left and the rightedge respectively. We place four unit charges and watch the system. When the stopmoving they will be exactly in the same positions where the zeros of the Jacobipolynomial $P_{4}^{(3, 5)}$ are.
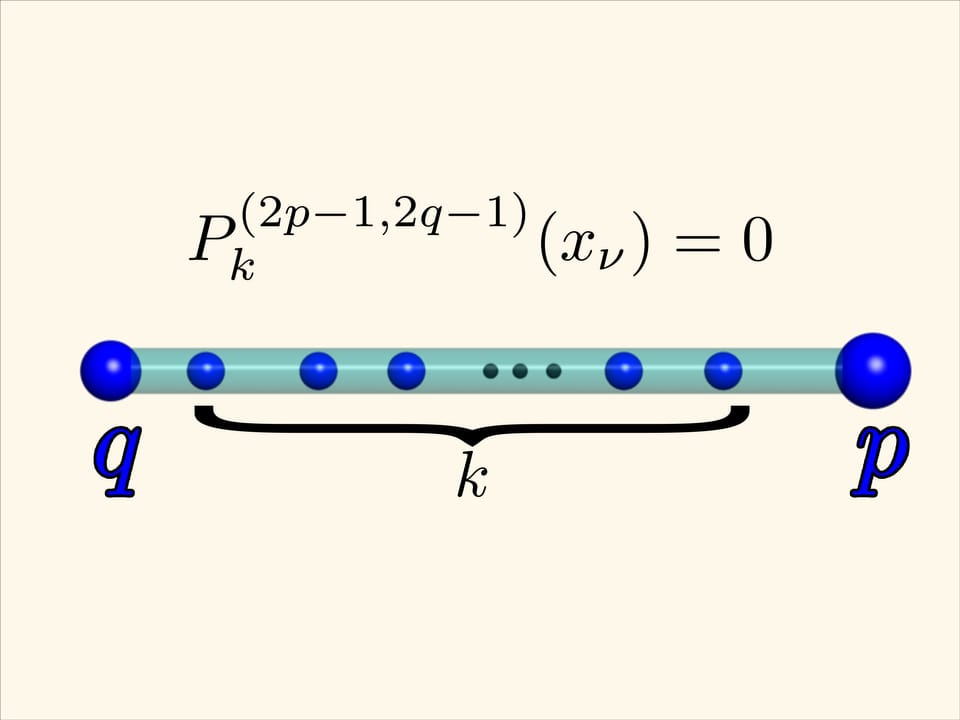
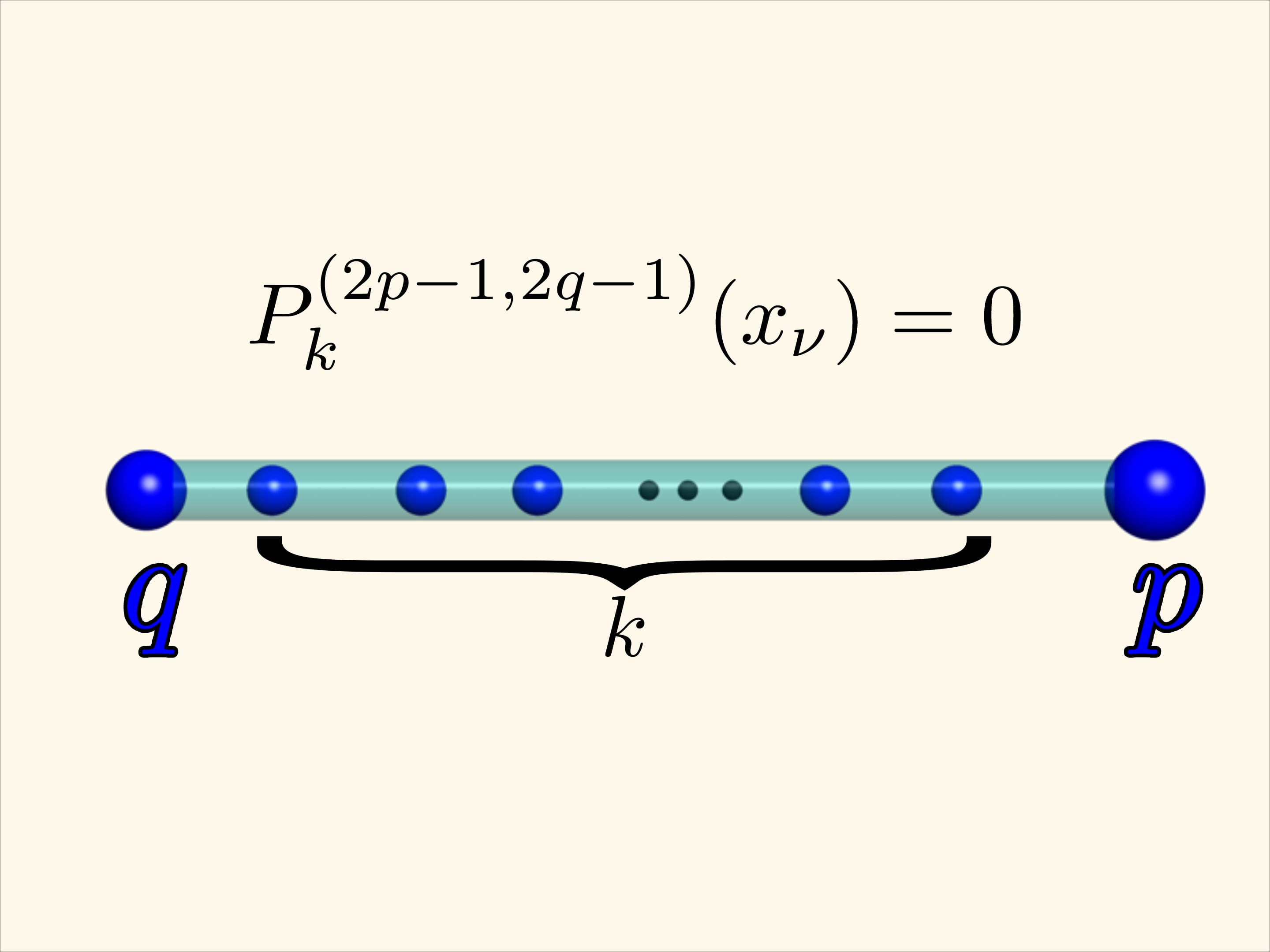
This effect holds in general too. Given electric charges of positive quantity q and p fixed at points -1 and 1 respectively and $k$ unit charges between them, theminimum of potential energy is reached when the «internal» charges are placed in the zeros of the Jacobi polynomial $P_{k}^{(2p-1, 2q-1)}$.
That is how once invented class of orthogonal polynomials appeared while solving aproblem from a completely different scientific area. The Jacobi polynomials also showtheir hidden properties in many other problems as any other «nice construction».