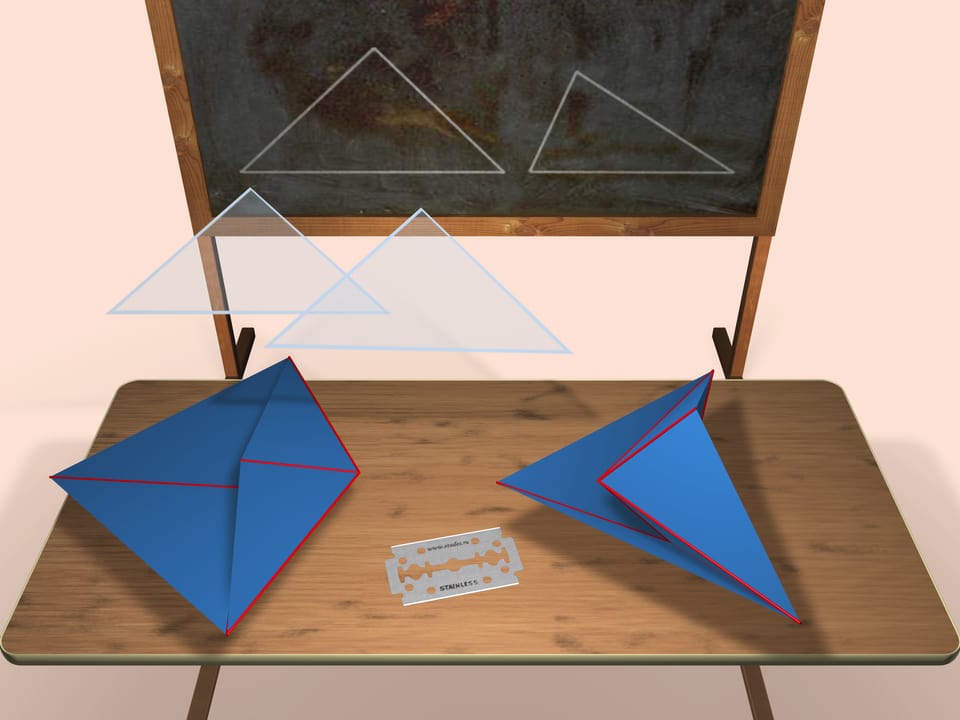
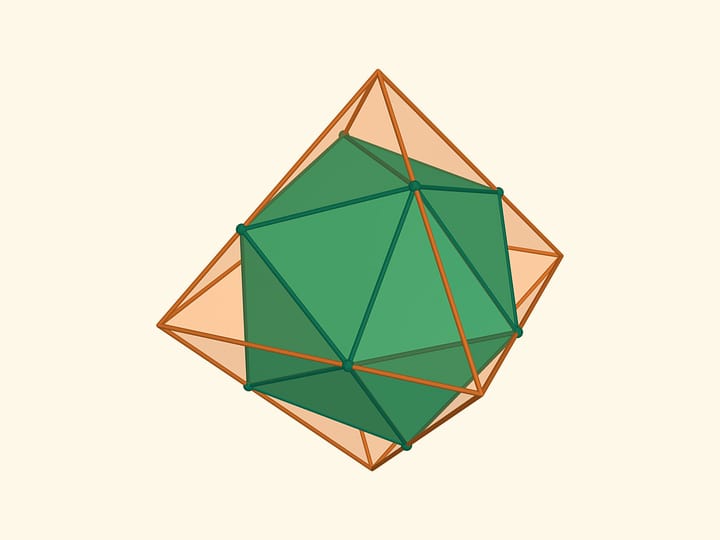
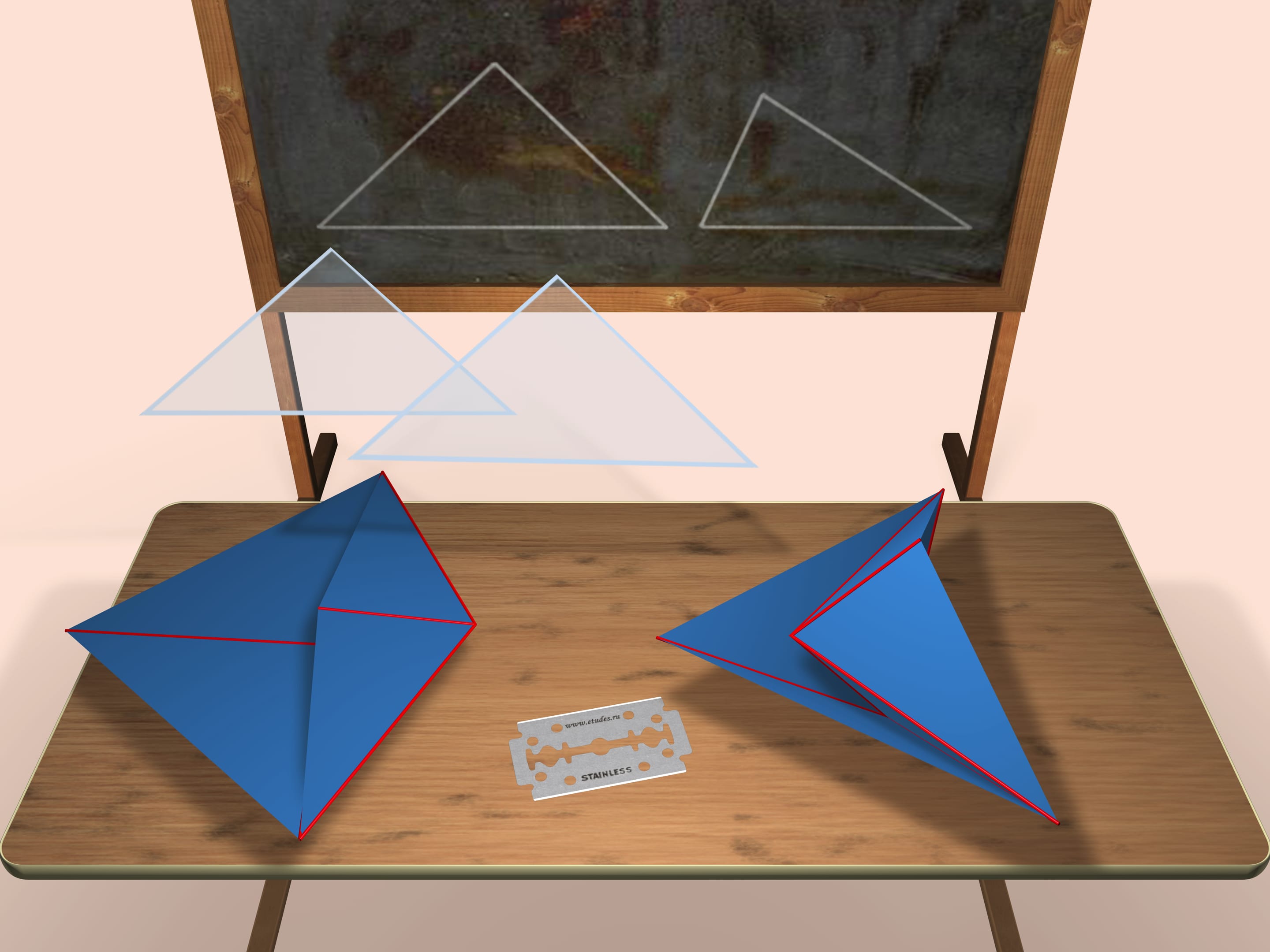
Is it possible to construct both not a convex and a convex polyhedra from the same set of faces? You'd definitely say Yes. One of the examples is presented in the picture.
A polyhedron is called convex if it is placed in a single semi-space with respect to any plane containing one of it's faces.
A polyhedron is not convex if there exists a plane containing one of it's faces that cuts it into two pieces.
Let's assume that we managed to construct a convex and a non-convex polyhedra from the same set of faces. Which of them has the greater volume?
It turns out that we can choose faces, so that the volume of the non-convex polyhedron will be greater that the volume of the convex one having the same faces. In this film we tell about the best example known so far.
Consider two triangles (the accurate length of their edges will be given in the end of the film) that will be faces of our polyhedra. They will be the faces of both polyhedra. The one shown on the left is convex, the one shown on the right is not.
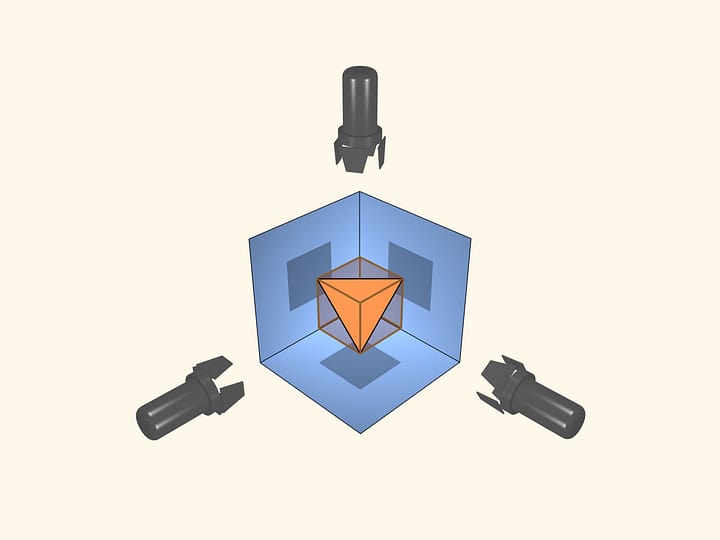
Both constructed polyhedra are octahedra (though, not regular) i.e. they have 6 vertices and 8 faces.
What is an informal meaning of volume, in particular of a polyhedron? It's the amount of liquid that one can pour into it. Let’s cut off the vertices and start to already filled whereas the nonconvex one — not yet. But maybe the speed of water was different: to measure the amount of water properly, let's pour out the water from each polyhedron to identical is higher than in the left one. This means that the volume of the nonconvex polyhedron is really greater than the volume of the convex one.
If you calculate precisely you will get that the ratio of the volume of nonconvex polyhedron to that of the convex is 1,163.
In our problem it's more correct to consider the ratio of volumes than it's difference as it doesn't depend on the size of initial triangles used to construct polyhedra.
The volume of the constructed non-convex polyhedron is more then 16% greater than those of the convex one. You can make this polyhedra yourself using faces with the given edges. If you place the centers of octahedra in the origin, their vertices will have the same [coordinates] coordinates as in the film.
We considered here an example constructed by S. N. Mikhalev while he was a Ph.D. student in MSU. It's the best known example so far (it has the greatest ratio of polyhedra volumes).
However, it is still non known how big can the ratio of volumes of such two polyhedra be (of a non-convex and a convex one constructed from the same set of faces). And this problem is waiting for it's researcher!