Snell’s Law ⁠

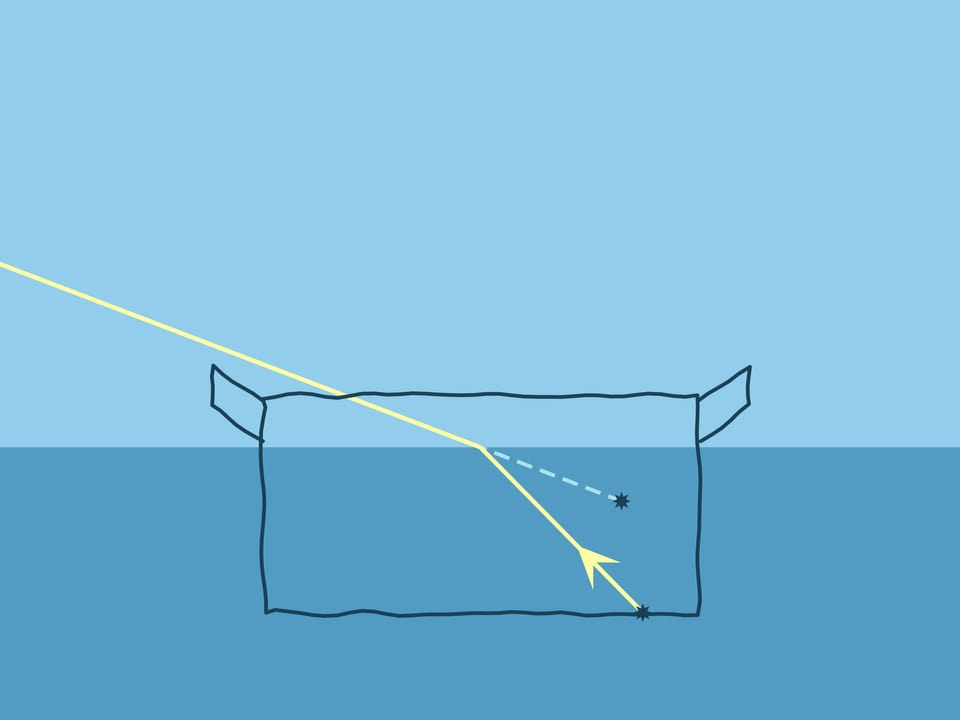
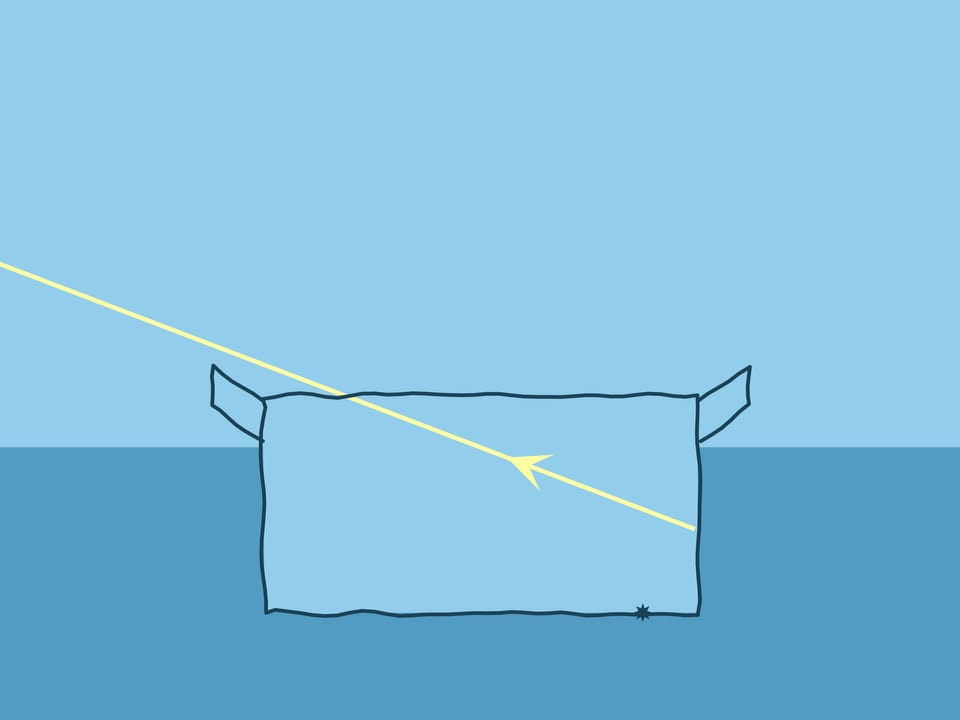
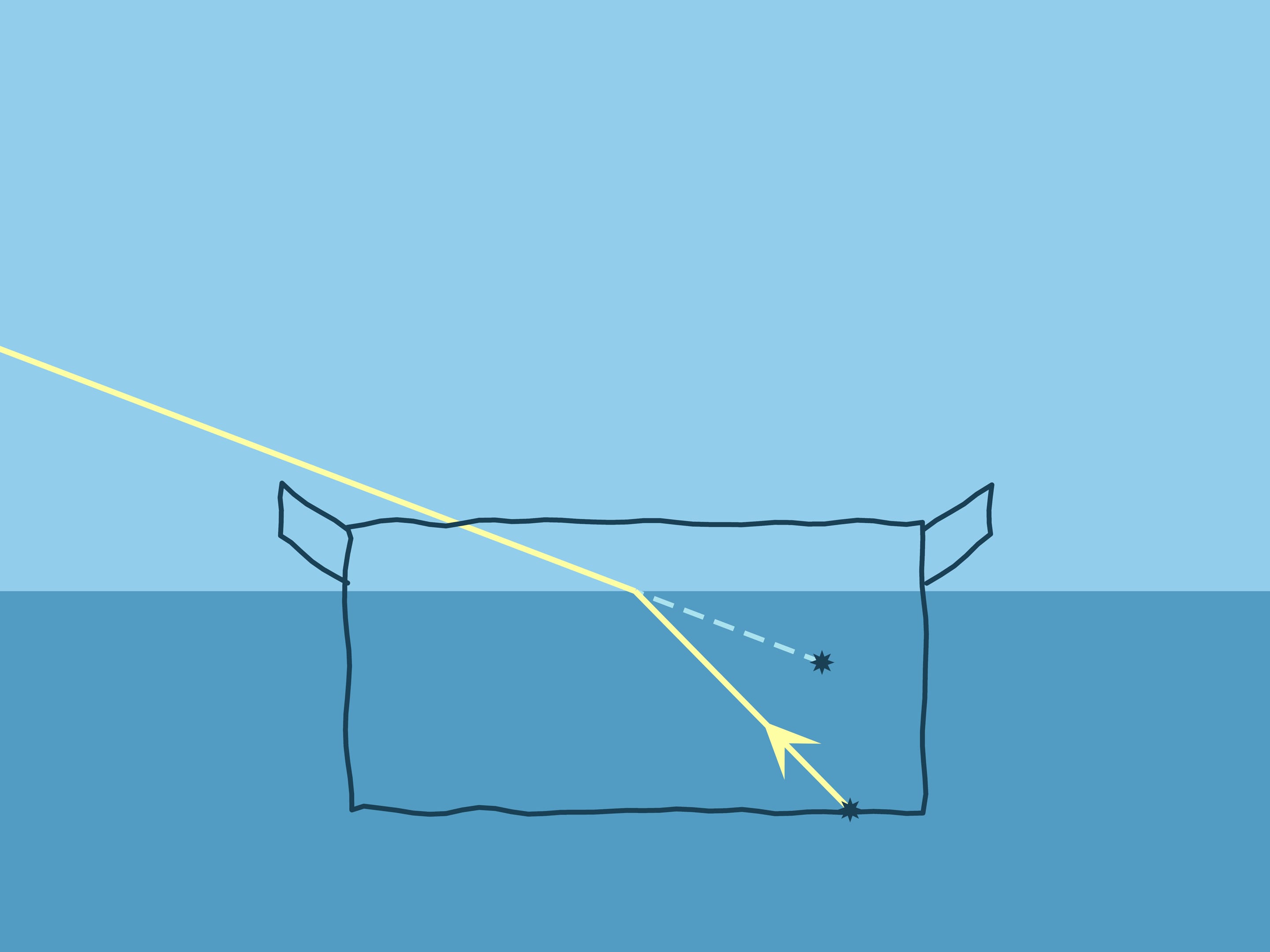
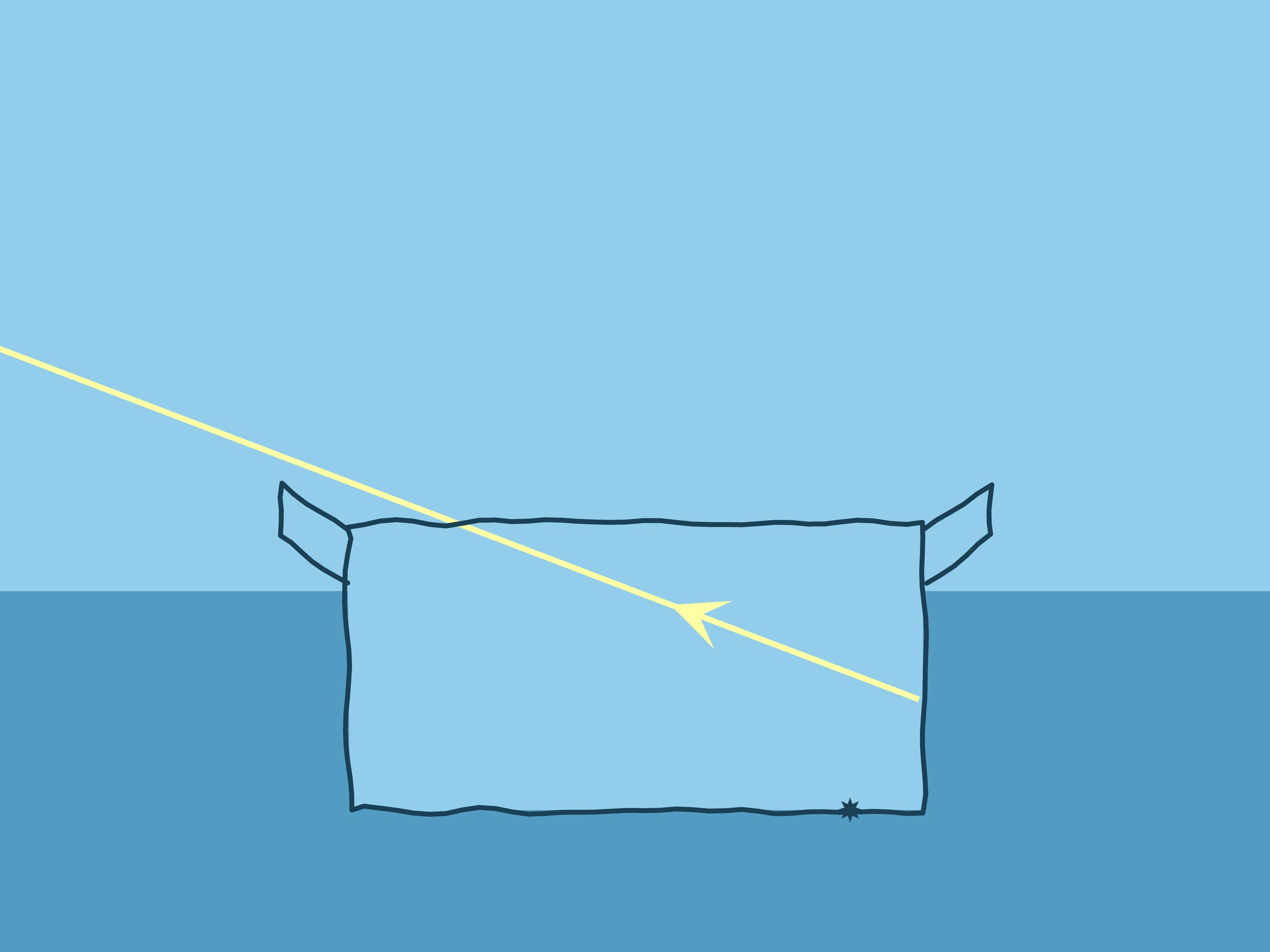
Which pot seems to be deeper, the empty one or filled with water? Do an exper­i­ment — take a pot, put a coin on the bottom to make it clearer, posi­tion the pot so that the coin is out of sight, and keeping the pot still, start pouring water…

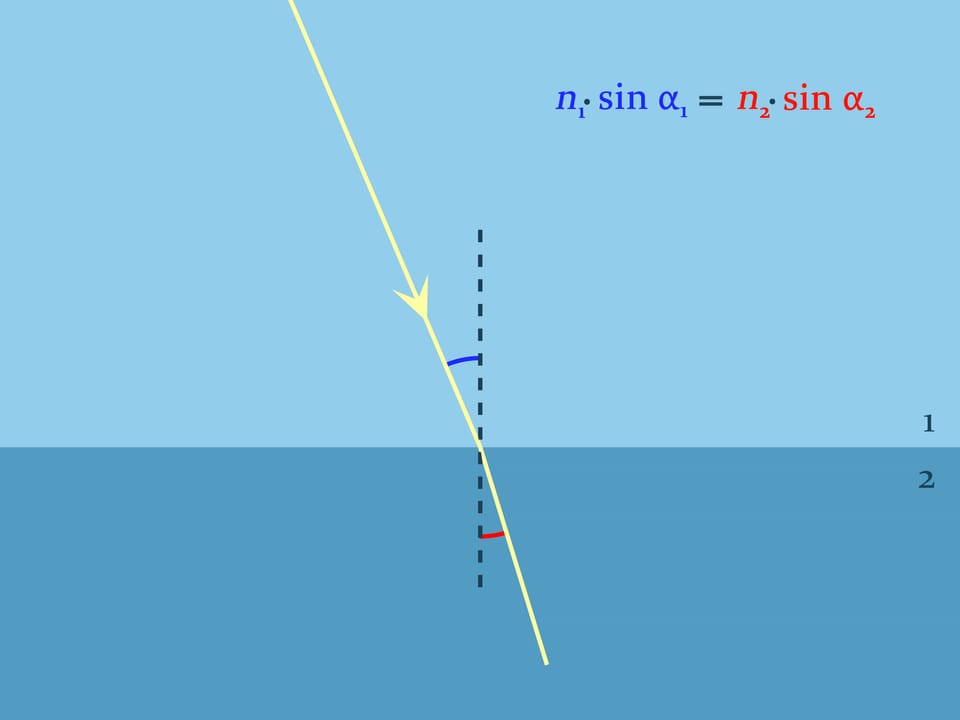
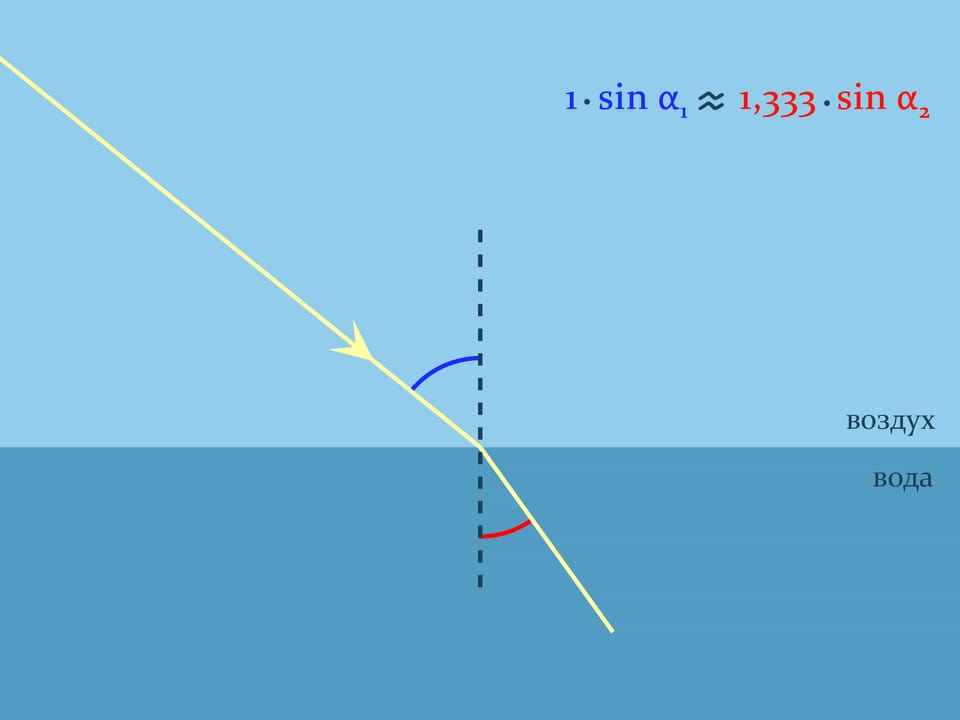
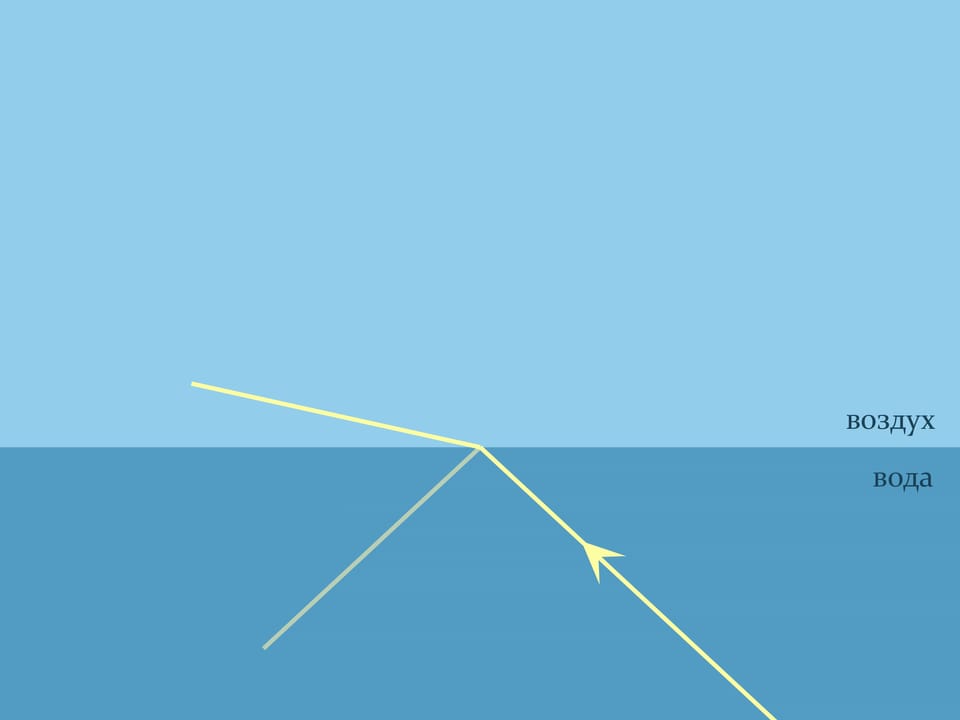
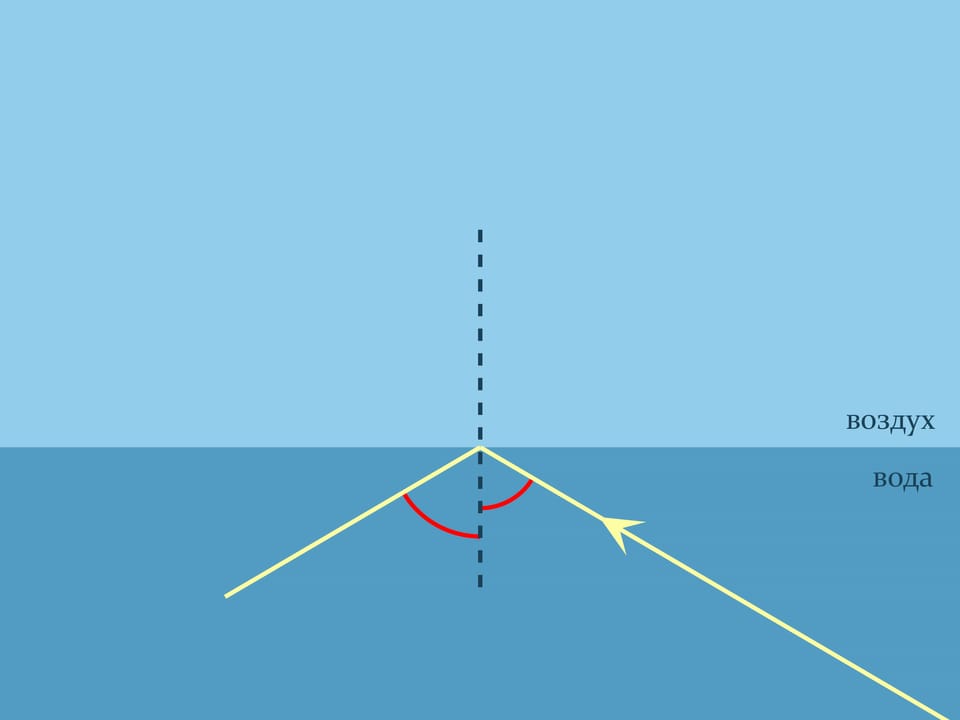
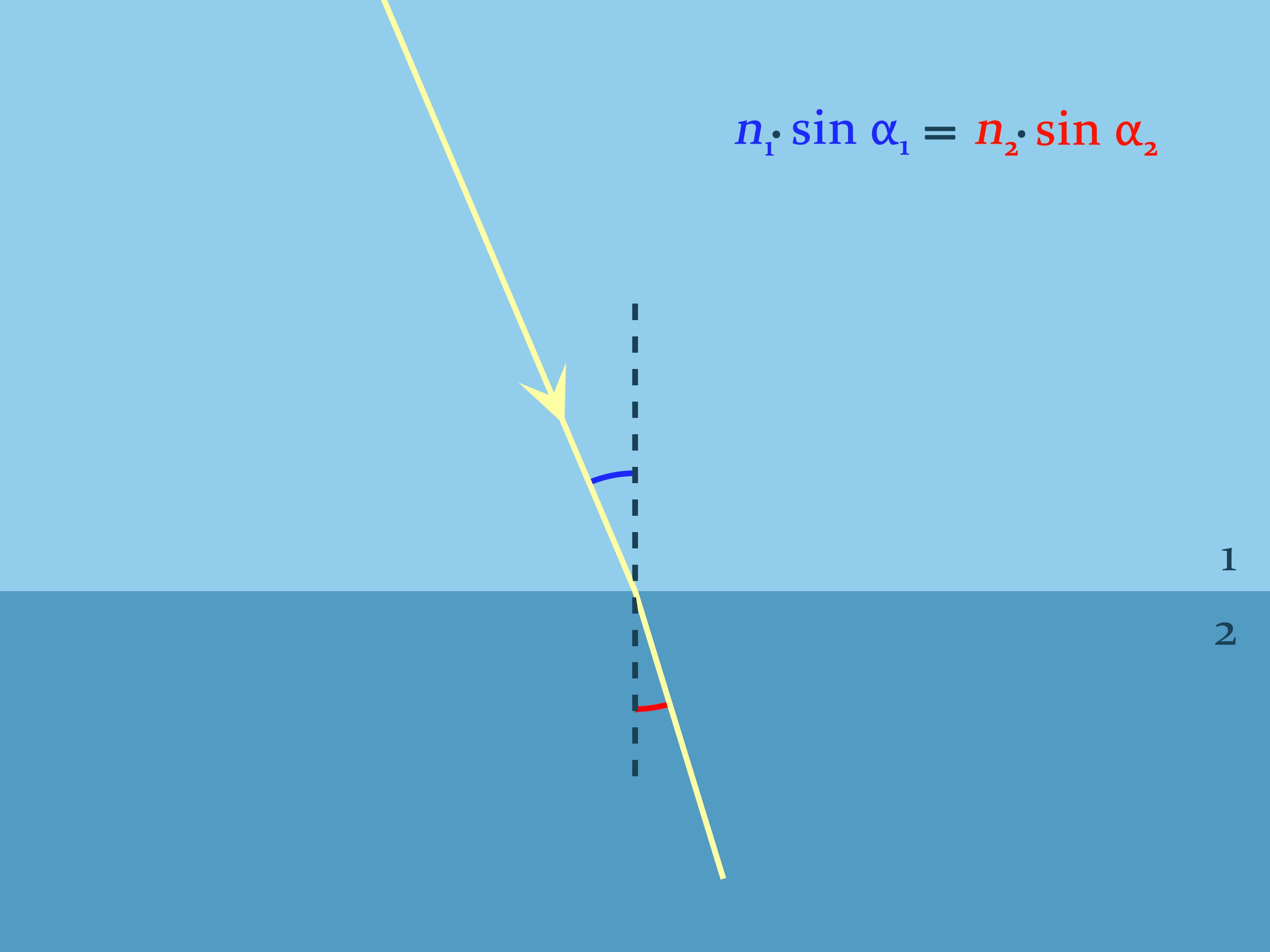
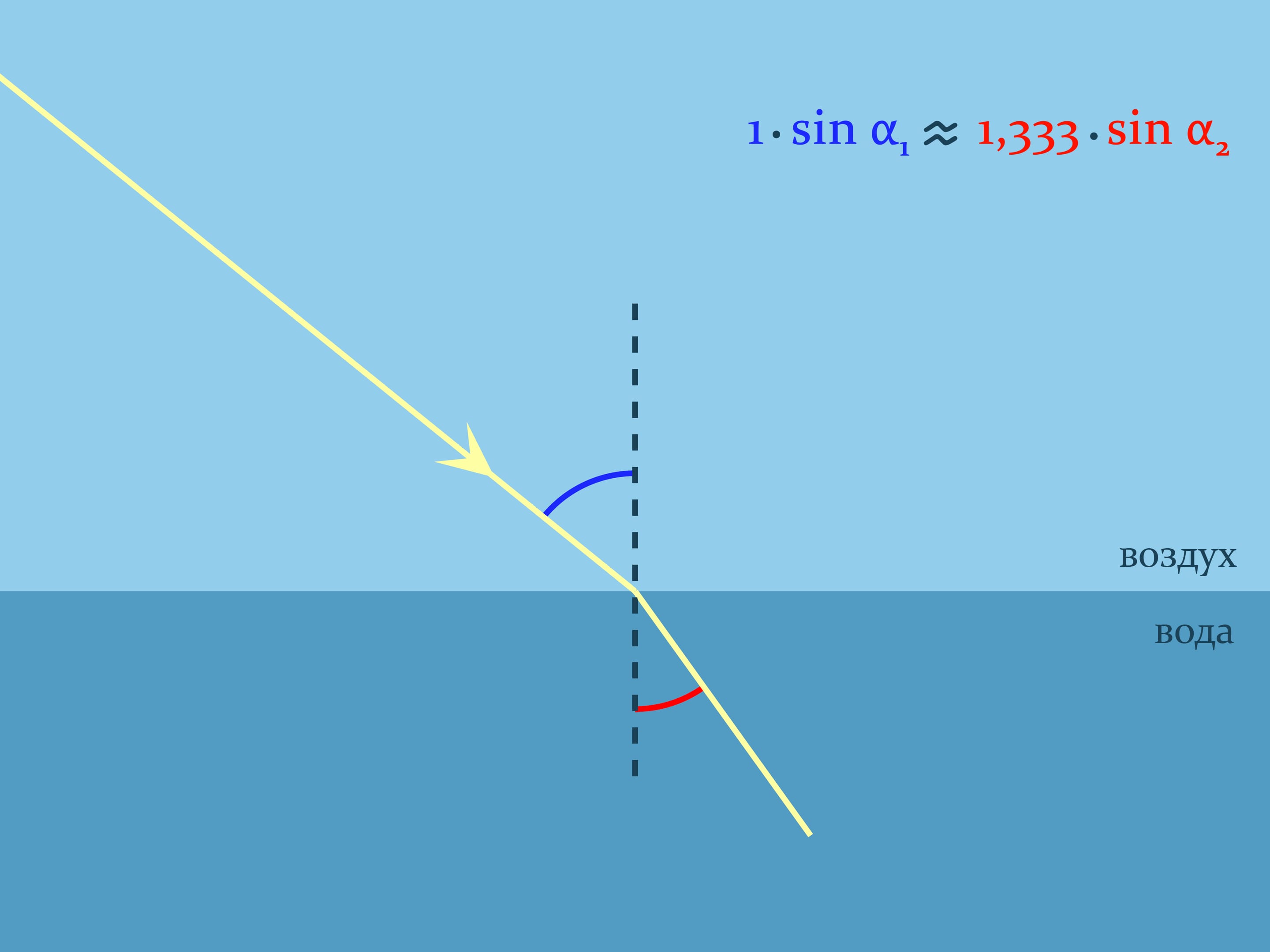
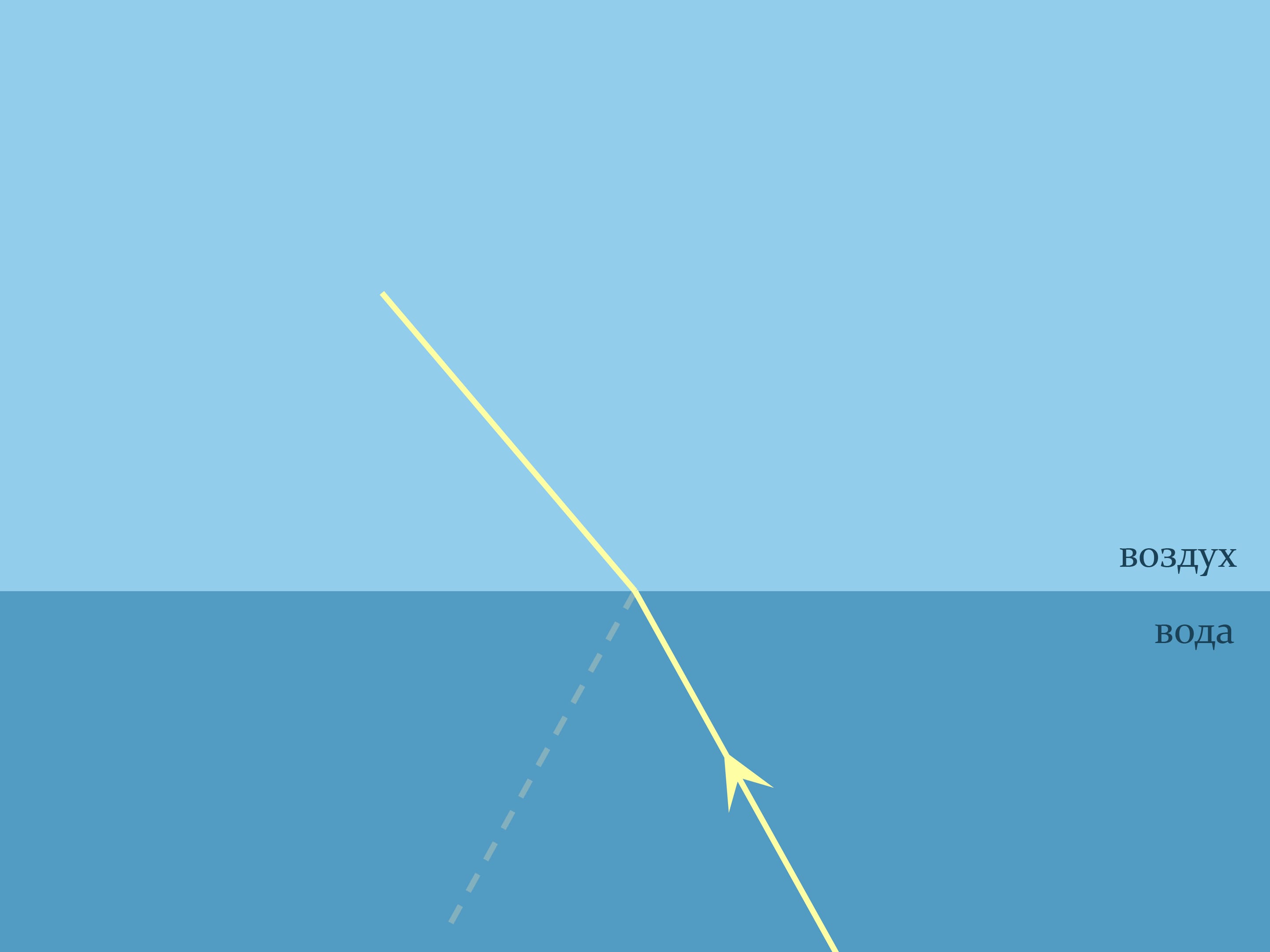
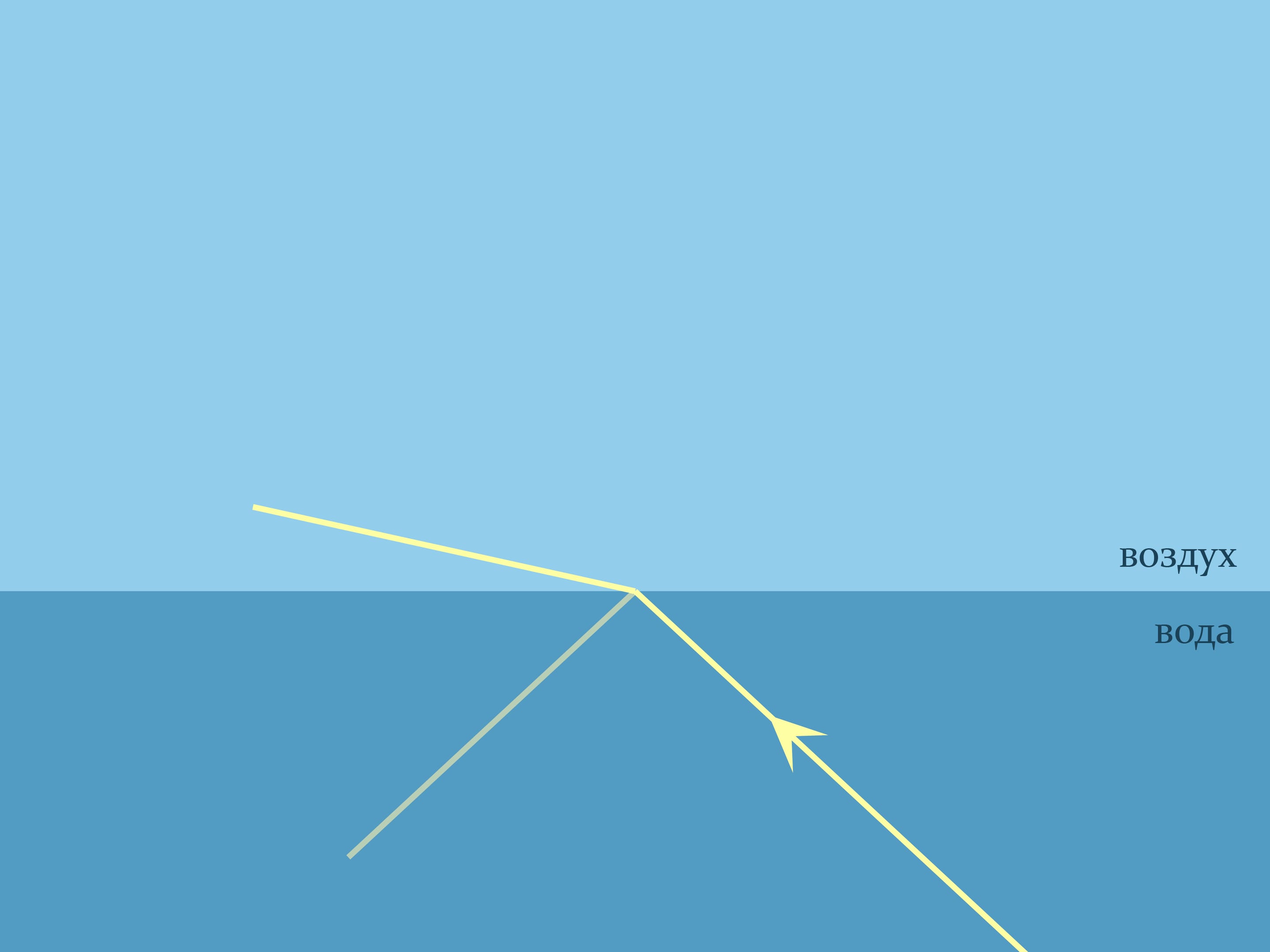
The refrac­tion law of light of geometric optics, named after the Dutch math­e­mati­cian, physi­cist and astronomer W. Snell, helps to substan­tiate what you see. It explains how light is refracted when it passes between two opti­cally diver­gent media. Snell’s law states how refrac­tion will occur: $n_1\sin\alpha_1= n_2\sin\alpha_2$, where $n_1$ and $n_2$ are the refrac­tive indices of the media, describing how many times the speed of light in the medium is lower than the speed of light in a vacuum, and the angles are counted from the normal to the boundary. For the air the refrac­tive index is nearly equal to $1$, and, for example, for the water at room temper­a­ture $n\approx1{,}333$.

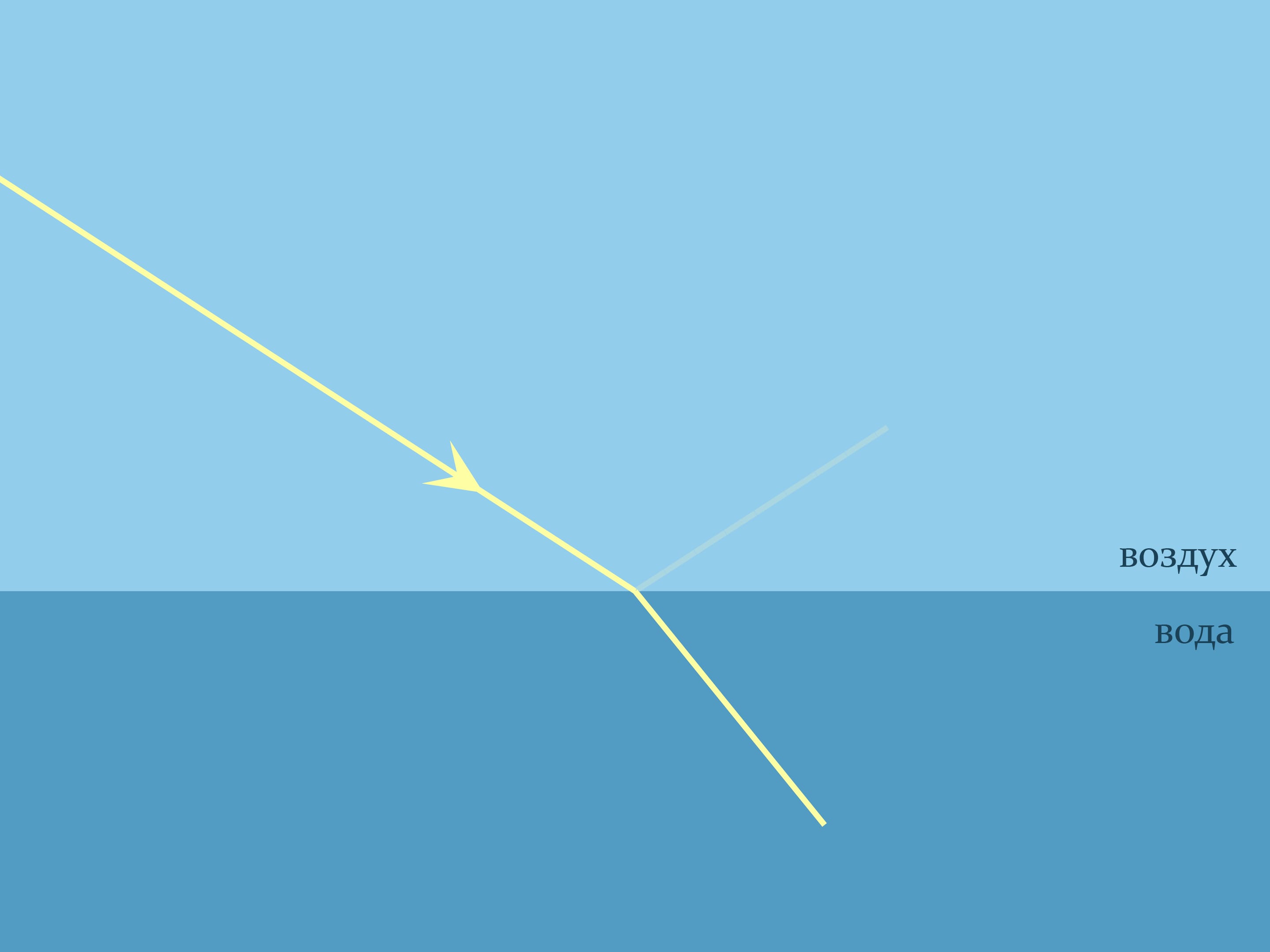
It seems that both the picture and the formula are symmetric — if the ray in water is emitted, it should travel along the same path as the ray coming from the air. But that is not always true.

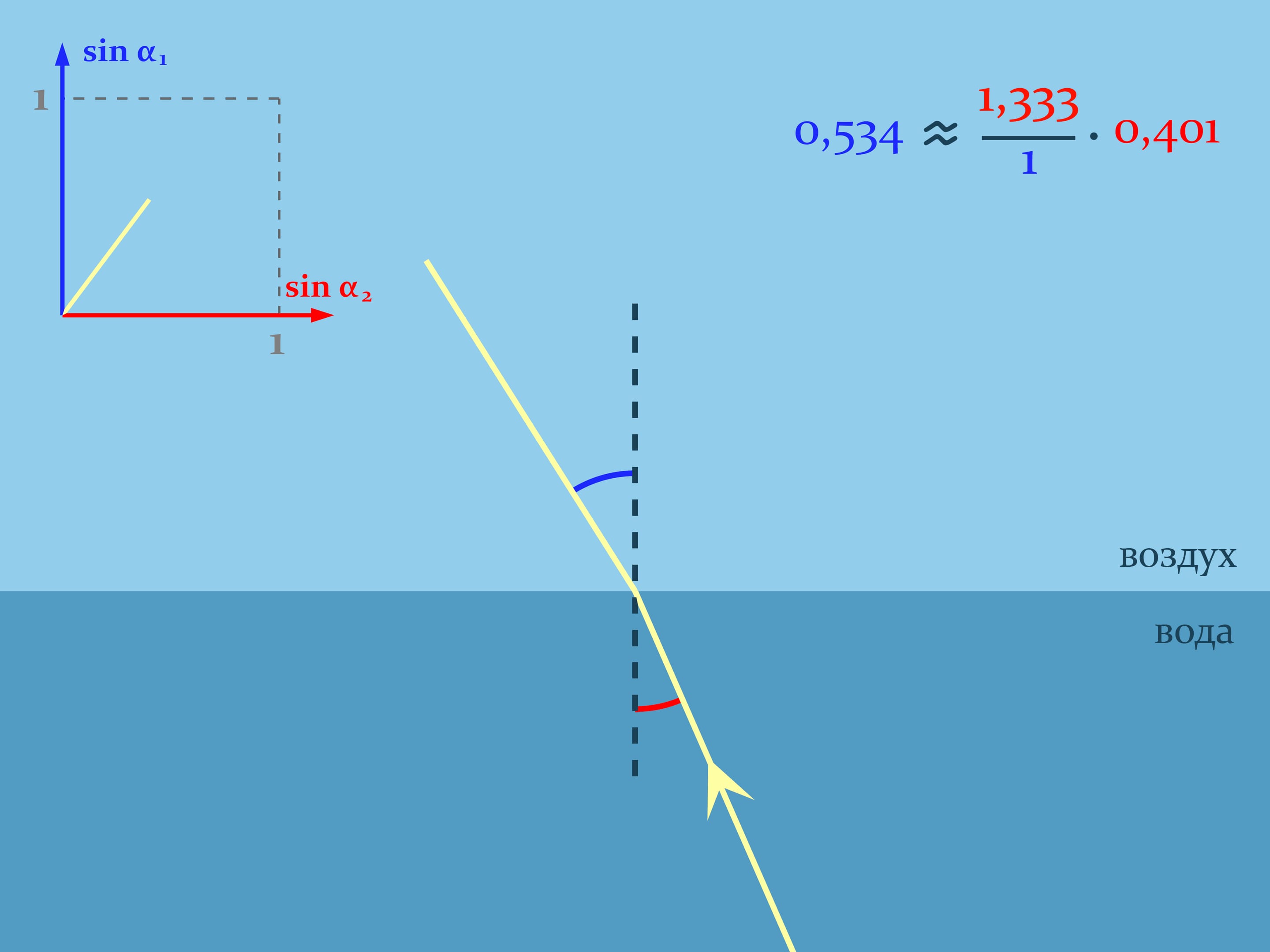
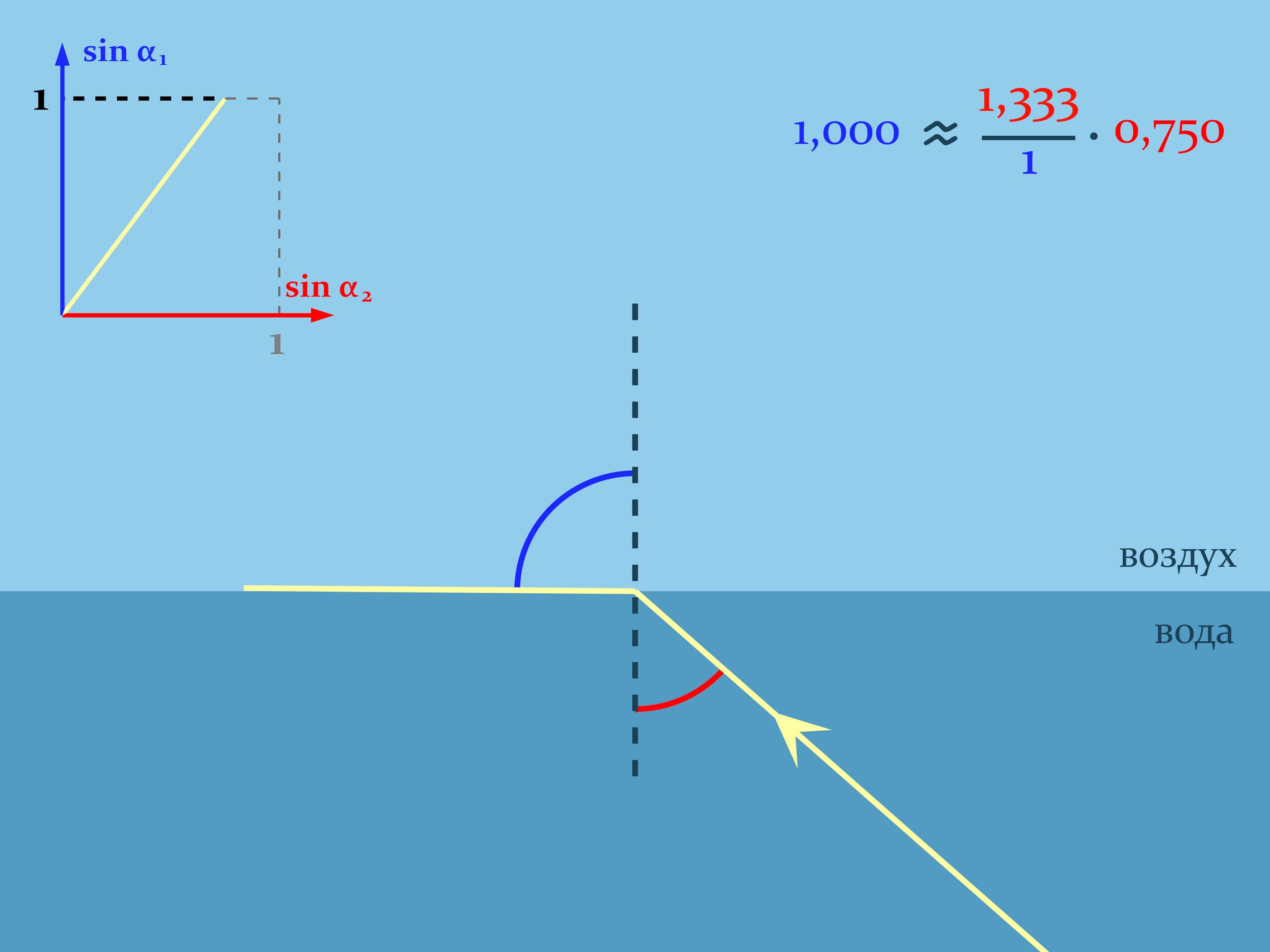
Let the ray out of water and watch the graph of the func­tion that links the sines of the angles: $\sin\alpha_2=\frac{n_1}{n_2}\sin\alpha_1$. When the sine of the angle in water will be $\approx 3/4$, an exit angle of the ray in the air will be $90^\circ$, and conse­quently, its sine will be equal to one. And the sine of the angle in water will be $0{,}75$ and continue to increase. What would happen if we continue to increase the angle between the normal and the ray in water? A more compre­hen­sive analysis of the ray passage through the media boundary will help to explain it.

When a beam hits the border of two media, both refrac­tion (according to Snell’s law) and reflec­tion (according to the law the angle of inci­dence equals the angle of reflec­tion) always occur. The direc­tion where most of the beam goes depends on the angle. And when the ray approaches almost parallel to the boundary from the opti­cally more dense side, a total internal reflec­tion takes place — the whole ray is reflected from the less dense medium like from a mirror.

Having consid­ered Snell’s law at all possible angles of the beam and the normal, let us return to the exper­i­ment with the pot. If water is poured, the coin “rises”: if there were no water, the observer would see the wall of the pot at this angle.

The total internal reflec­tion prin­ciple is at the heart of optical fibre, which is used for trans­mit­ting signals. The opti­cally denser core is surrounded by a less dense shell. A ray emitted into the core at a small angle to its axis is completely reflected from the shell and cannot leave the core: it goes where the optical fibre directs it.

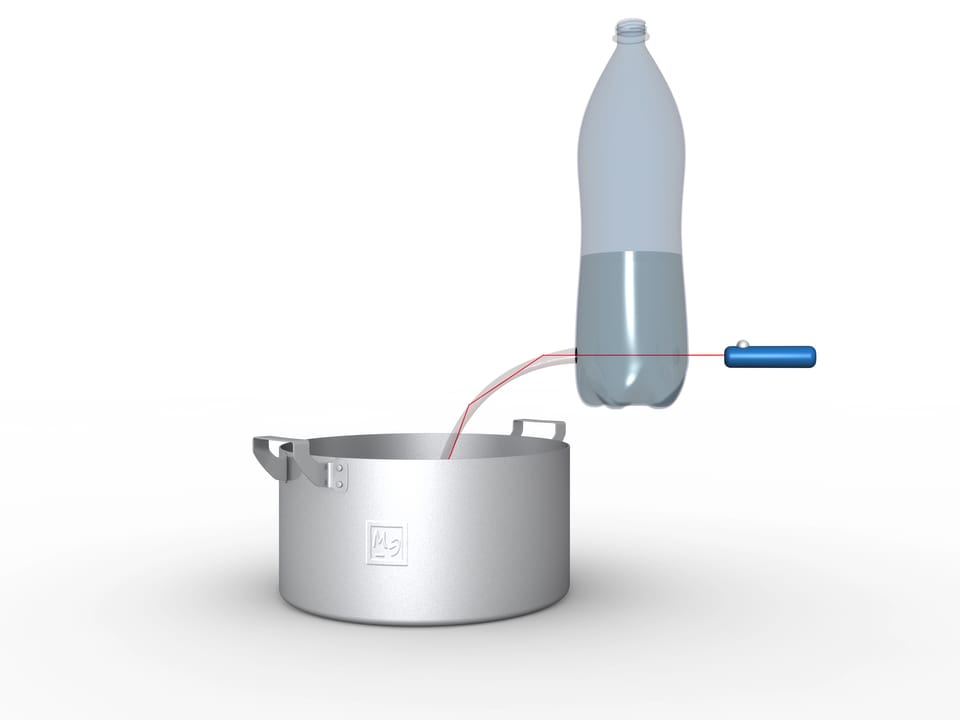
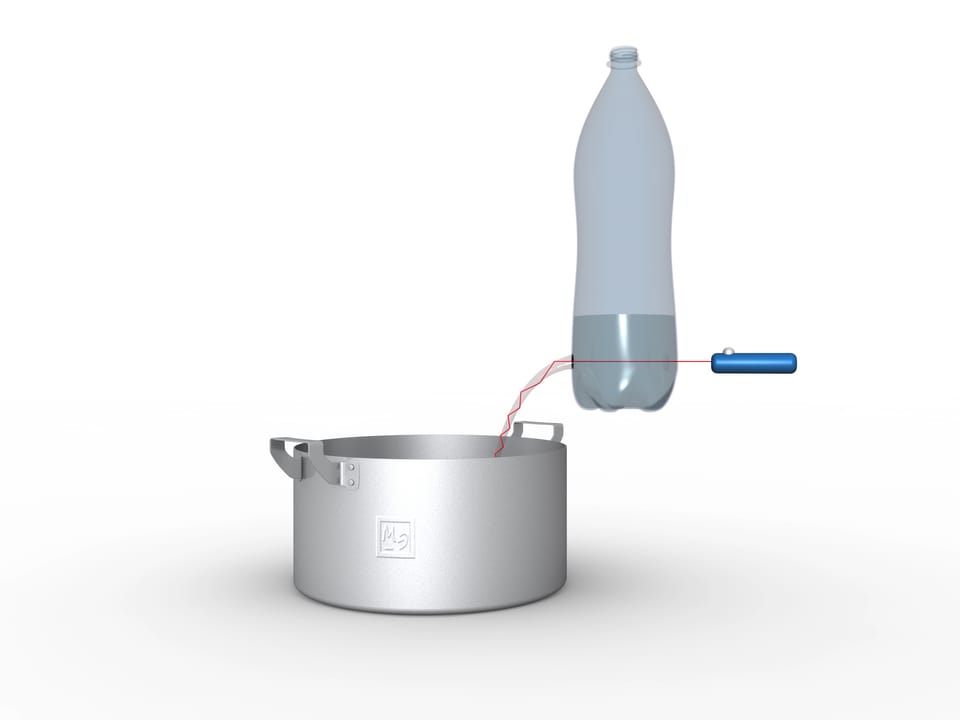
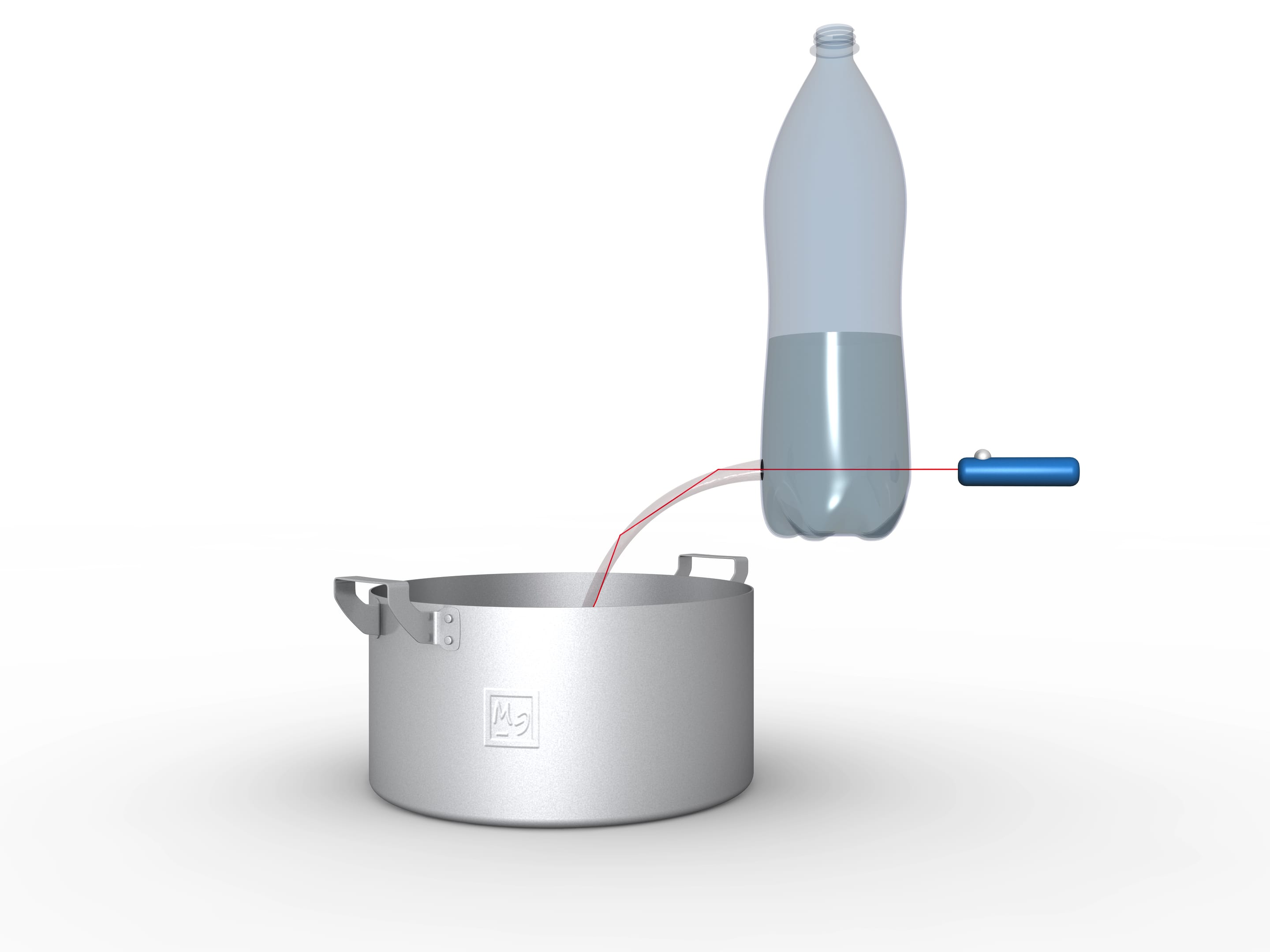
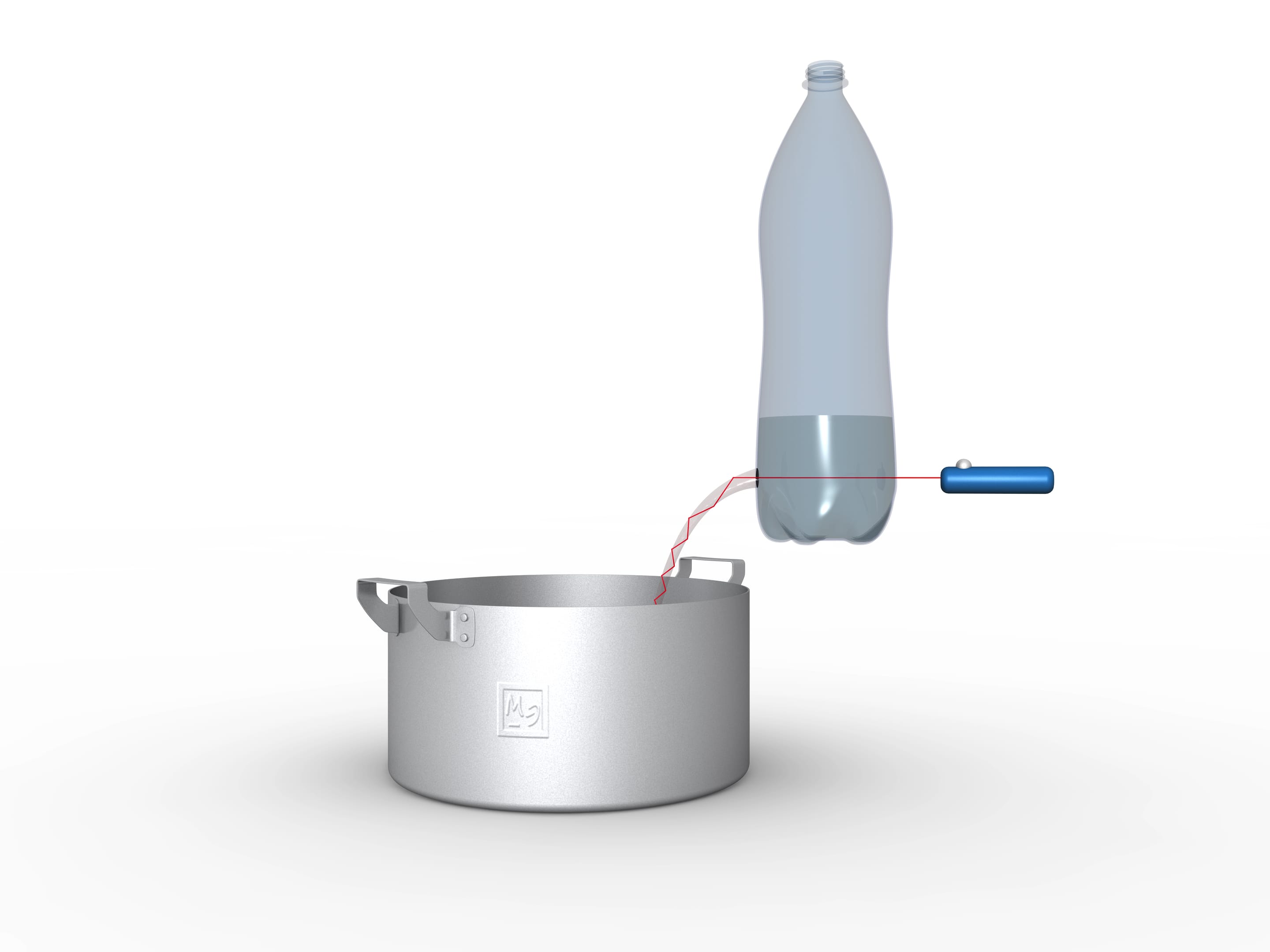
It is not diffi­cult to make a working light tube at home. Make a round hole in the bottom of a clear plastic bottle, pour water in, and direct the laser pointer ray into the flowing stream. You’ll see the glowing poly­line follows the changing shape of the stream. If you add a little color to the water, not only will the stream glow, but the water inside the pot or sink will glow as well.