Drawing an ellipse with a thread provides a way to construct a confocal ellipses and “gives” curious facts about the life of these curves.
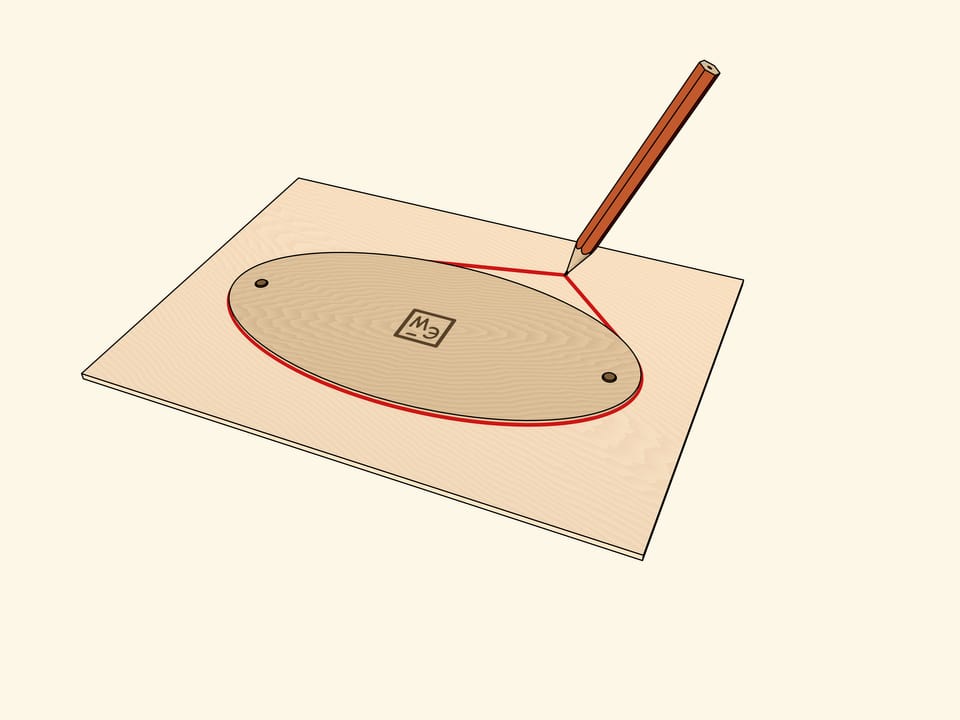
By taking a thread with tied ends which enclosing foci and stretching it with a pencil, draw an ellipse. Threads of different lengths give a whole family of confocal ellipses. But it is possible to enclose one of the already obtained ellipses instead of the segment connecting the foci.
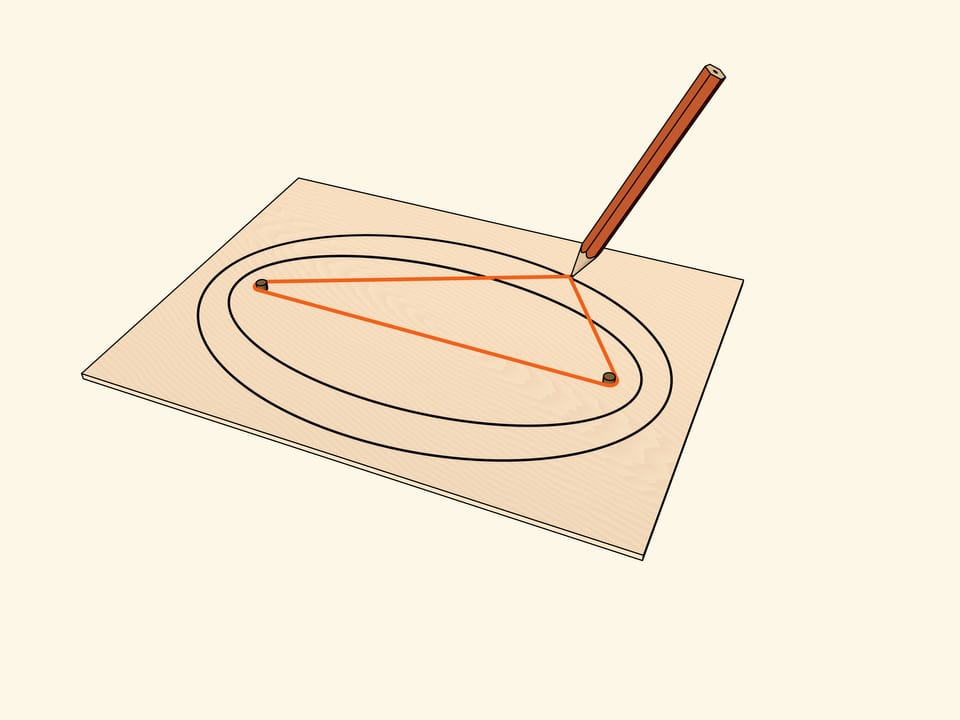
Having drawn the ellipse, let’s make it’s “hard” copy out of a thick enough material, and then align the copy with the original. Then we take a thread loop, which encloses the ellipse, and, pulling it with a pencil, draw an oval line. It turns out that this line is also an ellipse, confocal with the original one. The statement can be verified experimentally by choosing the length of the loop that encloses the foci.
This theorem was proved in the XIX century by the Charles Graves, an Irish bishop and mathematician. In Felix Klein’s book “Lectures on higher geometry” (German: Vorlesungen Über Höhere Geometrie) one of the paragraphs is called “Thread constructions by Graves and Staude” (German: Fadenkonstruktionen von Graves und Staude).
The proof of Graves’ theorem by methods of differential geometry can be found in Klein’s book. Note that it is not elementary, the reason is that at each moment the thread as a line consists of two segments tangent to the ellipse and an arc of the ellipse. Surprisingly, the arc of an ellipse is a very complex object, its length is defined by a complex formula (so-called elliptic integrals are being used). And all we did was squeezing a circle, of which everything is known!
The “physical” proof of Graves’ theorem, based on the intuitive assertion that the tension forces of straight sections of a thread are equal, is known. But whether there is a proof at the level of elementary geometry — without the use of limits and derivatives — is still unknown, and many geometers are still trying to find it.