A one-sheeted hyperboloid of rotation — is a surface, formed by a rotation of a hyperbola around its virtual axis (axis of symmetry, perpendicular to a segment with ends in focuses).
There are two straight lines, which fully lie on a hyperboloid and go through every point of it. Each of them сovers all the surface during a rotation around the axis of a hyperboloid. Consequently, a one-axis hyperboloid can be received by rotation of a straight line around an axis, crossing to it.
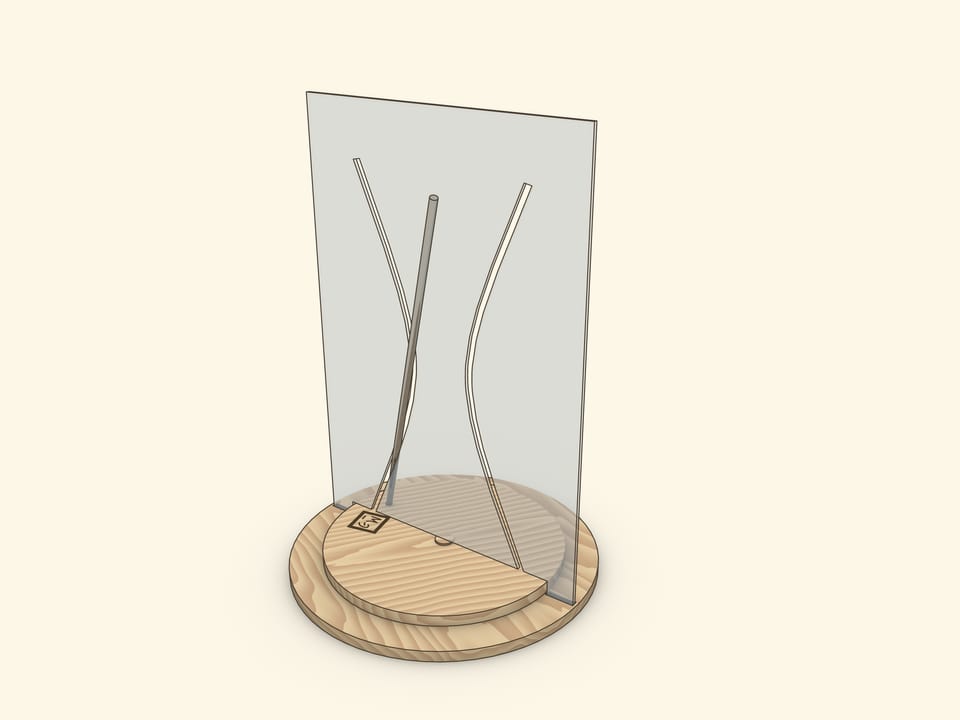
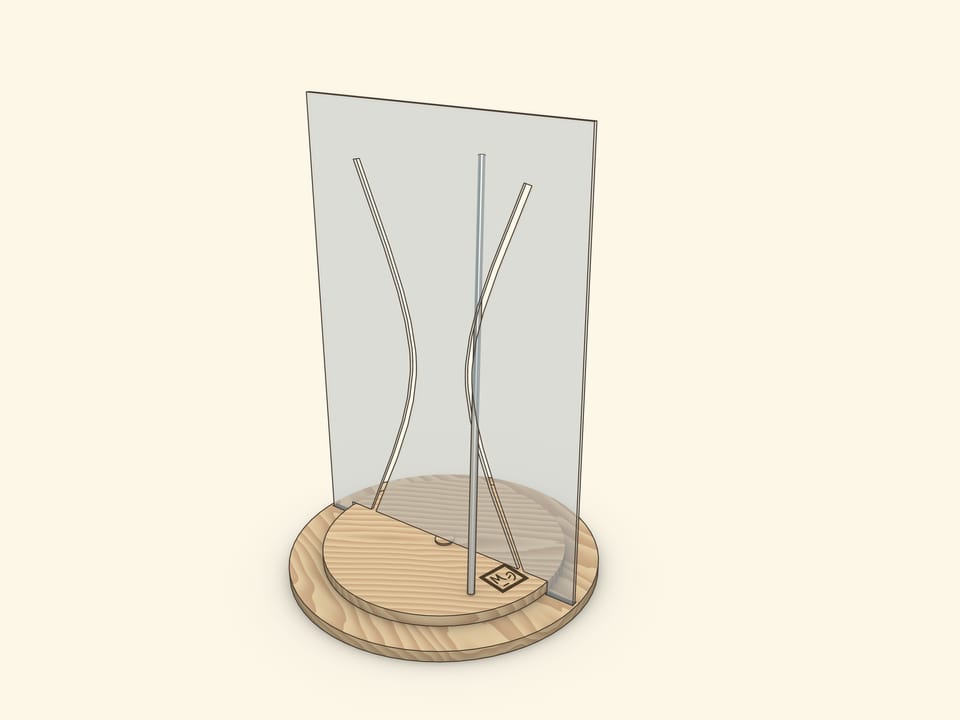
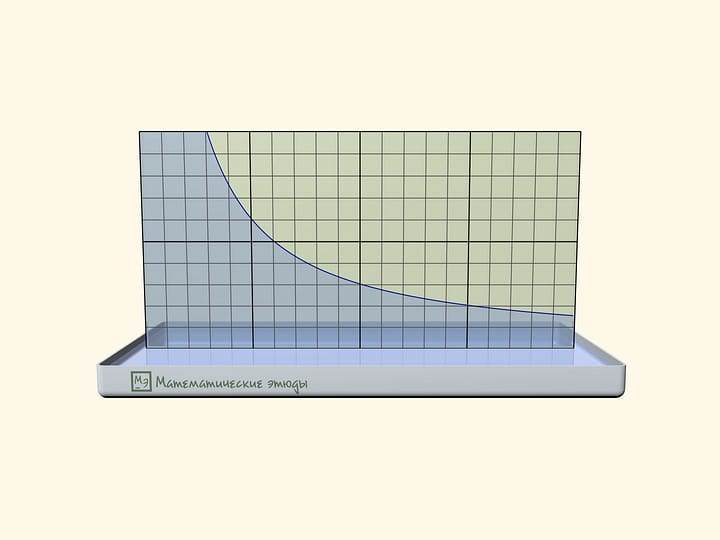
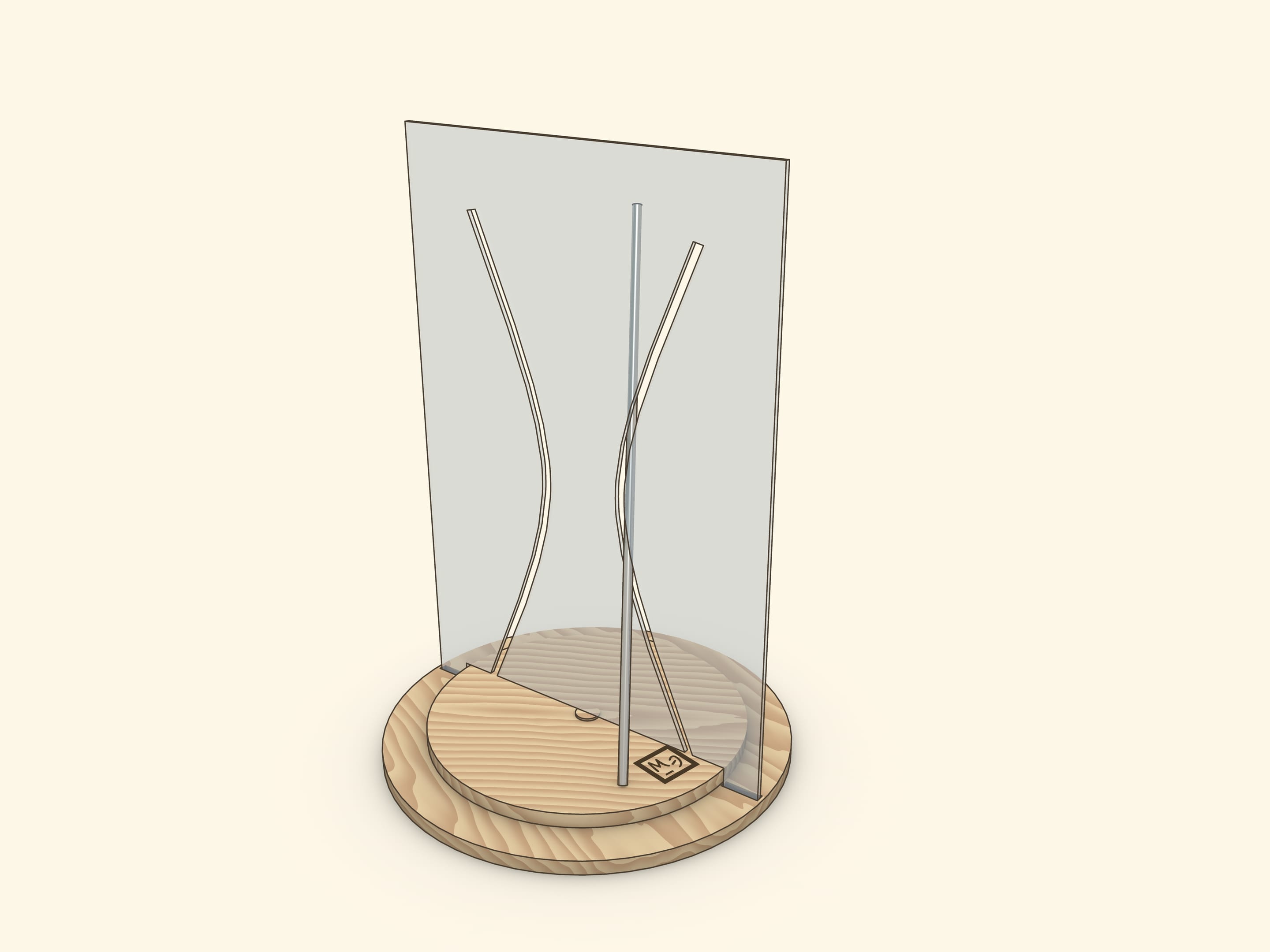
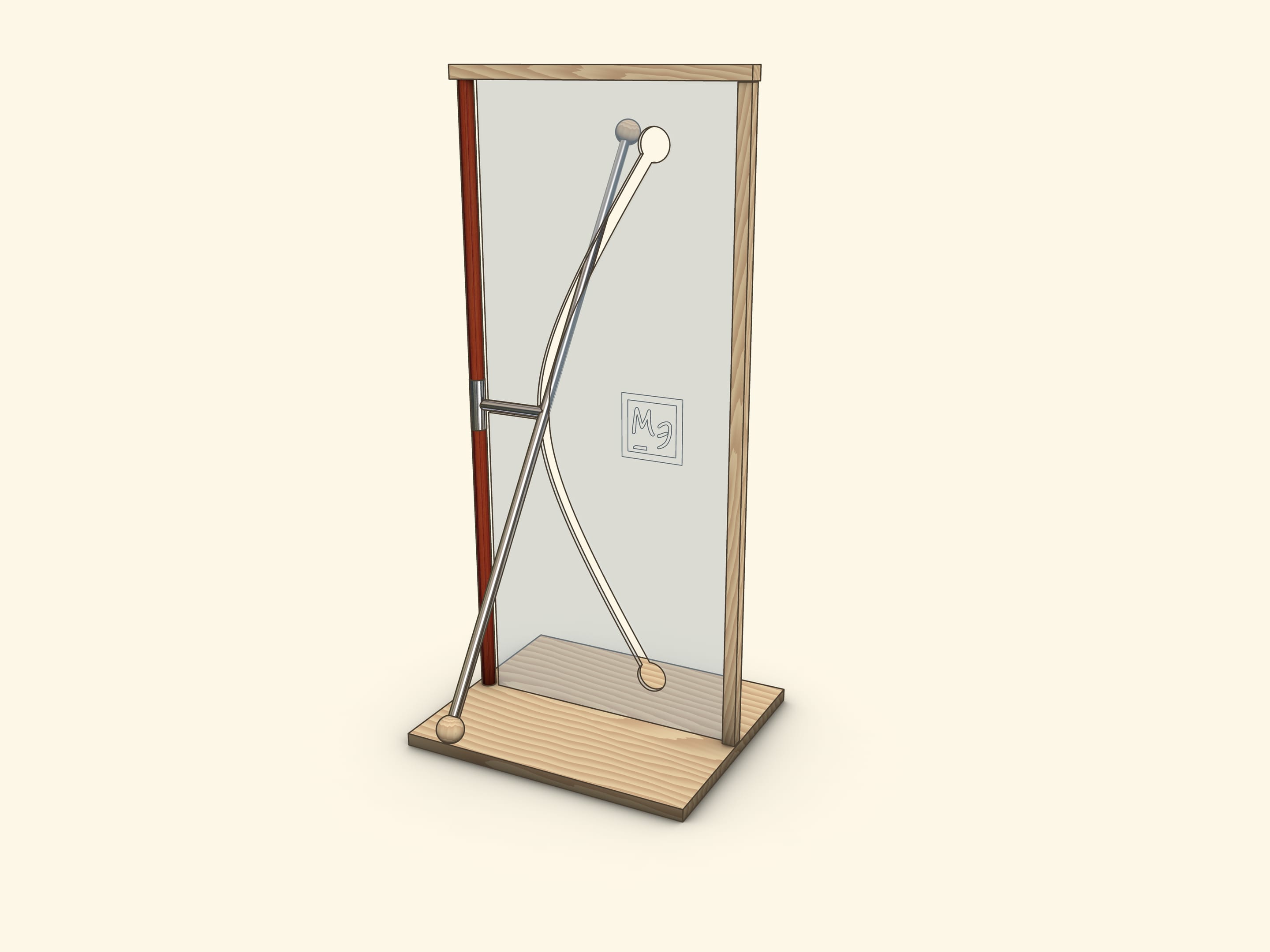
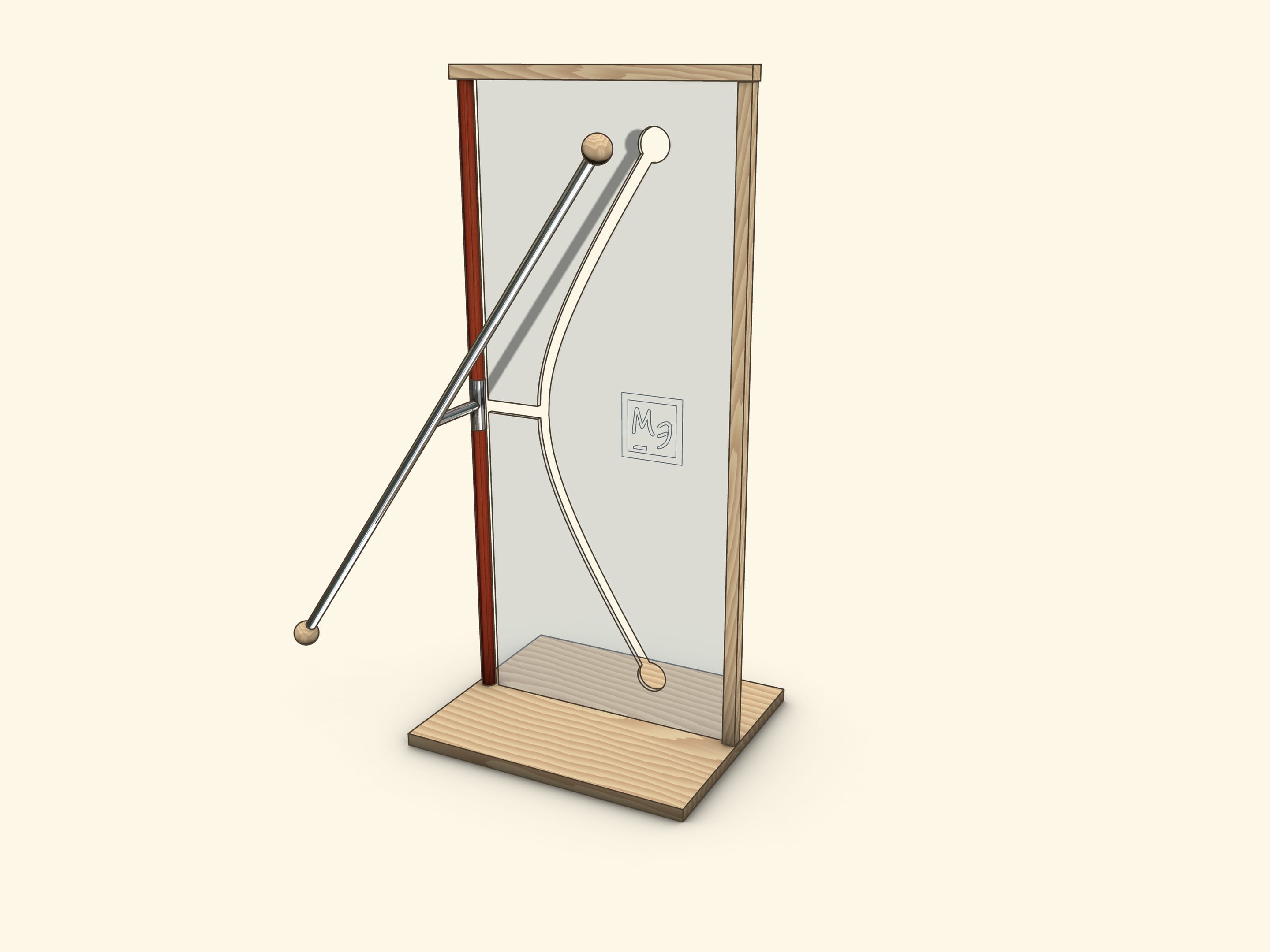
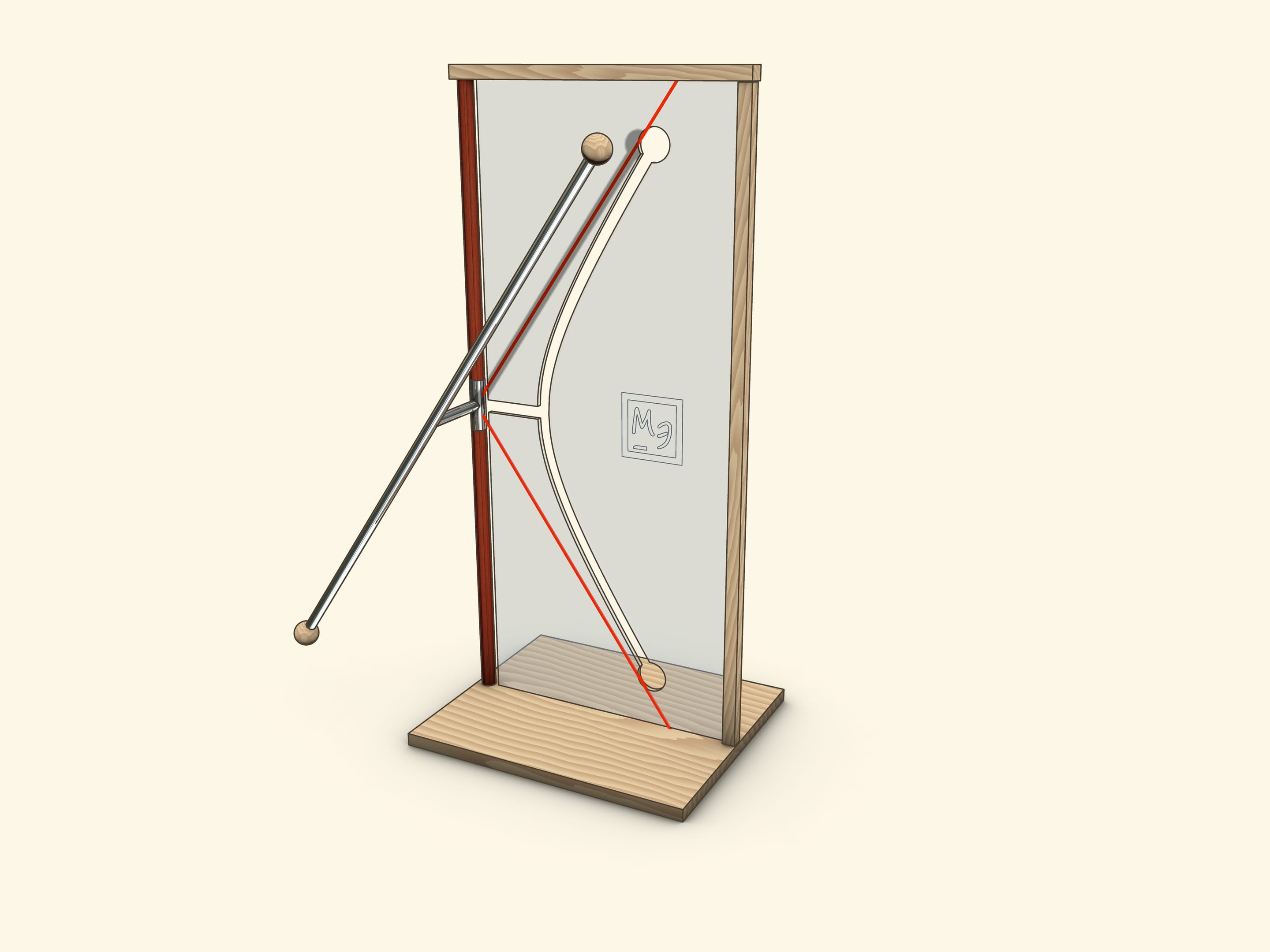
Joining these views on a hyperboloid of rotation is a base of spectacular and illustrative models, where a straight rod passes through a curved hole — hyperbola.
A showpiece, where a reclinate segment, being a part of a hyperboloid generatrix, is settled on a rotating disc, is the most interesting. During the rotation of the disc a segment passes through both branches of a hyperbola, not touching edges.
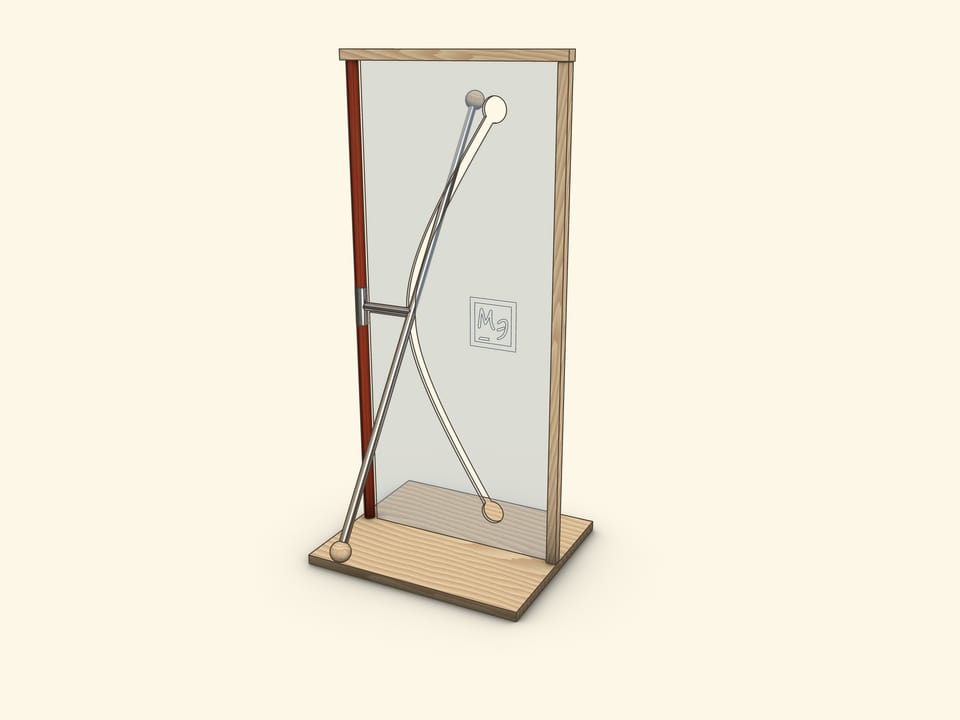
In a showpiece, which we often meet in science museums, a tube, which represents a straight line, crossing a rotation axis, is firmly connected by segment with a socket on a rotation axis.
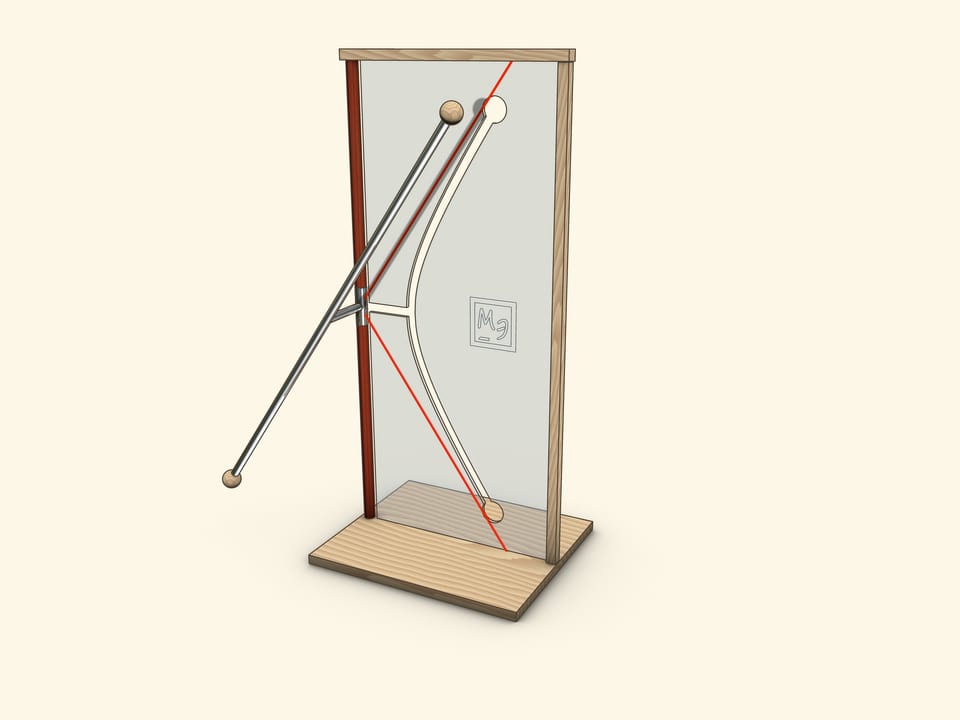
Parameters $a$ and $b$ of hole-hyperbola, intended by an equation $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ in a screen plane (in case of a naturally implemented coordinate system) can be easily counted by two typical positions of a model.
When a segment, which forms a generatrix and an axis, lies in the plane of the screen, its end coincides with a “vertex” of a hyperbola. It means that a parameter is simply length of this segment.
When a generatrix is parallel to the screen, its projection on the screen is an asymptote for a hyperbola-slash. Consequently, a parameter can be defined from the relation $\tg \alpha = \frac{a}{b}$, where $\alpha$ is an angle of generatrix to a vertical axis.
Other models in “Conic sections: hyperbola”
