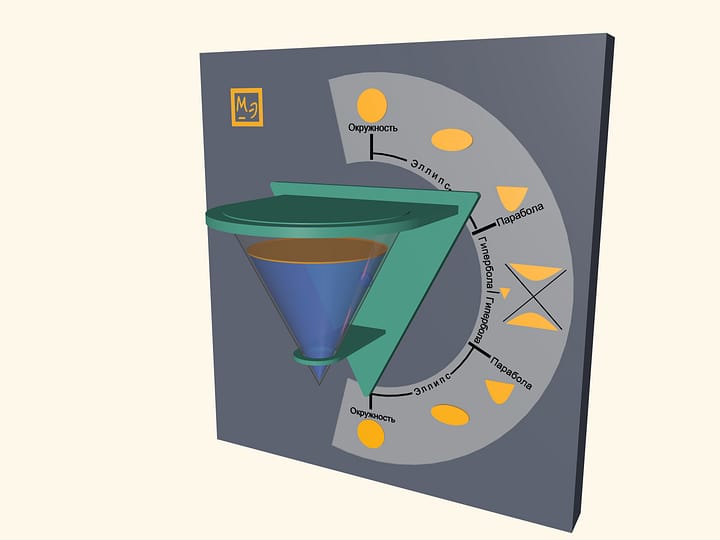
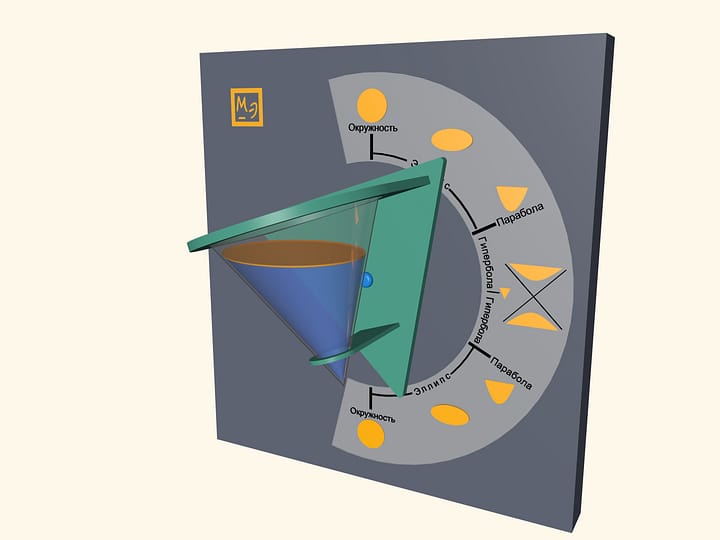
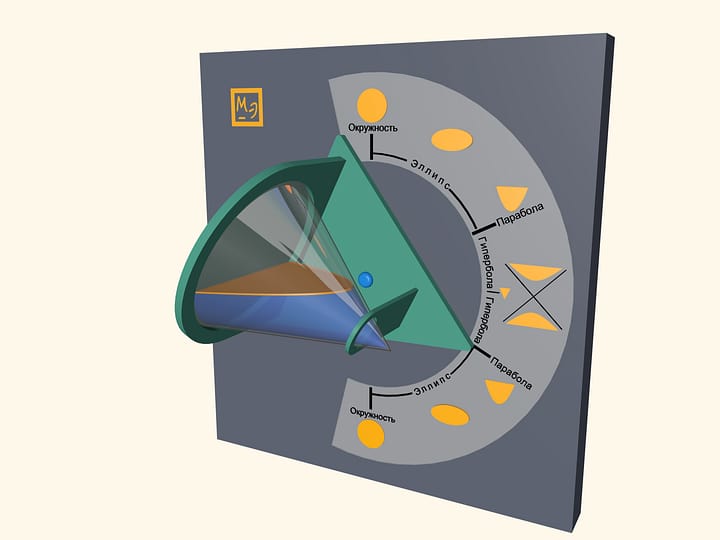
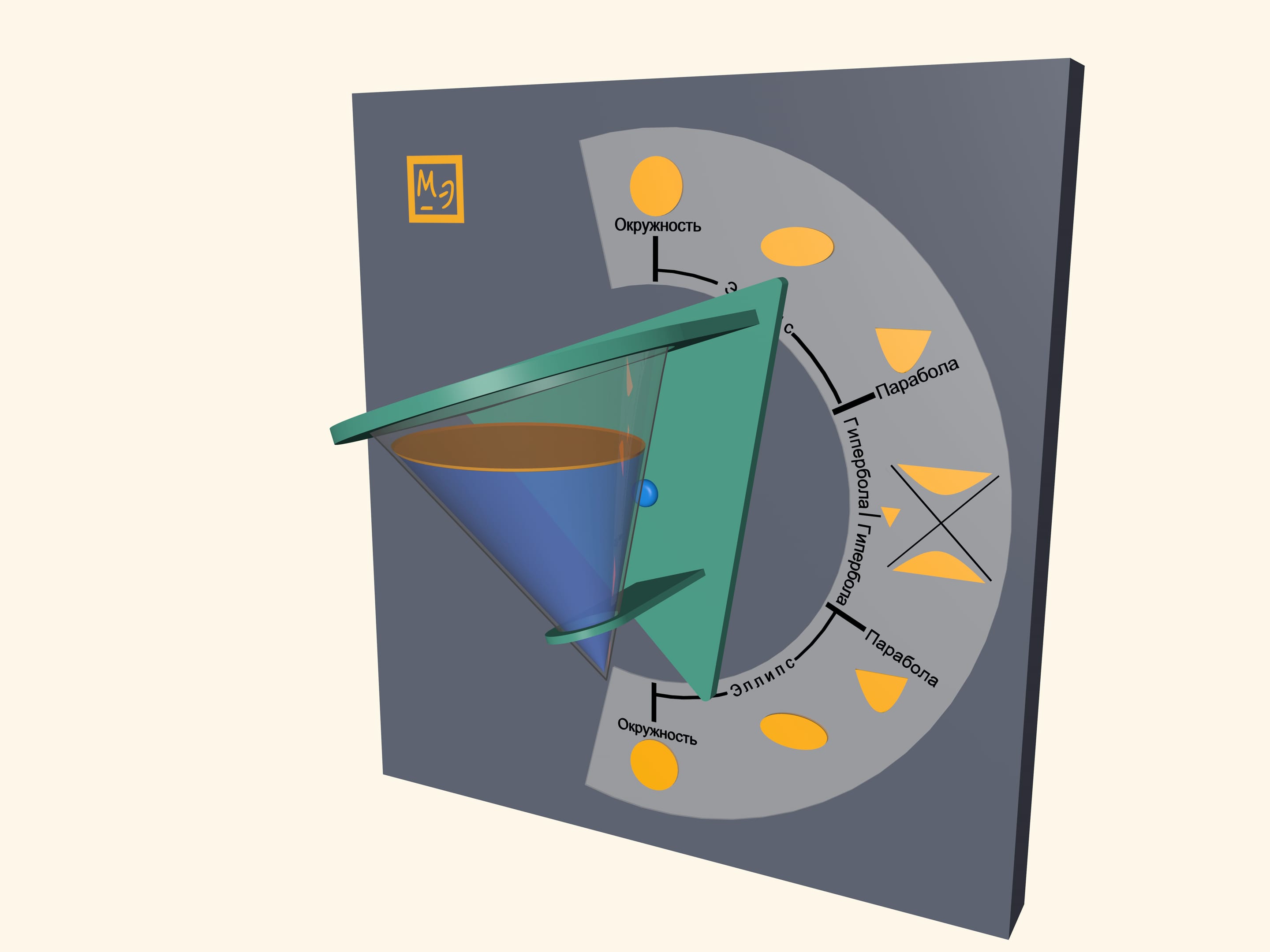
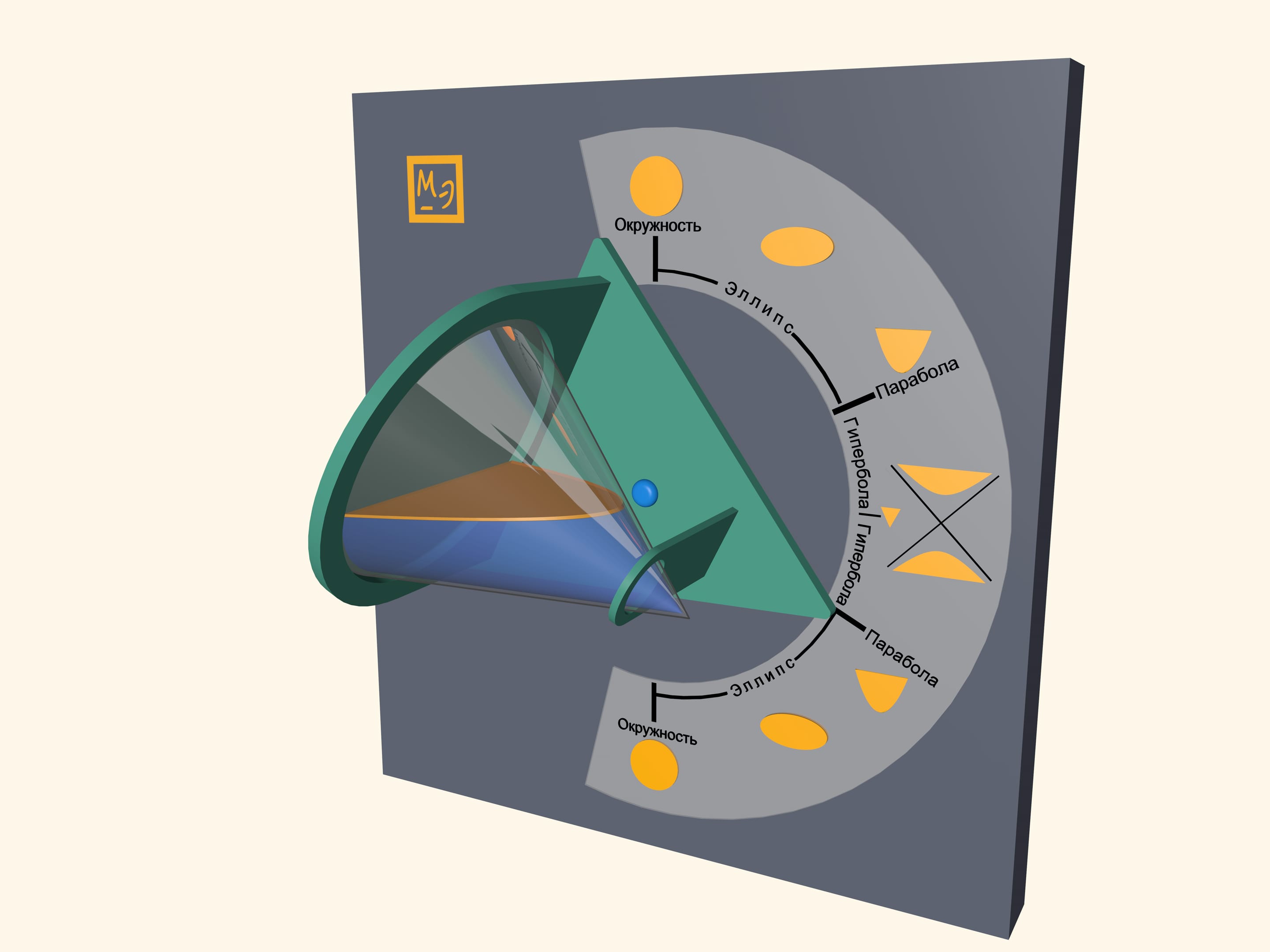
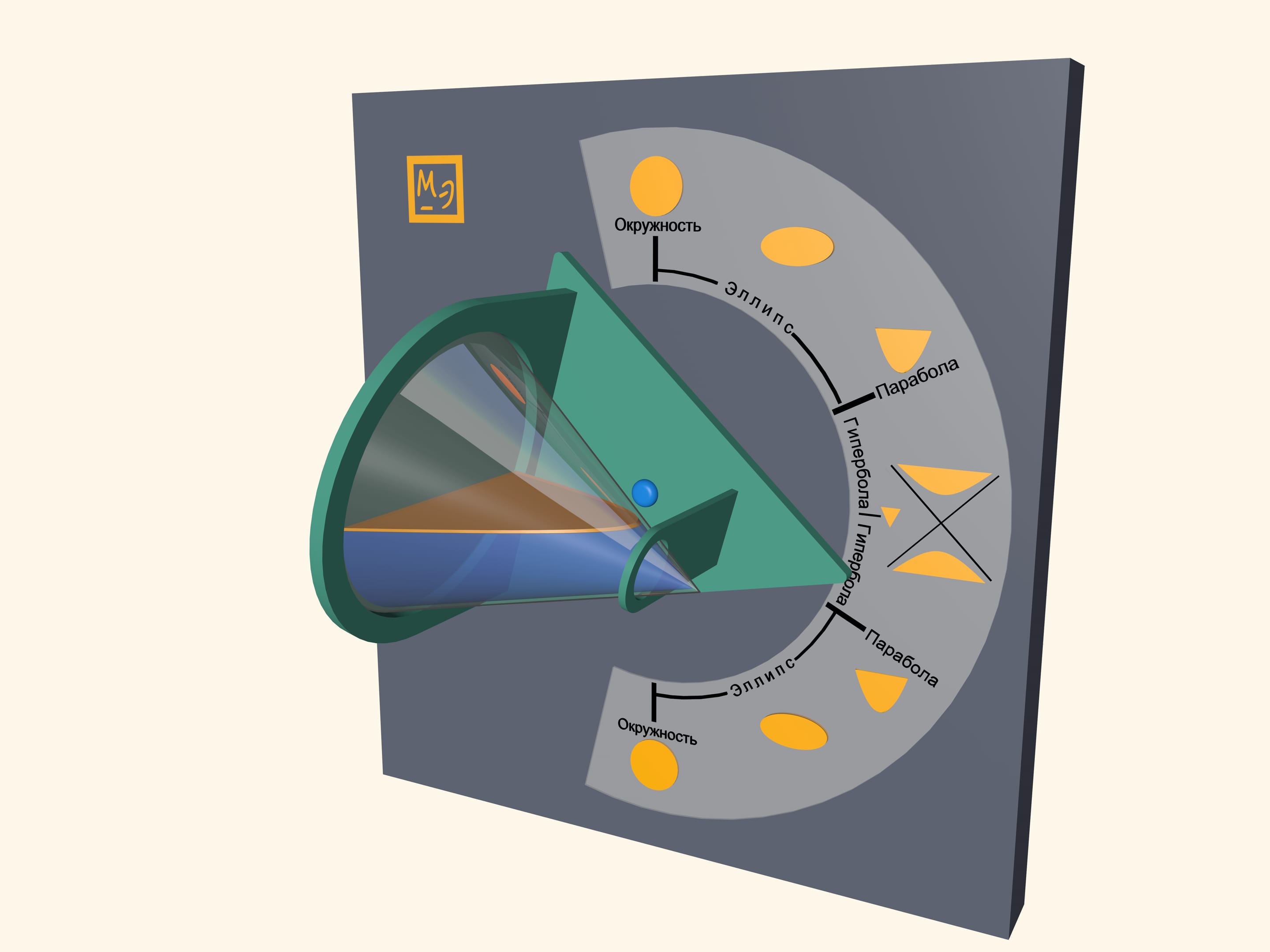
Pour some water in a transparent cone and close it with a lid, which is a base of a cone. Water surface will take a shape of an ellipse, a parabola and a hyperbola– at different angles of cone. One can also observe some degenerate cases. In a vertical position of a cone water surface will be a circle–it is a limiting case of the ellipse. In a horizontal position of a cone water surface will be a triangle– a hyperbola degenerates into two intersecting straight lines.
Look at the first image when the cone is positioned vertically, pointing down. Which part of the cone do you think is filled with water? Then look at the last image, where the cone is positioned vertically, but pointing up. It appears that the almost full cone has become almost empty. However the water volume hasn’t changed, has it? This effect is related to the volume distribution in a cone. In fact, the volume of poured water is half the cone volume. You can see that by looking at the horizontal position of the cone.