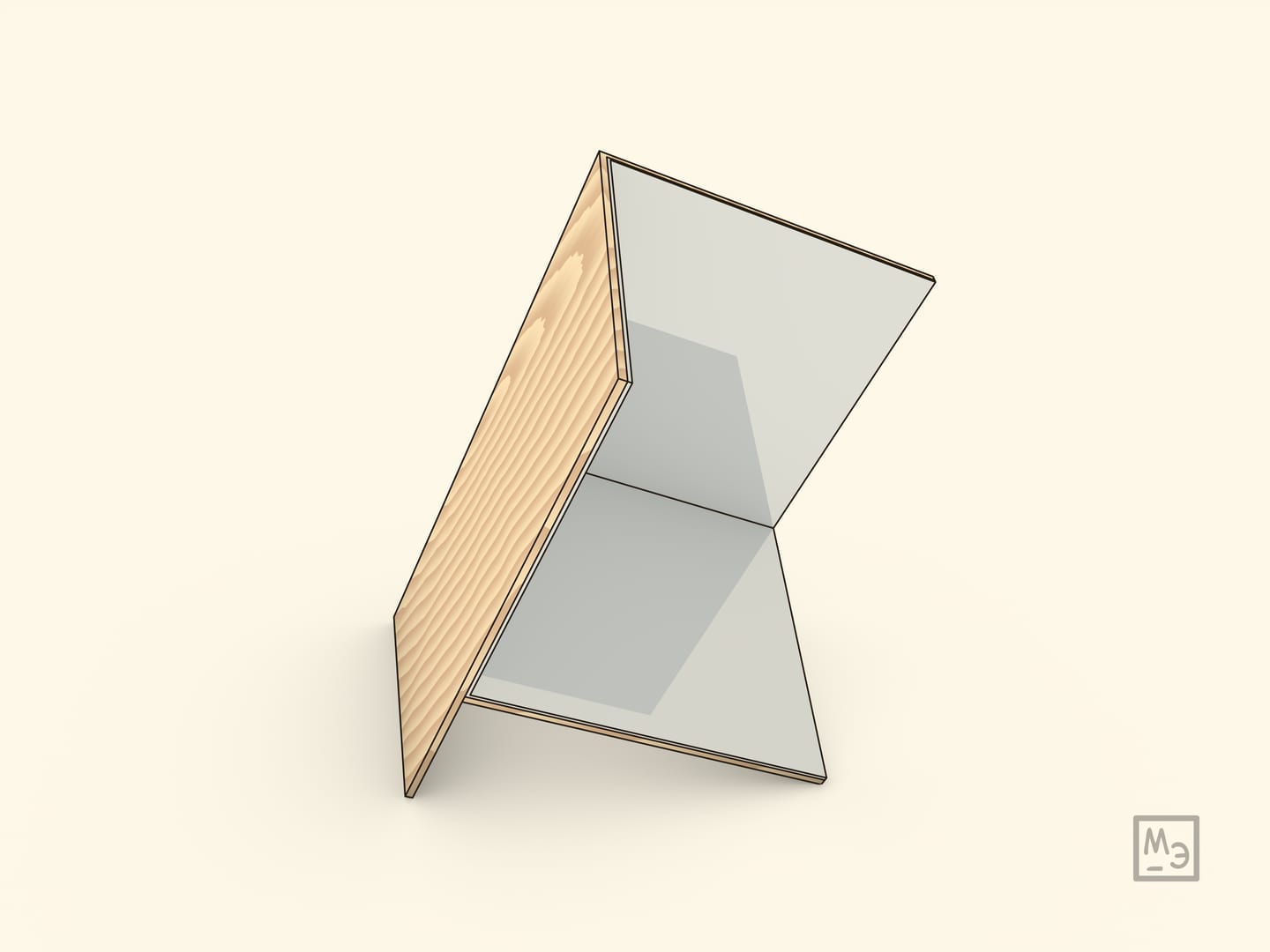
Corner reflector is amazing in its “incomprehensible efficiency”: the simplest device — three mutually perpendicular reflecting planes — has a whole range of applications on Earth and in space, too! A reflector on a bicycle or car consists of a large number of these small corners, and large corner reflectors — for radio waves — are installed on water buoys and small yachts. And the reflectors on the Soviet Lunokhod-1 and Lunokhod-2 moonlanders, as well as those on the US Apollo programme, are being used in an ongoing experiment in laser lunar location experiment — allowing measurement of the ever-changing distance from the Earth to the Moon with great accuracy.
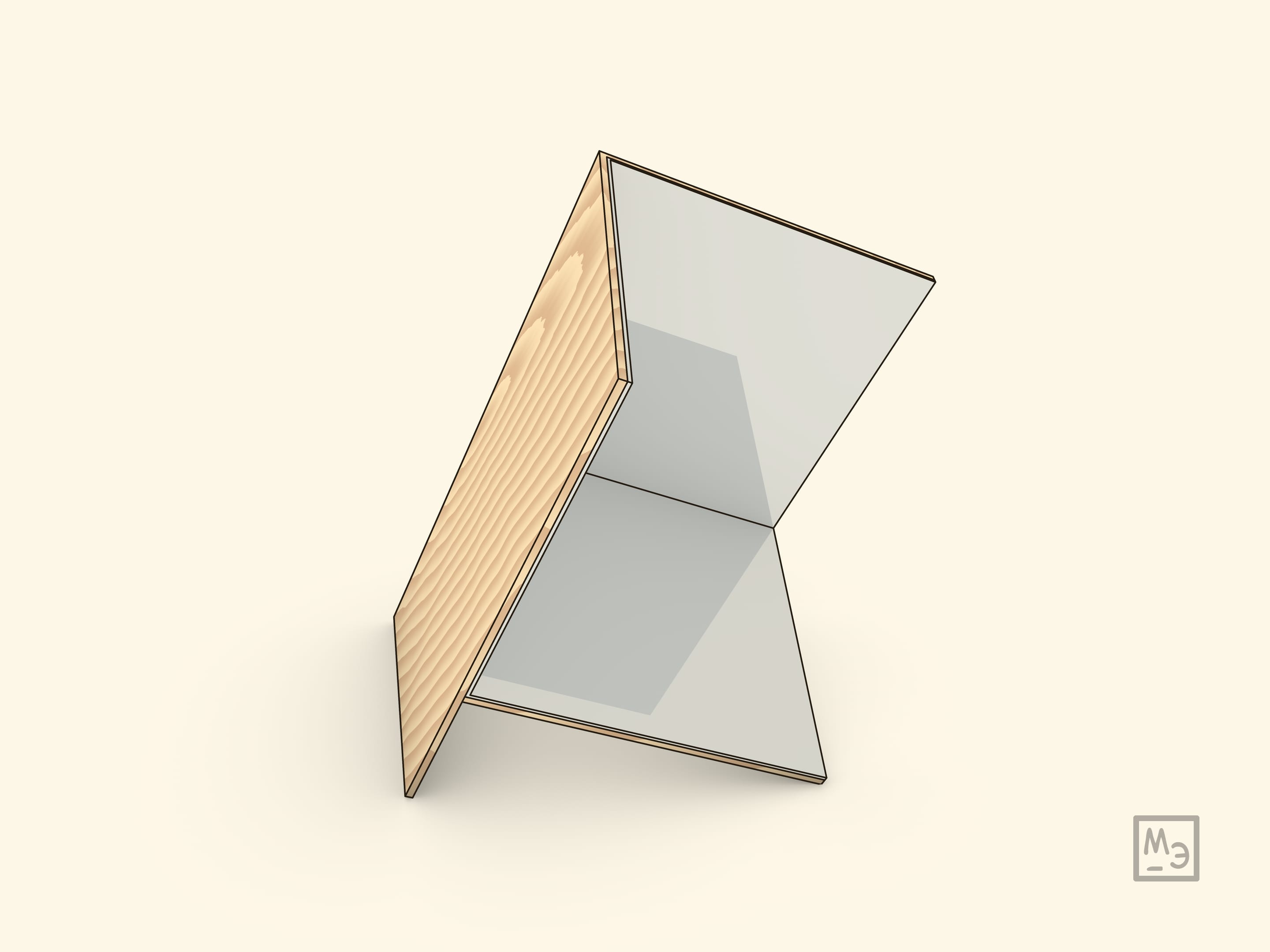
The idea behind corner reflector is simple: a beam (of light, ...) reflecting off three mutually perpendicular mirrors goes “back” — parallel to the direction from which it came. If the direction of the initial beam is given by vector with coordinates $(a; b; c)$, then after reflection of the beam from the plane $xOy$ its directional vector will be $(a; b; -c),$ and after consecutive reflections from planes $yOz$ and $zOy$ — $(-a; b; -c)$ and $(-a; -b; -c)$ respectively.
Unlike headlights, a reflector (consisting of a large number of small corner reflectors) requires no energy and contains no bulbs. But if it is attached to a bicycle, motorbike, car, if you turn even a small part of a pedestrian’s jacket or a road sign surface into a reflector with a special coating, the driver of the car, whose headlights have illuminated one of the above-mentioned objects, will immediately see it because of the light reflection from the reflector.
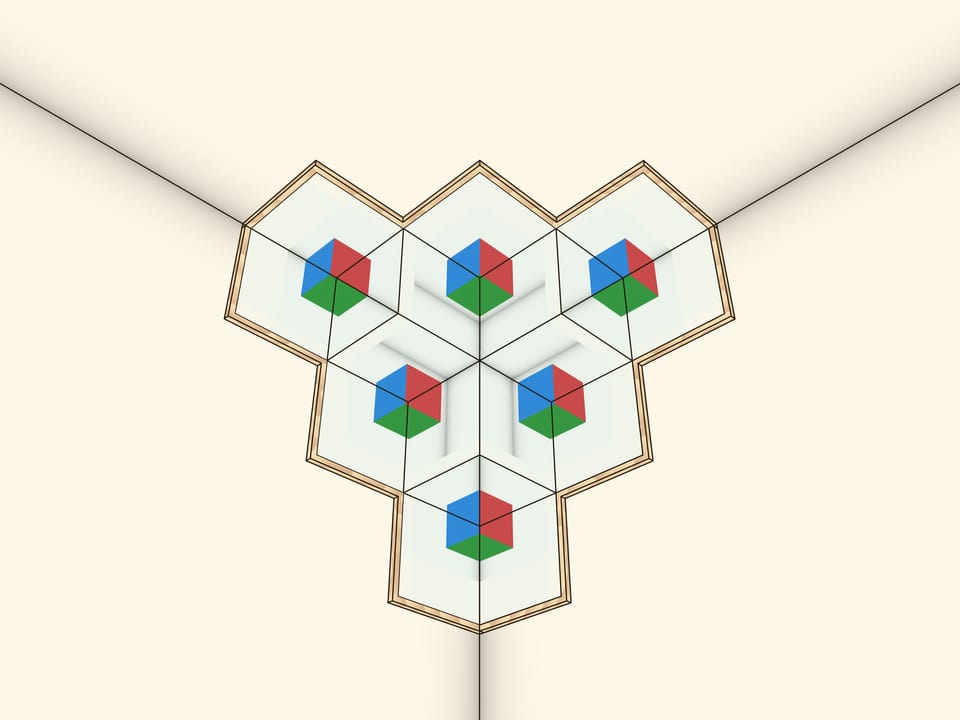
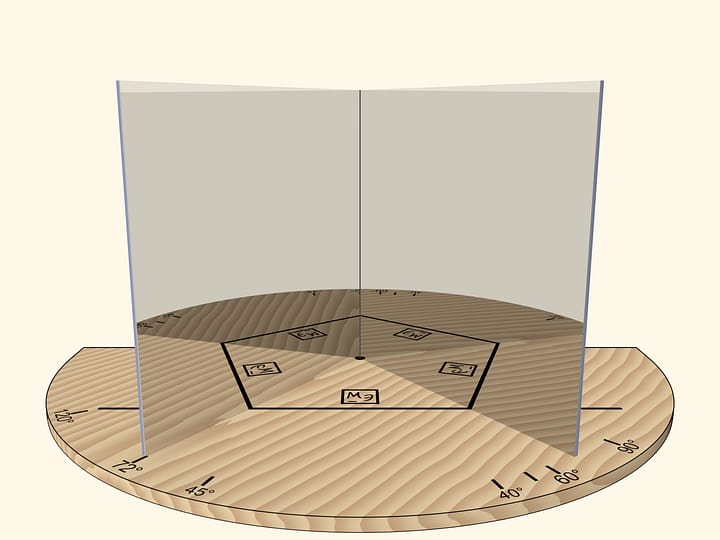
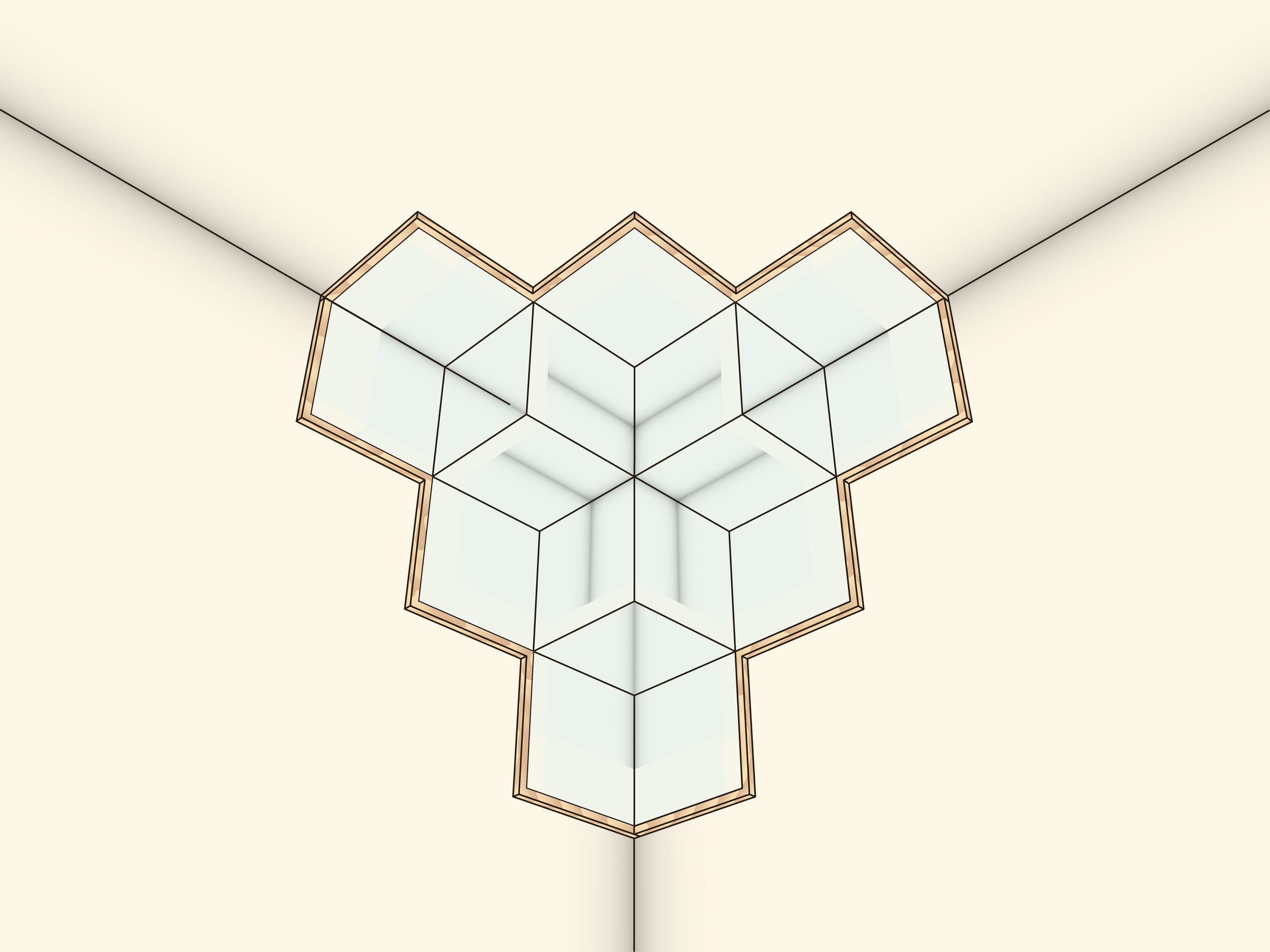
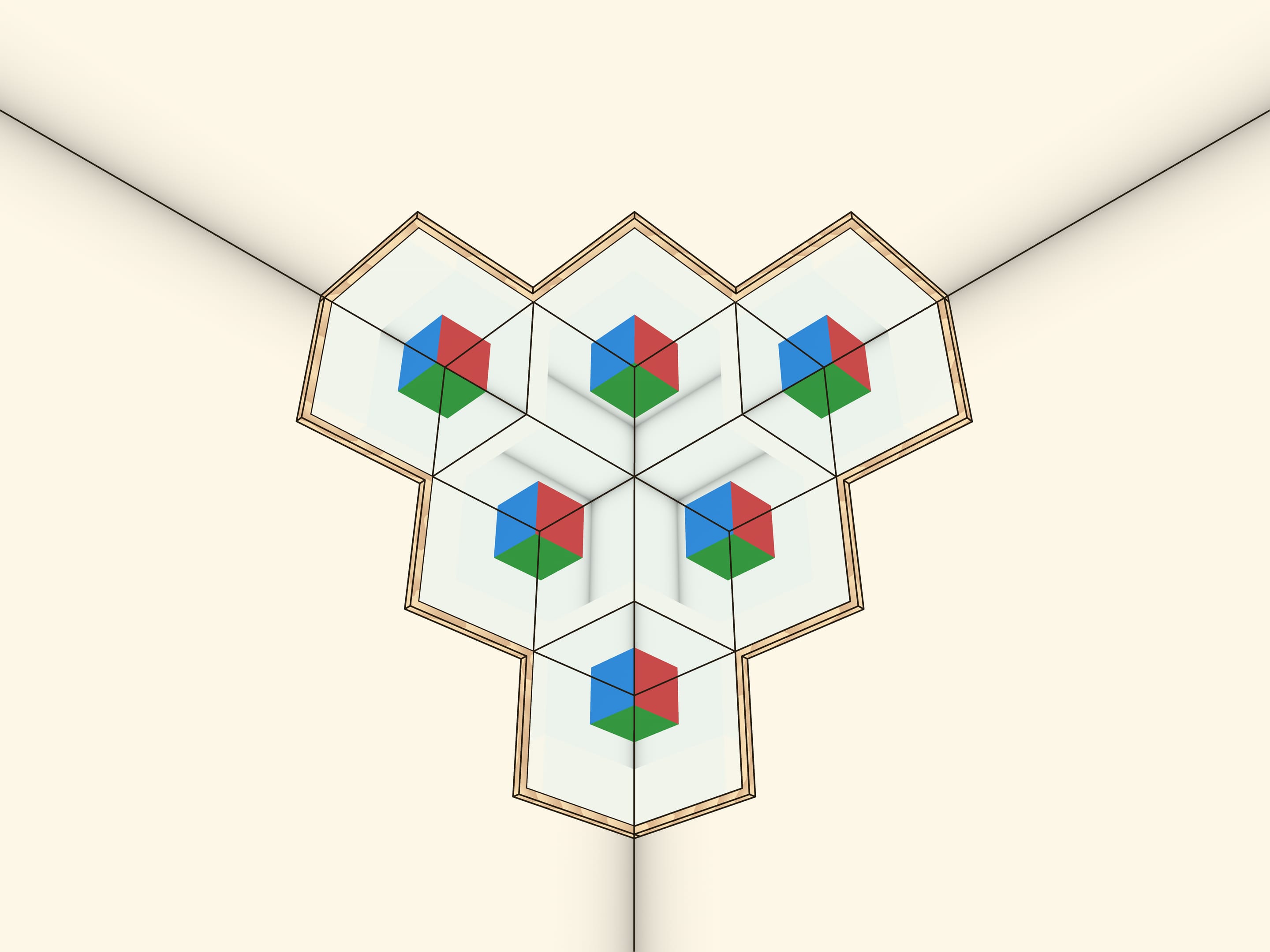
Large corner reflector is easy to make by cutting mirrors at your local workshop. It’s also possible to make it yourself out of plastic — there are plastics available now that have a good reflection coefficient. Once you make a big model you can see that reflection in the corner reflector follows you when you move. And if you stand in front of the reflector and close your eyes one by one, you will find that each time the reflection of the open eye looks directly at you and always out of the intersection of the mirror planes!
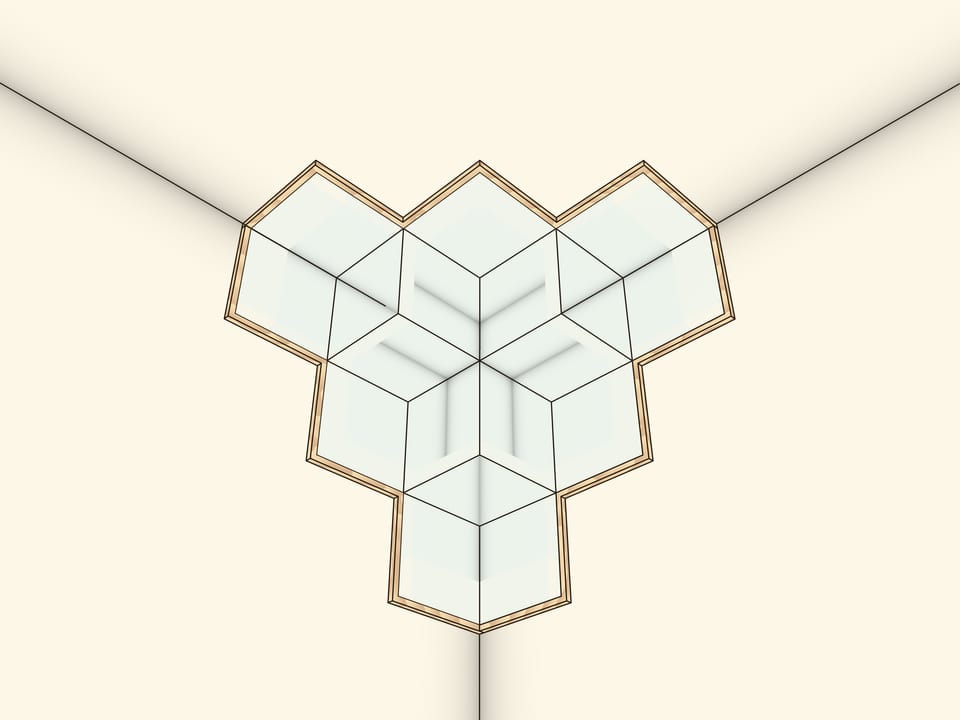
The model with a number of large corners looks spectacular when mounted under the ceiling in a school corridor.