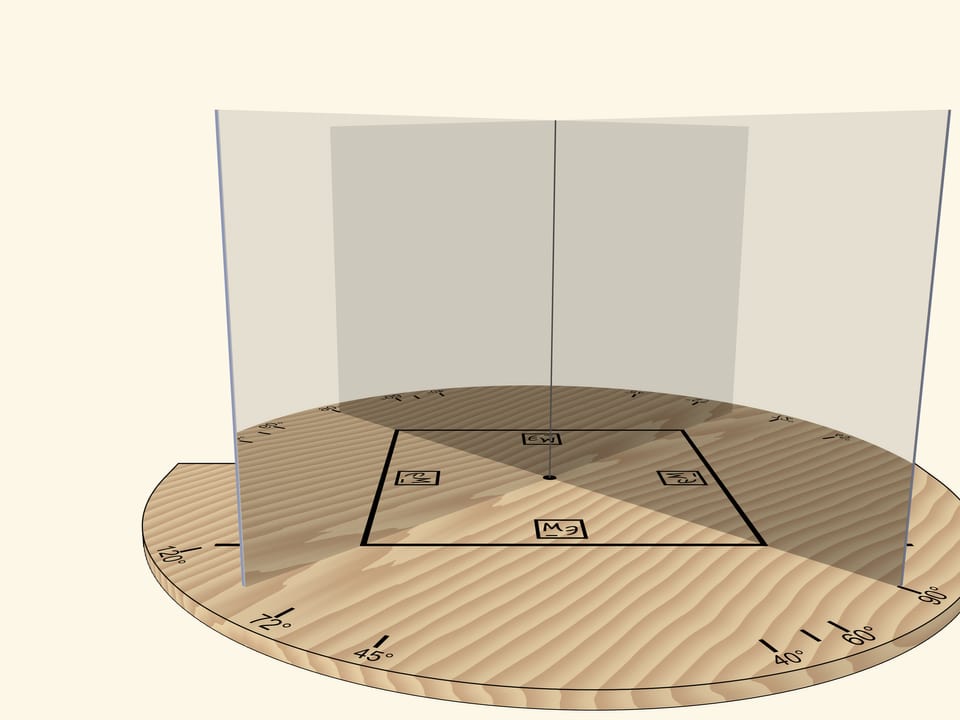
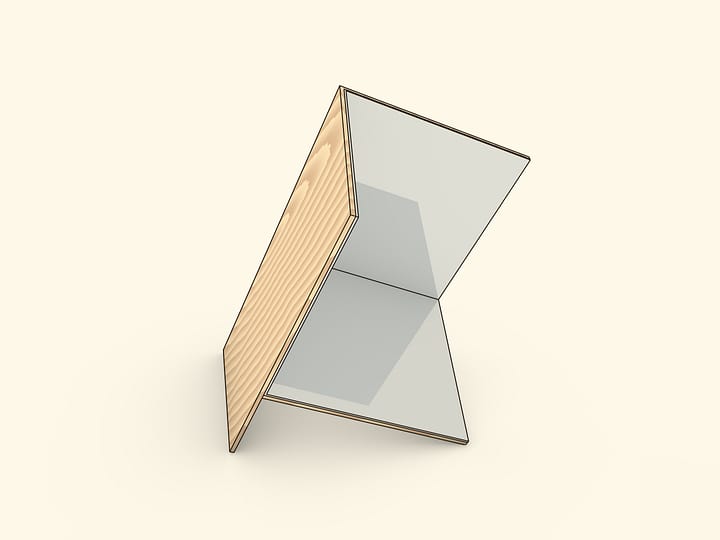
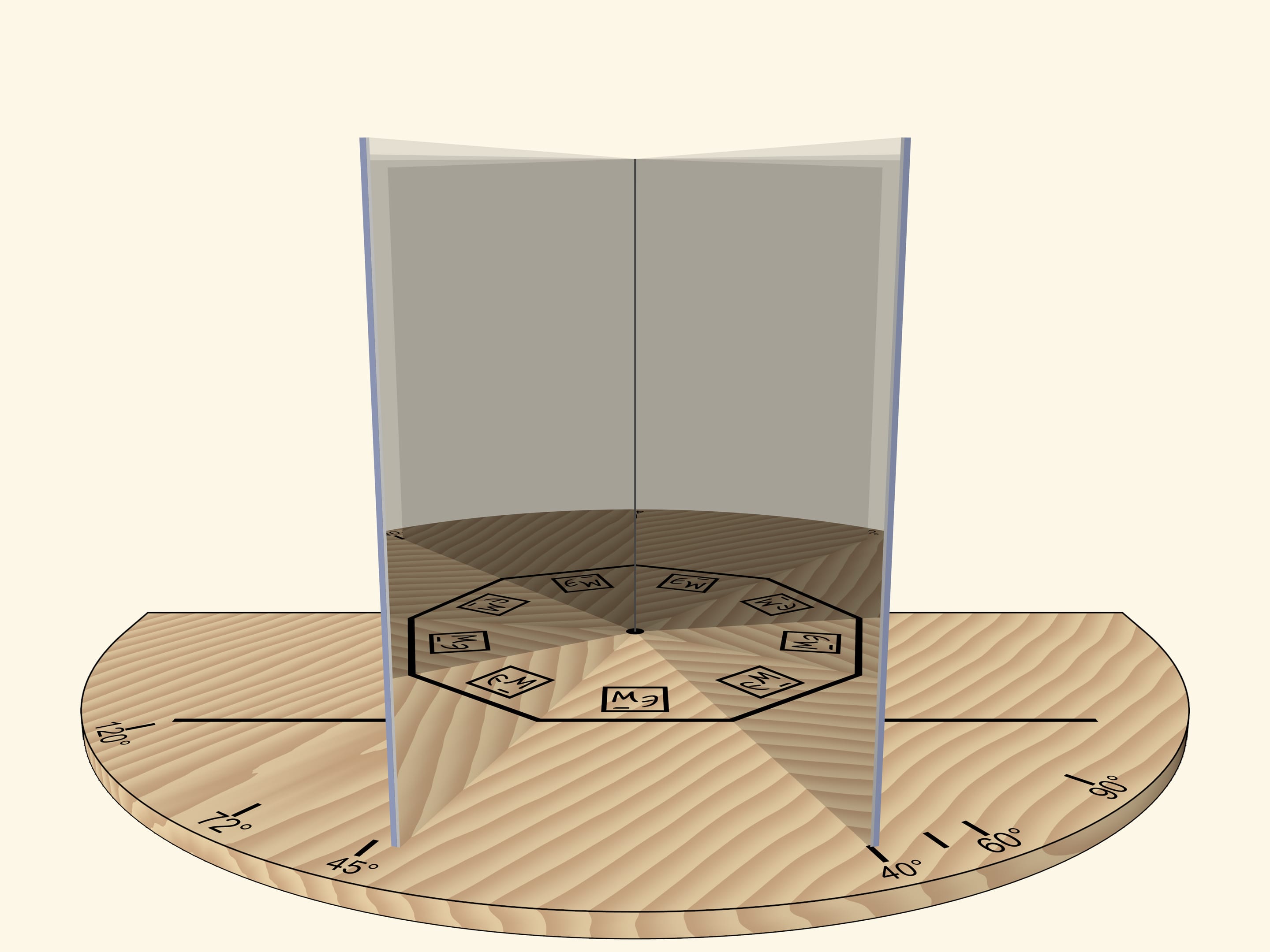
Two mirrors, placed like an open book and perpendicular to a base, help to understand how kaleidoscopes work. A segment that is reflected multiple times in this mirror book, which is a dihedral mirror angle, can turn into any regular polygon.
The dihedral group is a symmetries (self-mappings) group of a regular polygon that includes both rotational and axial symmetries. All symmetries of this kind can be produced with reflections. Let’s draw a segment on the model base and look at its reflections in mirrors. To simplify the analysis of the reflections, it’s advised to draw some asymmetric figure or put an object in the corner.
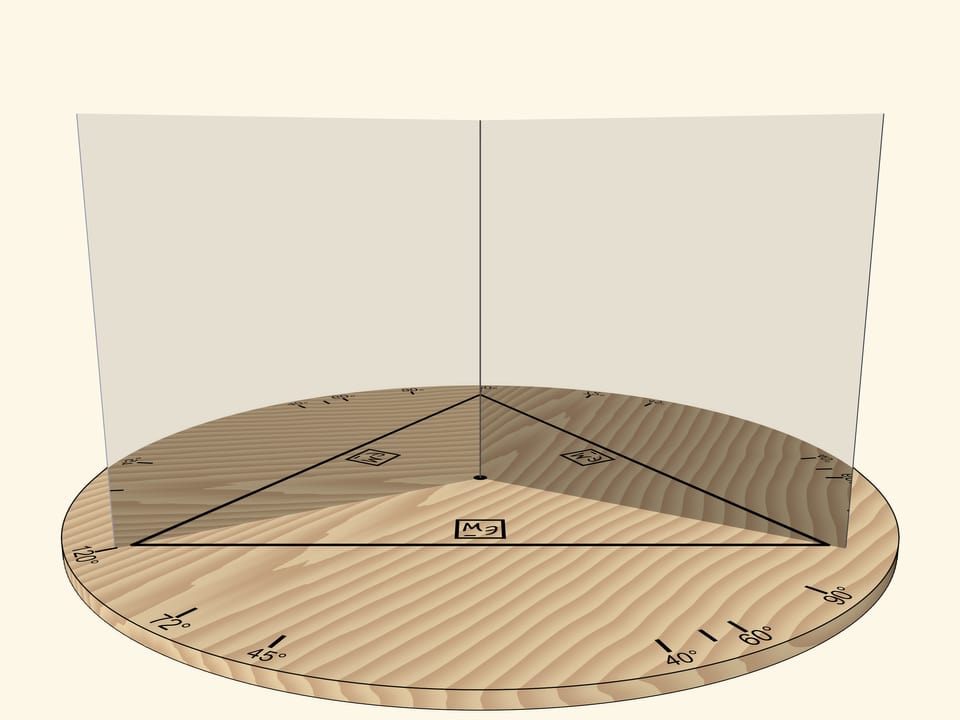
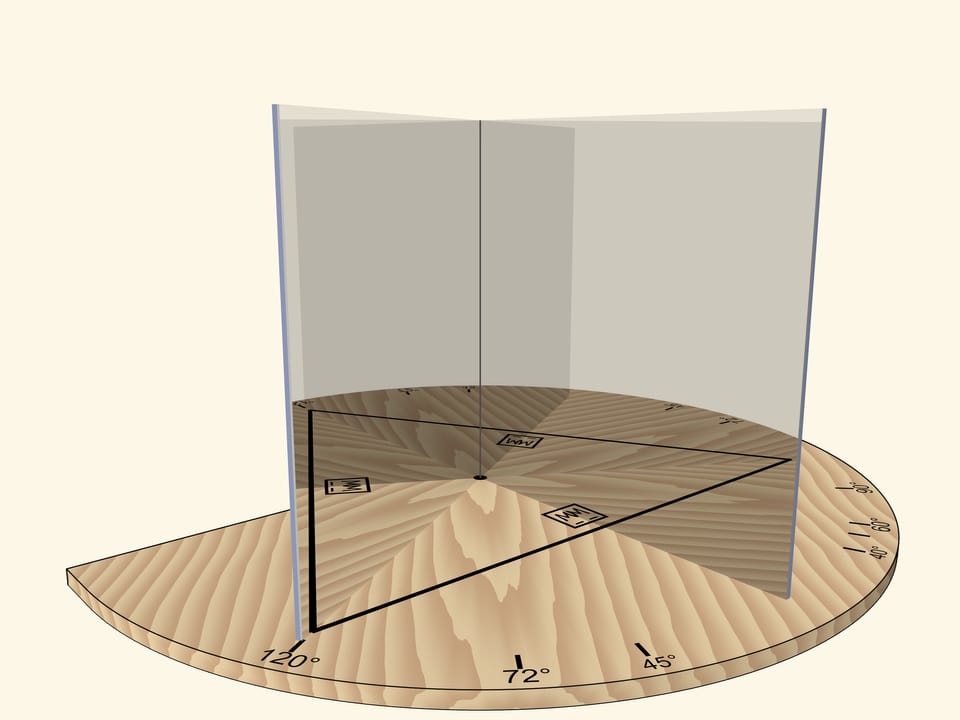
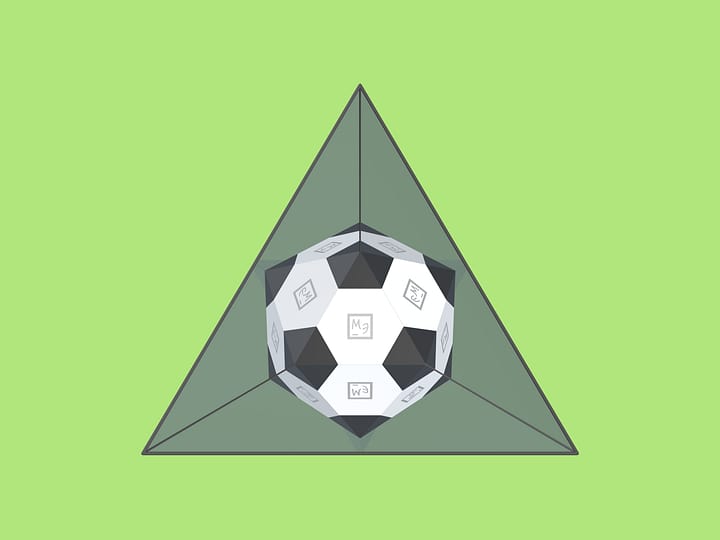
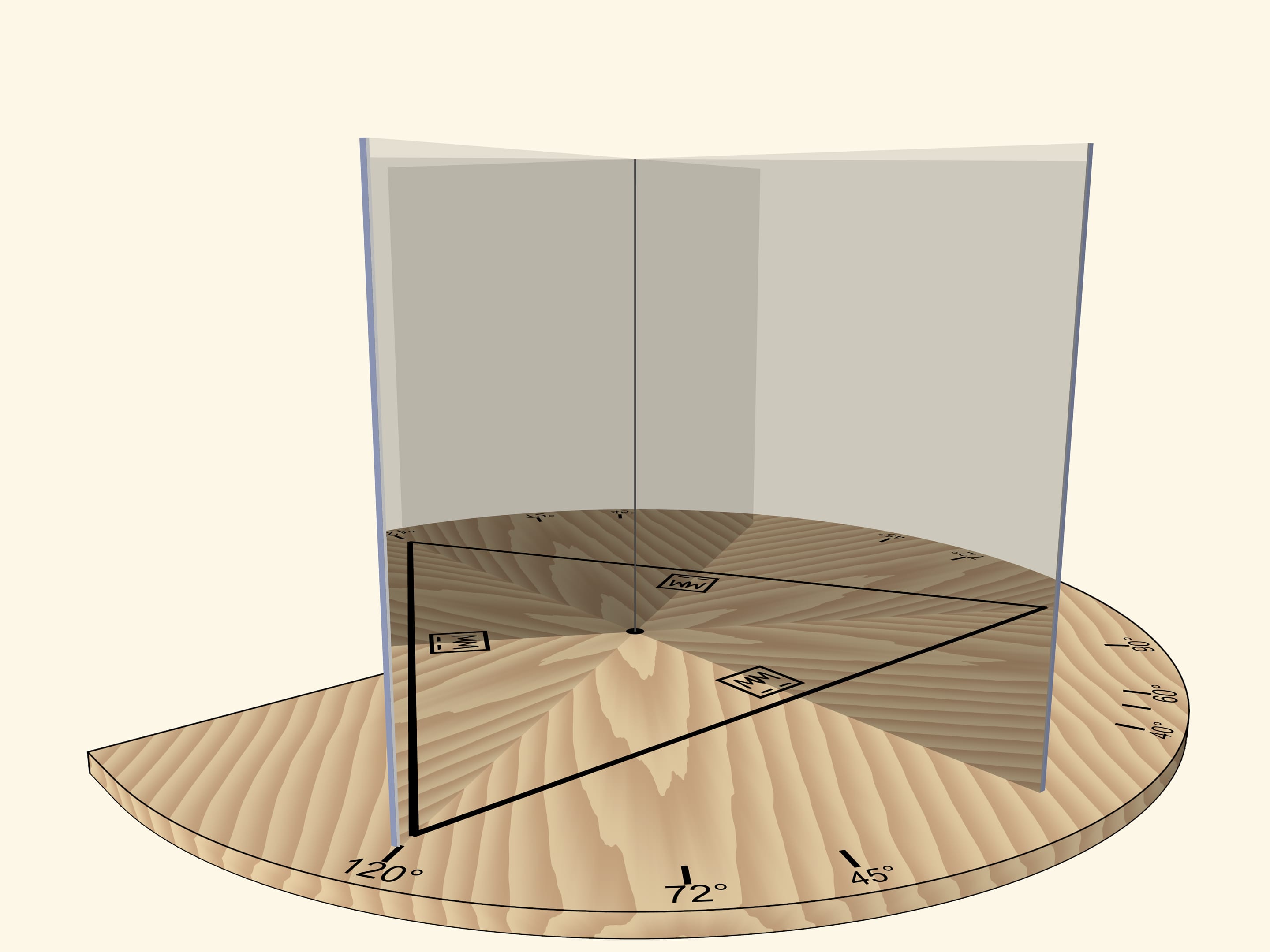
If the mirrors form an angle of $120^\circ$, the segment reflected in mirrors will produce a regular triangle.
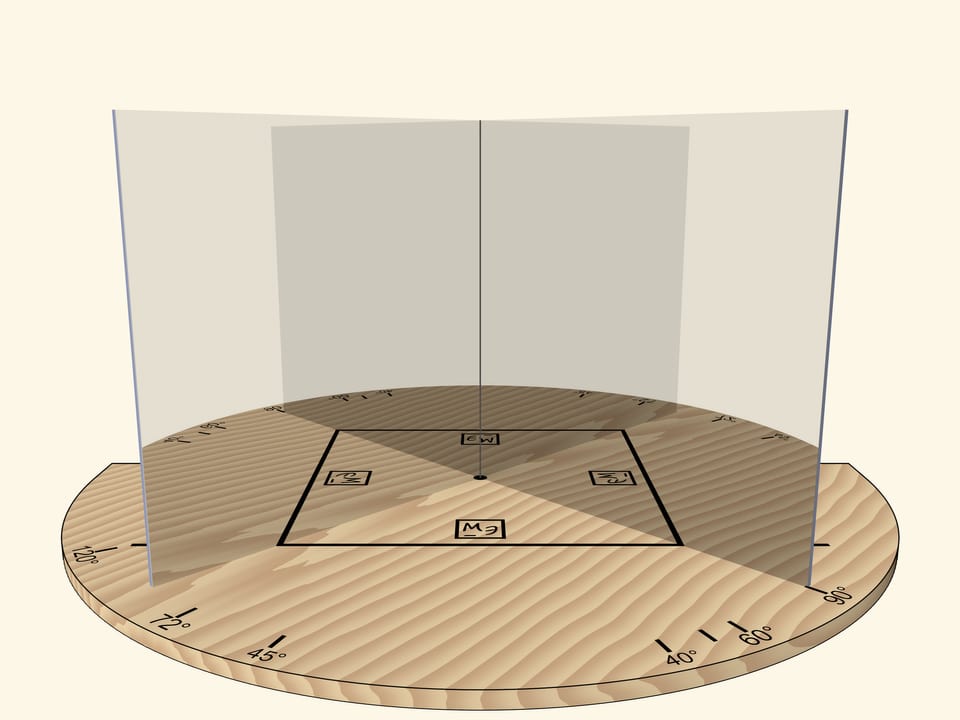
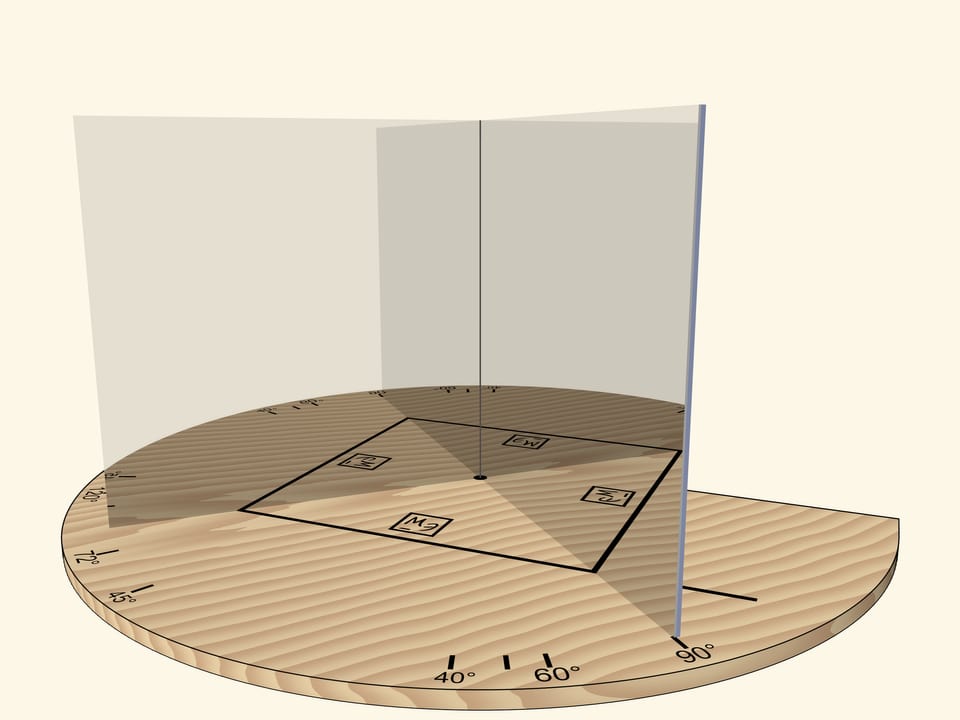
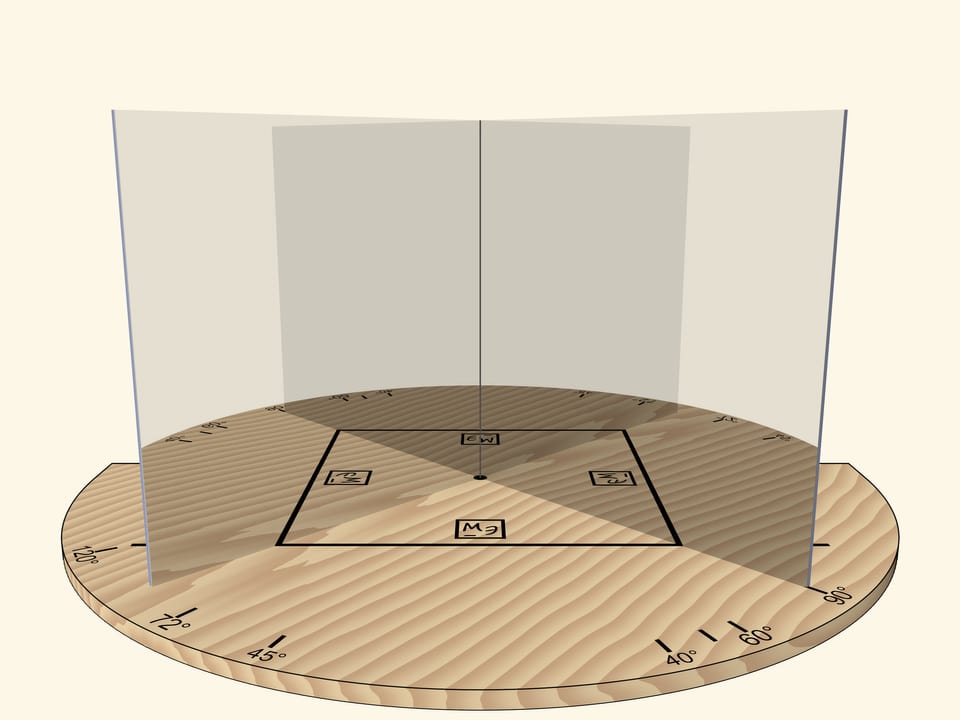
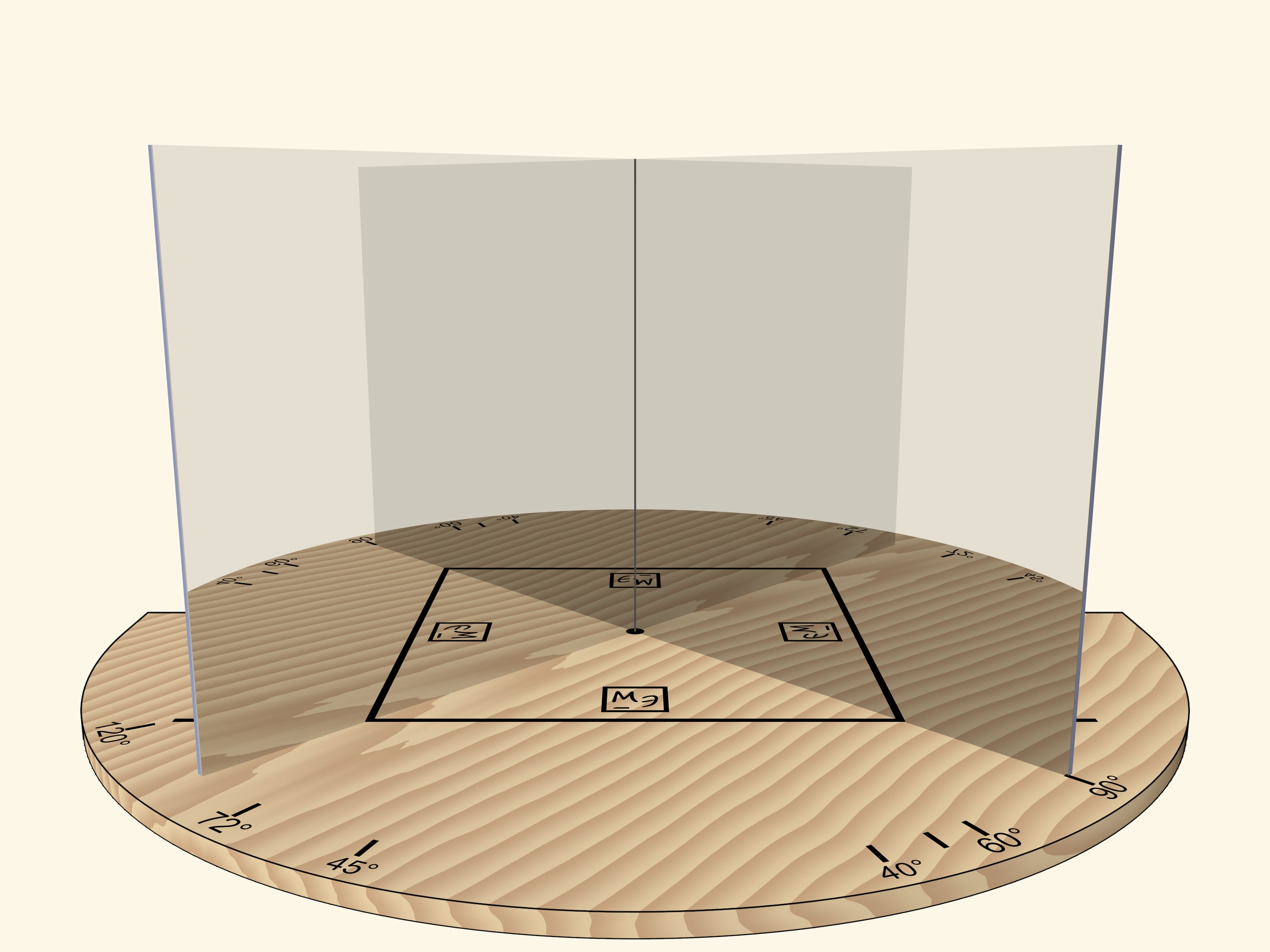
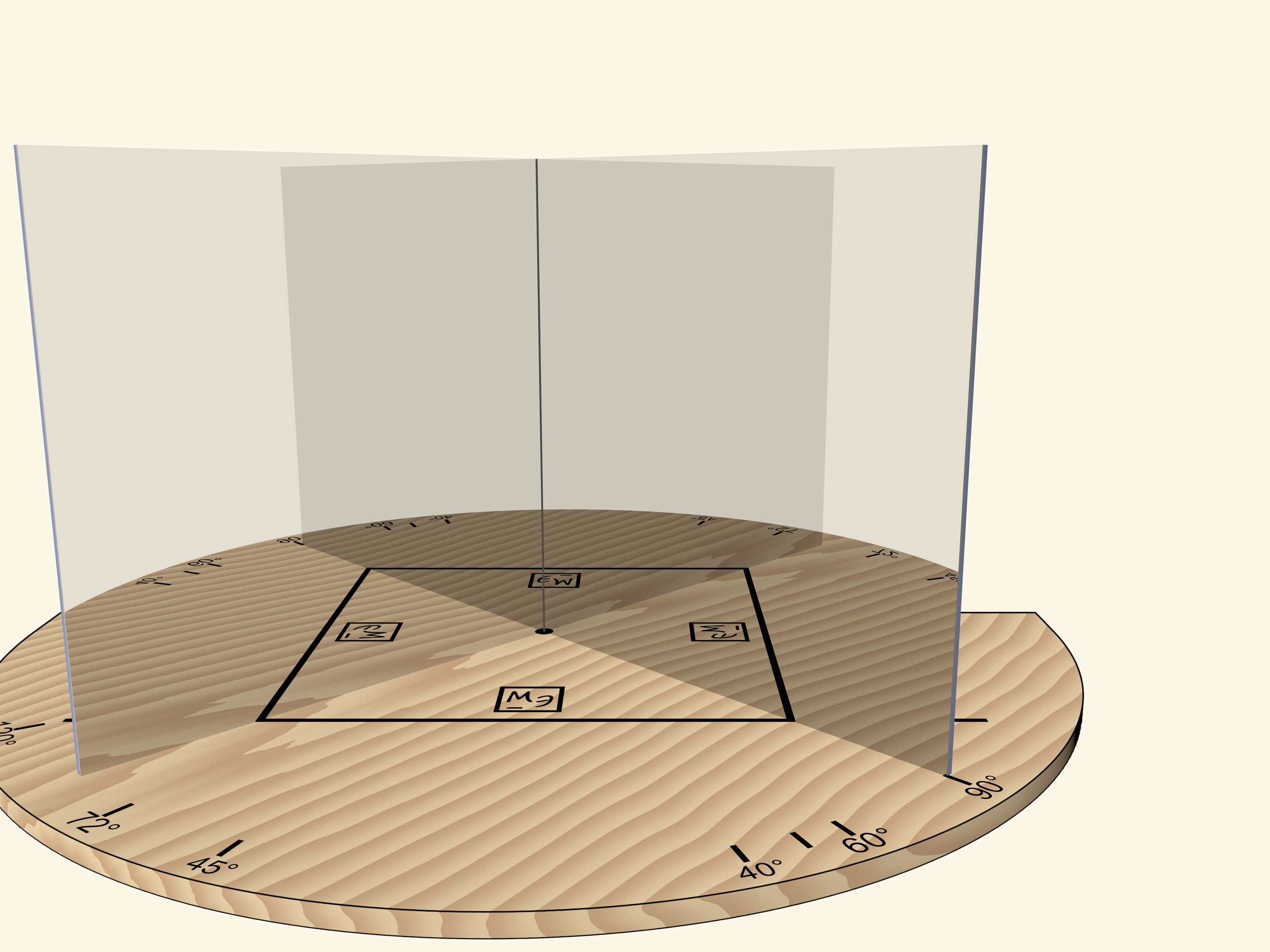
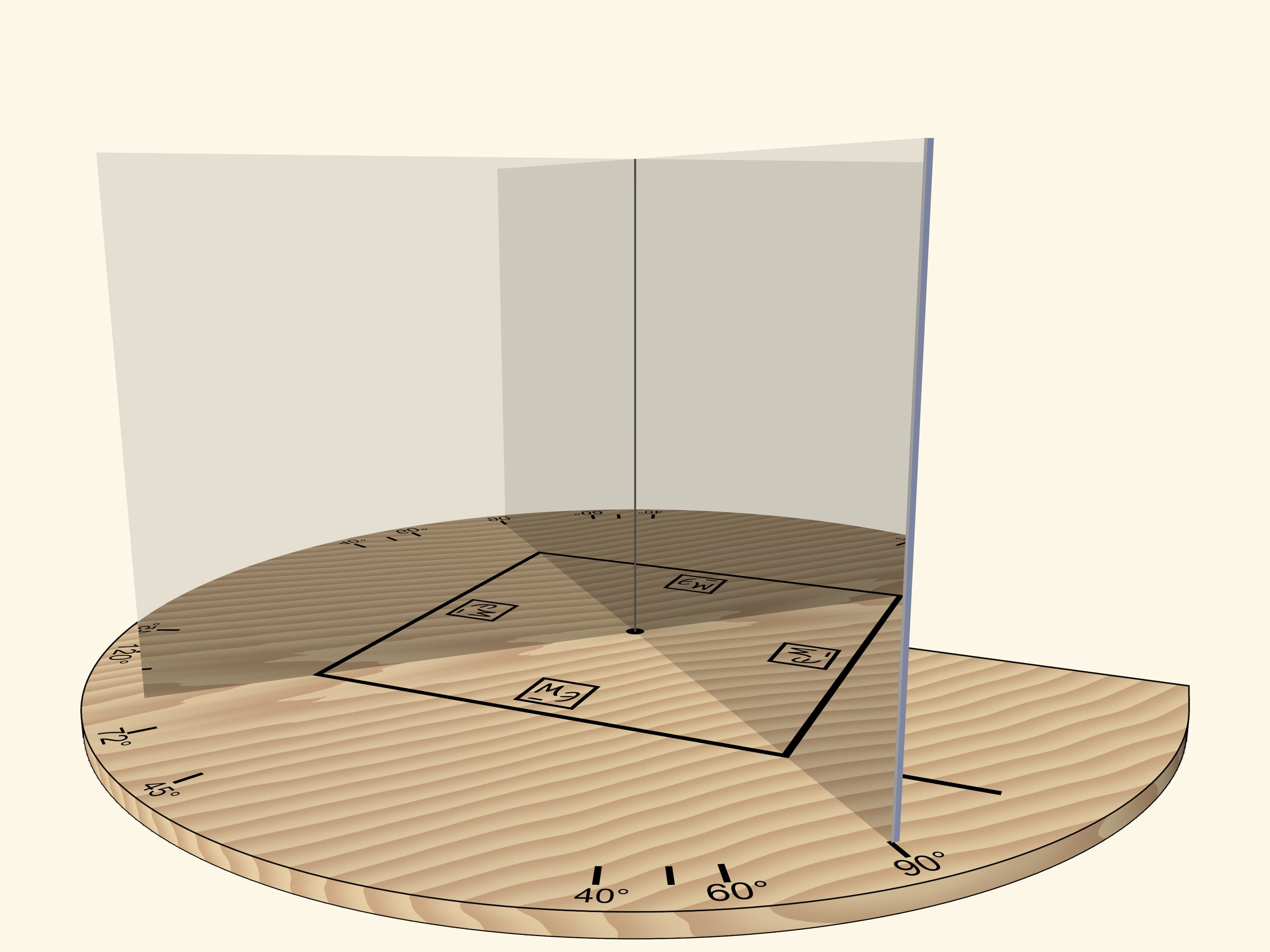
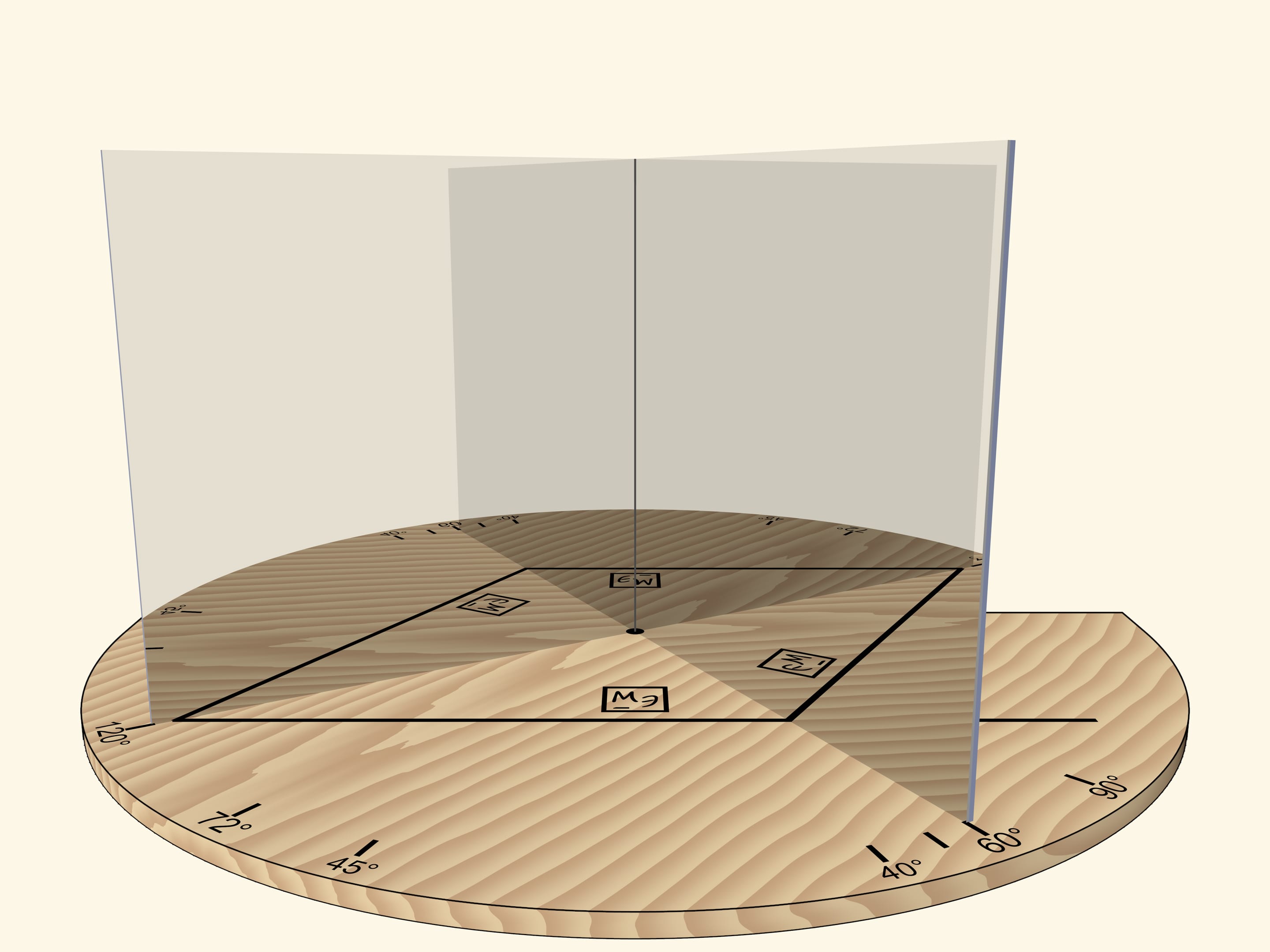
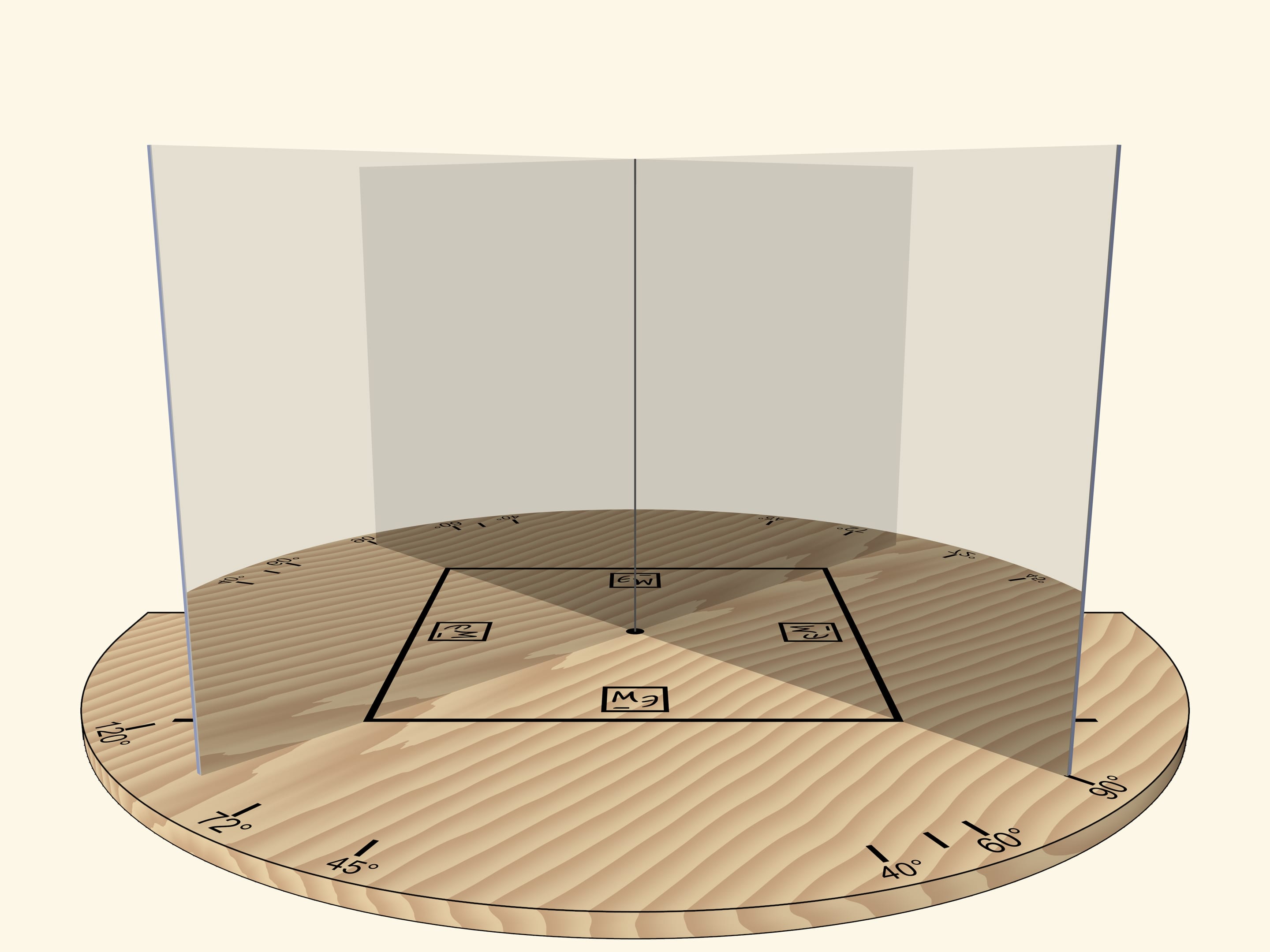
If we move the mirrors so that the angle between them is $90^\circ$, the segment will be reflected as a square. The “Mathematical Etudes” logo orientation in mirrors can be used to determine reflection level.
The main requirement to a kaleidoscope is that the image reflected in its mirrors, should be seen by the observer as a real object: if we move relative to the mirrors, the object should not change. For example, a square should always remain a square.
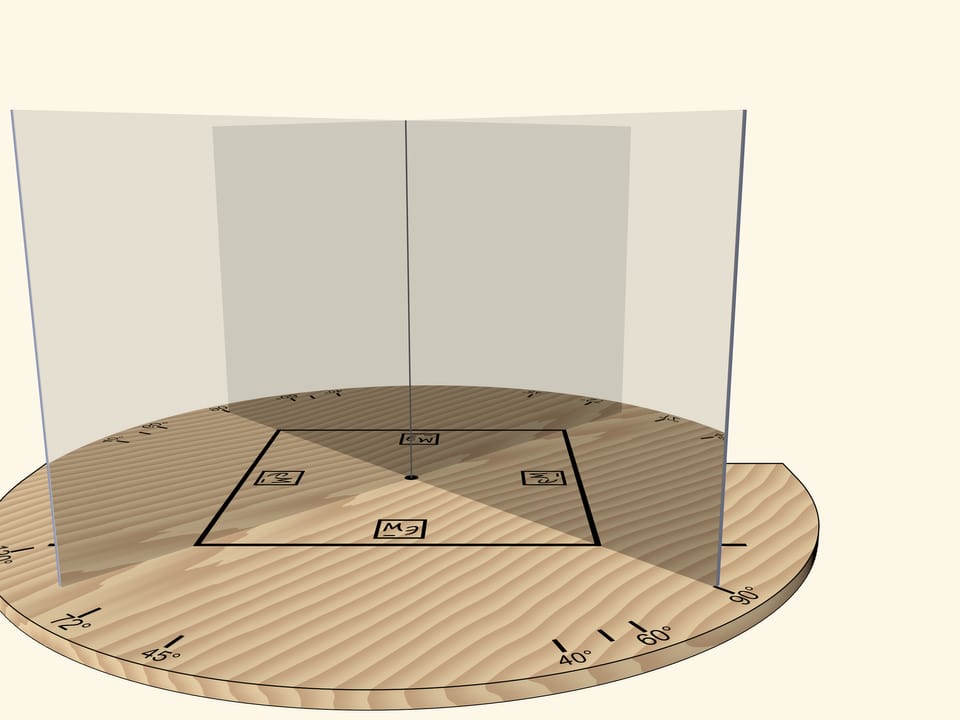
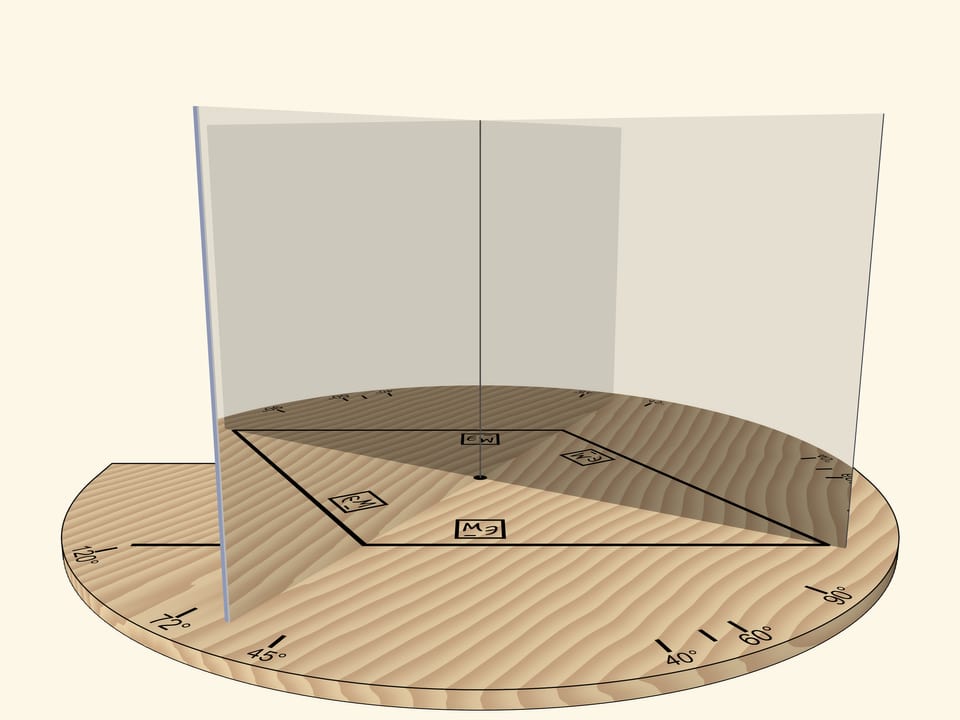
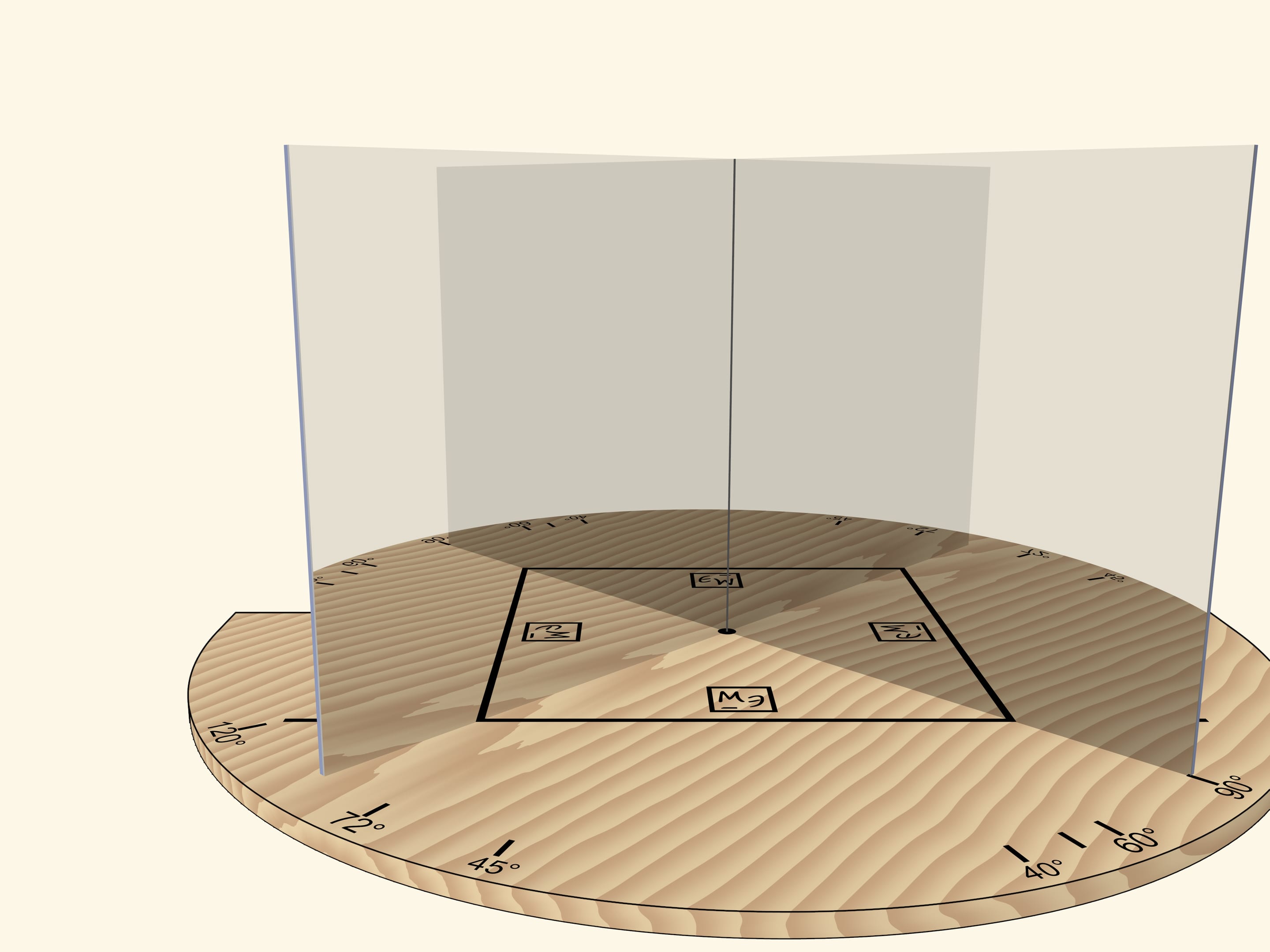
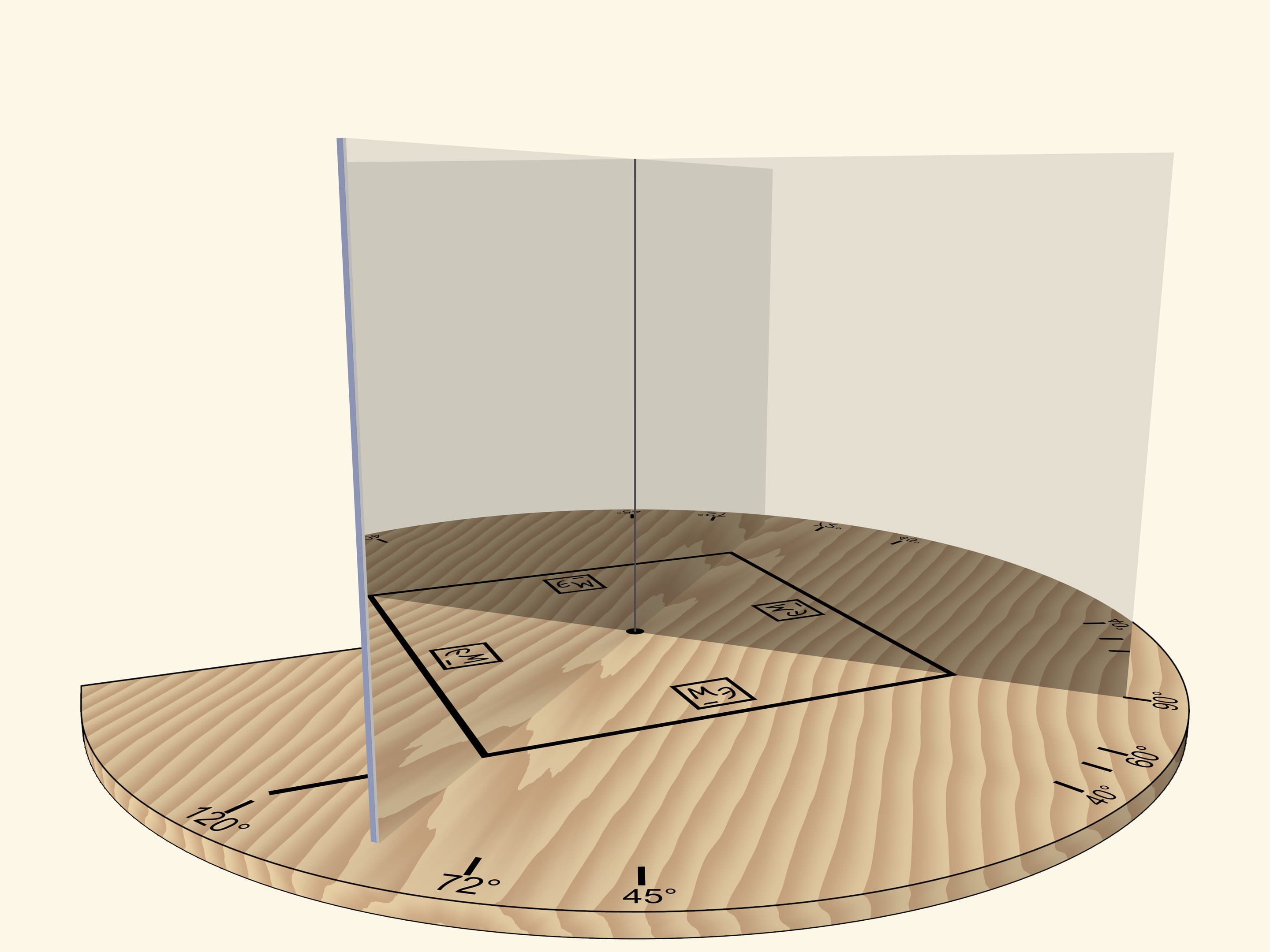
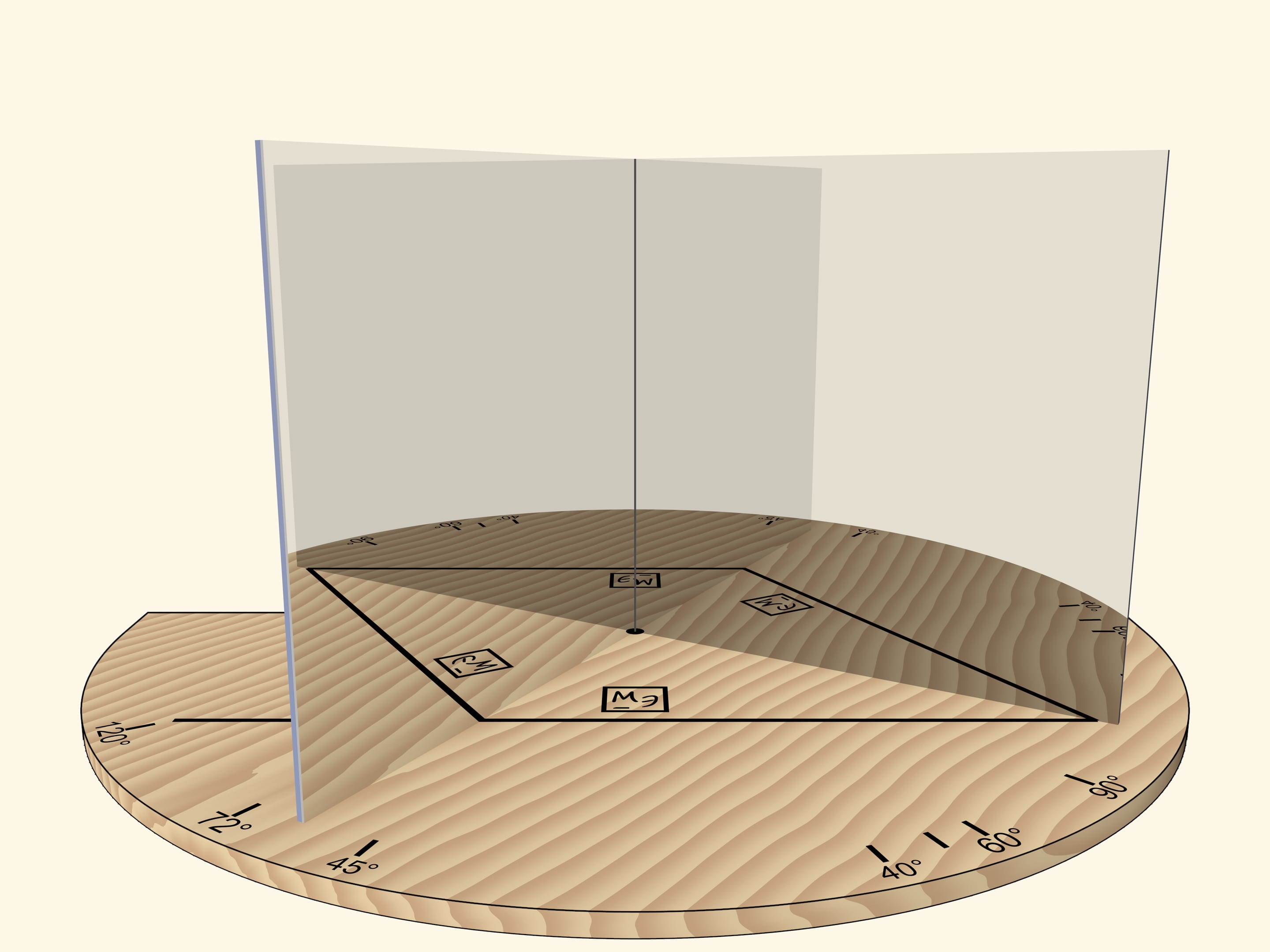
But if we rotate the mirror book as a whole (so that the angle remains right) relative to the base and the segment, the square will turn into a rhombus.
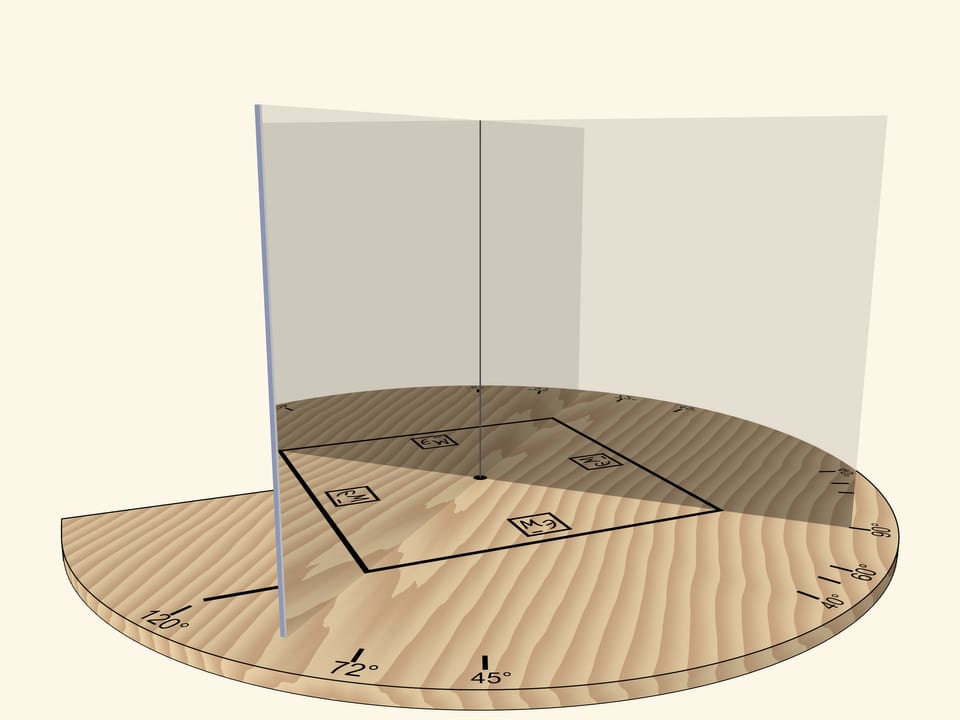
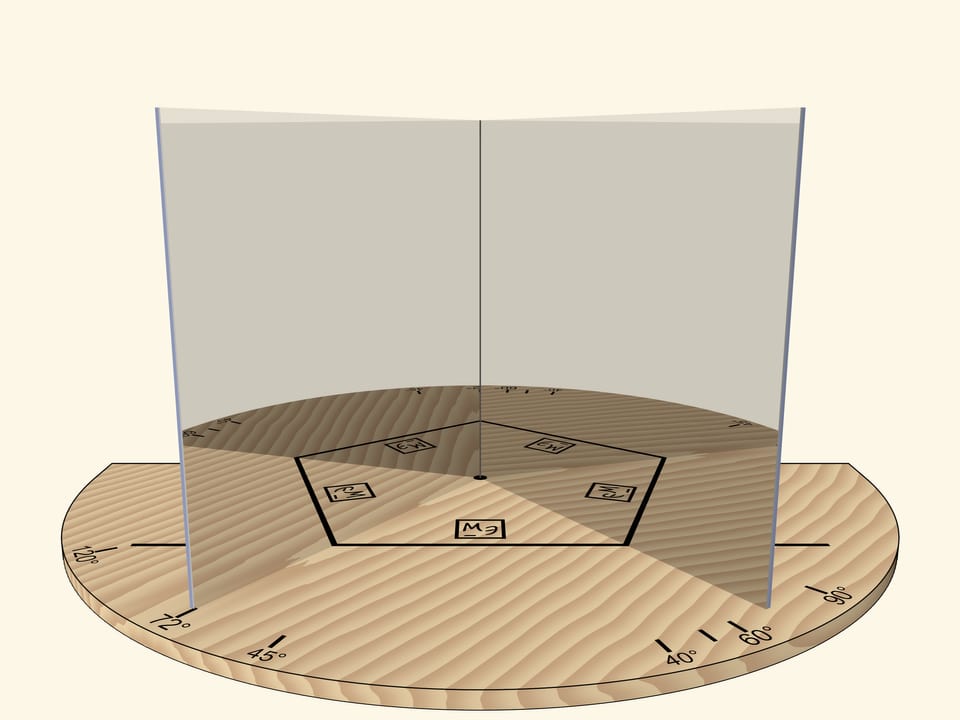
If the angle between mirrors is $72^\circ$, then, as it’s easy to guess, a regular pentagon will be visible in mirrors.
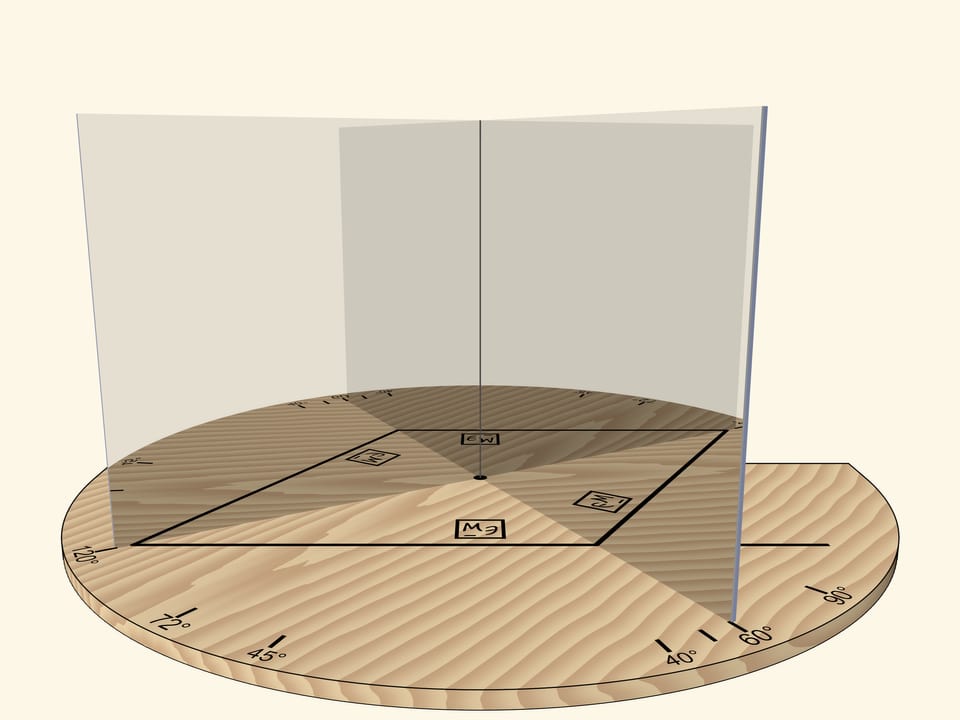
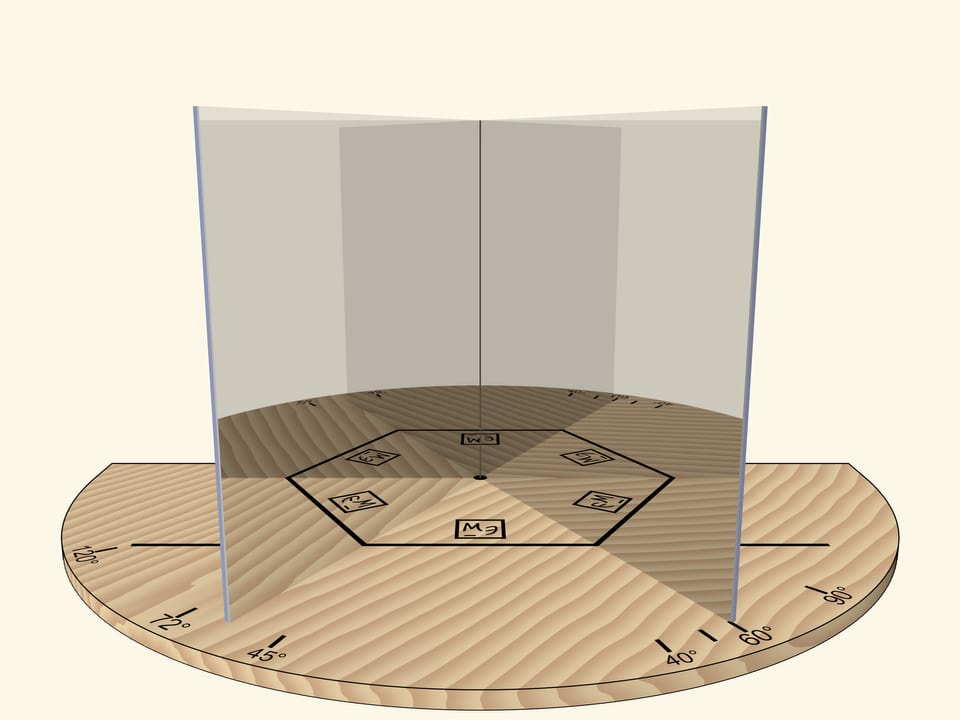
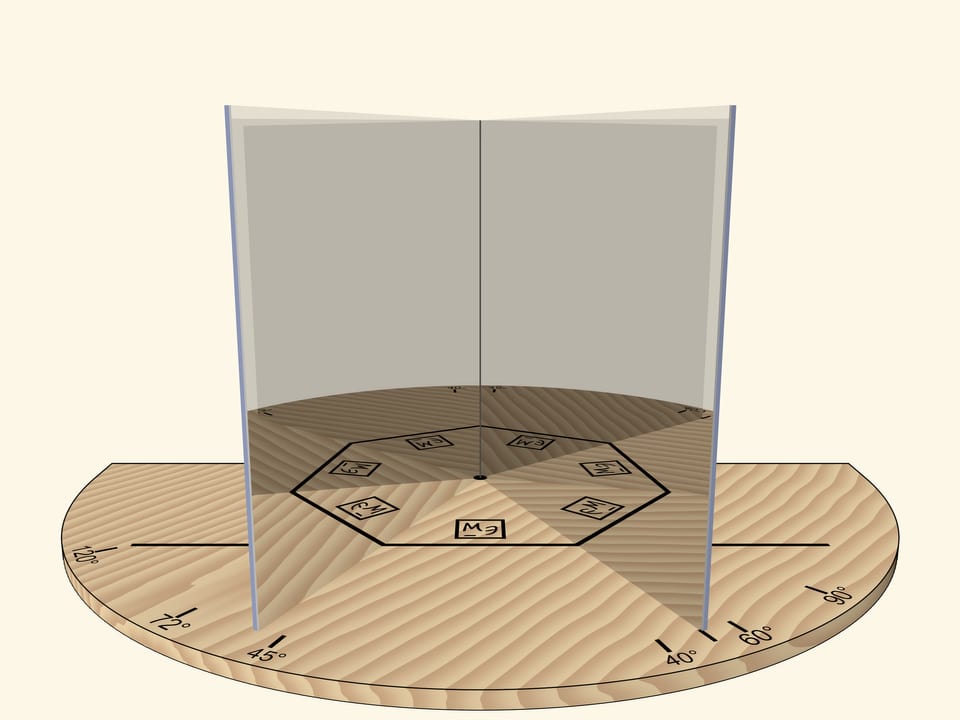
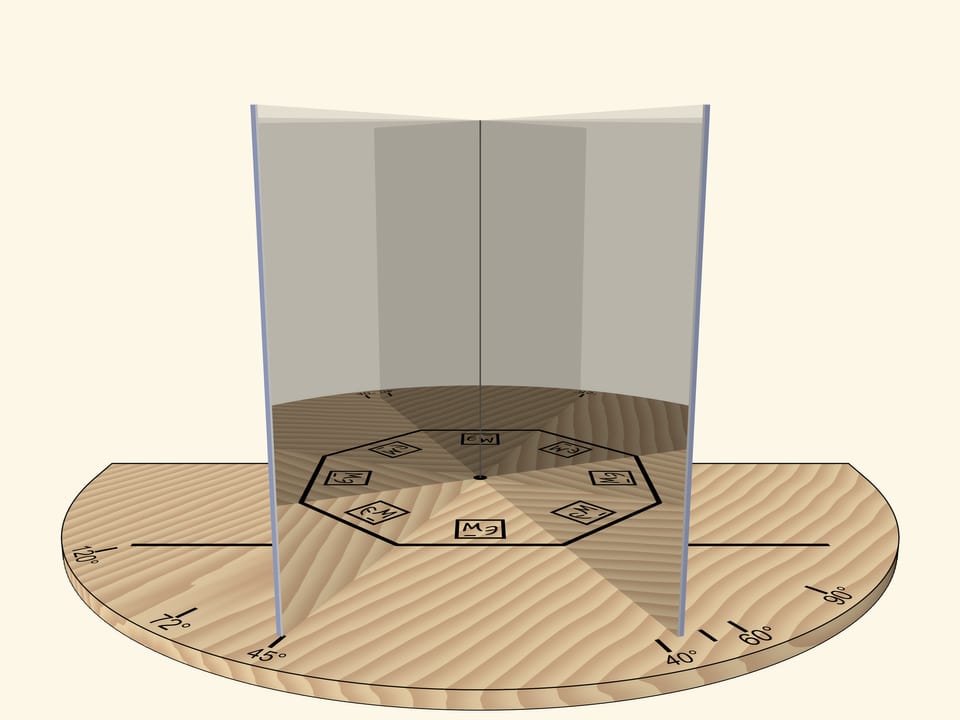
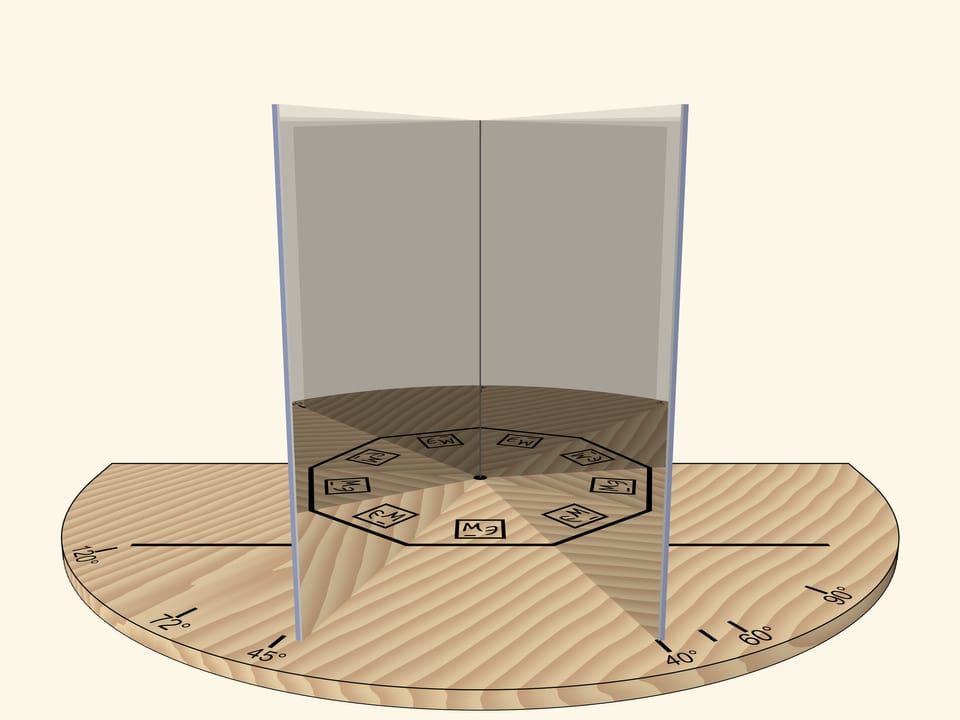
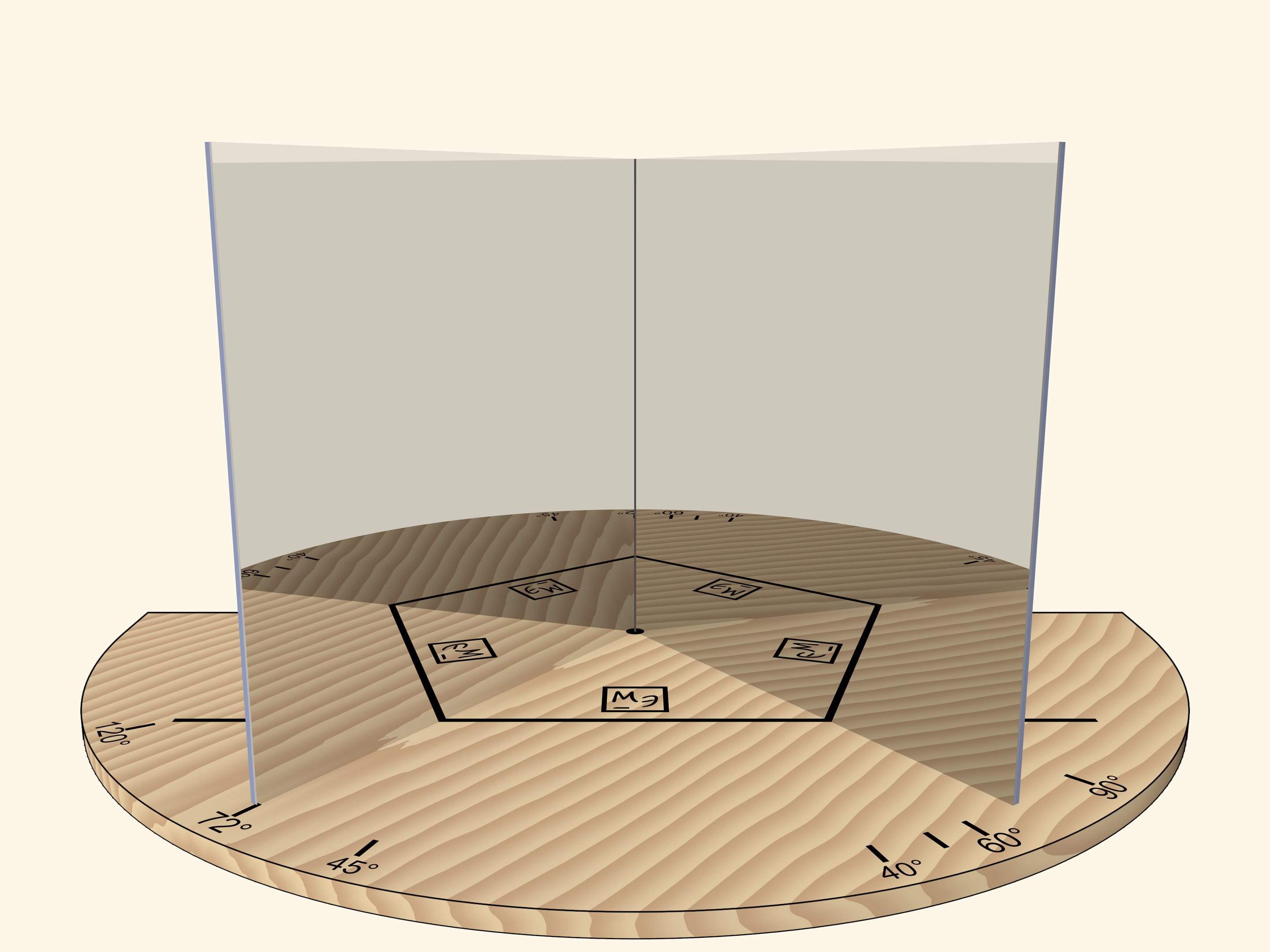
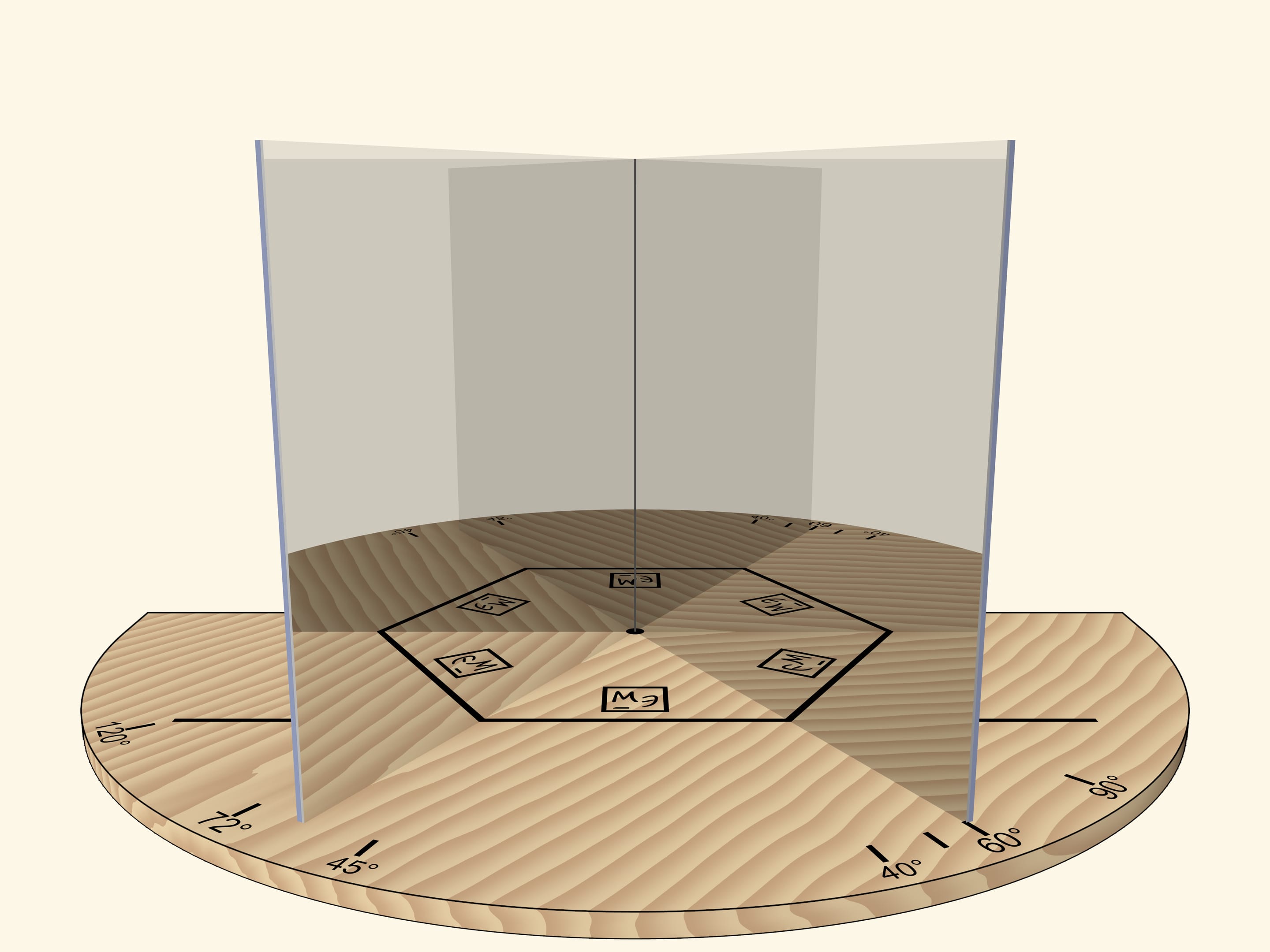
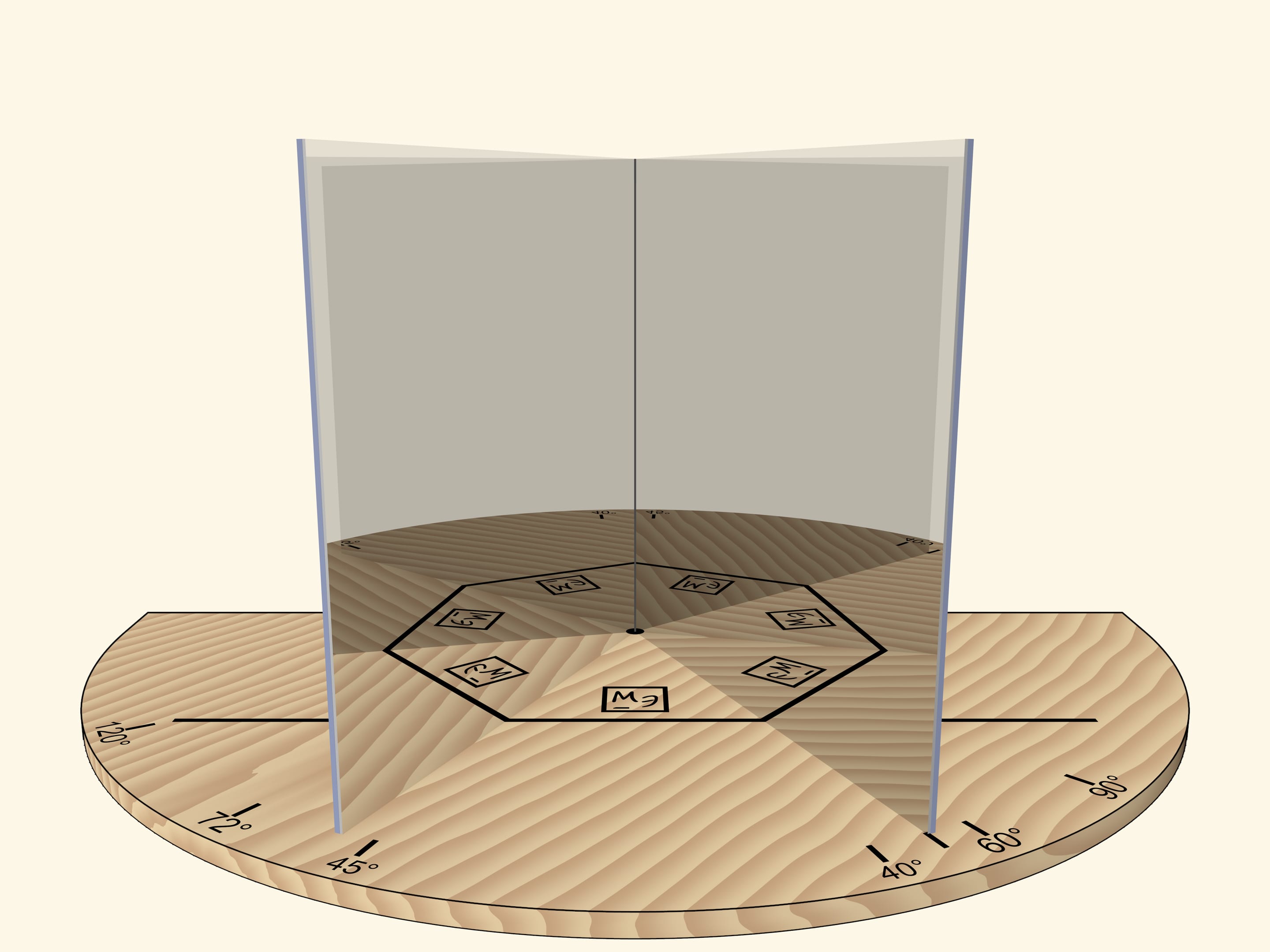
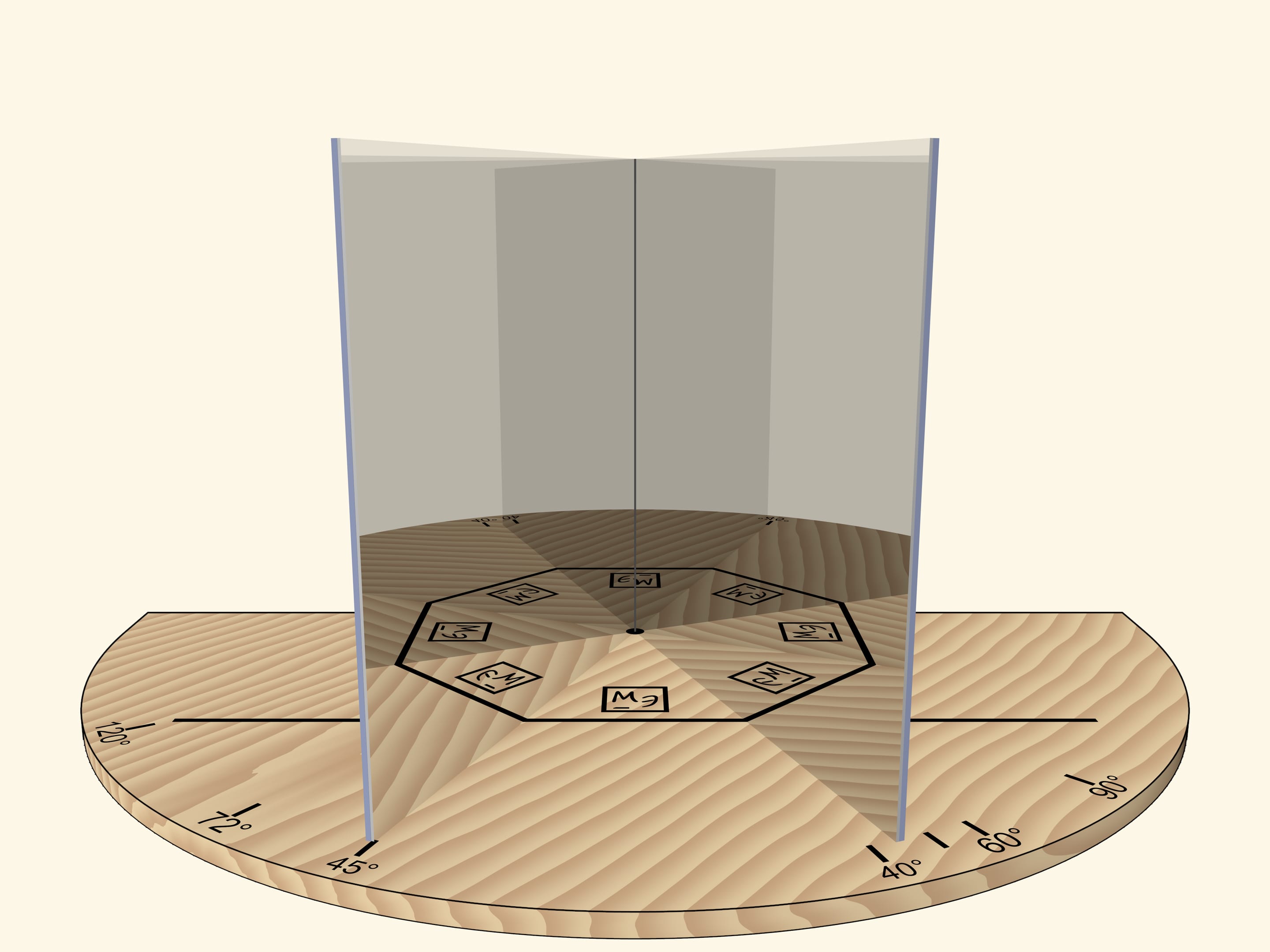
With the angle of $60^\circ$, we’ll get the regular hexagon. If we rotate the mirror book as a whole relative to the base, then at some point we’ll get the regular triangle. Careful observer will notice that the image of the triangle is fundamentally different from the case when the right angle was rotated: the triangle, for sure, is regular, but an image of a logo is not correct.
At the angle of $360^\circ/7$, the reflections group will produce a heptagon.
It’s possible to continue: in every case when the angle between mirrors is $360^\circ/n$, the image in the mirror book will always be a regular n-gon. And the image will always be stable!
But if the angle between the mirrors differs from $360^\circ/n$, then only some fragments of the primary area between mirrors will be visible near the “spine” of the mirror book. If the observer moves relative to the mirrors, these fragments will change — we won’t get a kaleidoscope.
A basis of kaleidoscopes is a physical law, which is well demonstrated by a mirror book: mirror reflection in a mirror again works as a mirror.