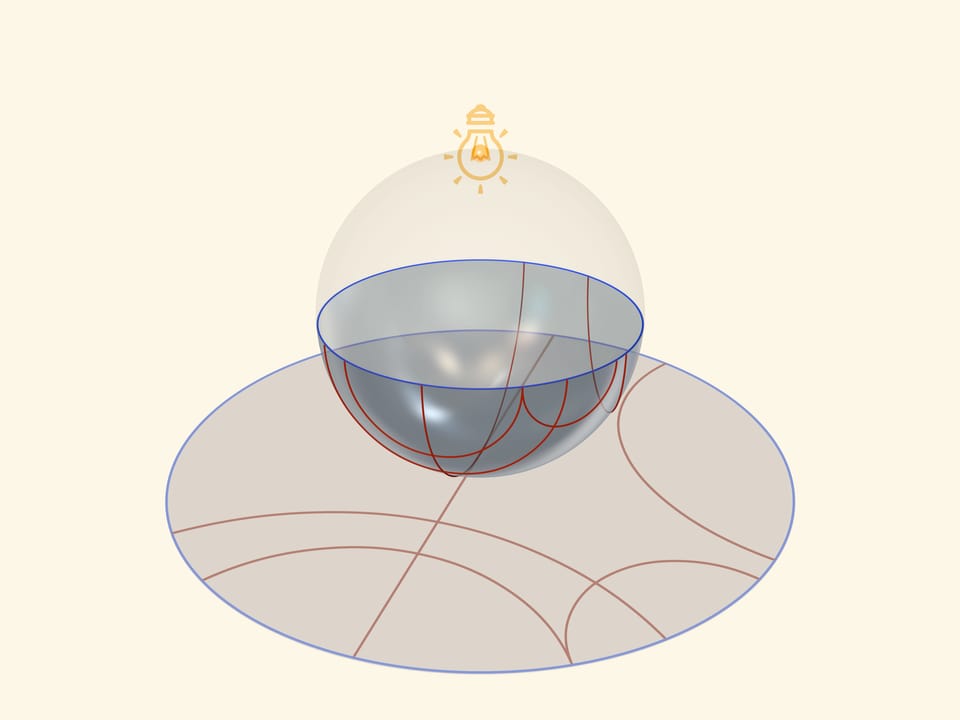
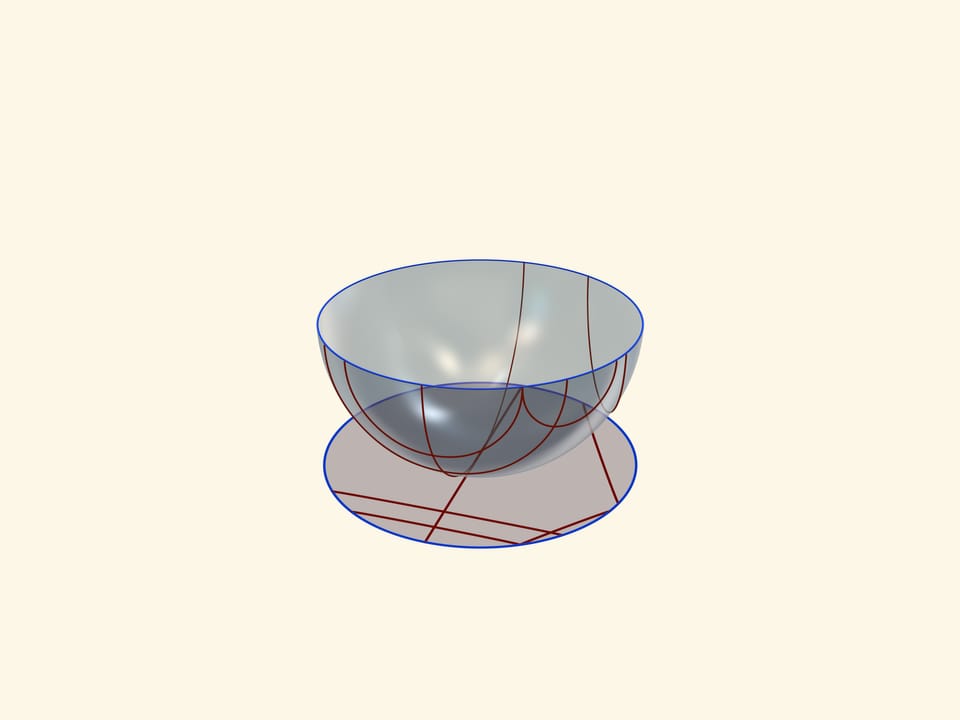
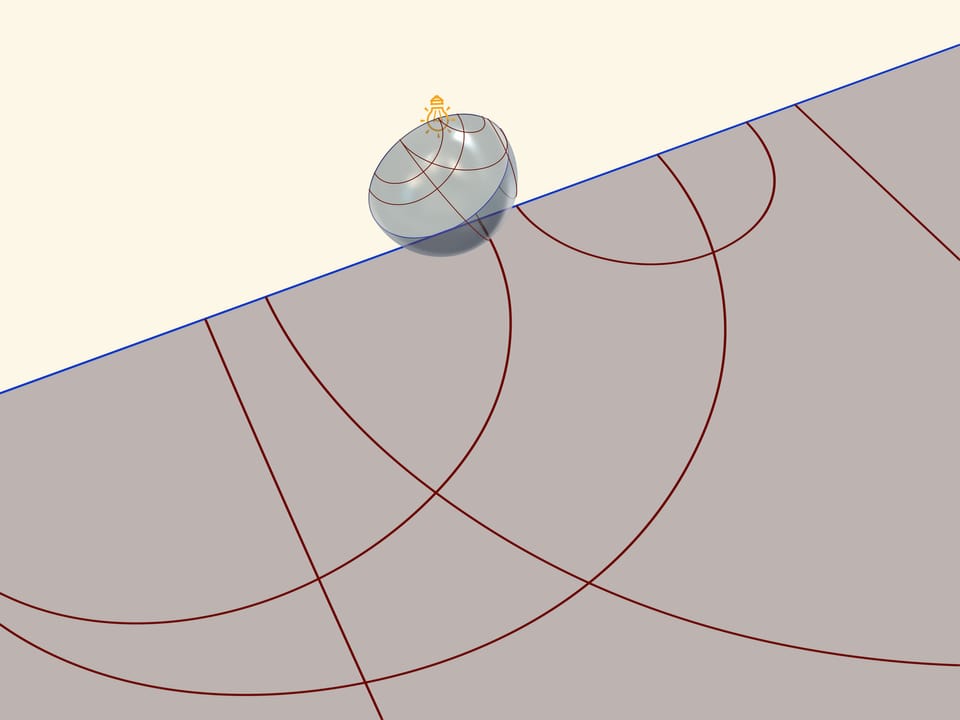
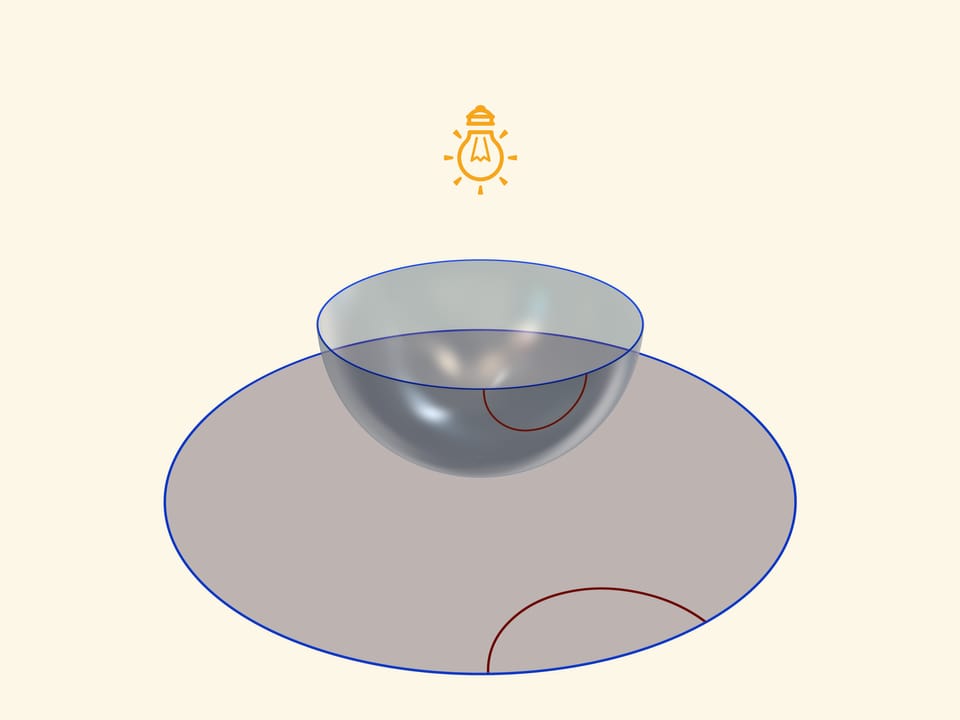
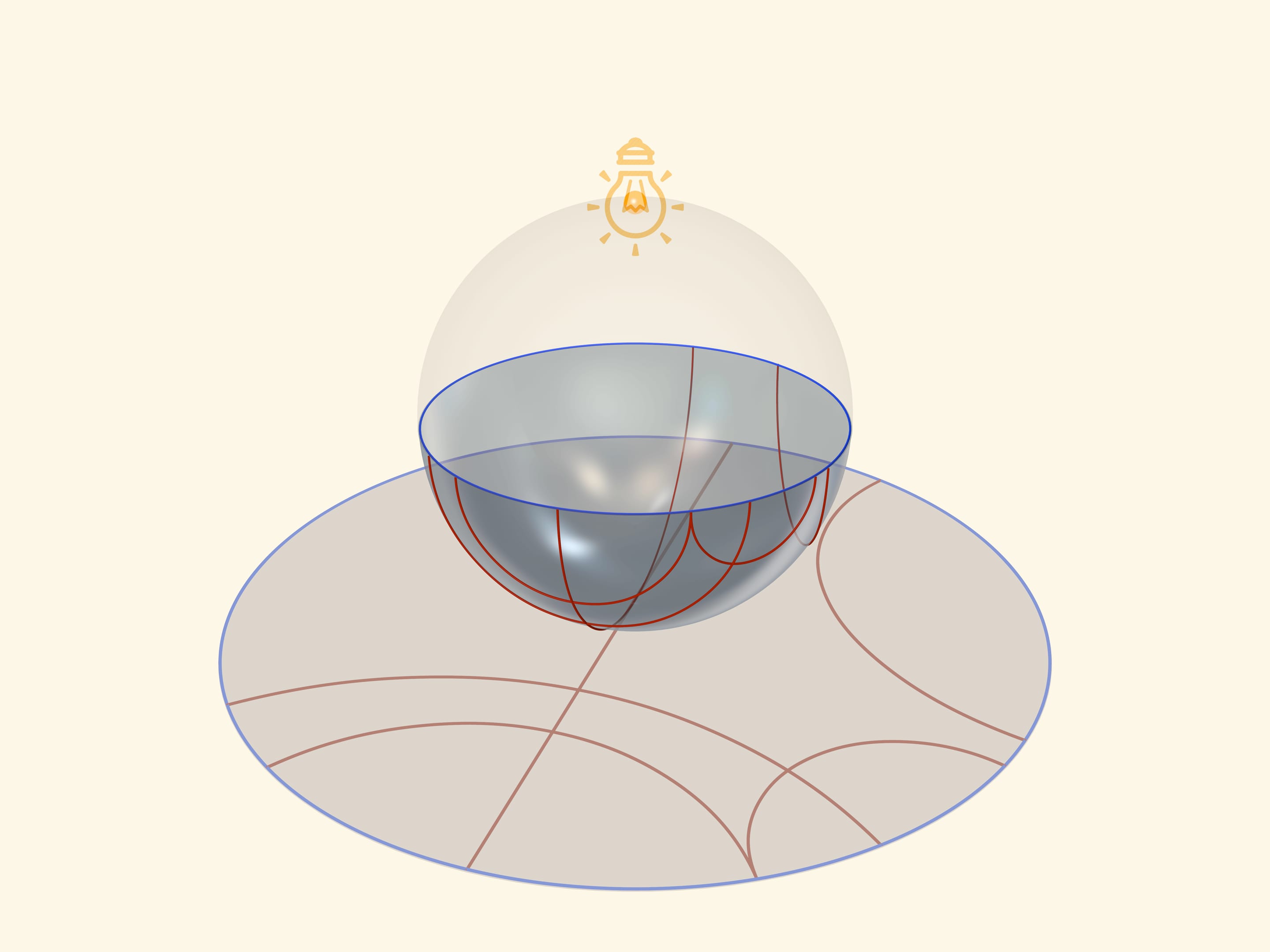
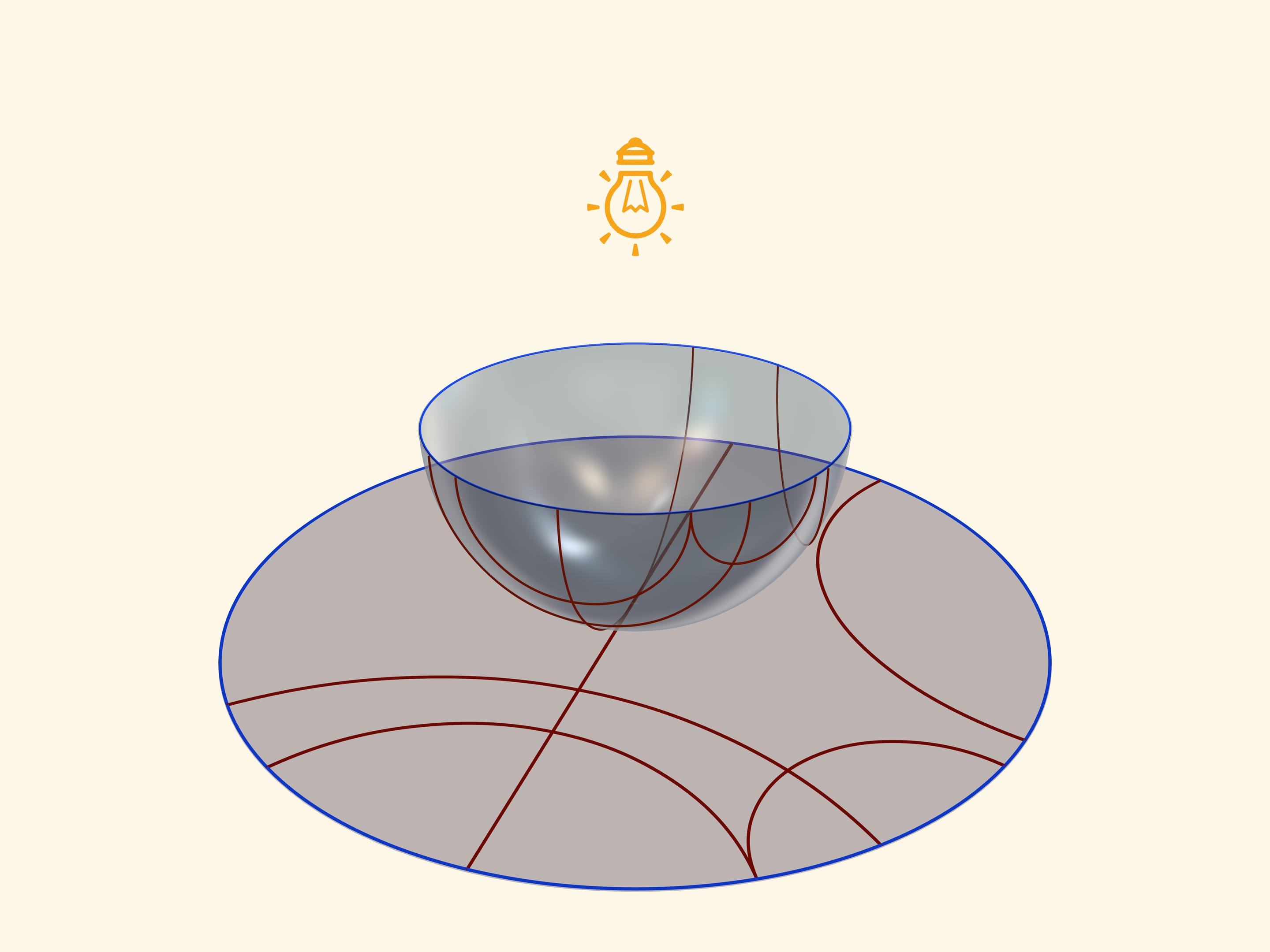
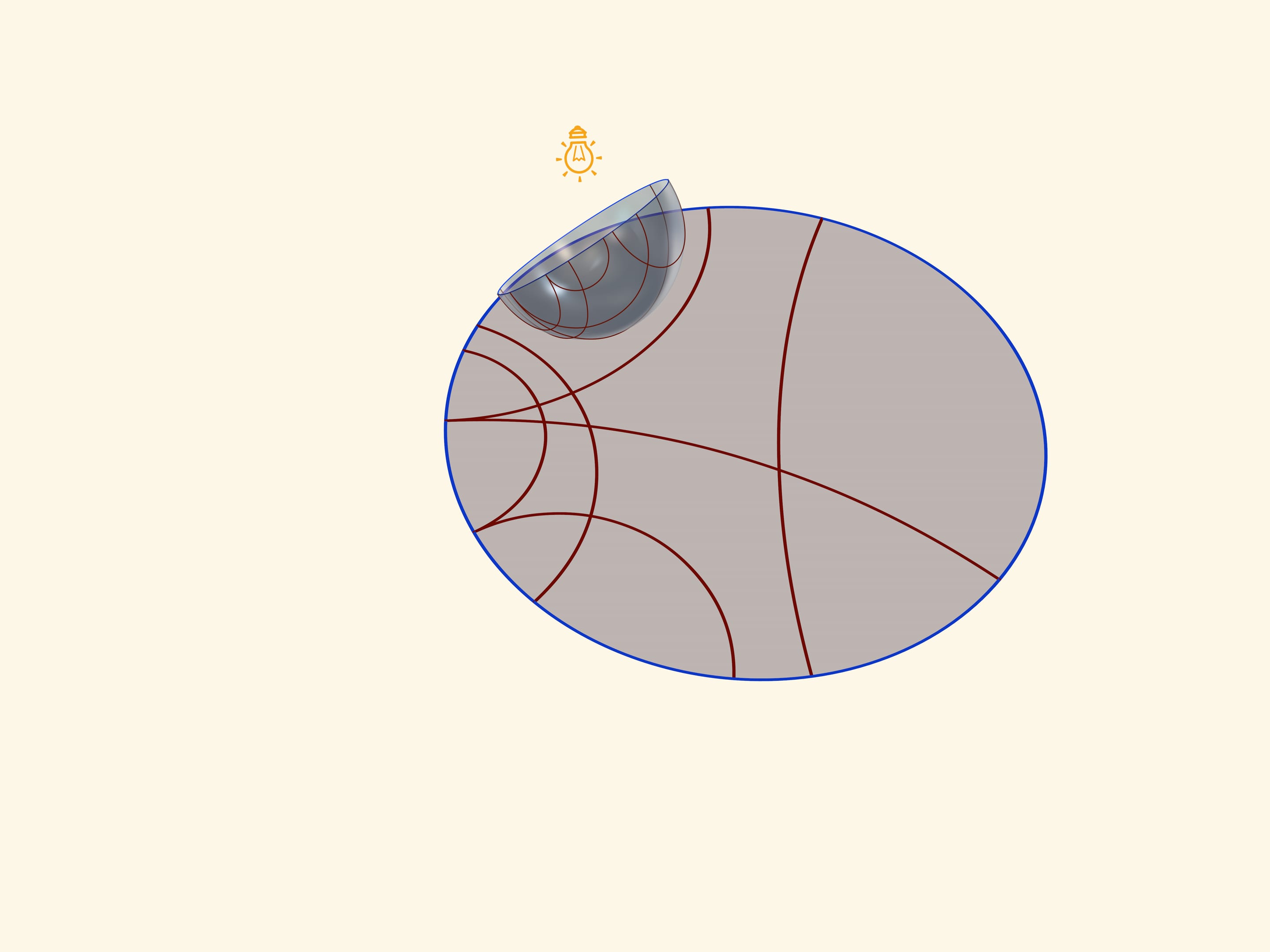
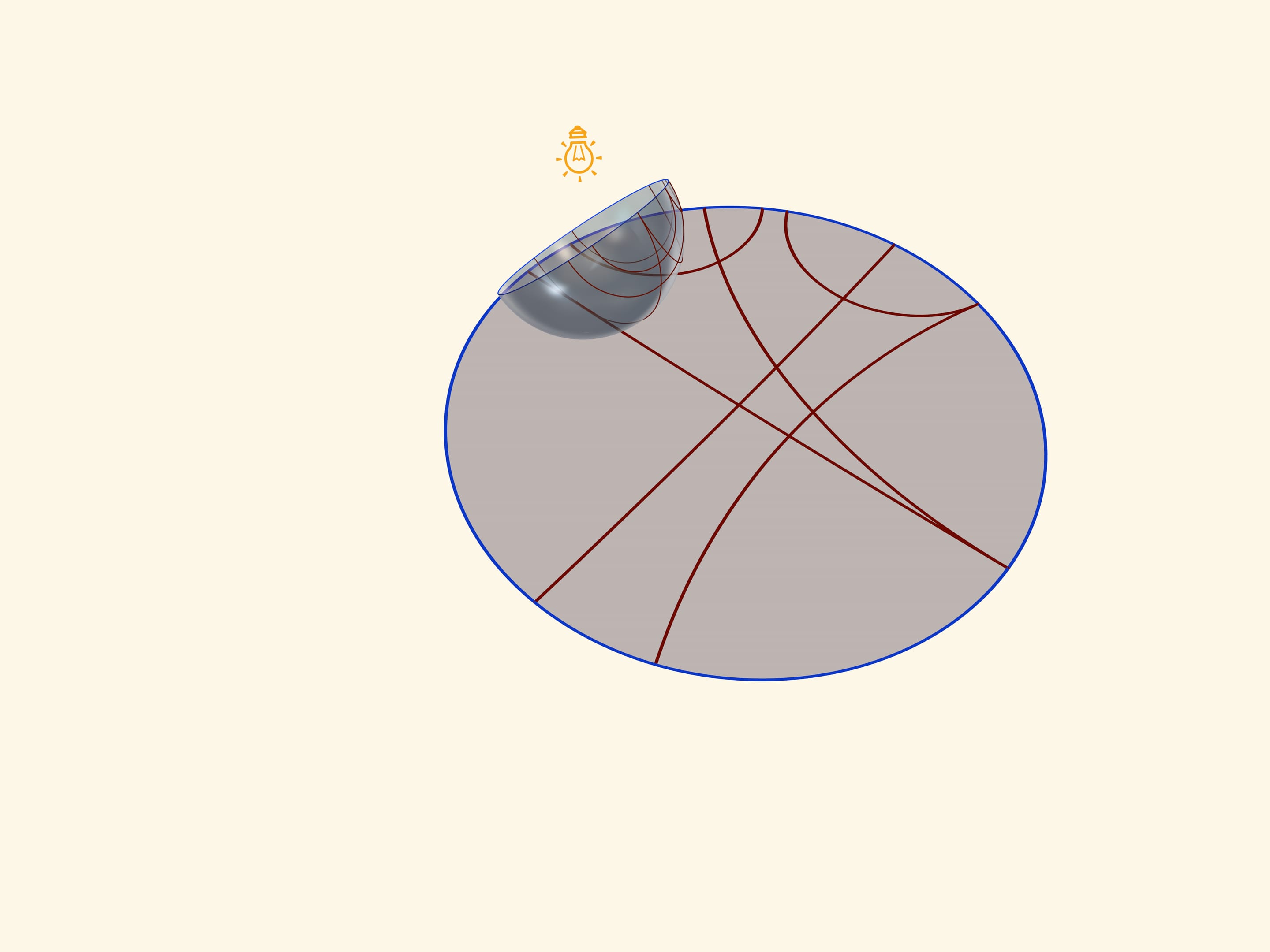
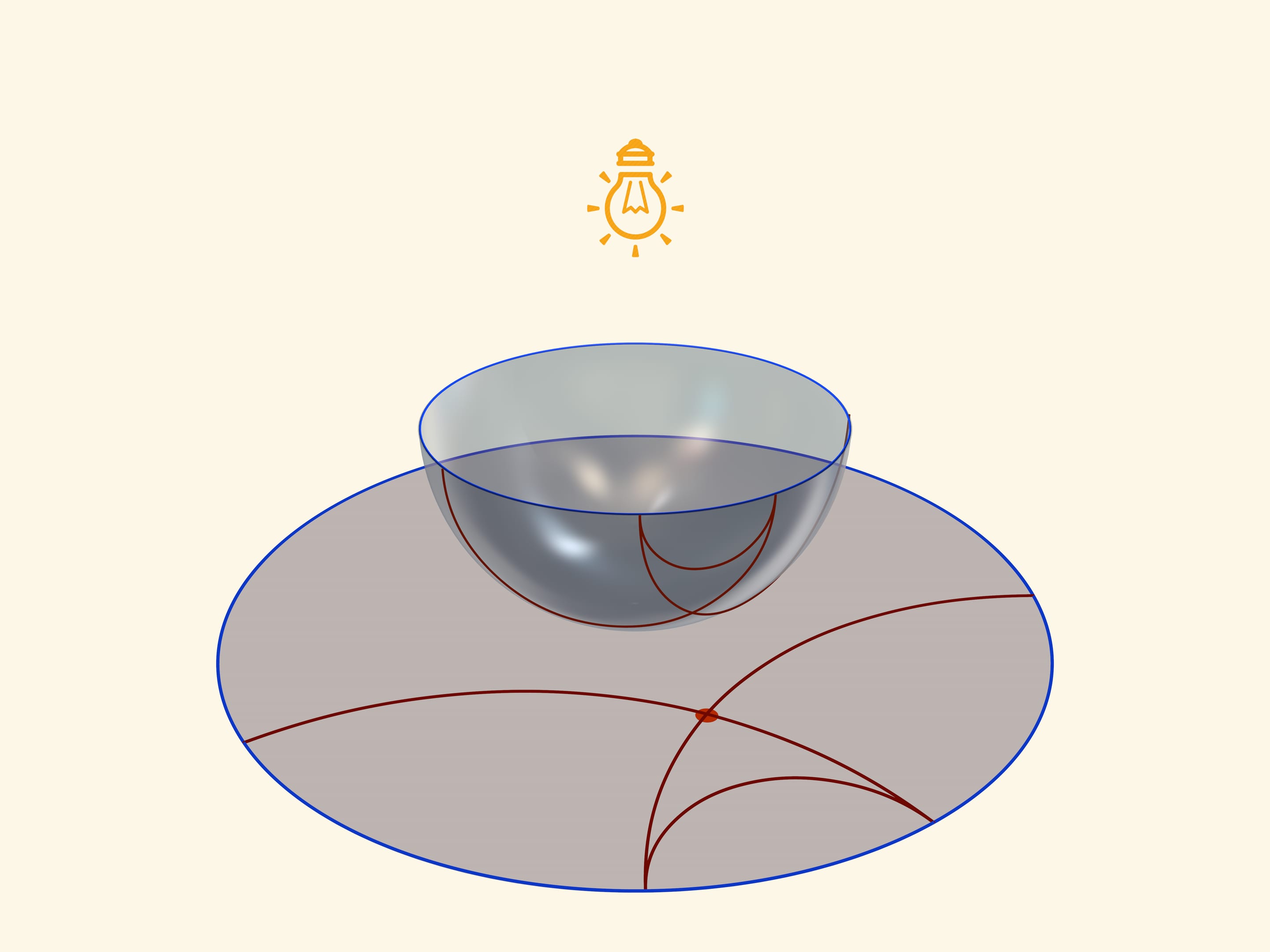
A unique base, which is an image of all three models on a Lobachevsky plane, is a transparent semisphere with semicircles, drawn on it, which are perpendicular to its border-an equator. So if an equator of a semisphere lies in a horizontal plane, a circle should be drawn in vertical planes.
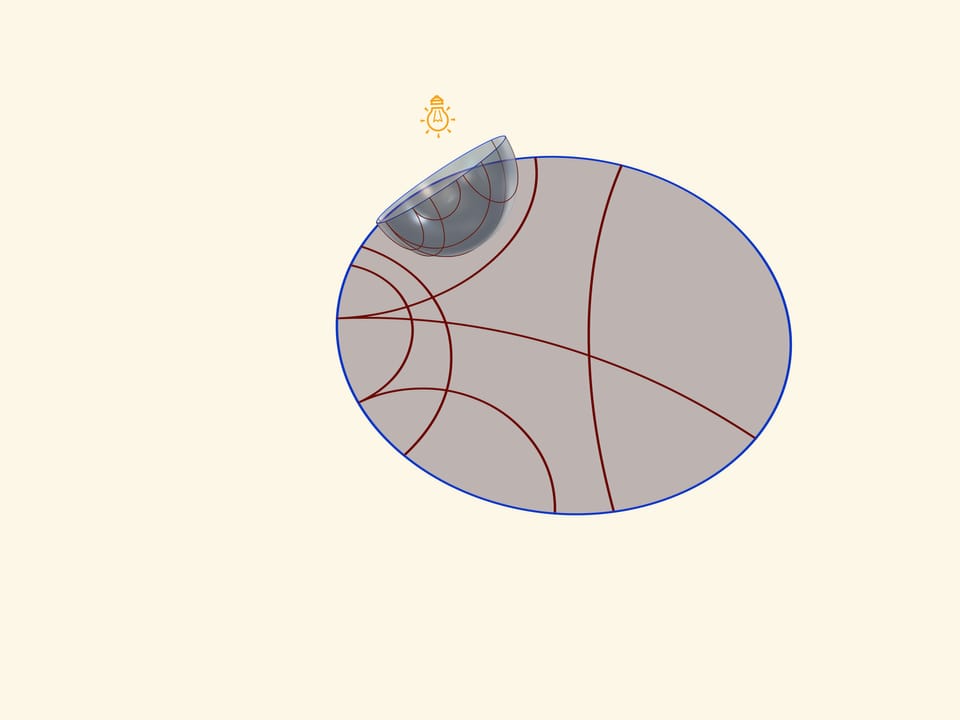
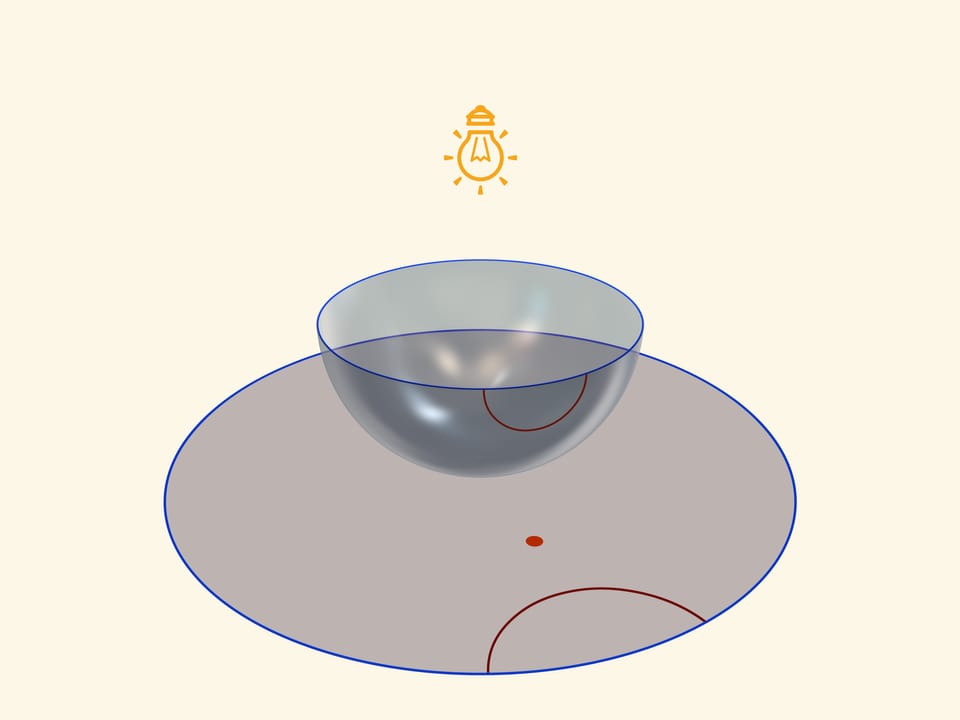
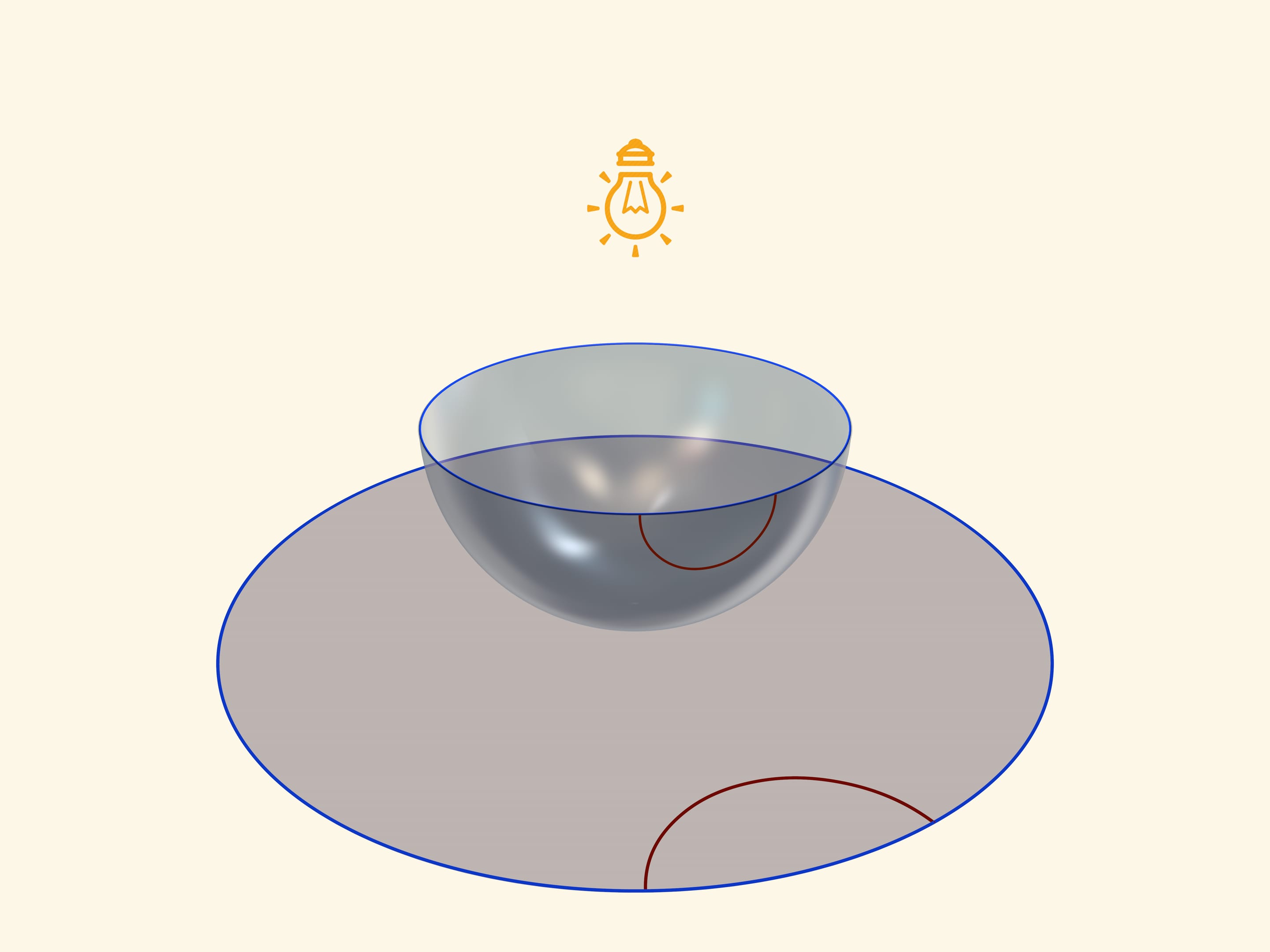
A model of Poincaré in a circle can be received, if one places a semisphere on a table by a pole, and a point source of light ‘in an opposite, Northern pole of a sphere. Taking into consideration that it is a point source, namely rays disperse from it on straight lines to different sides, one receives a stereographic projection of the sphere (in our case semisphere) on the plane. A stereographic projection saves angles between lines, and turns any circles on the sphere into circles on a plane. (To be more precise, circles, which don’t pass through the centre of a projection, pass to circles on the plane, and those, that pass through it-to straight lines).
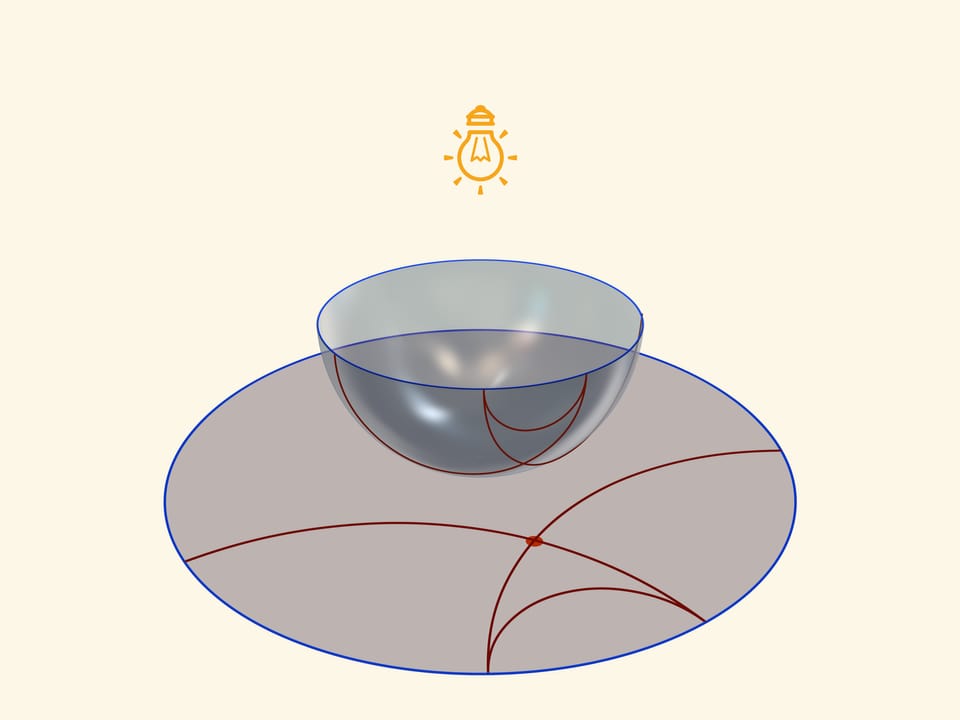
An equator of a semisphere turns into an absolute on a Lobachevsky plane (its points don’t belong to it), which is a border of a Poincaré’s model in a circle. Circles on a semisphere, perpendicular to an equator, turn into circles in a circle, perpendicular to absolute. Namely they are “straight lines” on Lobachevsky plane.
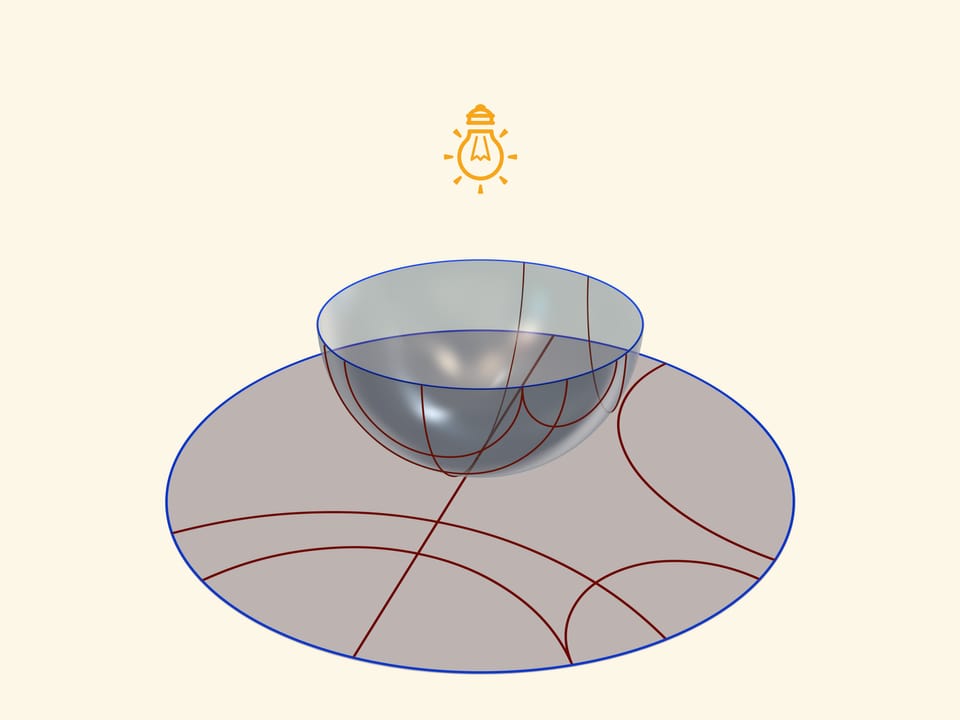
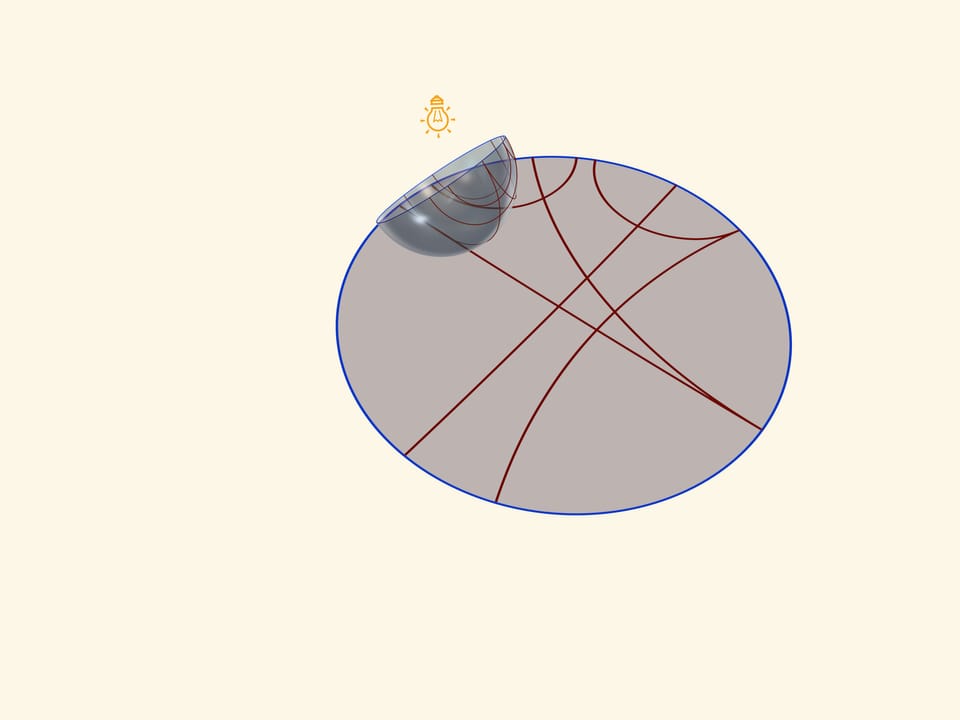
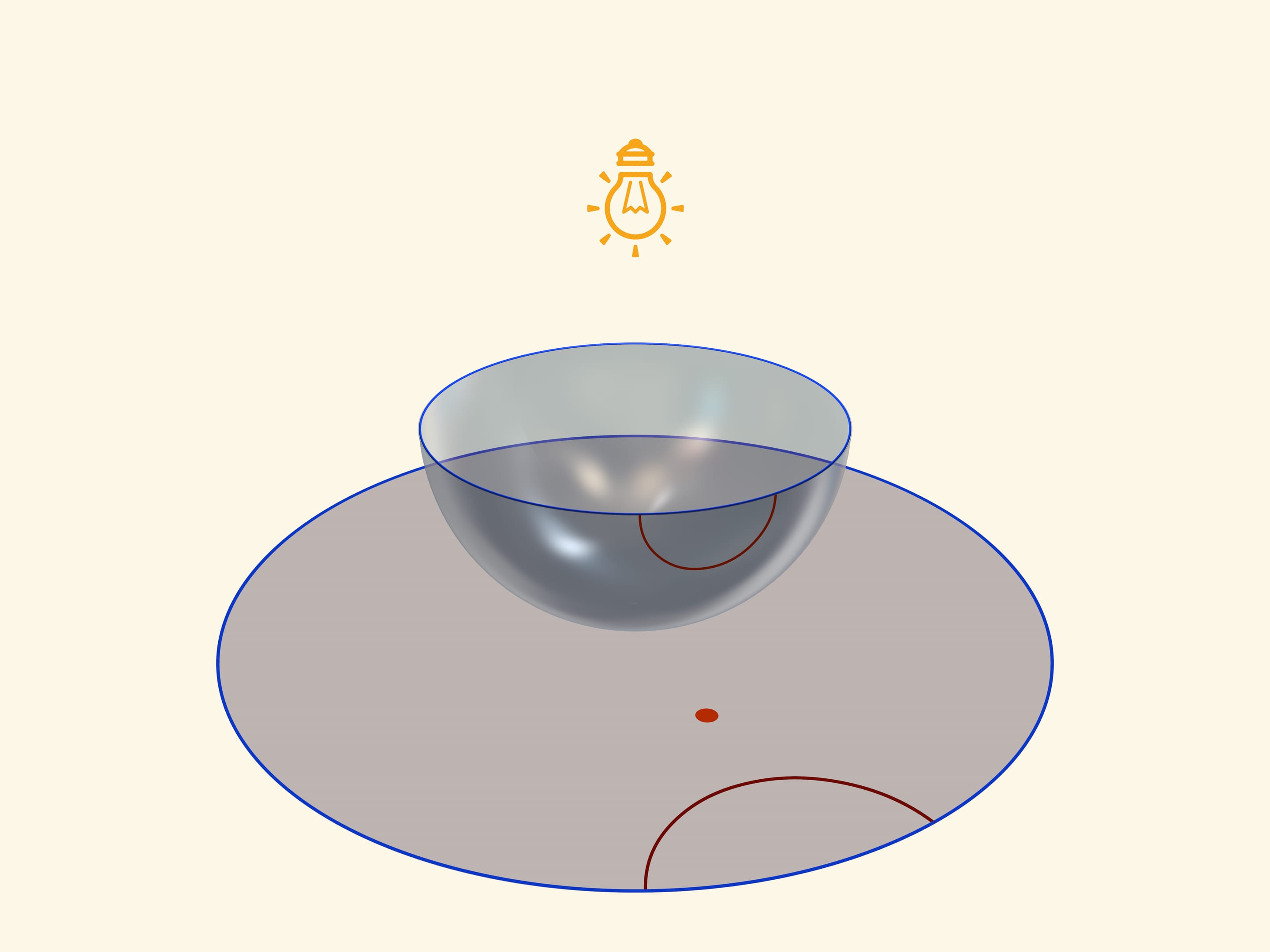
A model of Beltrami-Klein in a circle (a projective model) will be created, if in case of the same position of a semisphere a source of light will be “ran into“, namely will lighten a semisphere by vertical parallel rays. An absolute will be a projection of an equator, and straight planes of Lobachevsky are hordes of a circle. A projection of equator will be an absolute, and straight planes of Lobachevsky are hordes of a circle.
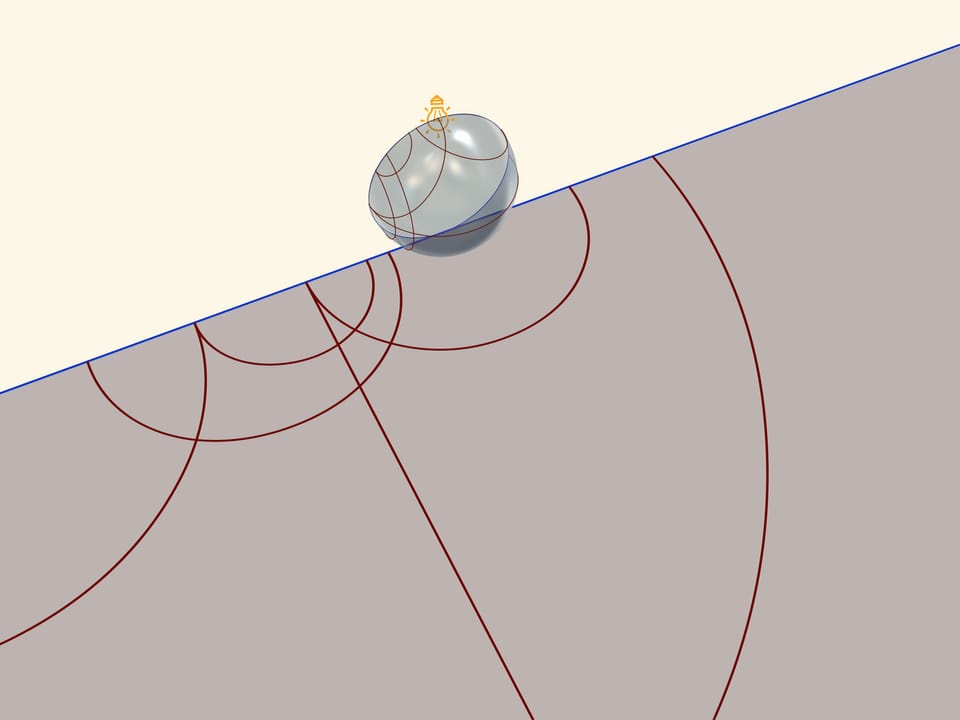
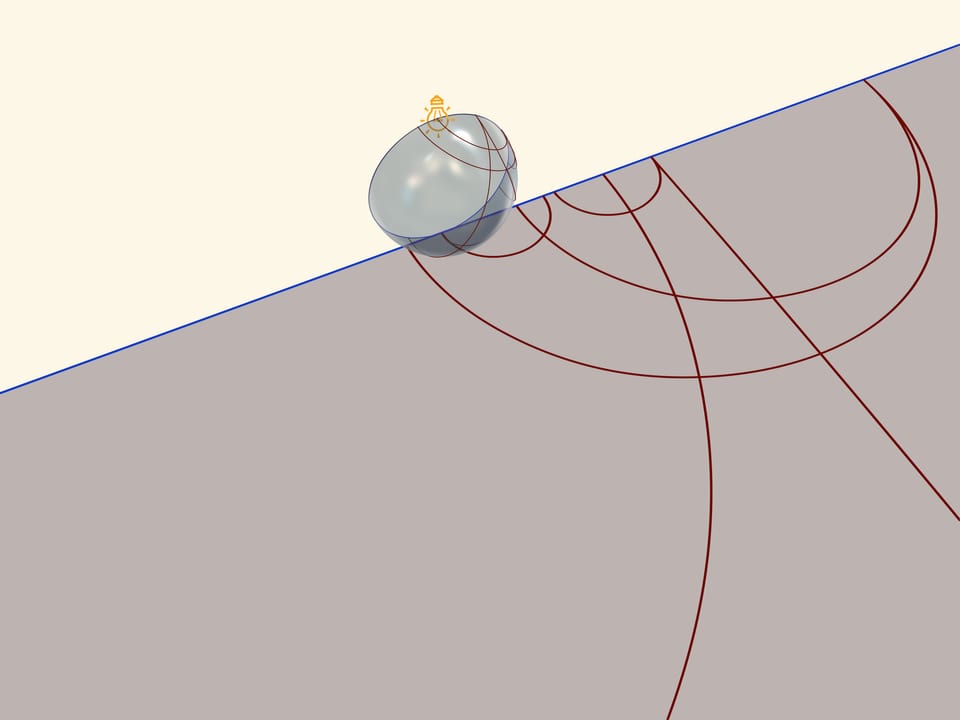
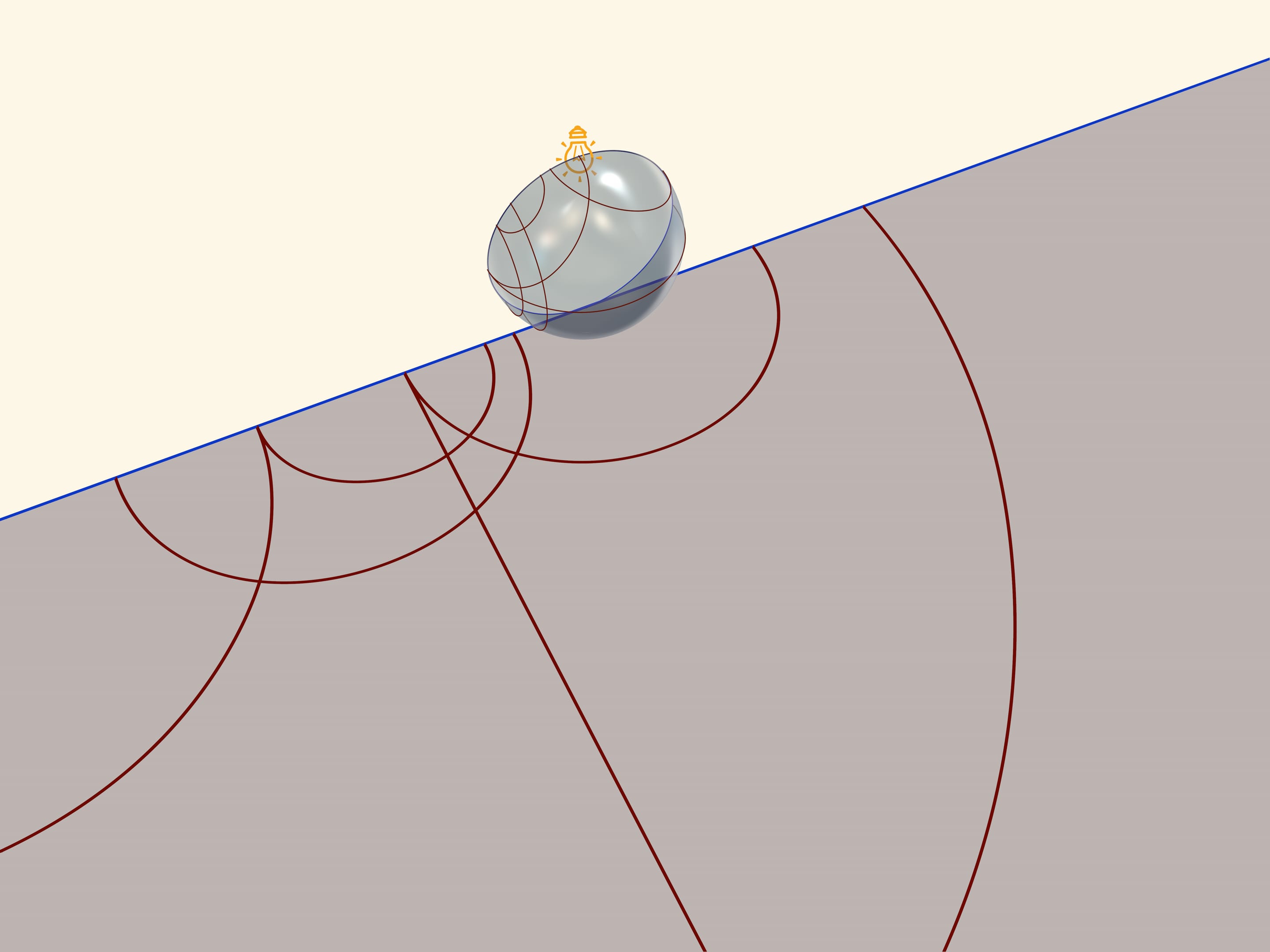
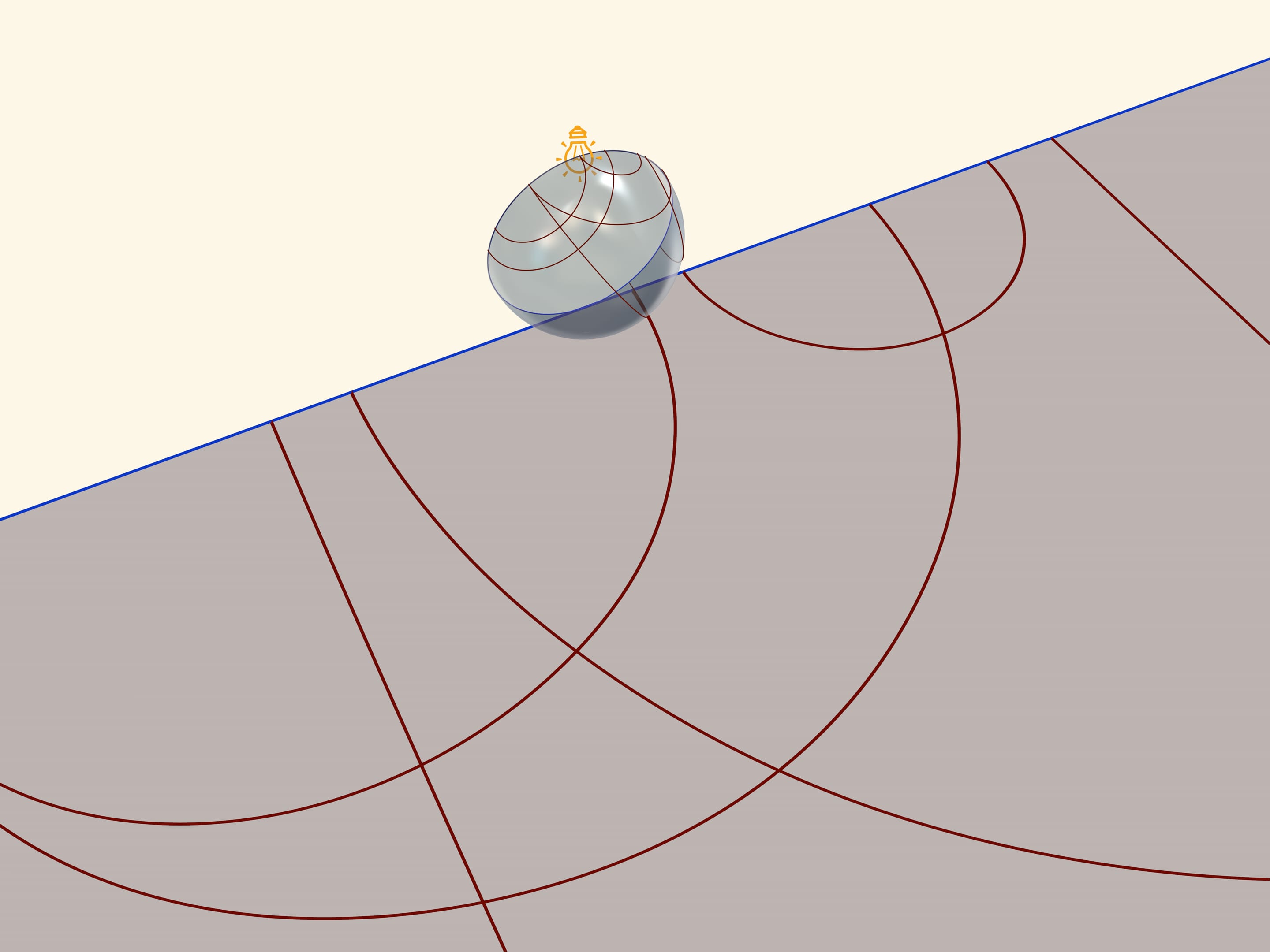
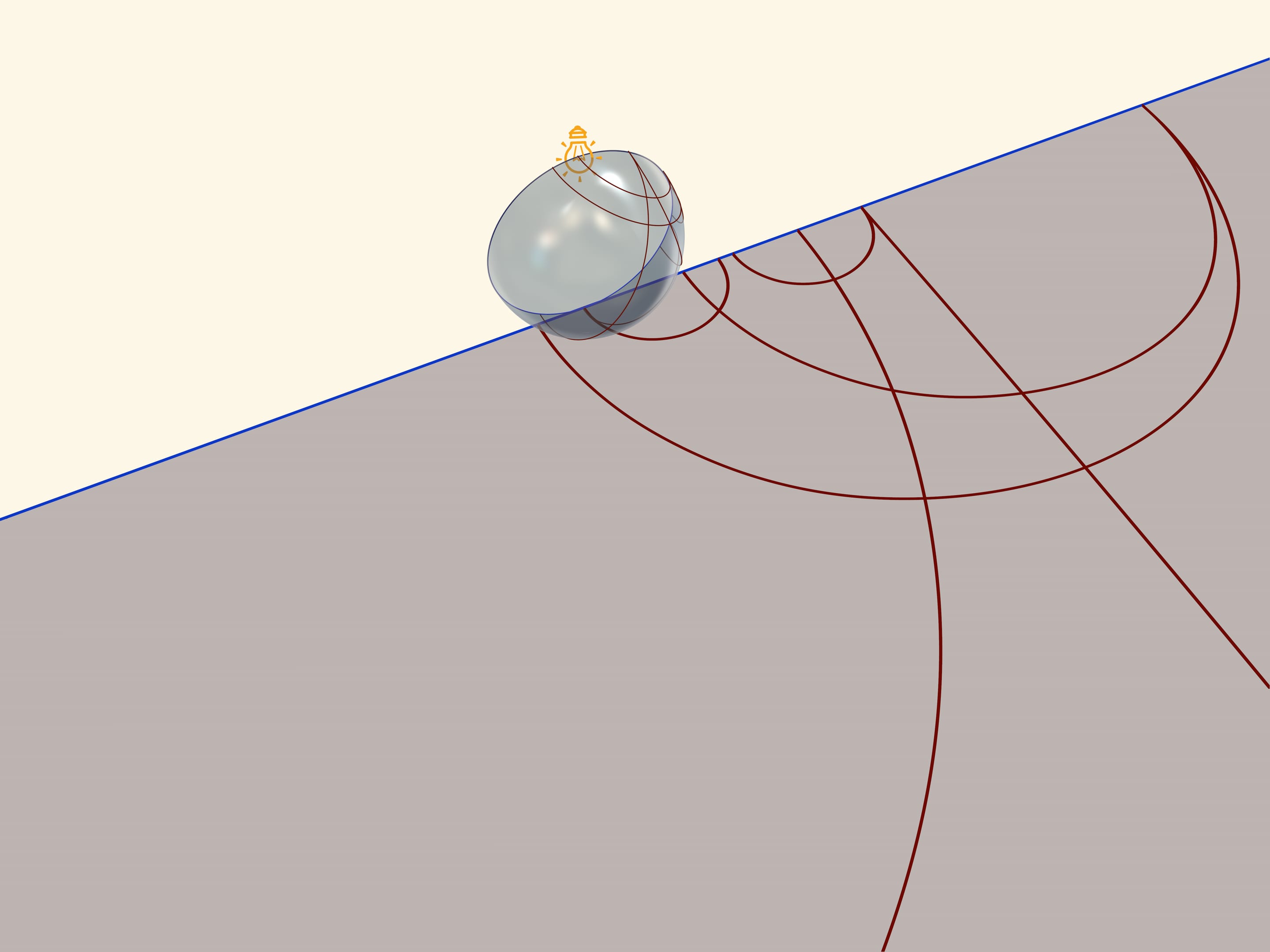
A model of Poincaré on a semiplane can be received, if a semisphere is settled on a table so that its equator is in a vertical plane, and source of light-in the North Pole. stenographic projection, where a semisphere is projected in a plane and an equator of a semisphere goes into a straight line, arouses again, - an absolute of Lobachevsky’s plane in this model. Straight lines in Poincaré’s model in a semiplane will be circles and straight lines, perpendicular to an absolute,-projections from a semisphere of circles, which pass through the North Pole.
If one rotates a semisphere, one can observe transformations (movements) of Lobachevsky plane. In case of Poincaré model on a semiplane a semisphere should be rotated around the axis (so that the equator is always located in the same plane). Transformations (for readers-elliptic) planes of Lobachevsky in case the Poincaré model can be observed, if we rotate a semisphere around the axis, bending it to a vertical line, which join the source of light and tangency point of semisphere and plane of projection. (In case of this position of a semisphere a stereographic projection is received again. Its listed qualities guarantee, that in this case a model of Poincaré in a circle is also received).
Straight planes of Lobachevsky, which pass through one point and are parallel to the given line, are constructed according to the model of Poincaré in a circle. For the fixed circle on a semisphere, for the chosen points two circles that arise from different ends of the fixed one, can be made. As only circles, perpendicular to an equator, are drawn, their projections-straight planes of Lobachevsky-go out of “common” points on the absolute, perpendicular to it (remember that points of an absolute are not involved in tha Lobachevsky plane). It means that any of newly constructed straight lines is parallel to the fixed one. And any straight line, which passes through the chosen point and lies “between” the constructed ones, is called “divergent” with the given one and also doesn’t have common points with it