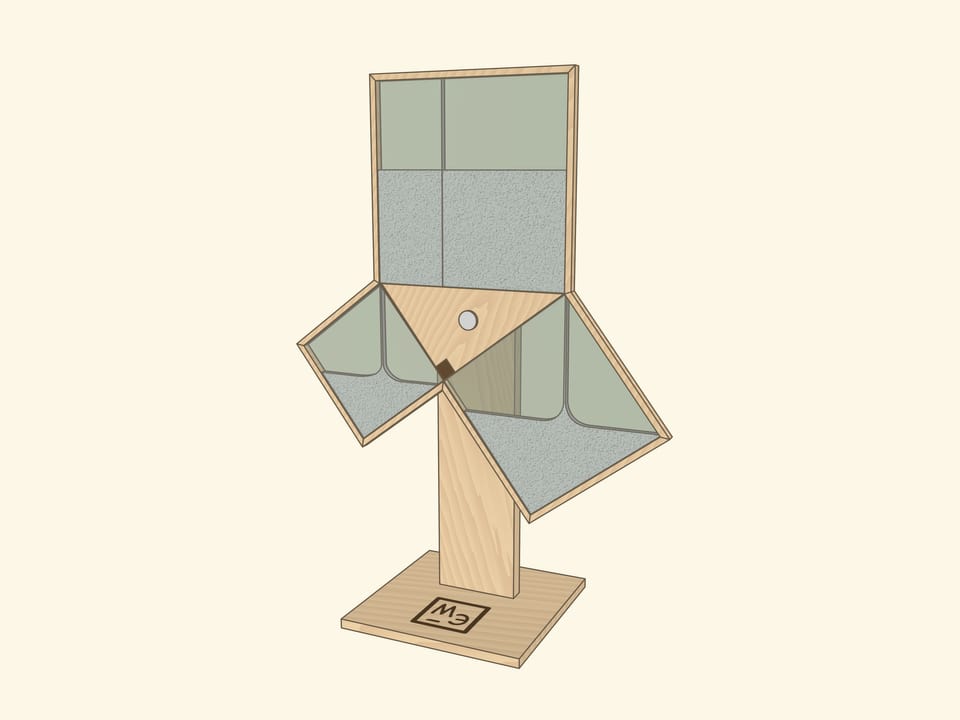
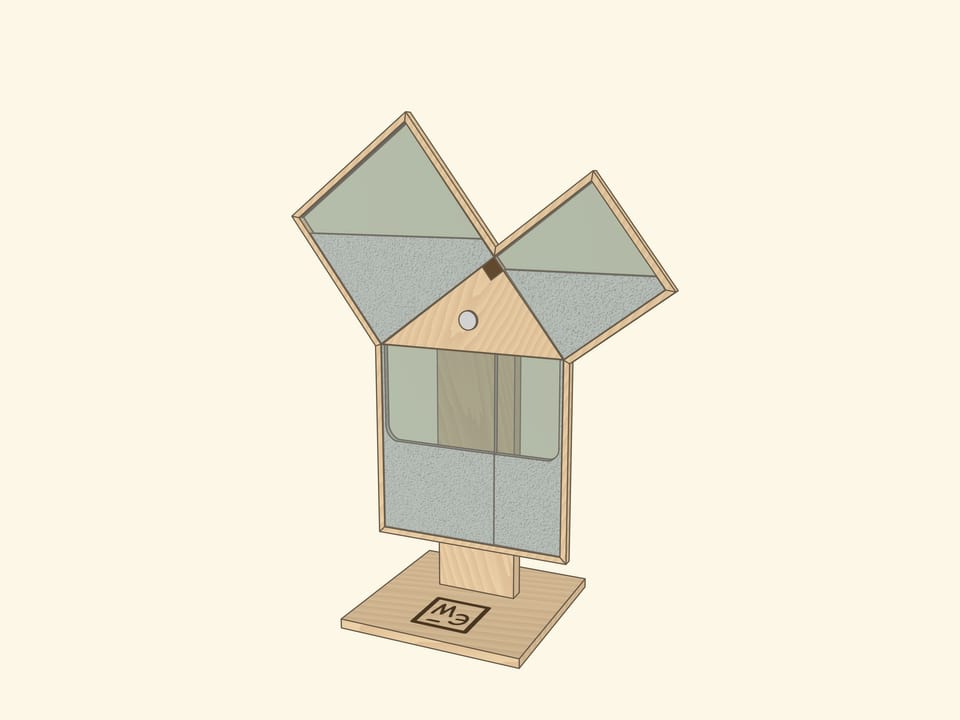
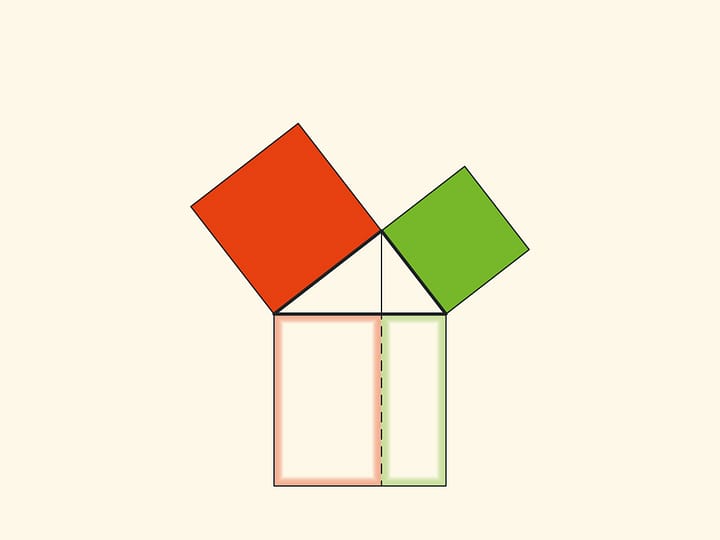
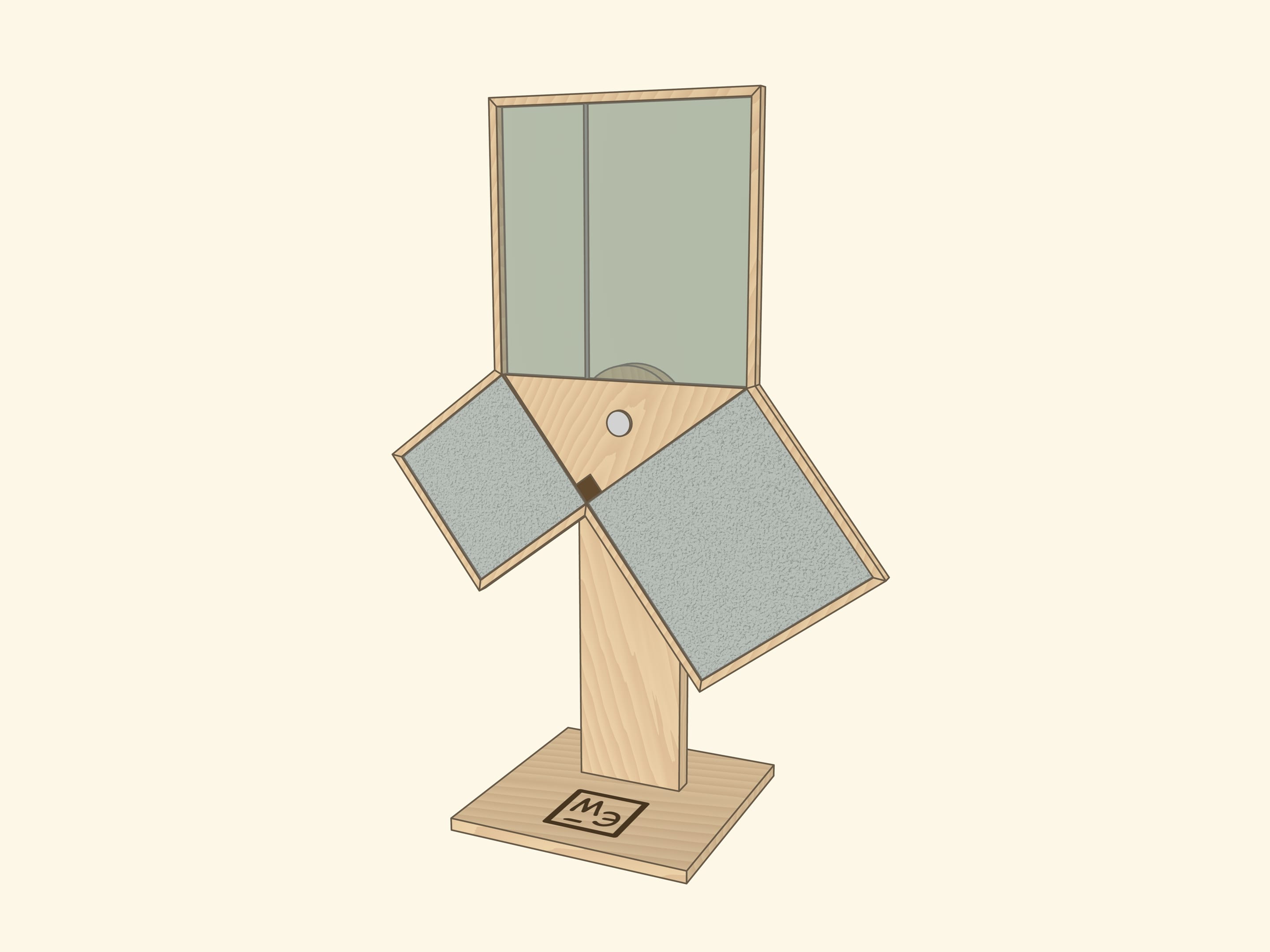
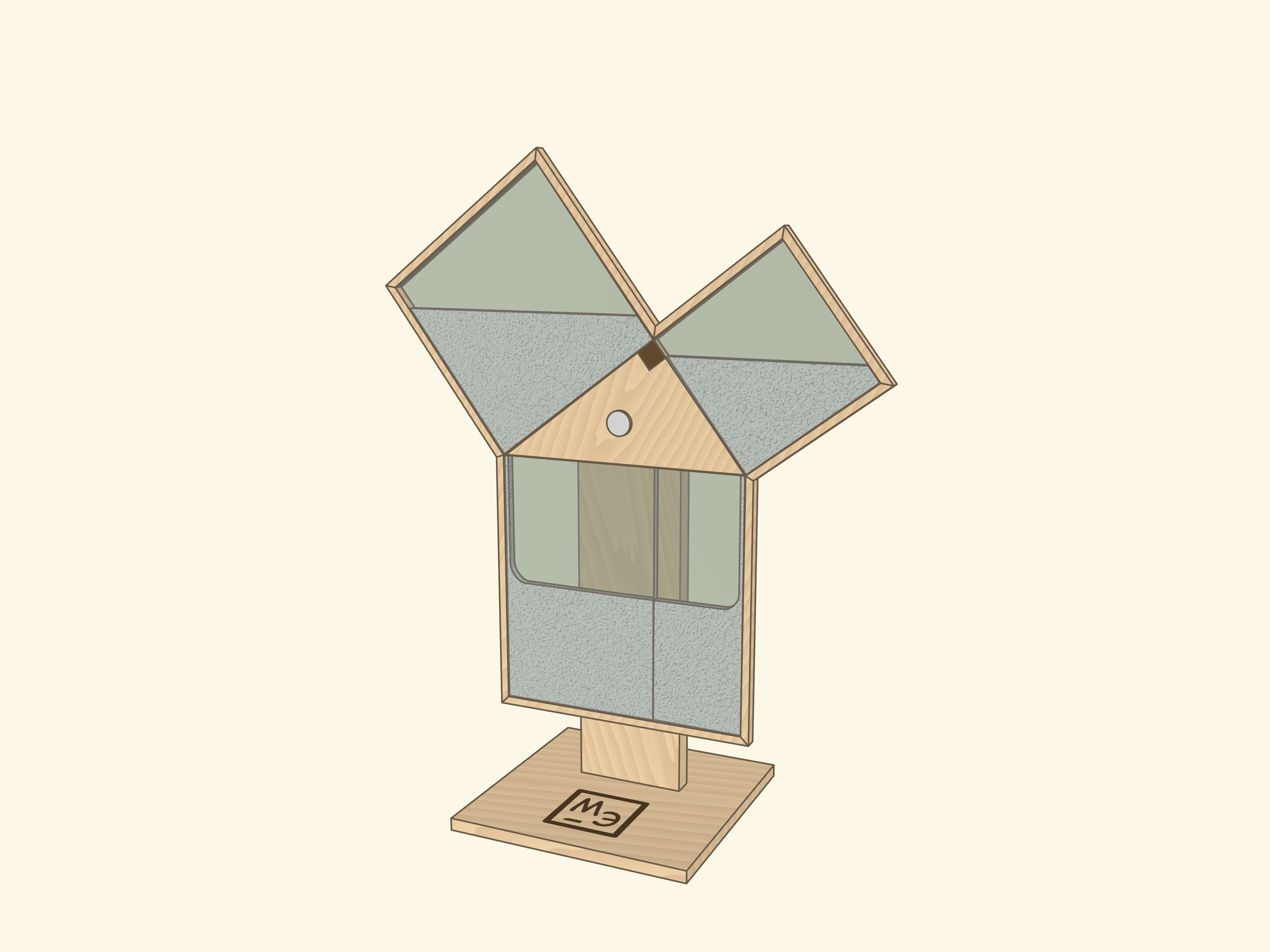
The Pythagorean theorem is probably taught to schoolchildren in all countries and many science museums have an exhibit illustrating it, often with water rather than sand.
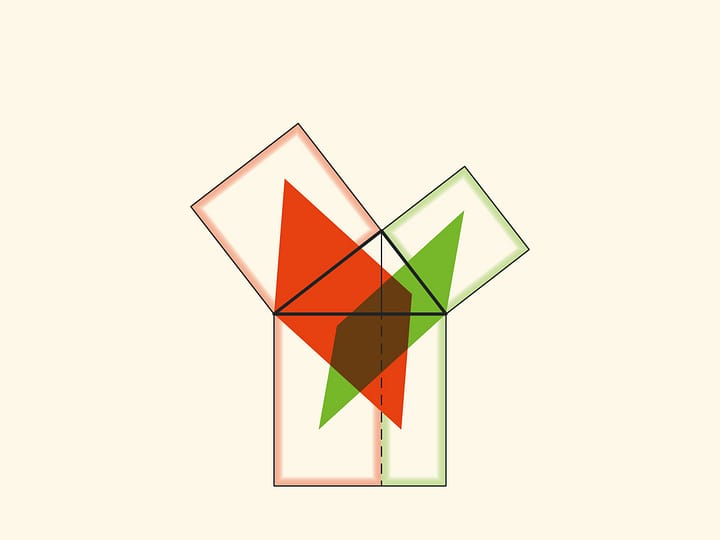
In both cases it is important to make sure that the squares are filled completely — we are talking about equality of areas! Technically and visually, strips between squares with “reserves” of sand or water, closed off from the observer’s view, can help.
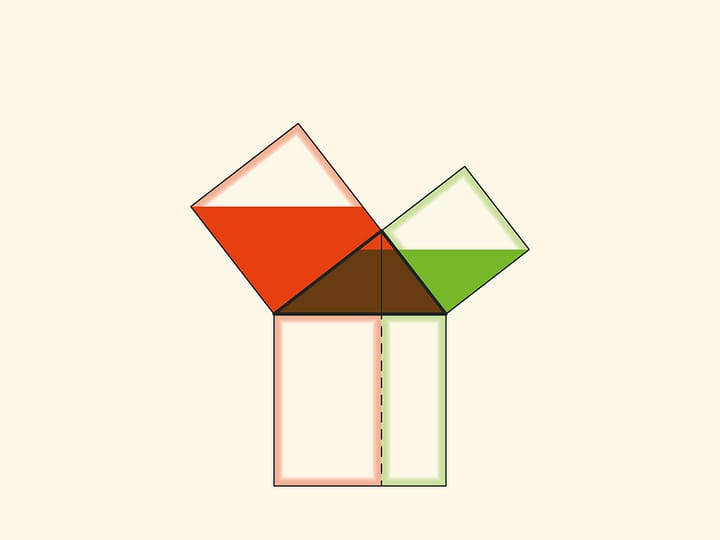
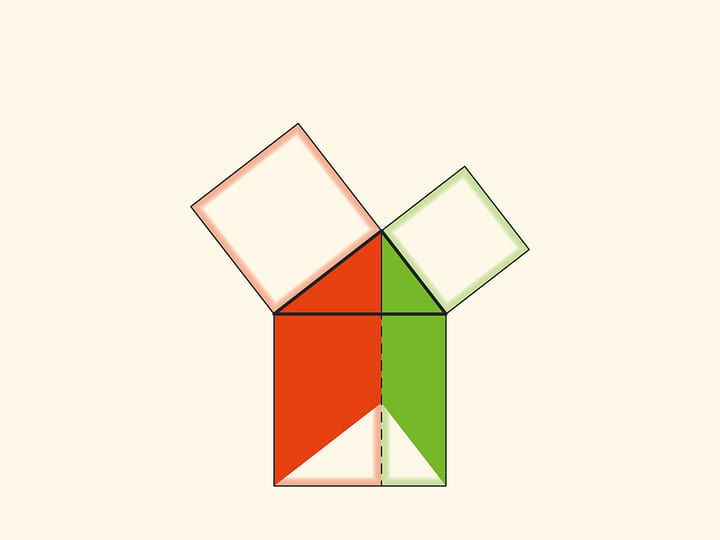
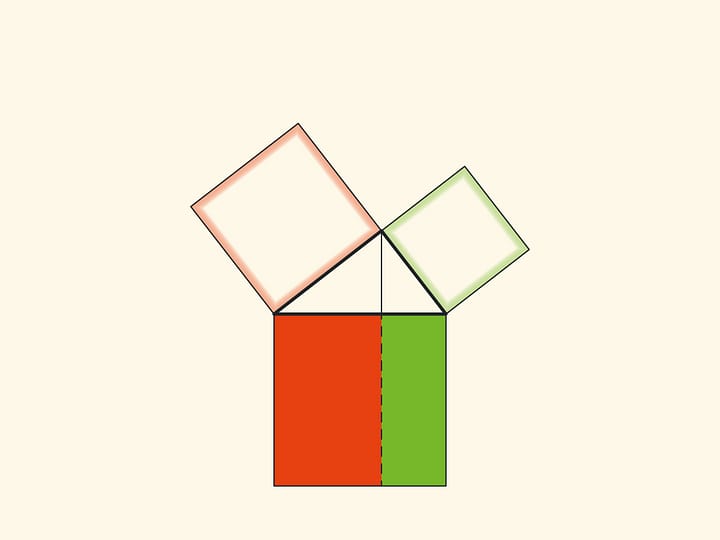
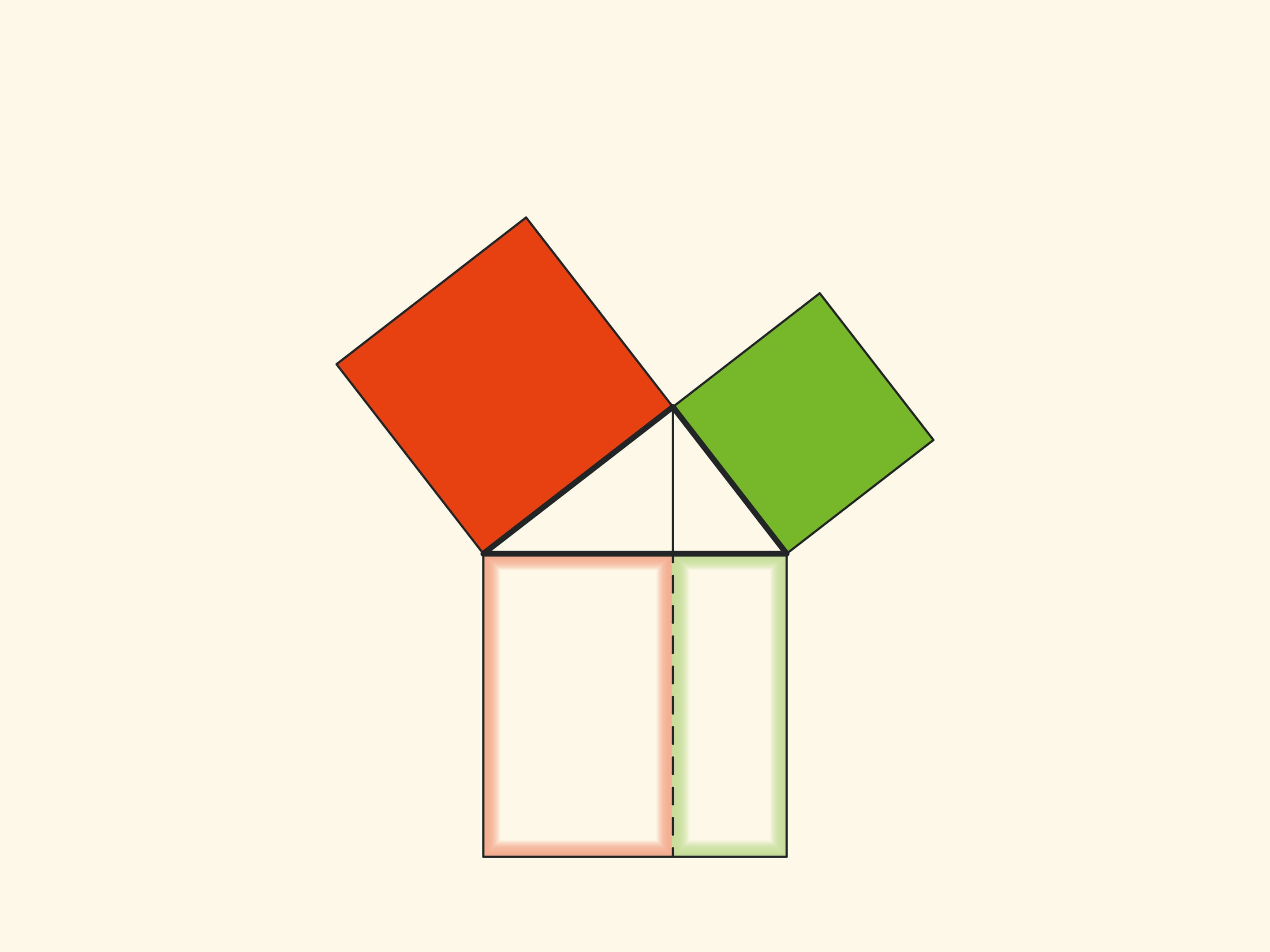
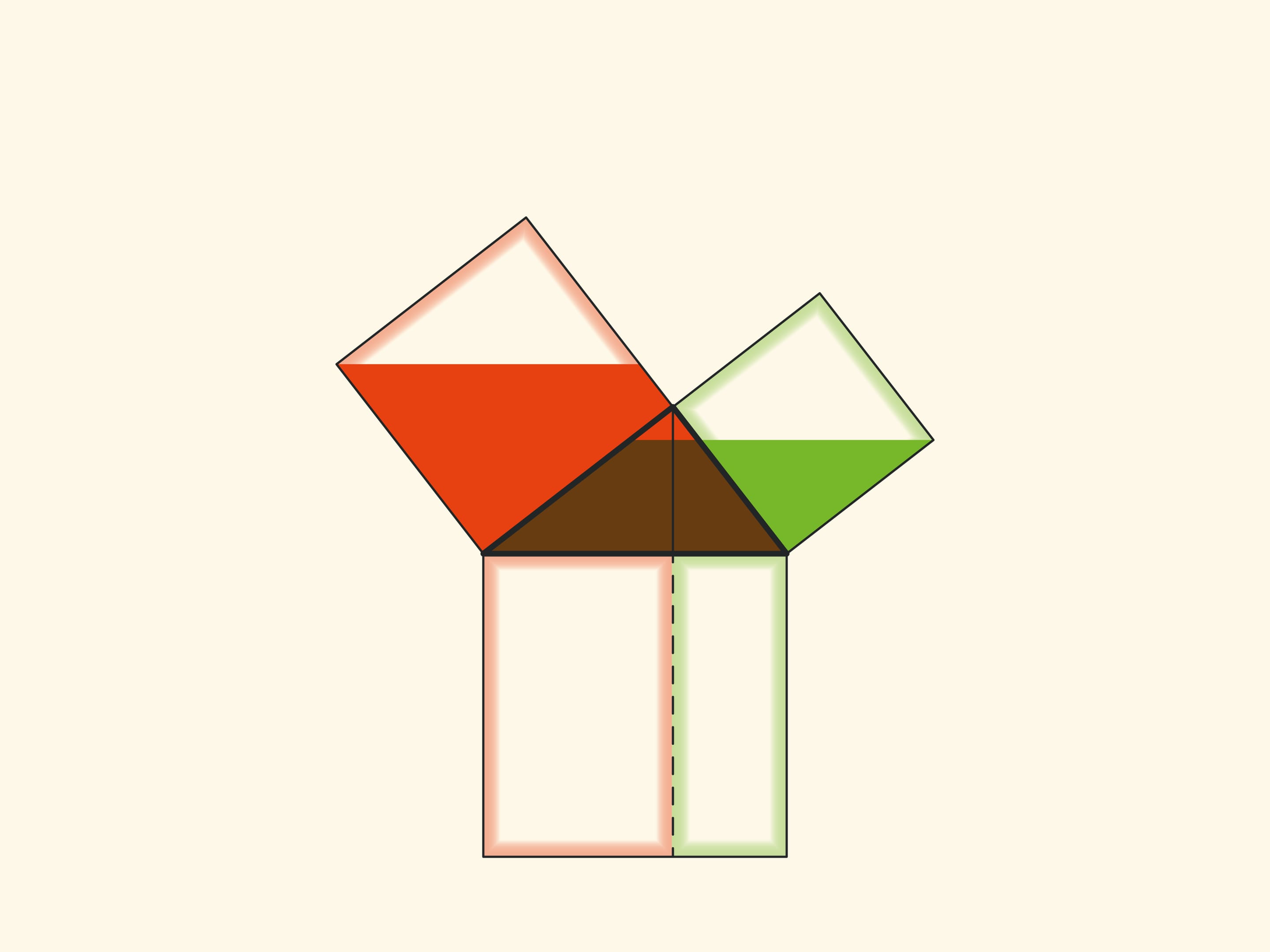
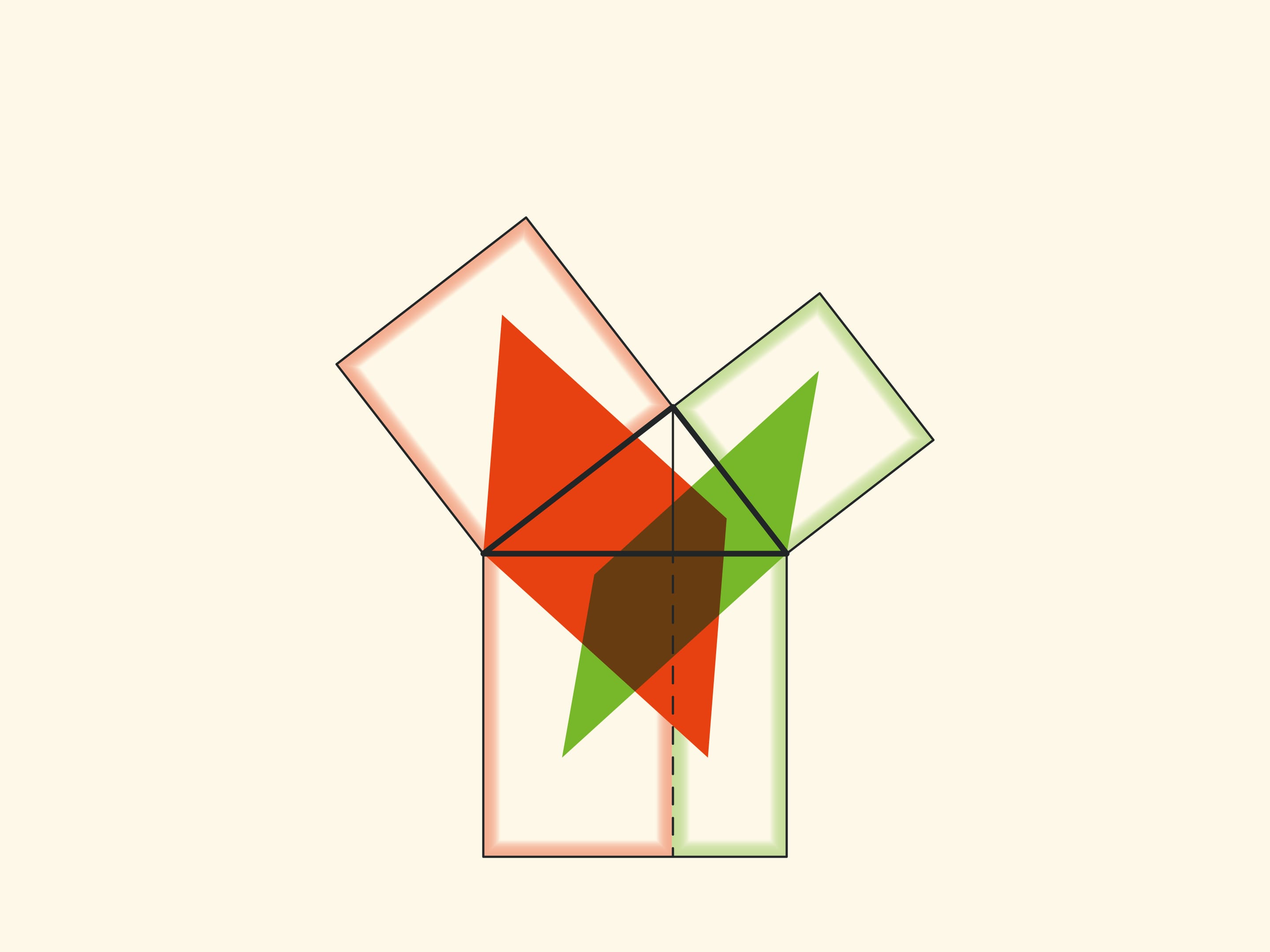
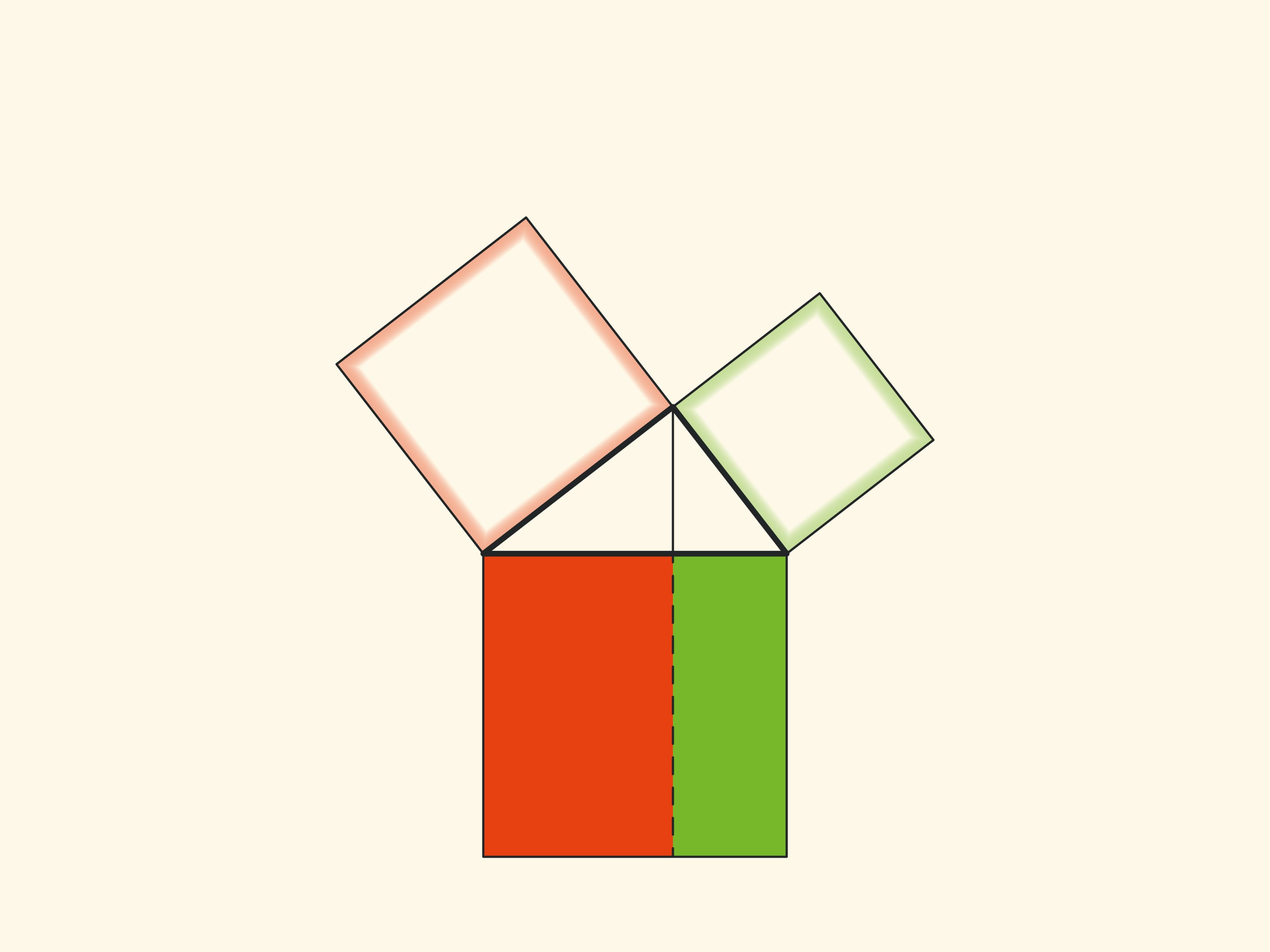
Note another important detail. The square built on the hypotenuse is divided into two parts by the continuation of the altitude of the right triangle, dropped from the top of the right angle. It turns out that the smallest of the resulting rectangles is equal in area to the square built on the smaller cathetus, and the larger is equal to the square built on the larger cathetus.
Technically, this allows you to work with smaller volumes and, therefore, with fewer errors. And most importantly, this observation allows constructing not illustrations, but real proofs of the Pythagorean theorem like “Look!”. And in essence it is similar to the one given in the “Elements”. These beautiful and elementary proofs may be seen here: Pythagorean Theorem: Euclid's proof page.