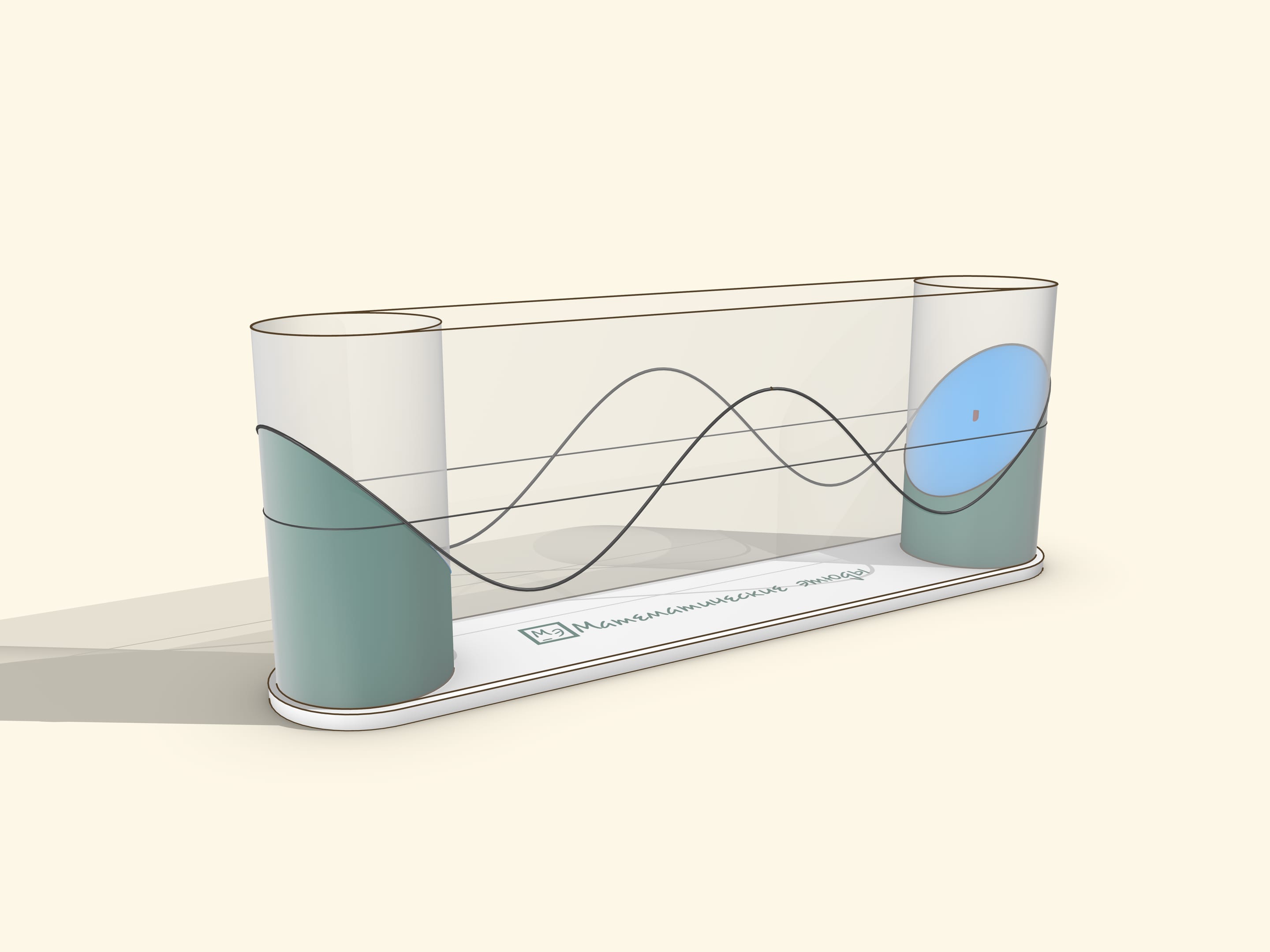
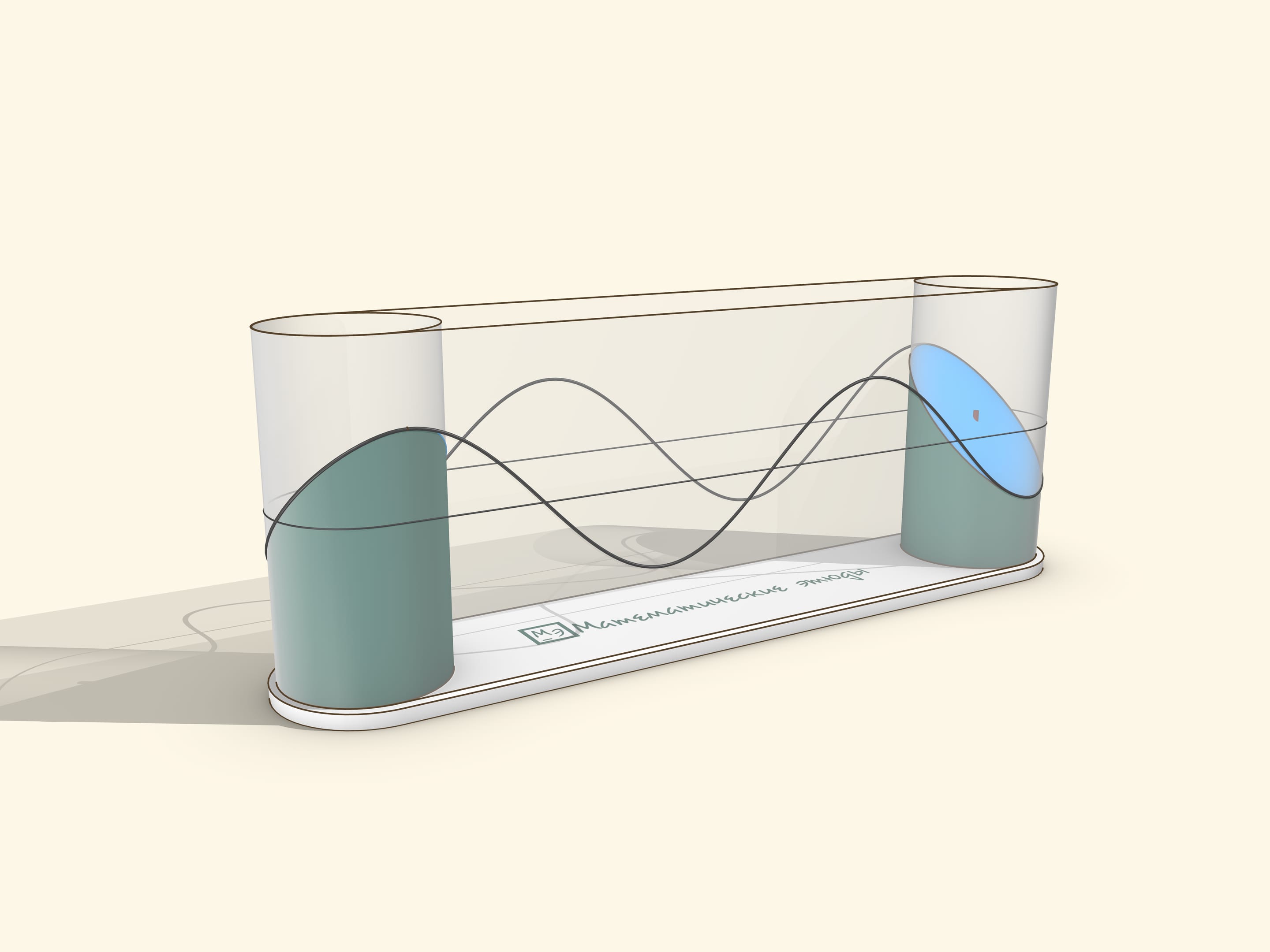
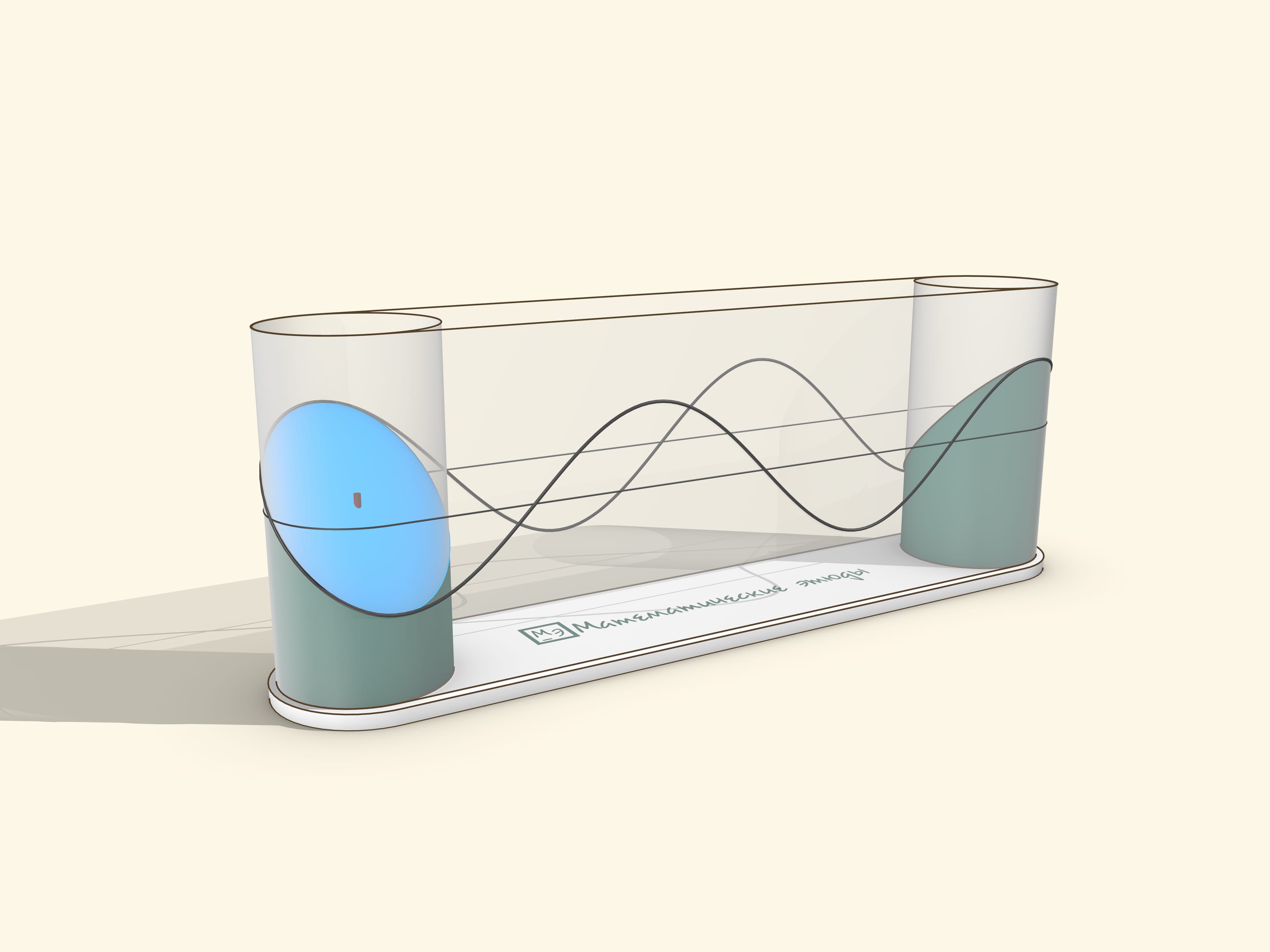
A sine graph can be obtained as a “cut off at an angle” cylinder (or, similarly, with an ellipse drawn on it).
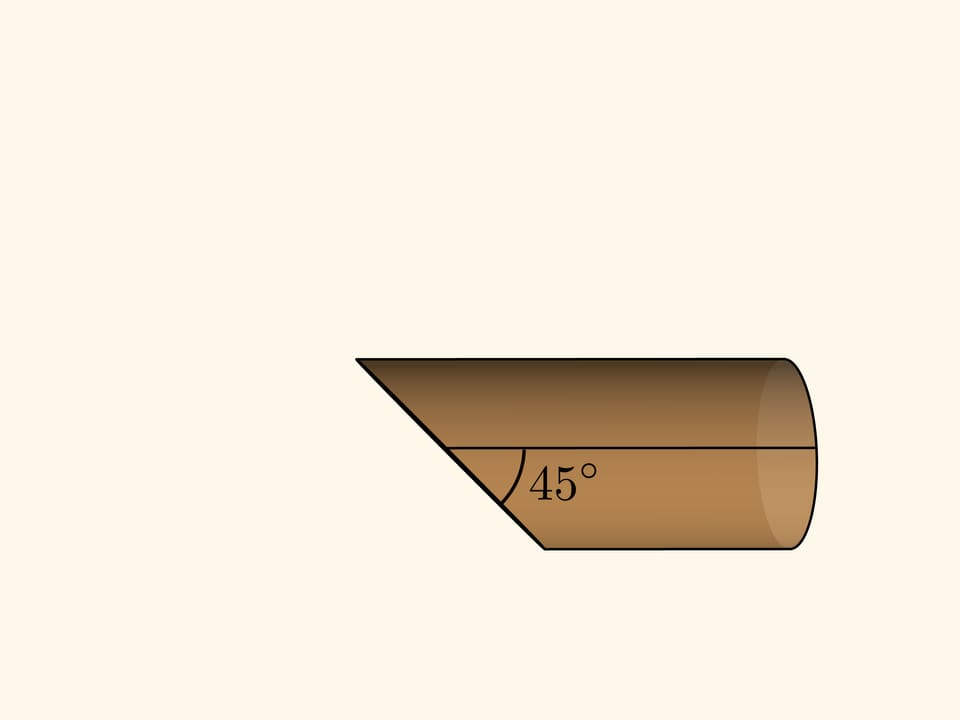
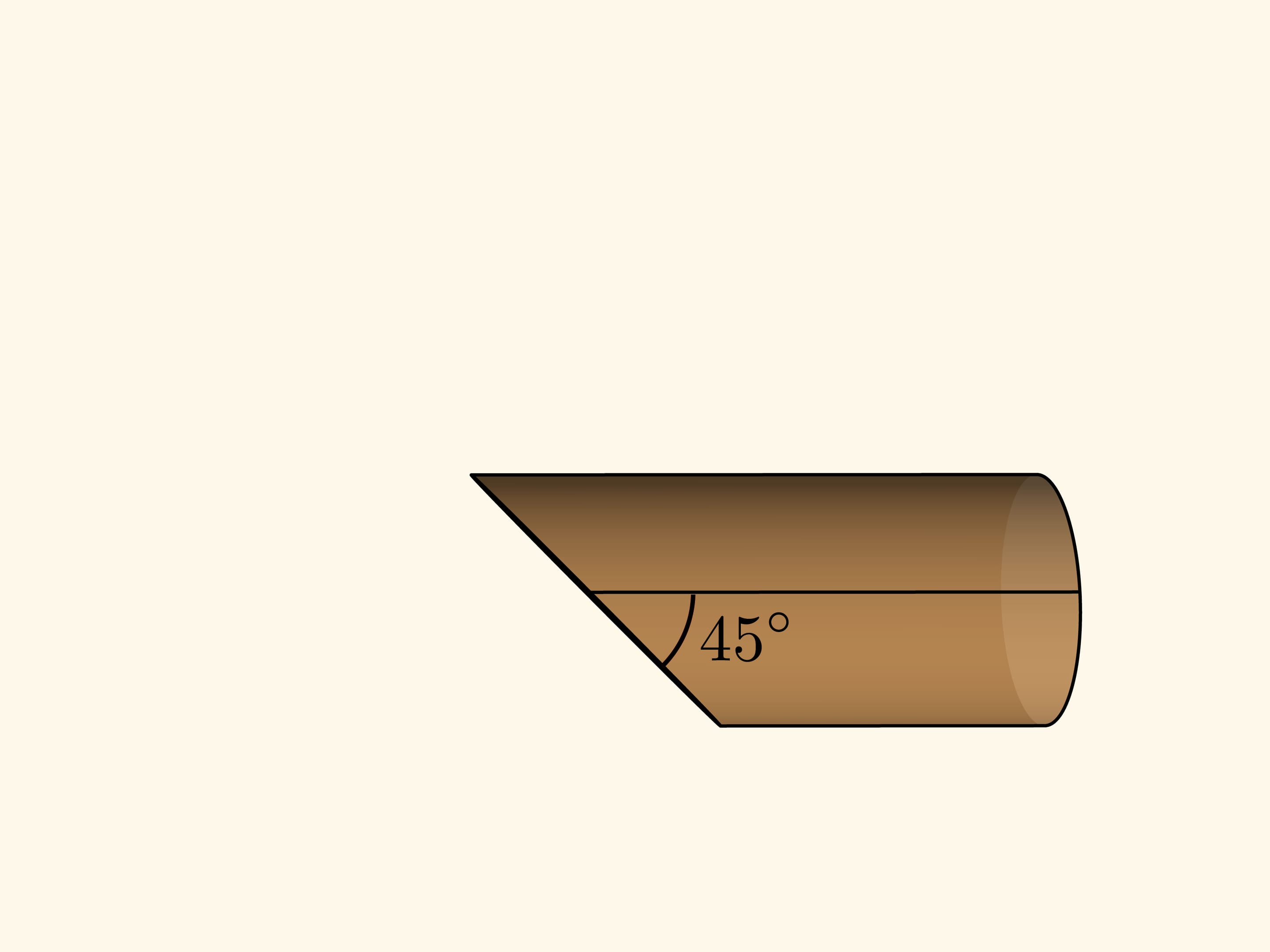
All you need to get a sine wave at home is a loaf of sausage. It is known that sausage must be cut at an angle — then the pieces are bigger.
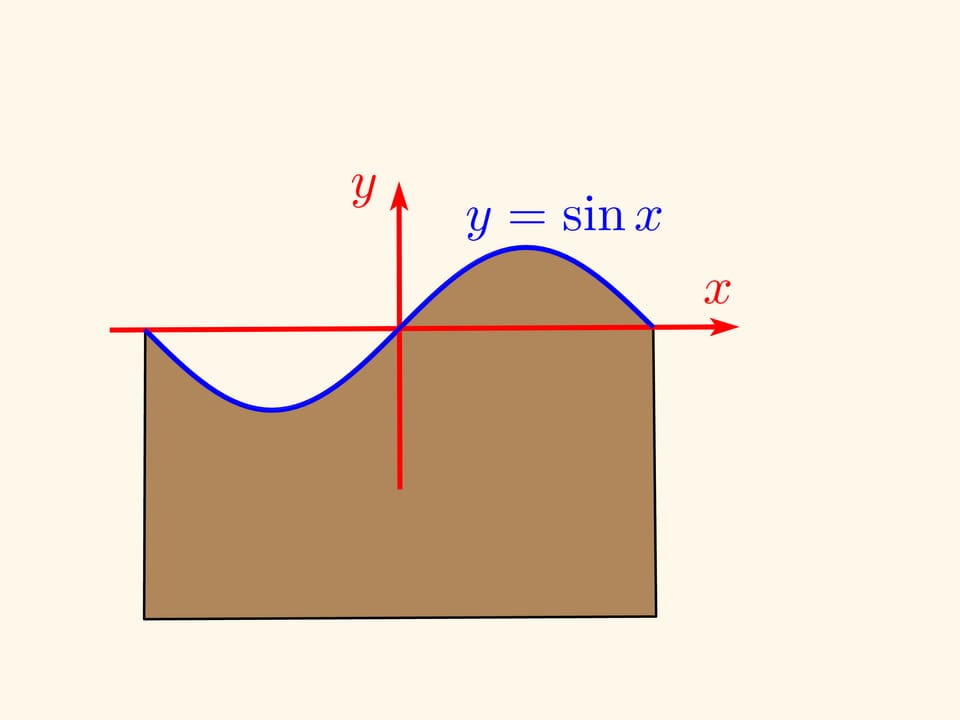
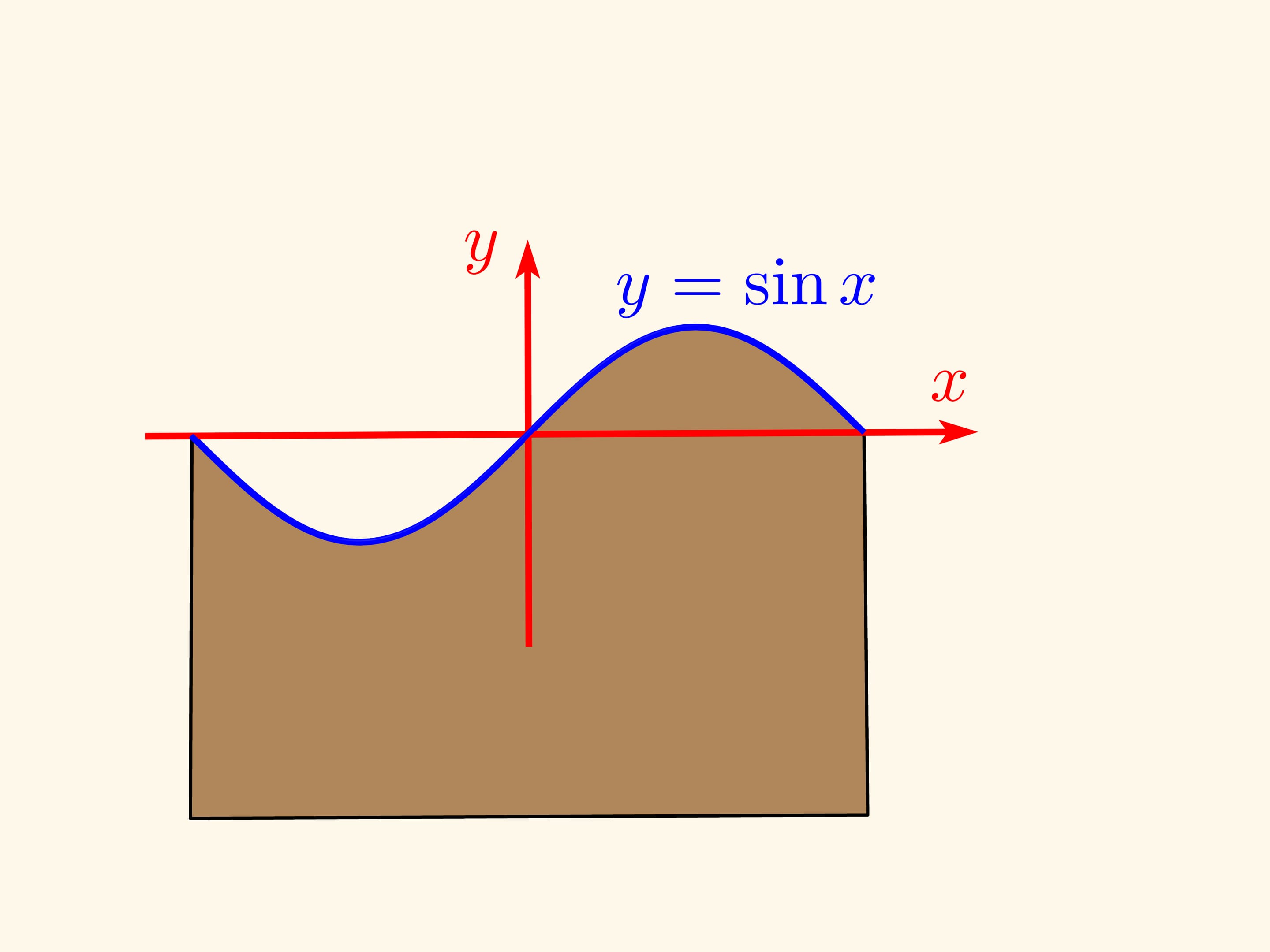
Let’s slice the casing along the still uncut part of the sausage and flatten the casing. If the cutting angle is 45° to the cylinder axis (taking its radius as a unit), then one edge of the casing (the cylinder net) will be exactly a sine wave — the graph of function $y=\sin x$! If the angle was arbitrary, $\alpha ,$ the graph will be $y=\tg\alpha \sin x $.
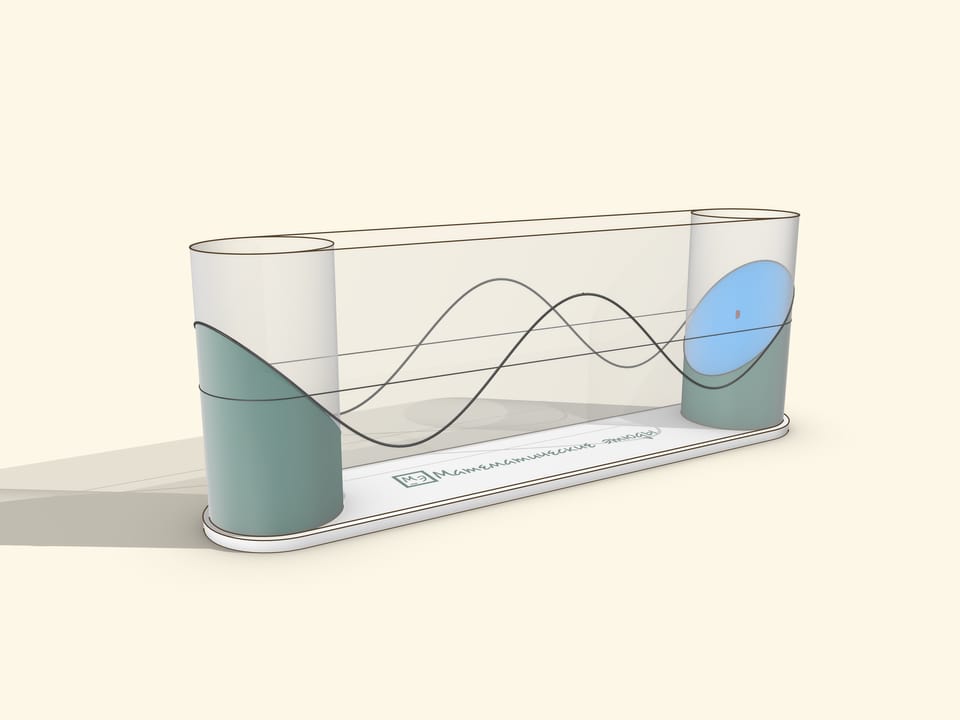
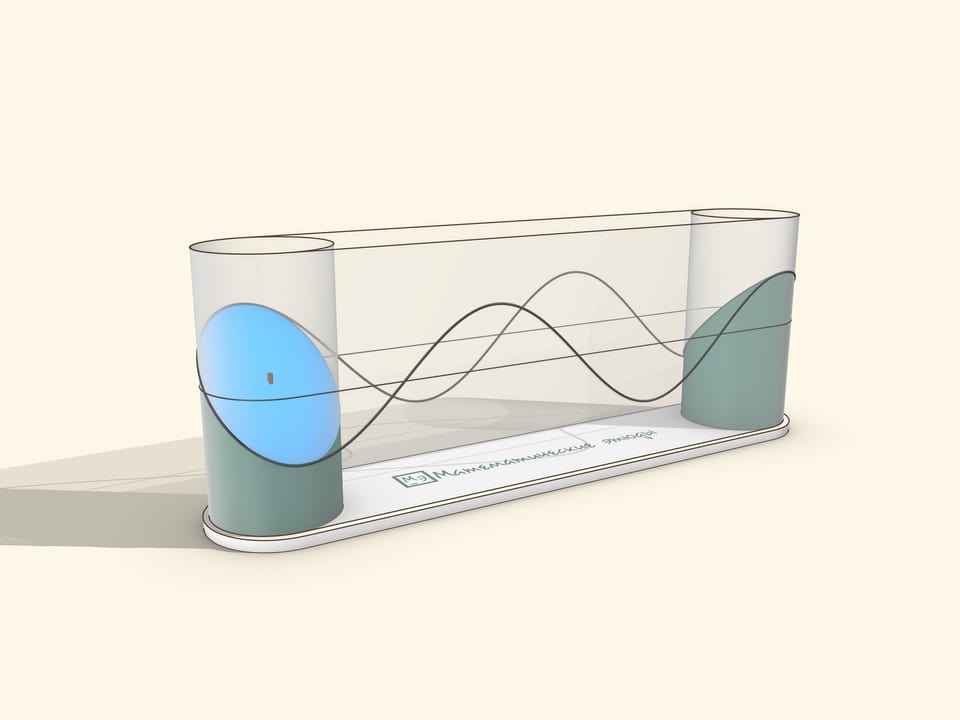
A museum piece can be made by stretching a transparent film over two cylinders. The drive should be manual, so that the user can rotate it at a suitable speed for observation and stop to watch the sine wave roll off the cylinder.
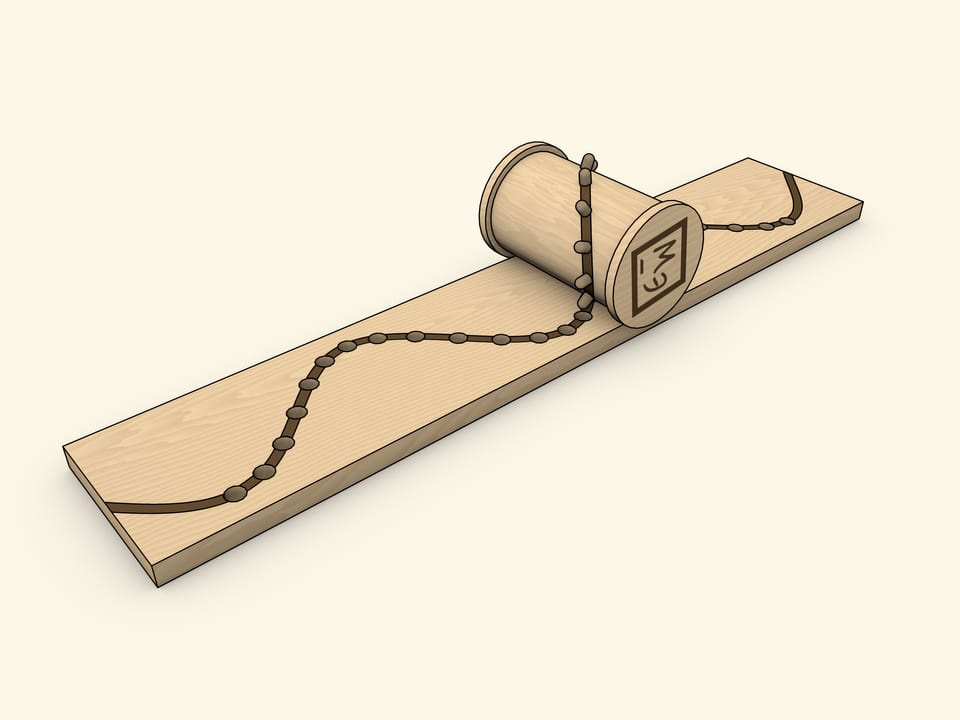
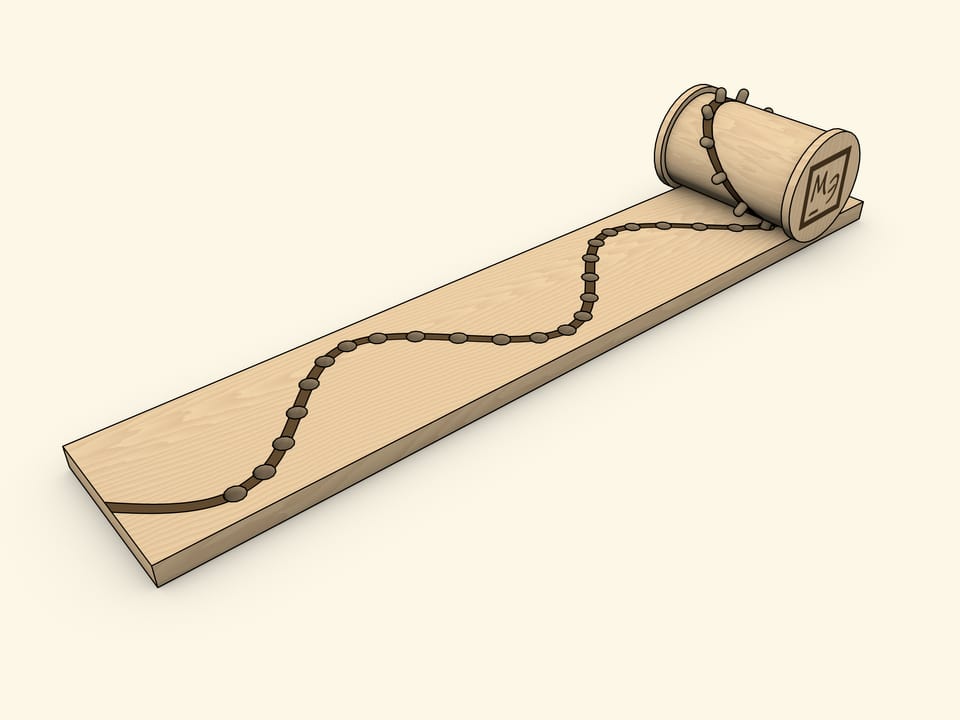
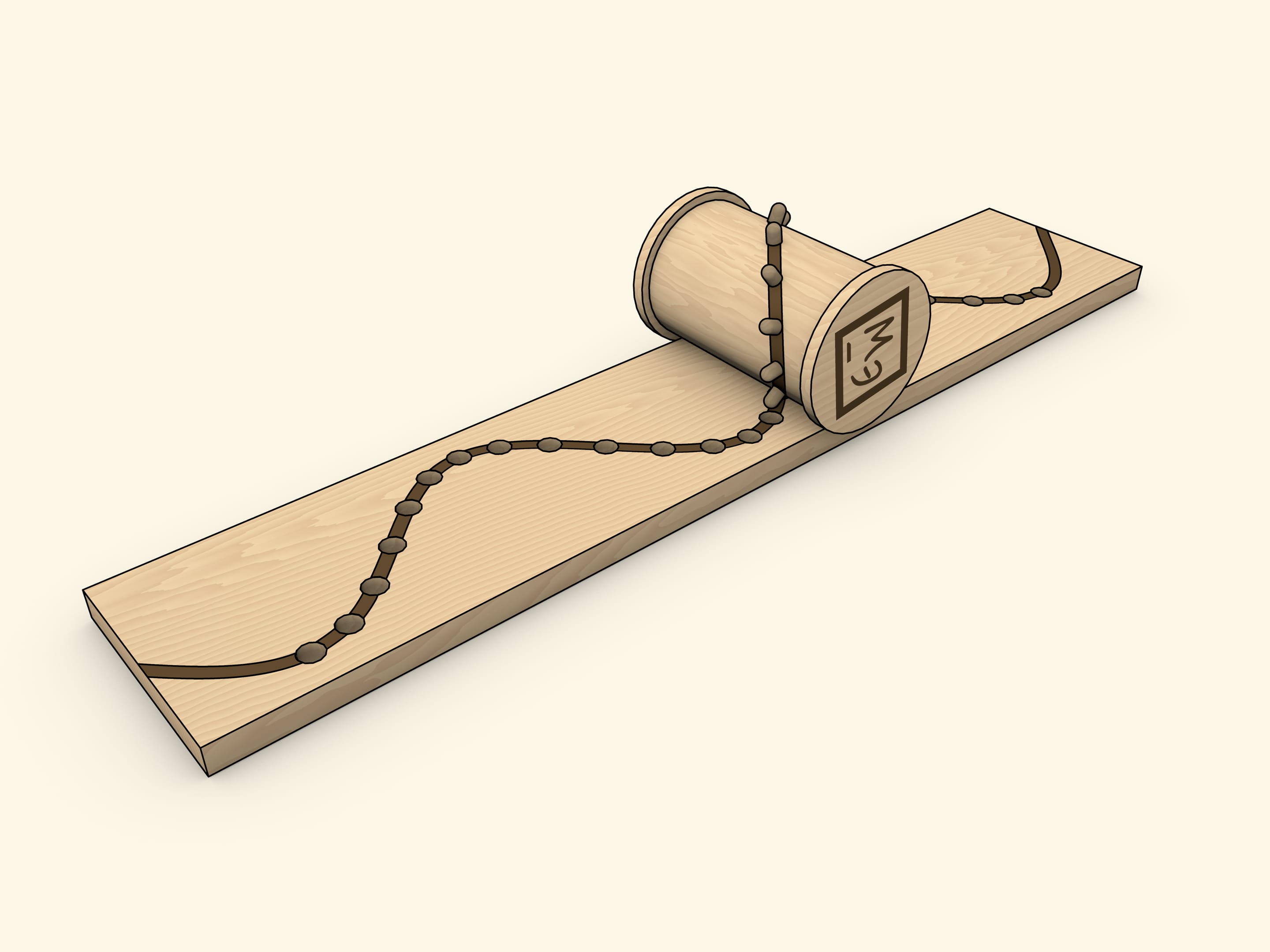
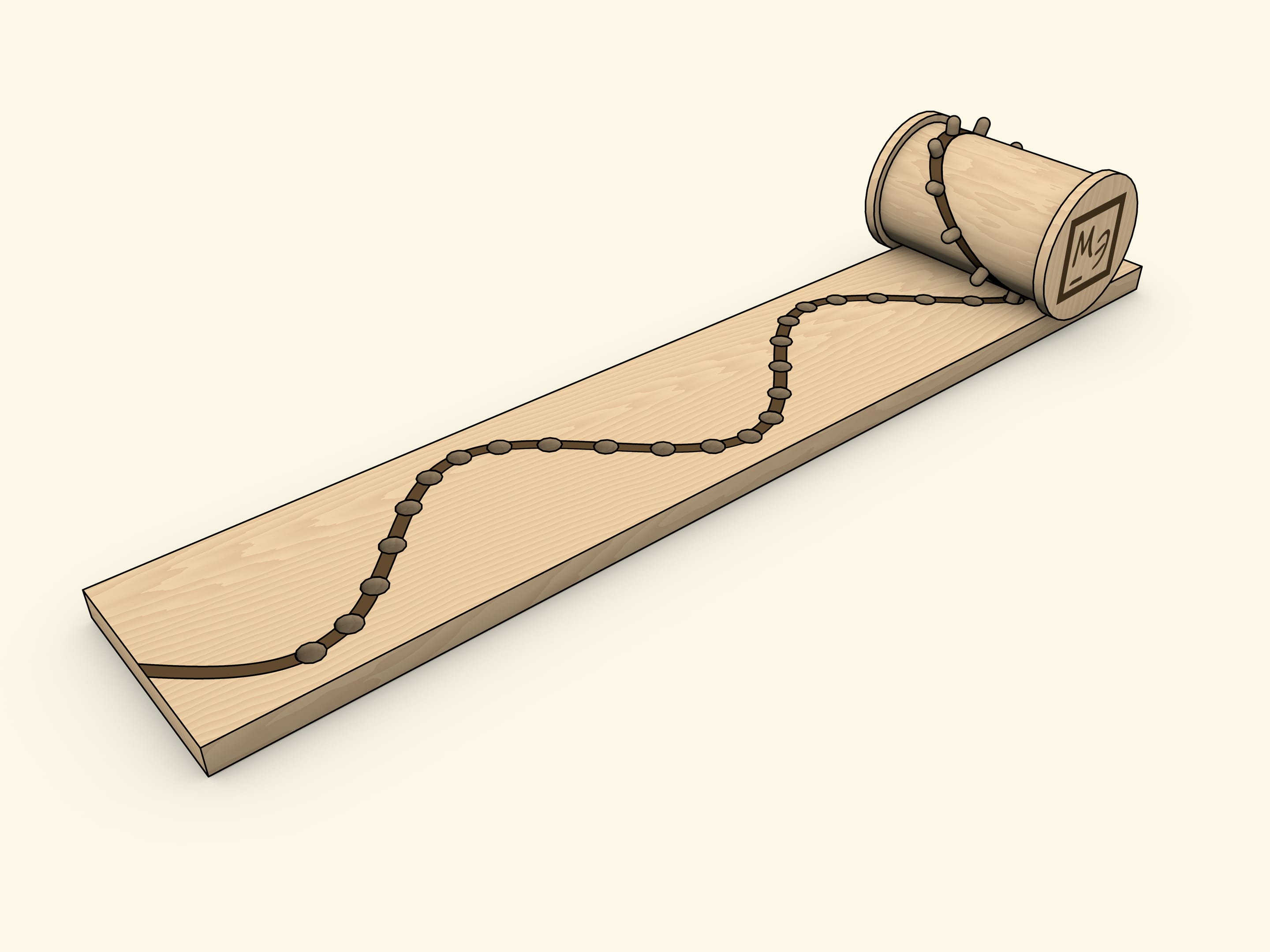
Another “homemade” method of producing a sine wave as a cylinder net is a coil with pins inserted along an ellipse.
The choice of the coil is not accidental: the flange, with a properly adjusted base width, avoids misalignment. With this implementation, the holes in the base need to be cone-shaped and/or wider than the pins, as they must be able to slide in and out “at an angle” unhindered.