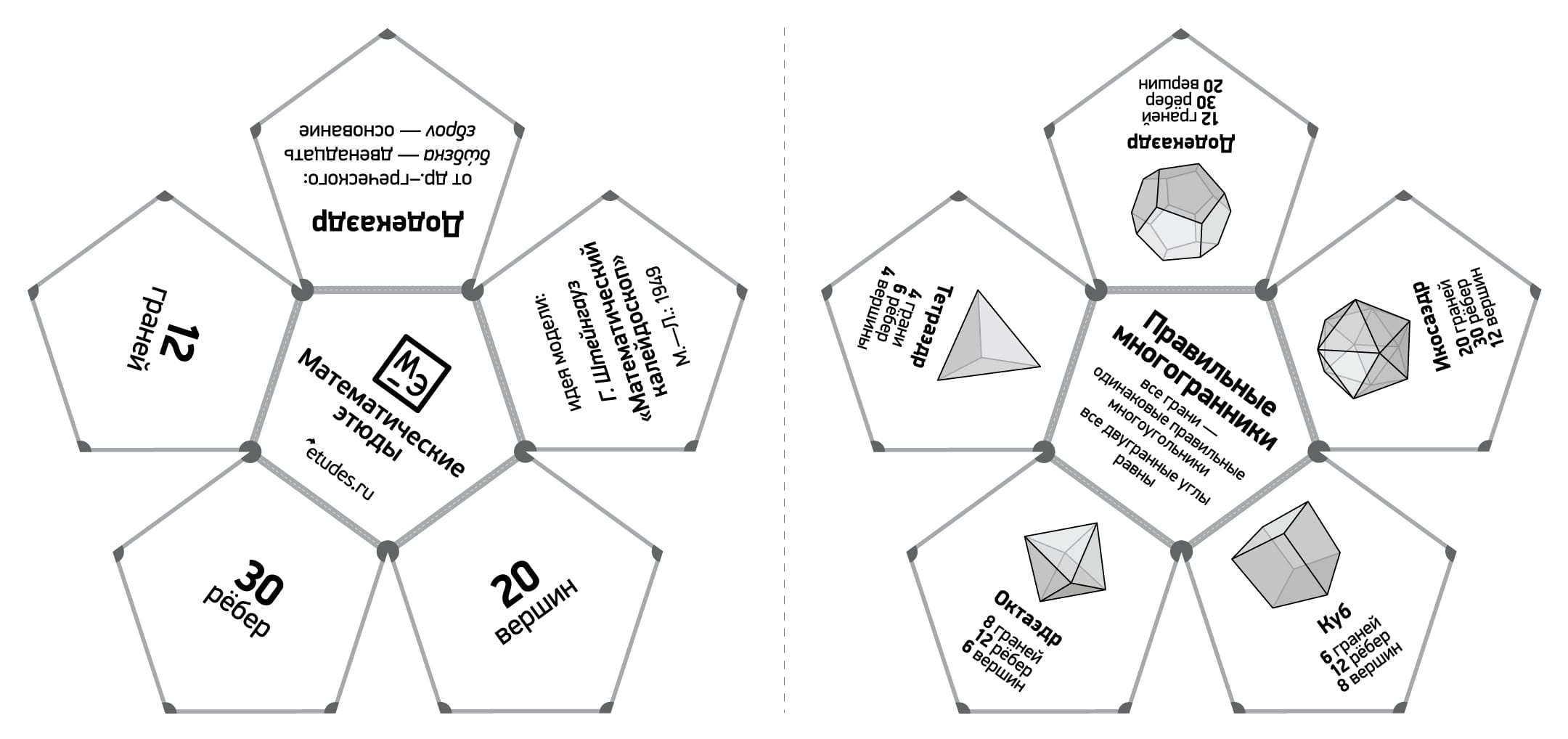
A dodecahedron (from Greek δώδεκα — twelve and εδρον — face) — is one of five regular regular polyhedra. It has 12 faces, which are regular pentagons, 30 edges, 20 vertices.
The idea of a model is proposed in Hugo Steinhaus' book ”Mathematical snapshots” (first edition in Russian: Moscow-Leningrad, 1949).
A model can be manufactured of thick cardboard. Corrugated cardboard, for example, that boxes for office paper are made of, would suffice. A rubber band — like the one a roll of money is binded with — is also needed. In this case the dodecahedron's edge should be around 5 centimeters long.
The layout of the dodecahedron half can be printed on a sheet of regular paper to mark the shape for cutting from cardboard.
If you now release the model, e.g. by tossing it, the rubber band will pull the halves together, turning the flat structure into a regular dodecahedron.
The final stable position of the rubber band is the shortest path (geodesic) on the dodecahedron. This position is characterized by the fact that for any pair of adjacent edges the angles between the rubber band and the edge are equal, and it does not ”want” to shift relatively to the edge.
Other models in “Polyhedra”
