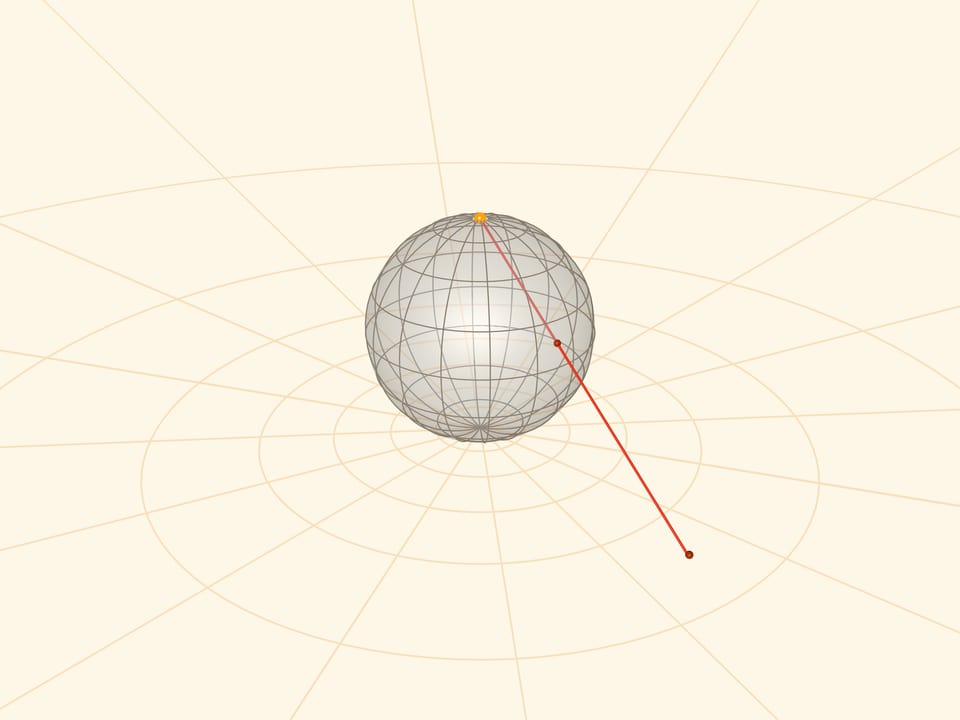
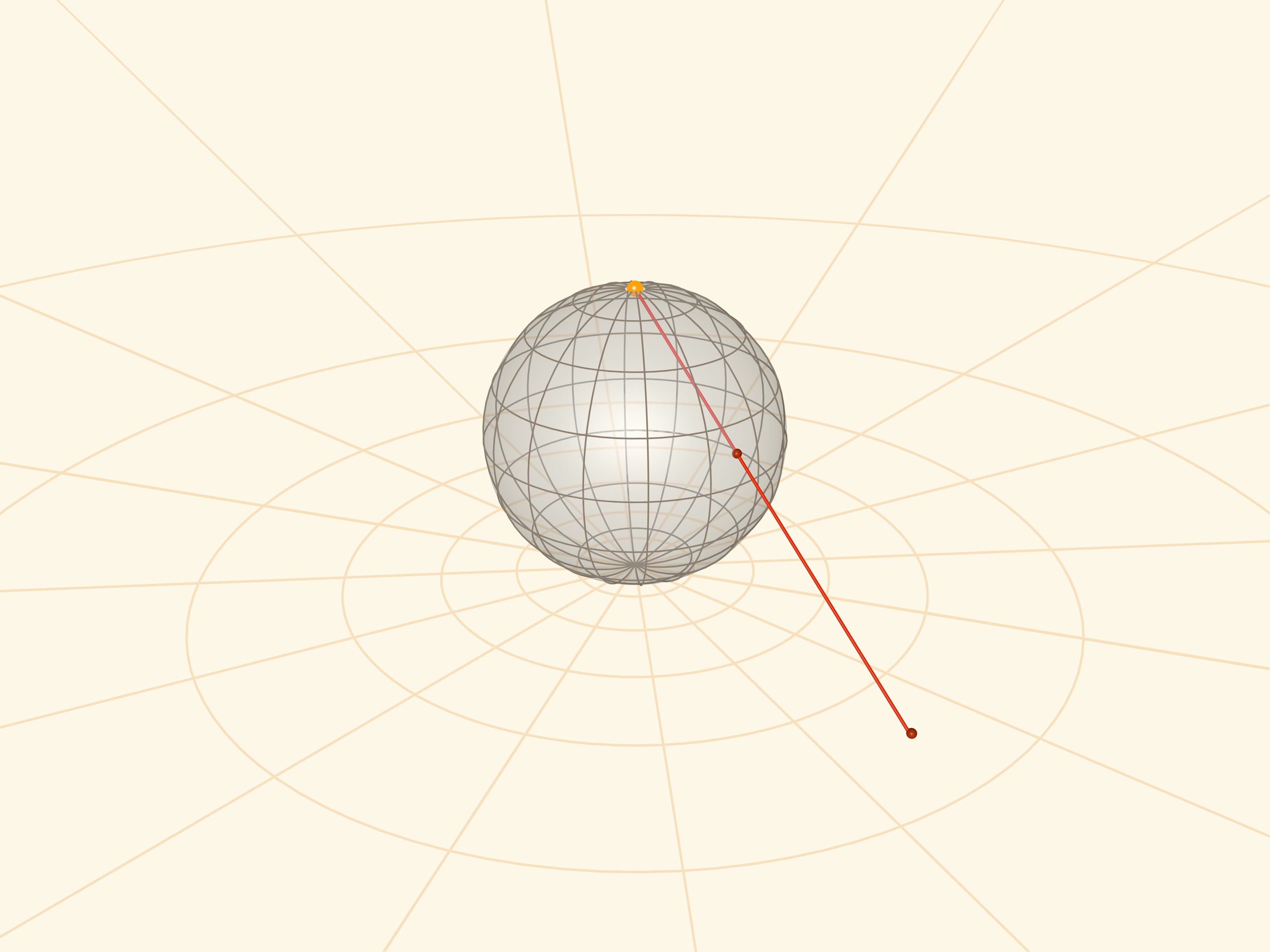
Stereographic projection is the mapping of a sphere (with a pole punctured) onto a plane by the following law. For a point on the sphere, its image on the plane lies on the ray connecting the pole of the sphere — the centre of the projection — with the point on the sphere. This mapping is mutually unique and “works” in both directions.
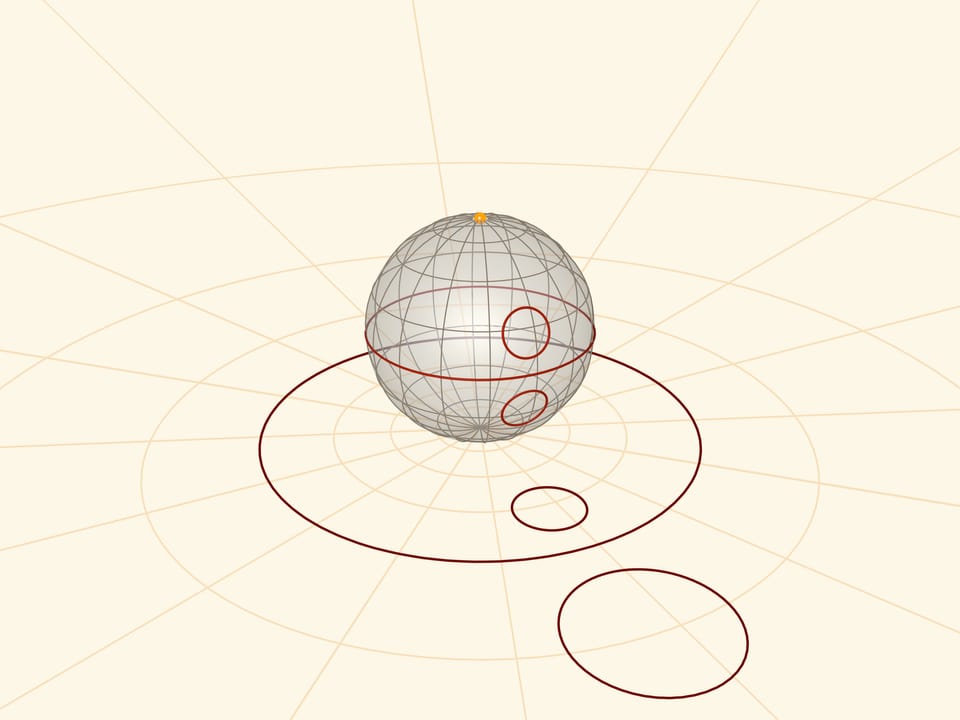
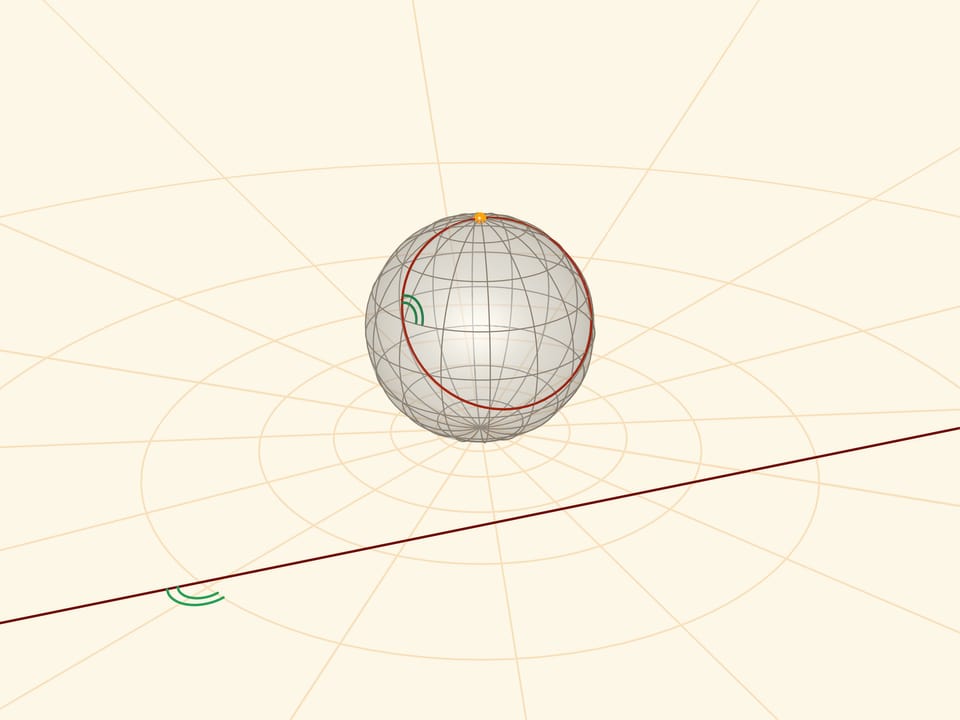
Stereographic projection preserves angles between lines, and translates any circles on the sphere into circles on the plane. More precisely: circles not passing through the projection centre turn into circles in the plane and those passing through it (not just meridians!) turn into straight lines.
Another property: the curves symmetric on the sphere with respect to the equator turn inversely to each other on the plane with respect to the equator projection.
One can realize a stereographic projection by placing a small (point) light source at the pole of the sphere.
A beautiful model: stripes on the sphere which are the (pro)image of a square grid on the plane. It can be made by sticking the stripes on a transparent sphere or, even better, by printing the model on a 3D-printer.