Trapezoid area ⁠

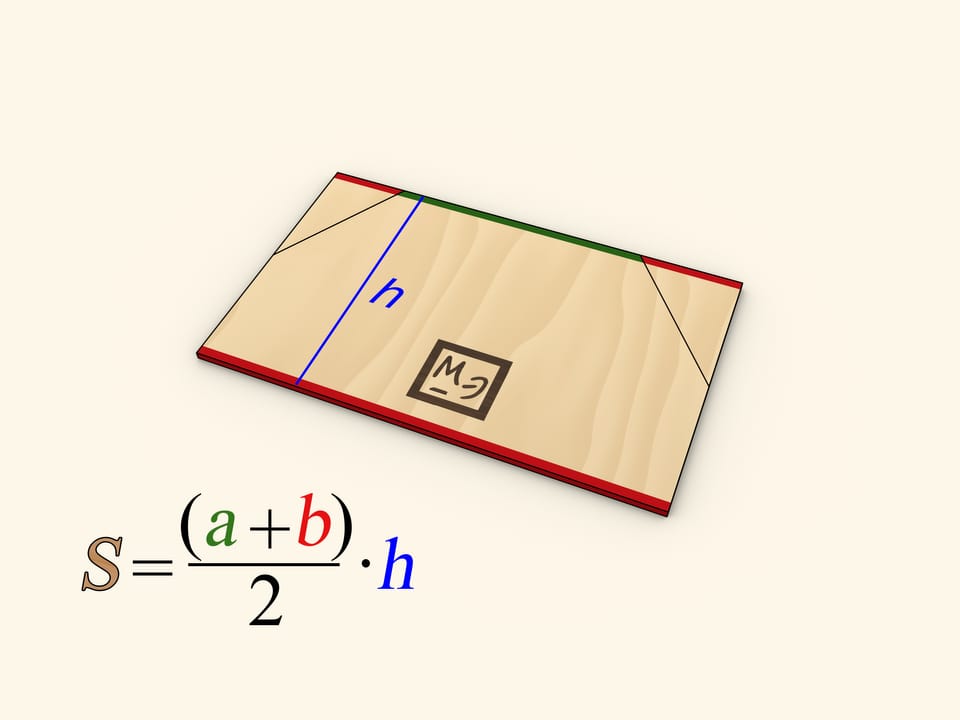
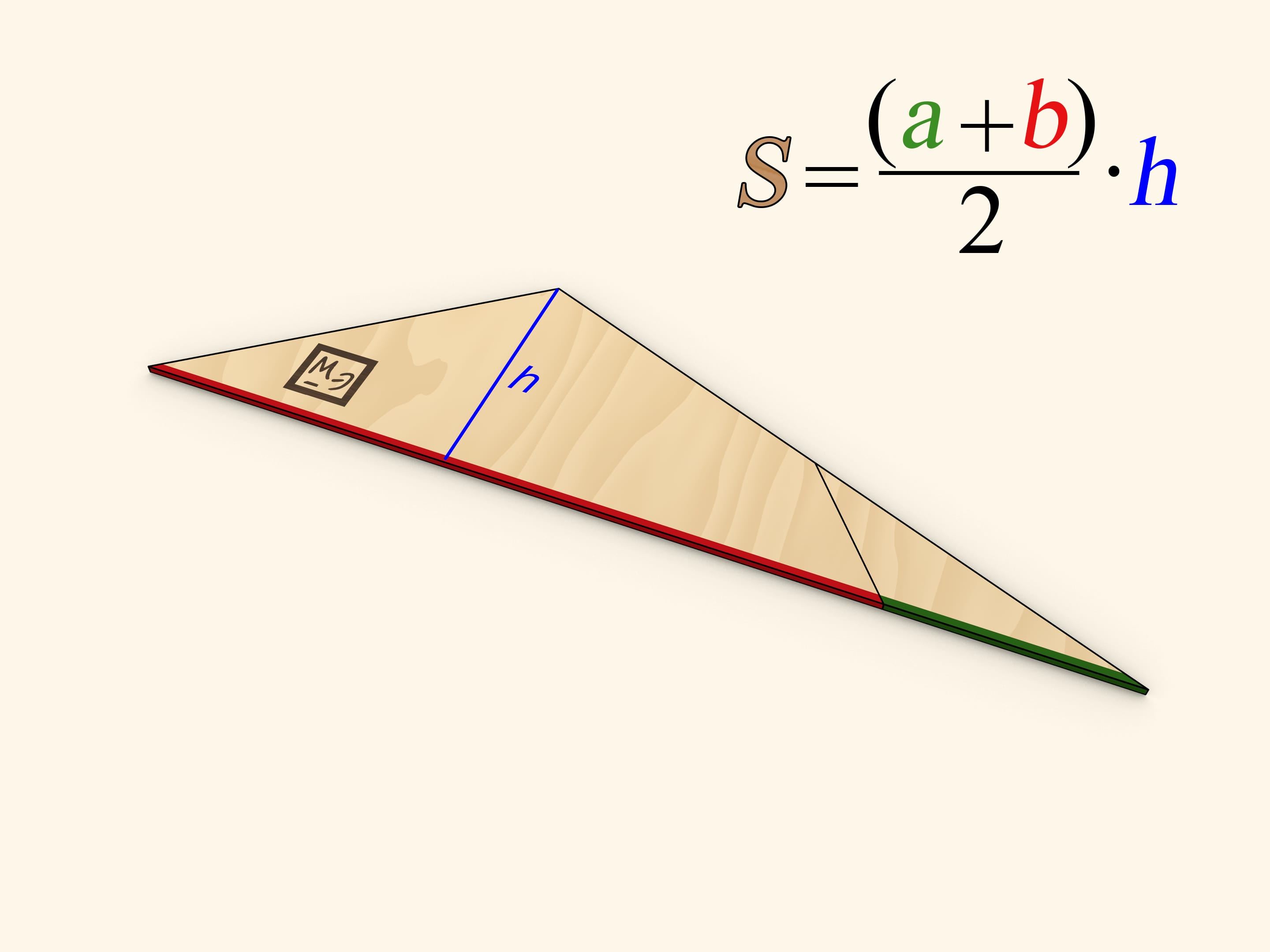
Area of a trape­zoid with bases of lengths $a$ and $b$ and of height $h$ equals $S=(a+b)/2 \cdot h$. One can make sure of that using the formula for the area of a triangle. To achieve it, the trape­zoid should be cut into several pieces that can be rearranged to form a triangle or rectangle.

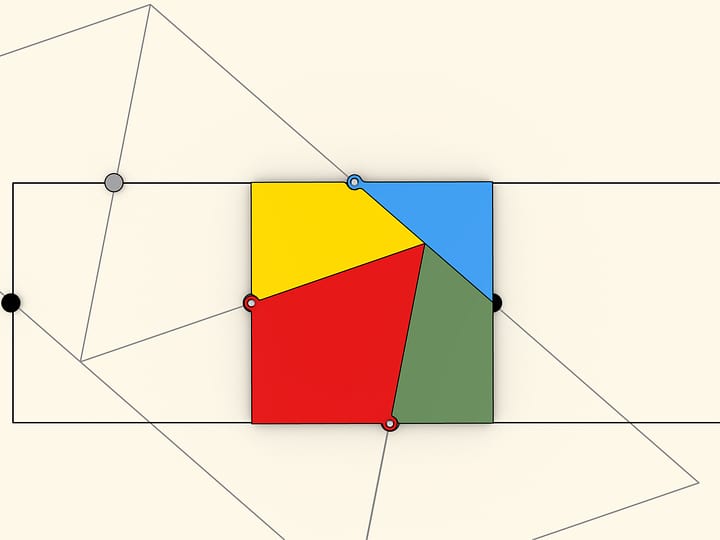
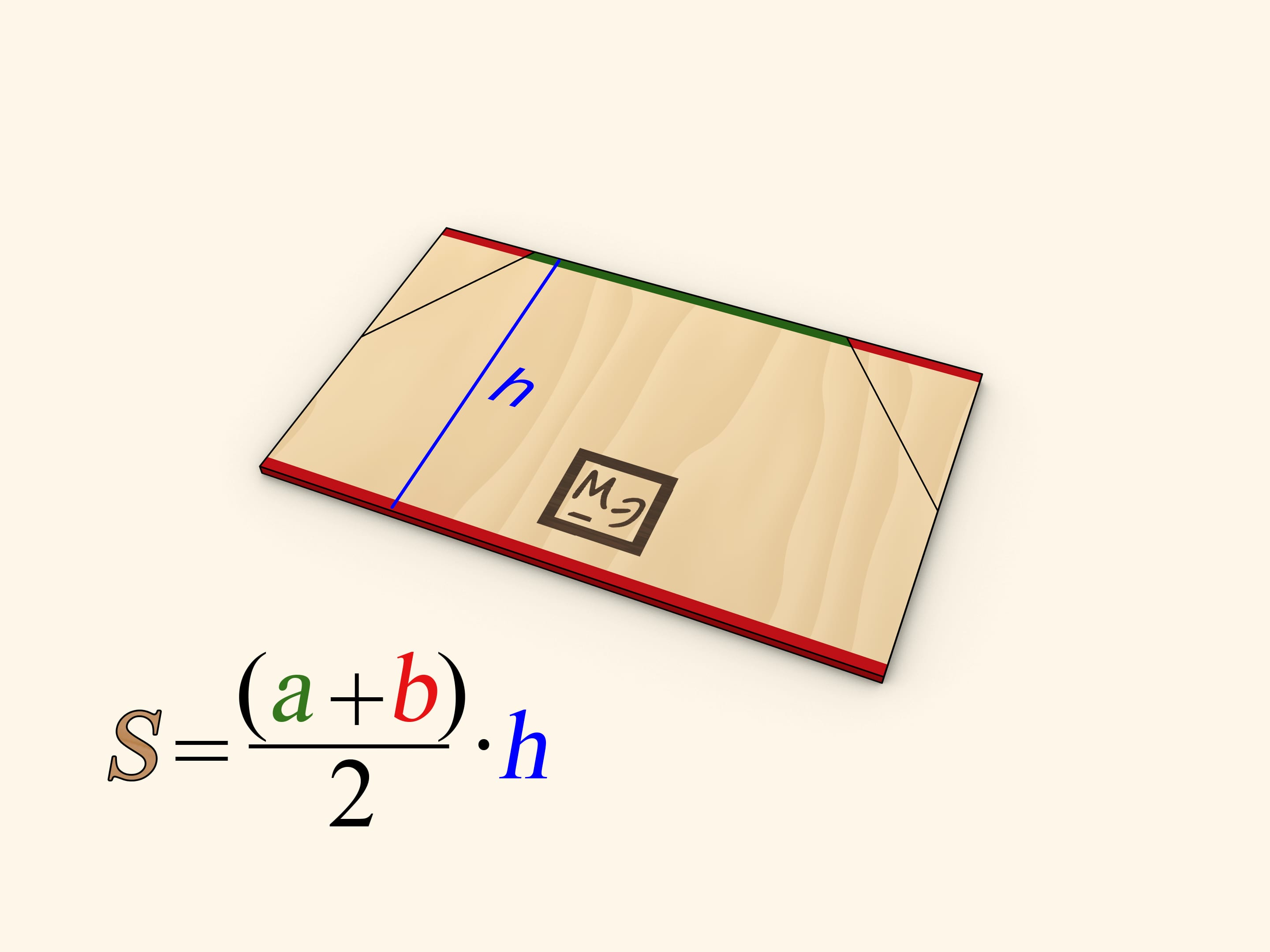
This formula can be illus­trated using the formula for the area of a rectangle. Drop the alti­tudes to the longer base at the midpoints of trape­zoid's legs and then cut the trape­zoid along the alti­tudes. Attach the two cut off right trian­gles's hypothenuses to the remaining parts of the legs. The shape obtained is a rectangle.

One of the rectangle's sides is as long as $h$ — the trape­zoid's height. Sum of two other sides' lengths equals sum of the trape­zoid's bases' lengths, thus one side is as long as half of that sum, that is $(a+b)/2$. So the triangle's area, and so the area of the initial trape­zoid, equals $ S = (a+b) / 2 \cdot h$.

To prove that completely one still should make sure that the shape obtained after rear­ranging the trian­gles is indeed a rectangle — each short side and each composed long side is a line segment, and the corre­sponding lines are parallel. The fact that the angles obtained are right is provided by the cutting method itself — cuts are made along the alti­tude perpen­dic­ular to the base.

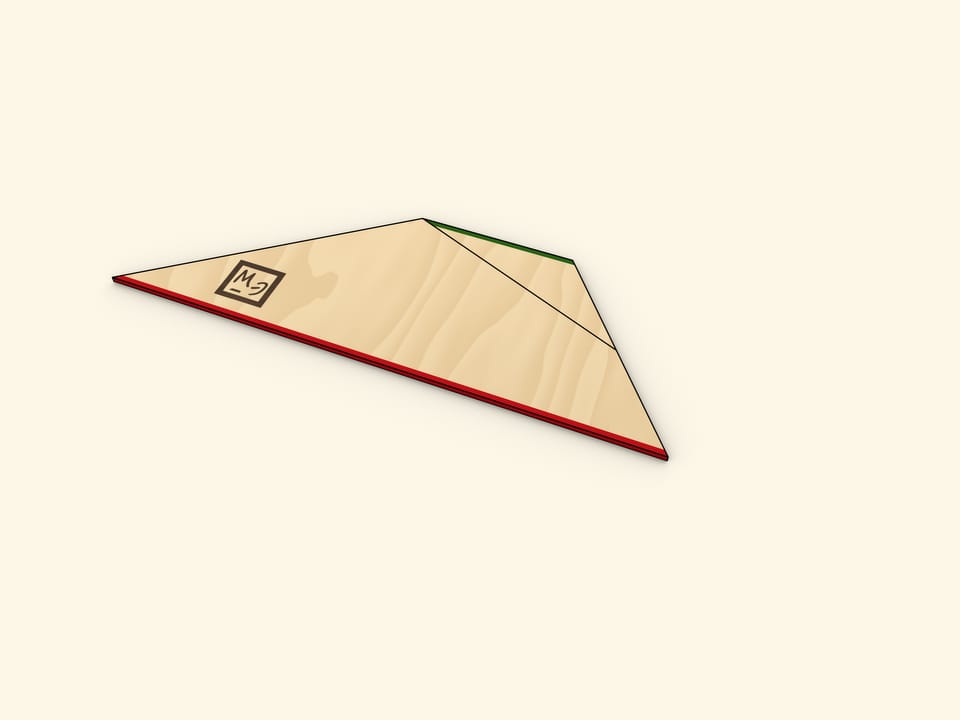
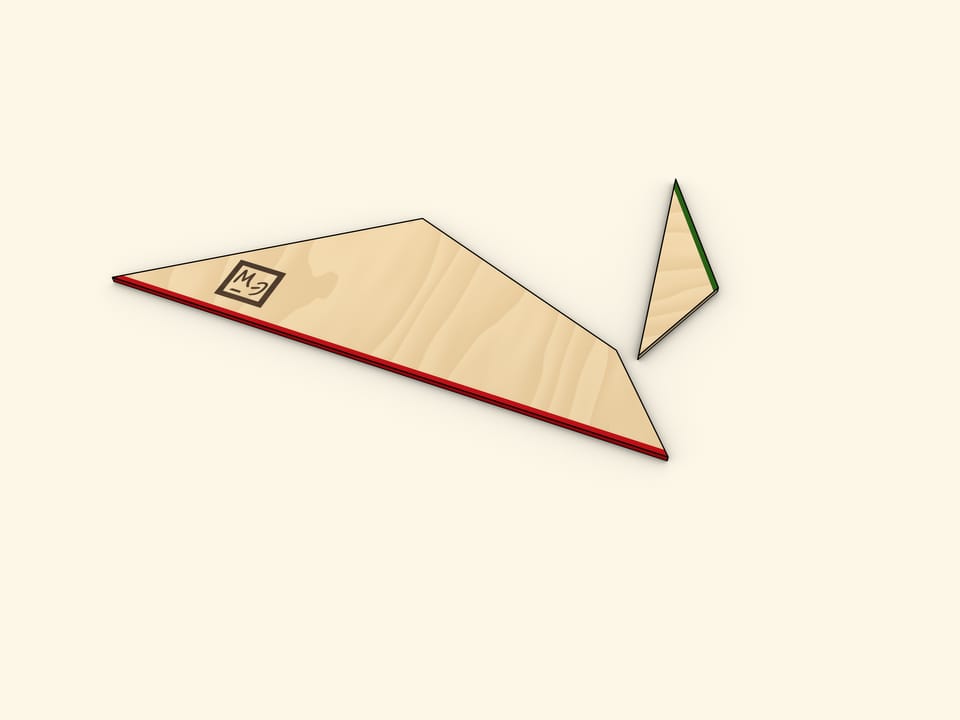
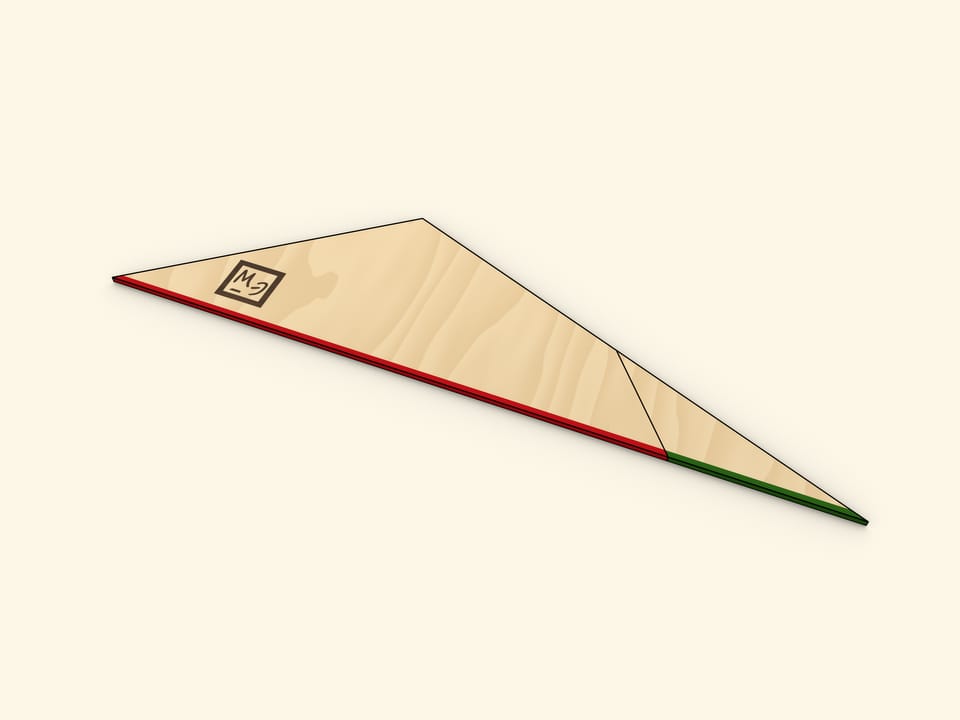
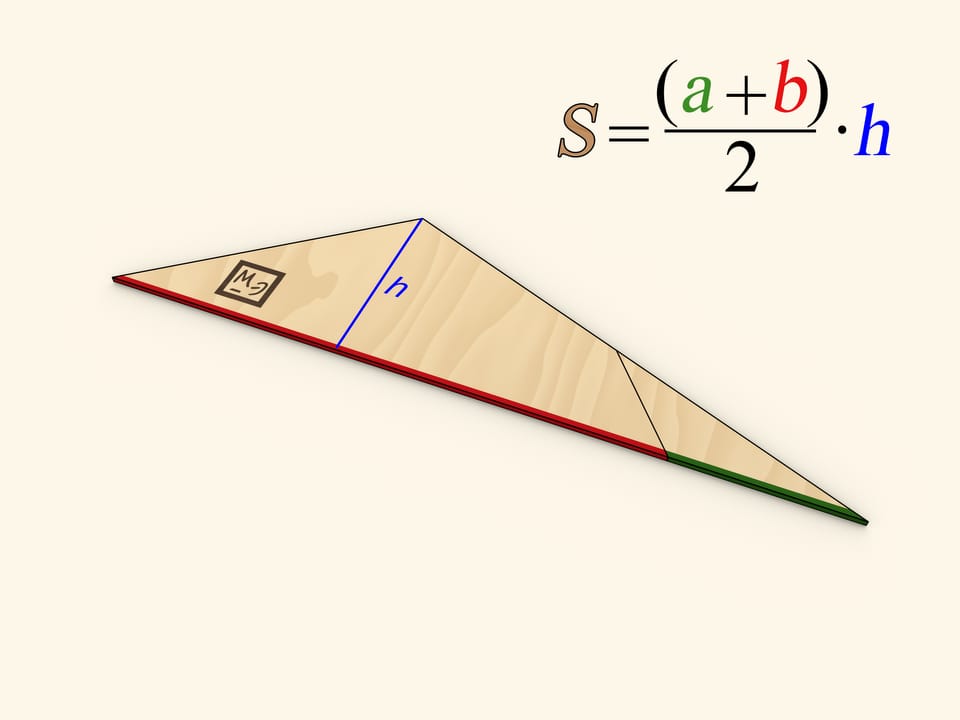
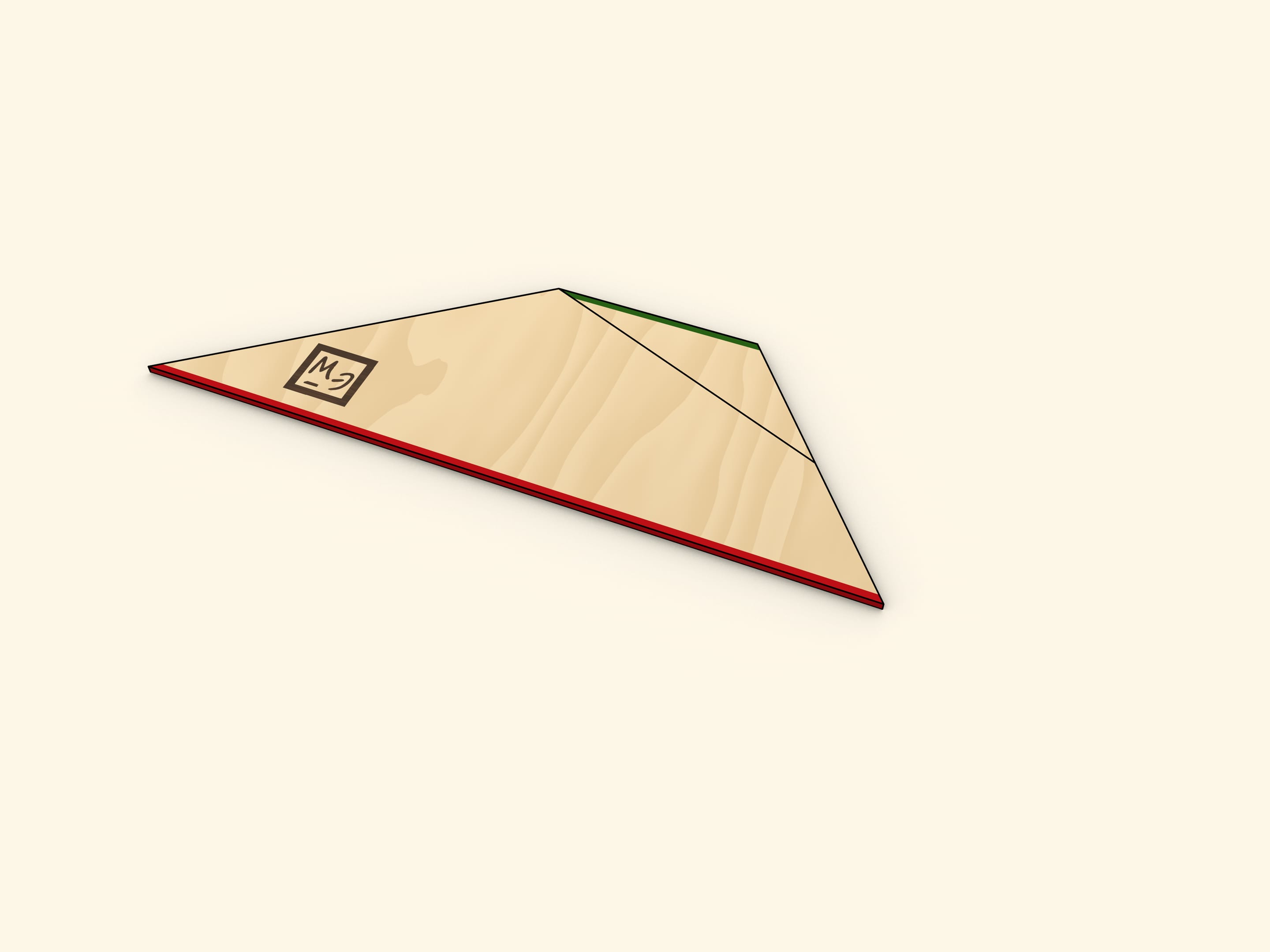
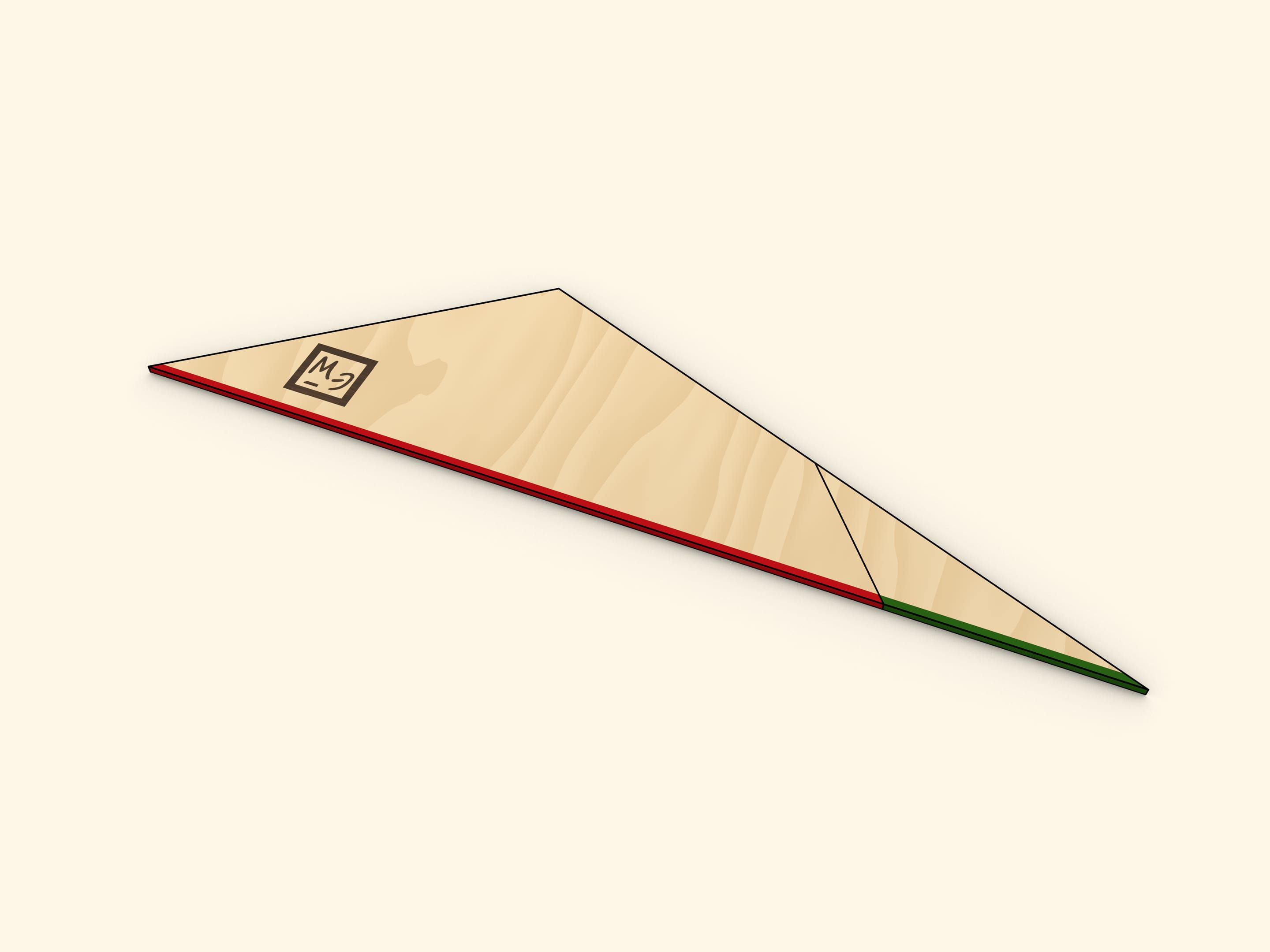
Cut the triangle along the line connecting its vertex with the midpoint of the oppo­site side. Rotate the cut off triangle up to a moment when both bases of the trape­zoid are along the same line. Make sure that in this the two halves of the cut side also lie on the same line, so indeed that forms the triangle.

One of the sides of the triangle obtained is as long as the sum of trape­zoid's bases' lengths, and the alti­tude dropped at that side is as long as the trape­zoid's height.

One of the methods of finding the area of a triangle is finding the half of a product of a side length and the length of an alti­tude dropped at that side. Using this method gives the familiar formula for the trape­zoid area.

Both models can be built from an approx­i­mately 10 mm thick wooden board. For the conve­nience of demon­stra­tion, the two parts it was cut into can be attached together with the help of magnets.