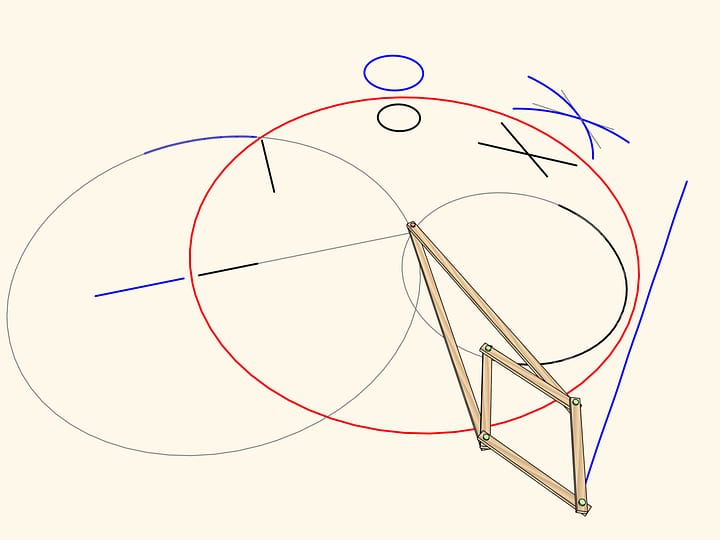
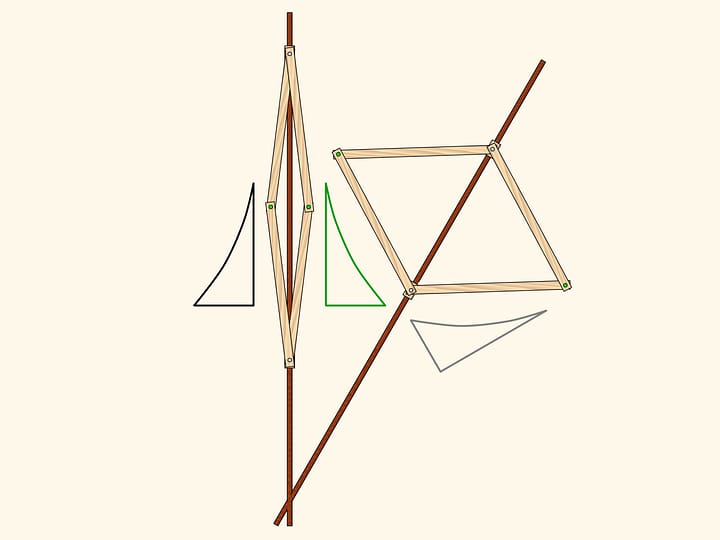
With two other classical problems, doubling the cube and squaring the circle, this problem came from Ancient Greece and was occupying human minds for centuries. By the way, even ancient mathematicians guessed that this problems can not be solved using only compass and straightedge, which was proved later. Attempts to extend tools lead to the first studies of conic sections, complicated curves and building interesting devices.
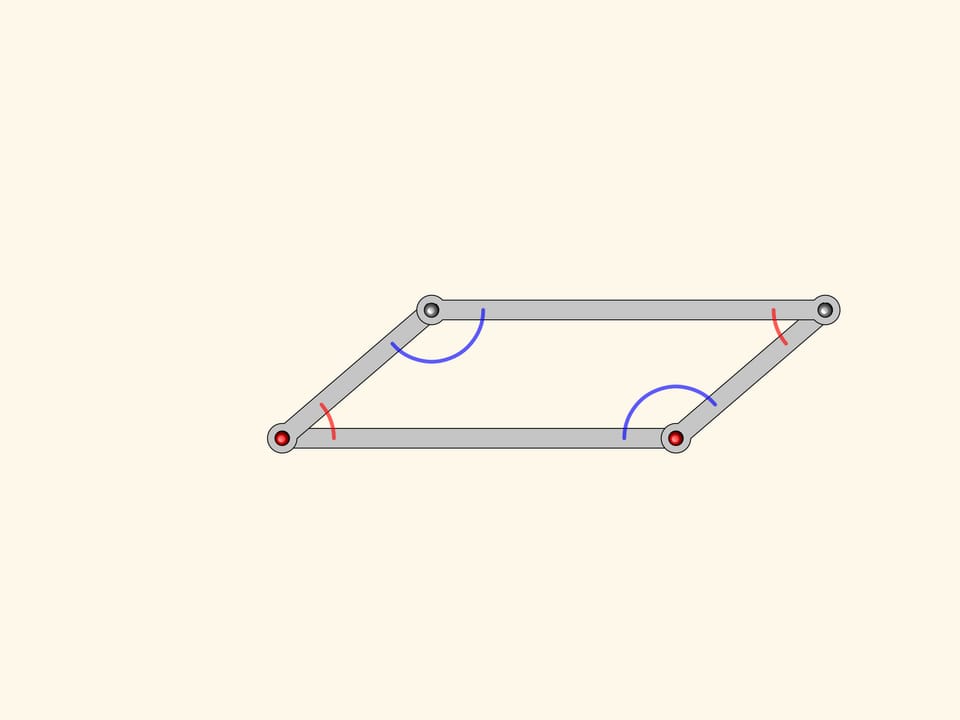
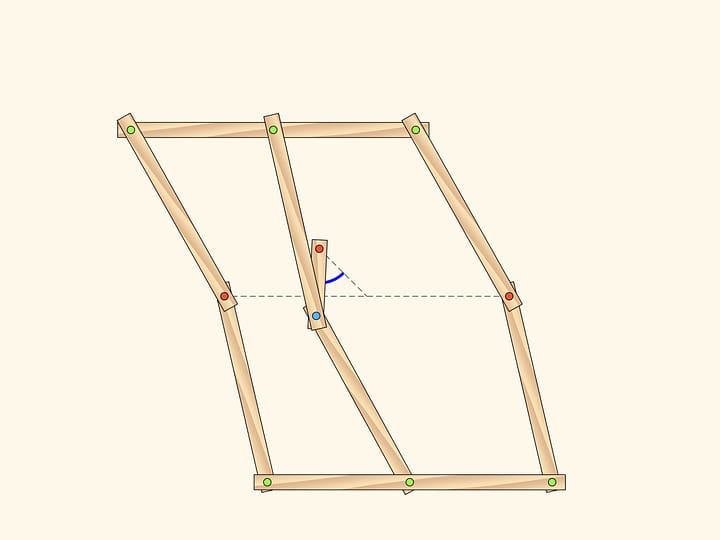
Consider a linkage being a parallelogram with two fixed hinges. You remember from school that opposite angles of a parallelogram are equal. This is true for every parallelogram, for any state our mechanism as well.
Are you sure that for any?
Our system has a special point when all edges are anti-parallelogram.
Sir Alfred Bray Kempe 1849—1922
This special feature of the mechanism was not considered in the reasoning of Alfred Kempe who proved in 1876 a theorem telling that there is a mechanism that can only falsify your signature and do nothing else. To be more precise, every bounded part of a plan algebraic curve is a hinge trajectory for some plane linkage. The theorem itself is true, but the mistake in Kempe's proof was found only in 1984 and corrected by the end of the XX century.
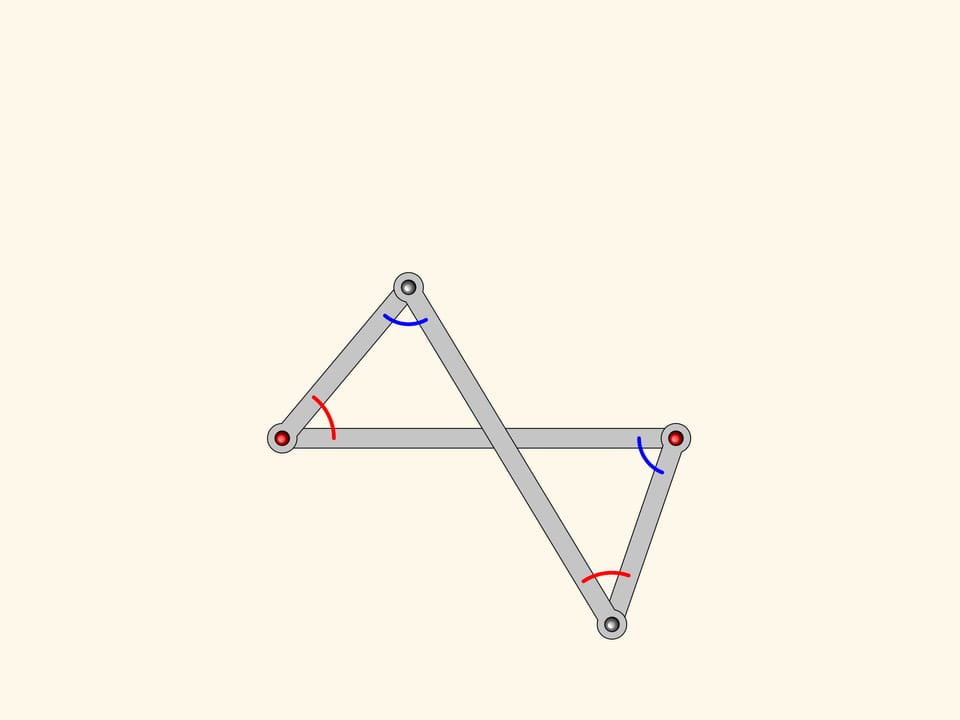
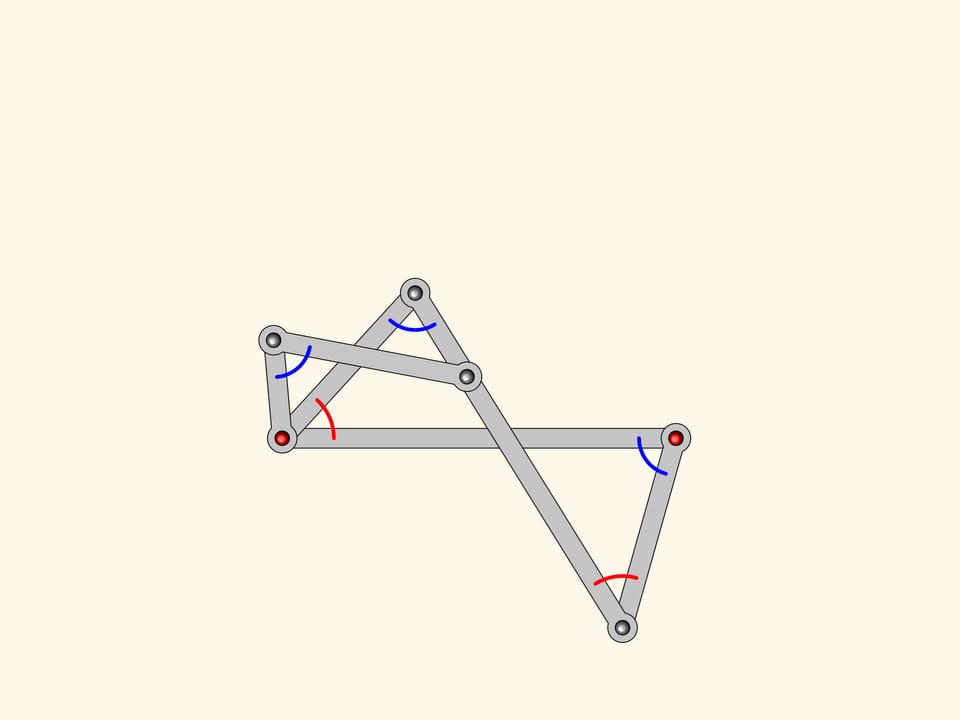
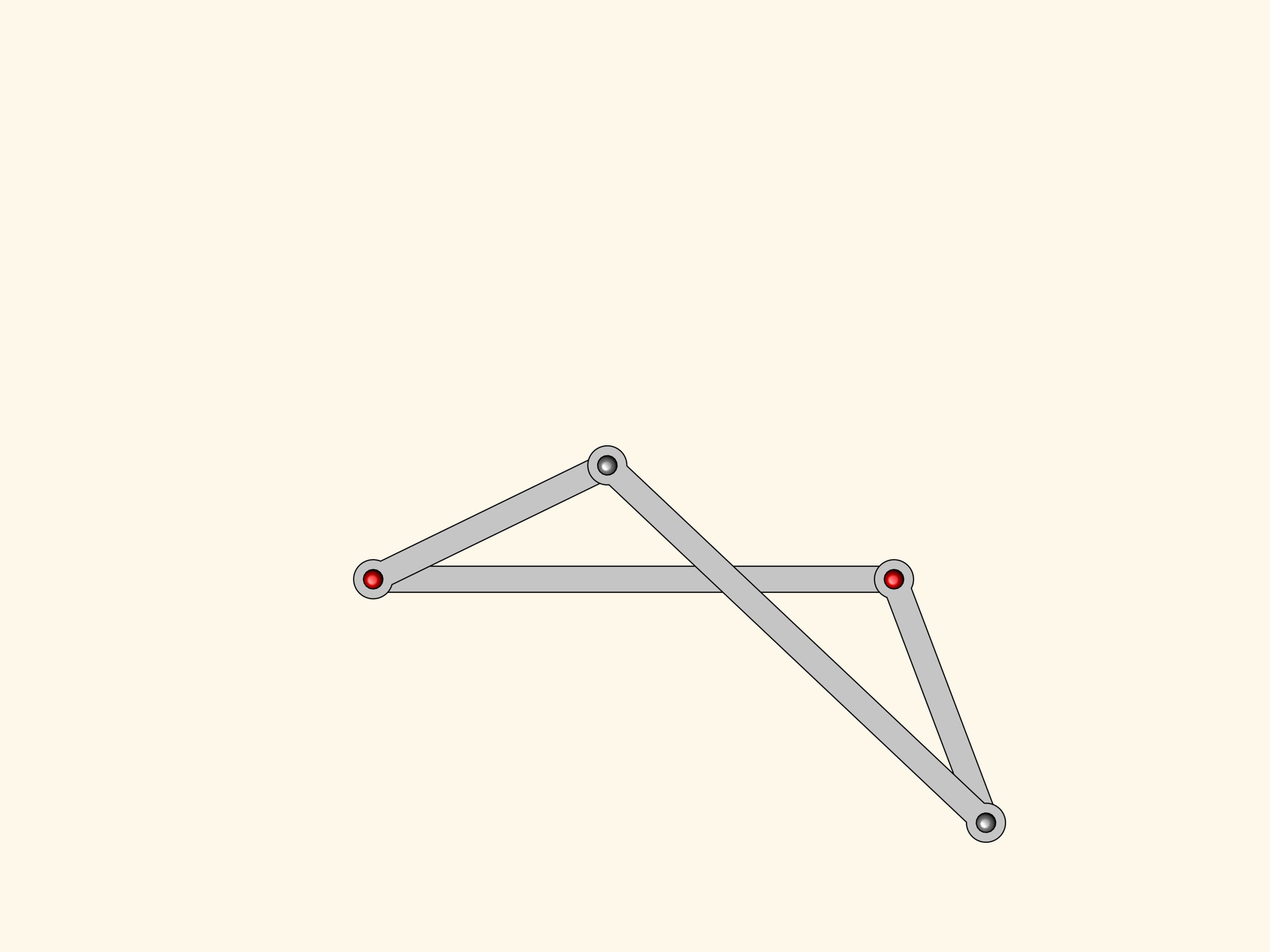
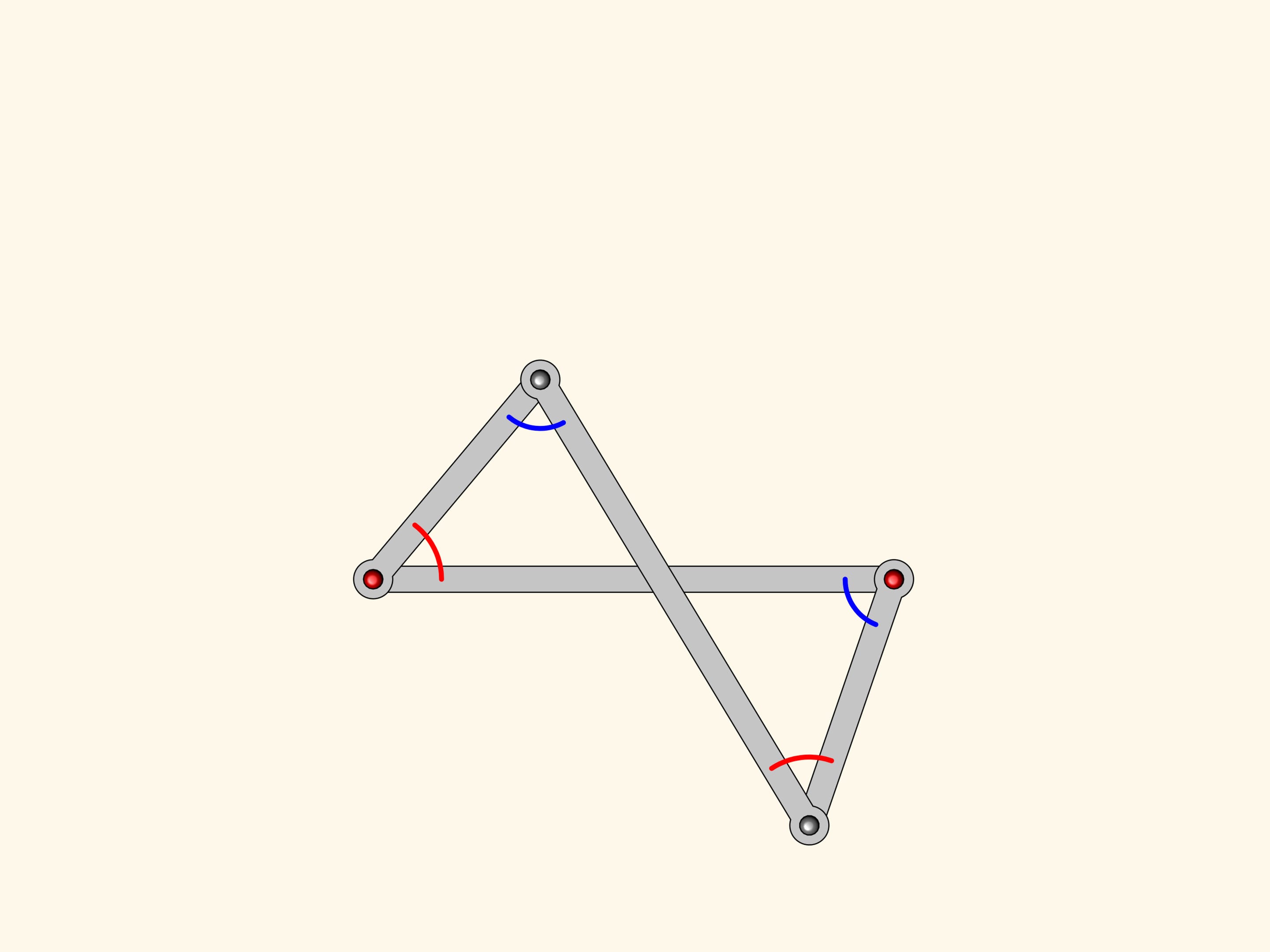
Anti-parallelogram inherits from parallelogram the equality of opposite sides. It turns out that there is a constraint on the angles to: they are pairwise equal!
Attach a smaller parallelogram angles at the red hinge are also equal.
Stretching the directing lines we get a linkage one can use to draw a bisector of any given angle.
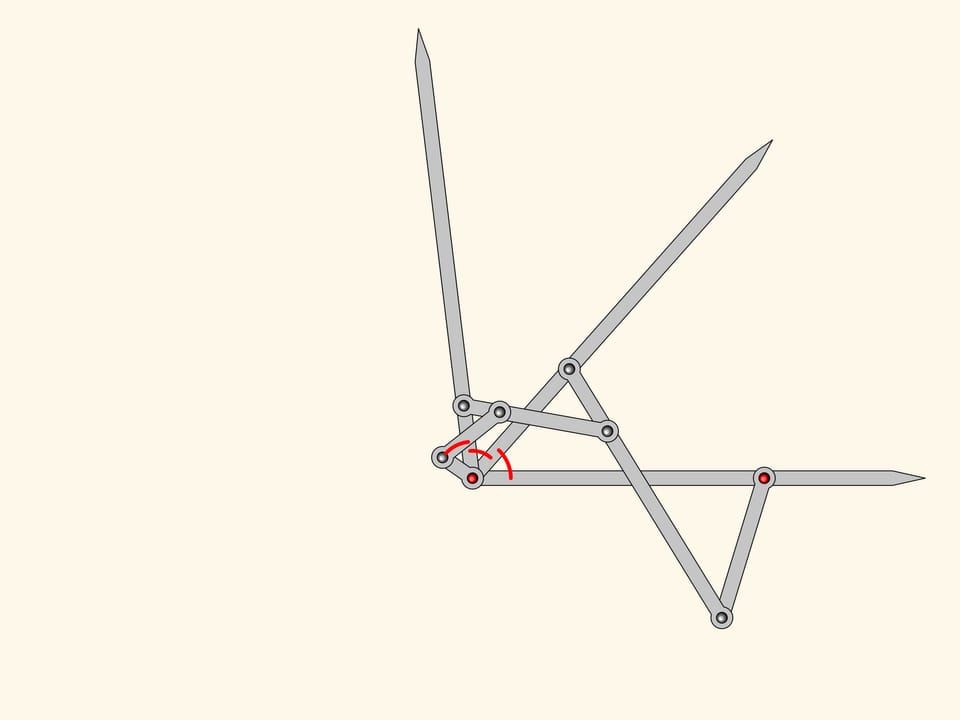
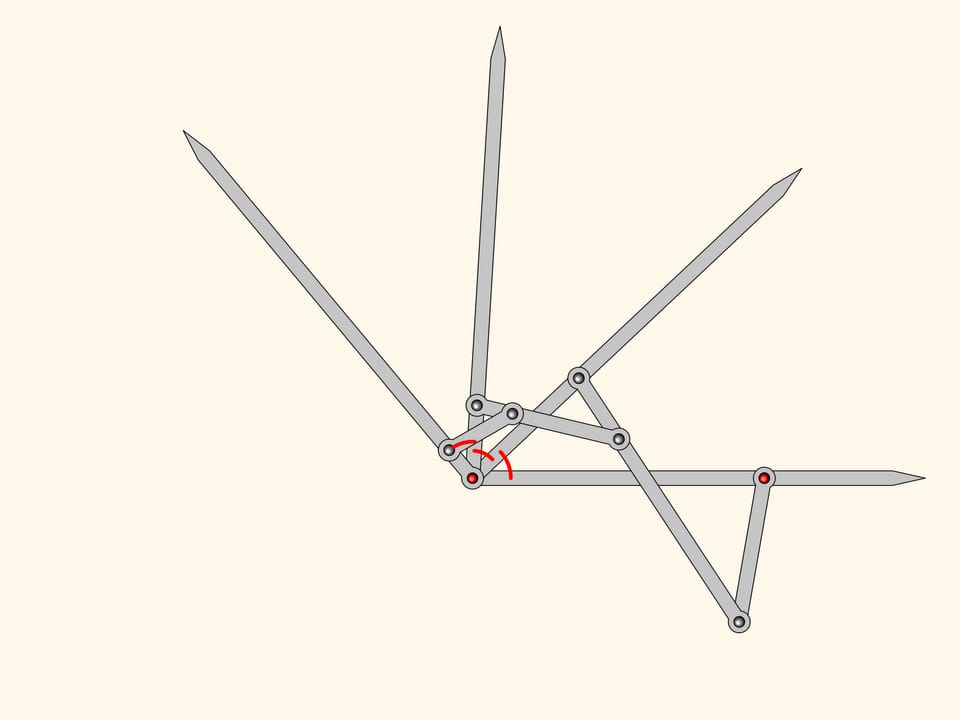
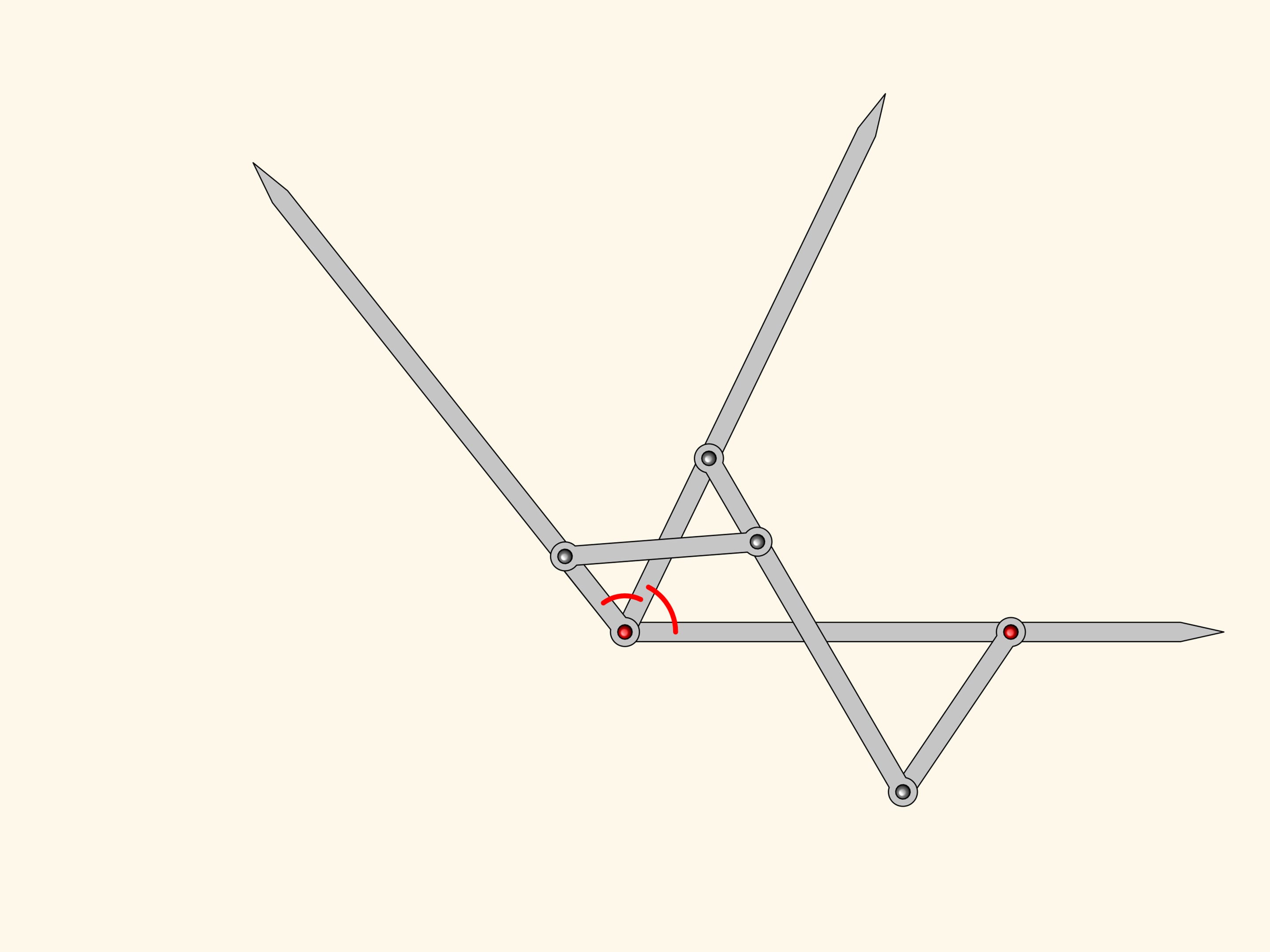
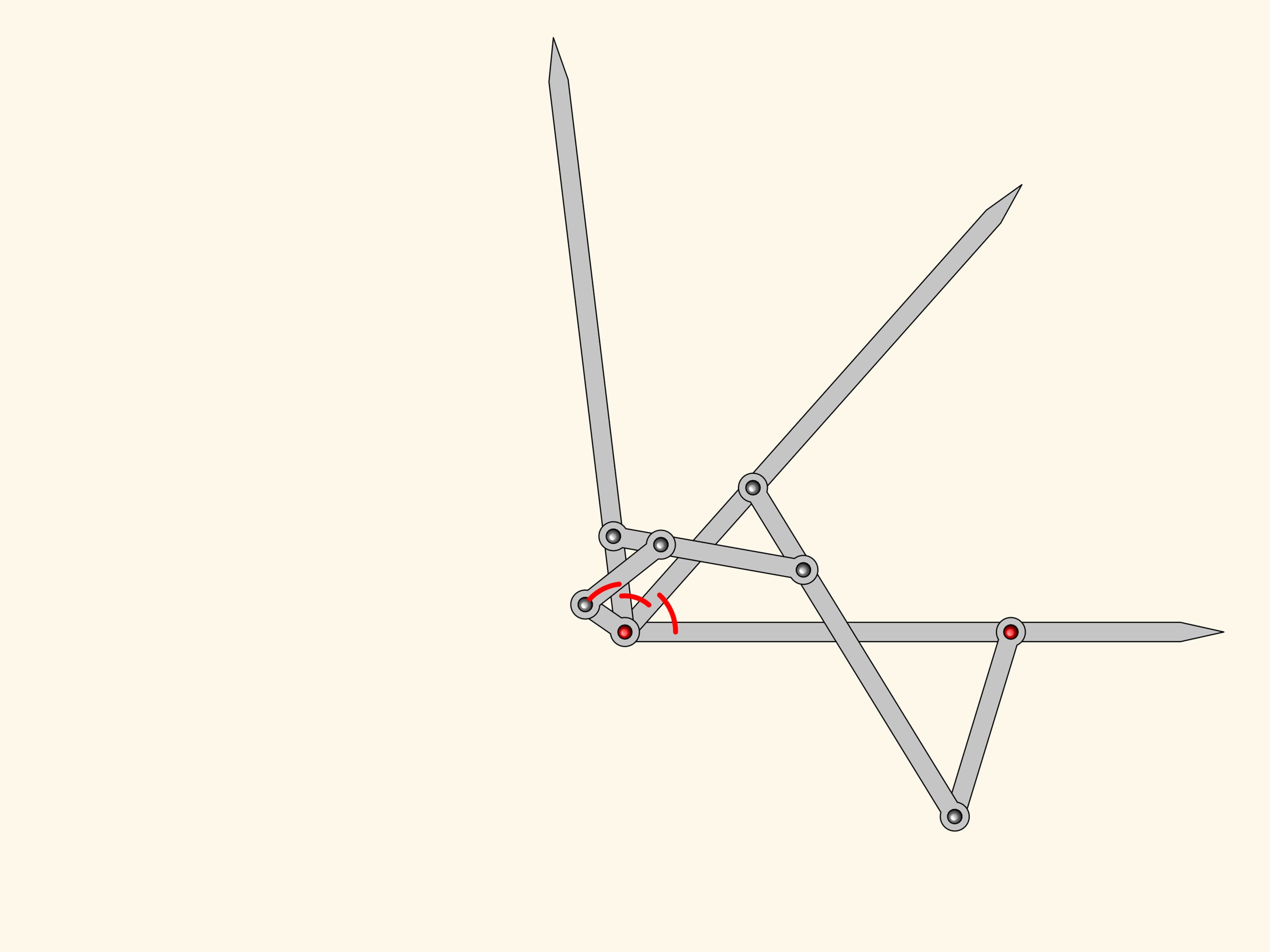
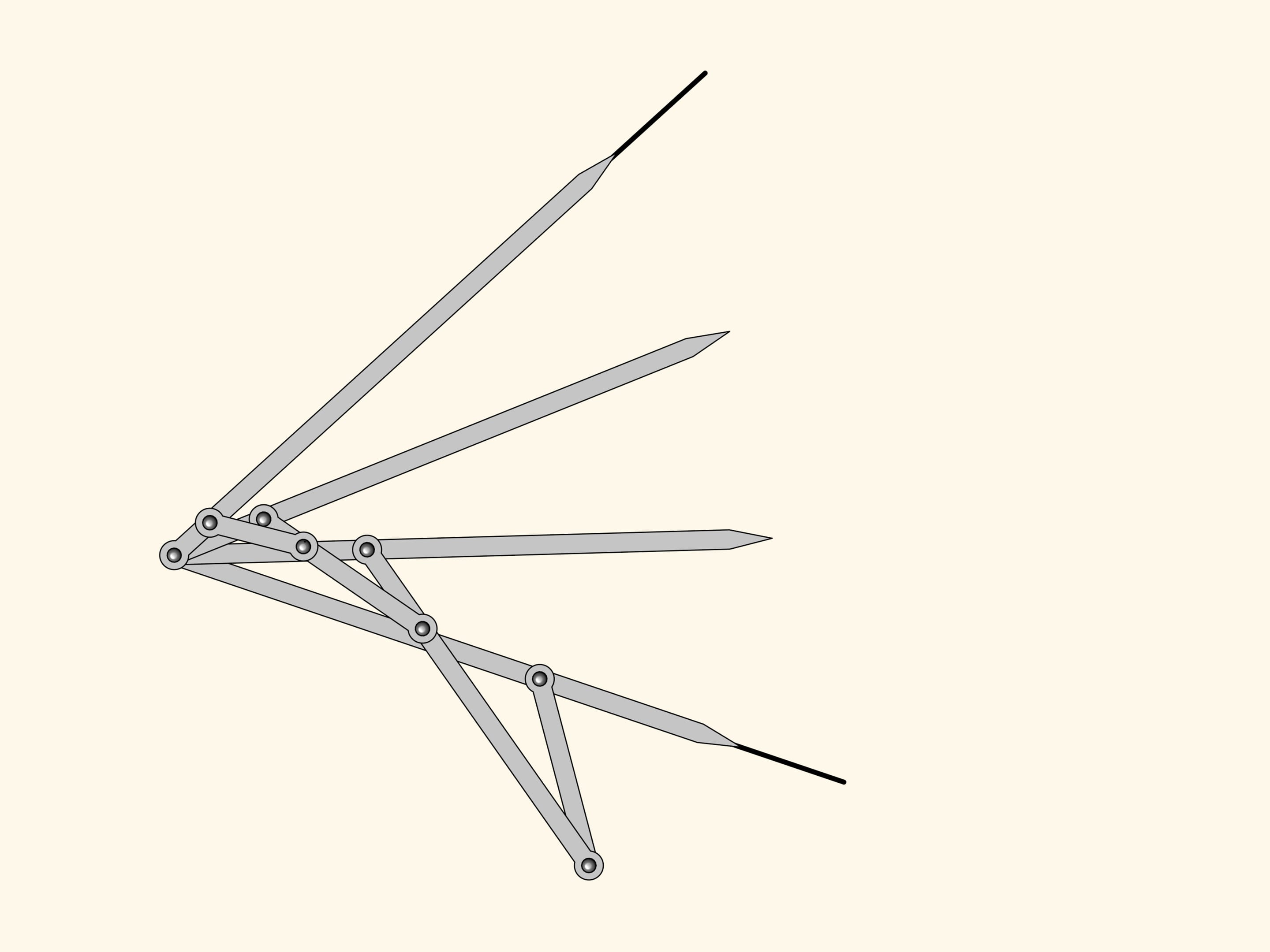
One can add equals the two we have already.
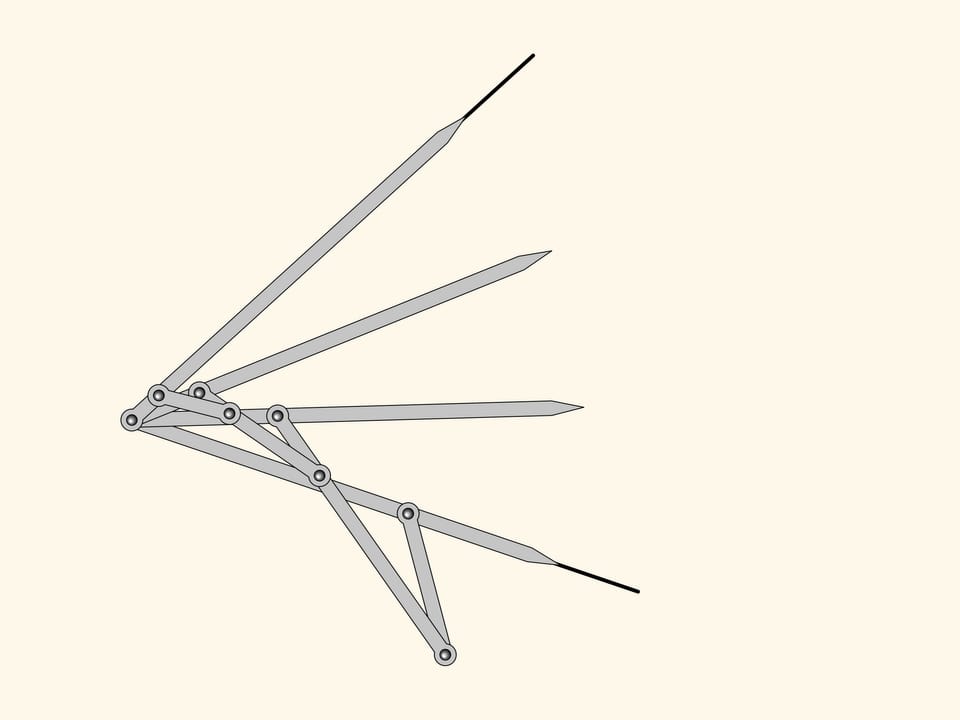
The plane linkage we get is an three equal parts!
This is where Kempe stops as for his proof of the signature theorem one needs a mechanism dividing an angle into three parts. However, it's evident that this algorithm can be iterated to obtain mechanisms dividing any given angle into any given number of equal parts.