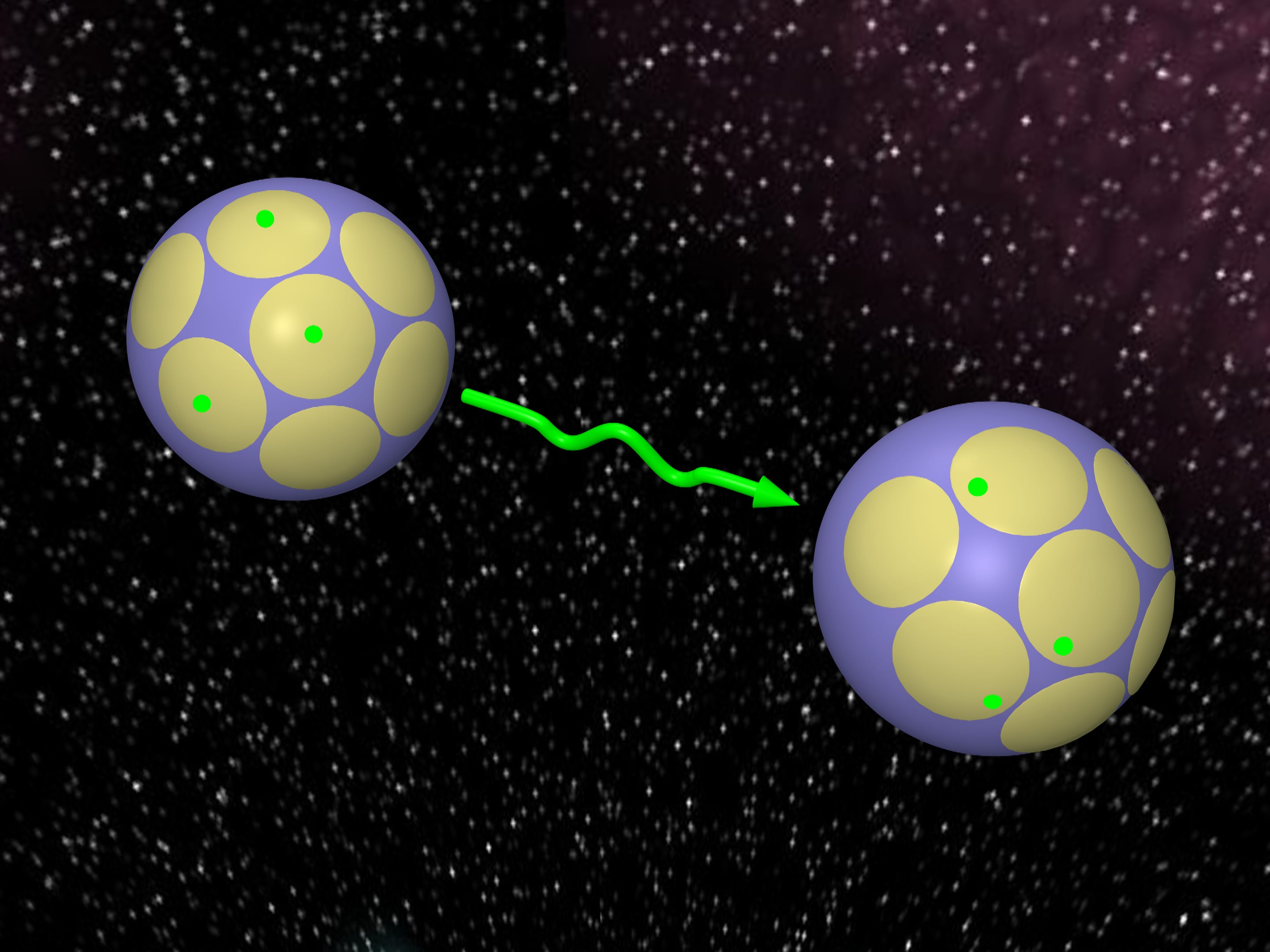
In reading this text or in downloading a film you may have used the solution of the balls contact number problem in 8-dimensional space.
How many equivalent spheres can be placed around a given sphere?
Let us consider a plane case. We have a touch an equal coin?
It is possible to dispose six coins in this manner with their centeres in the vertices of a regular polygon.
Is it possible to dispose more coins?
Each coin takes up an angle of 60 degrees. Complete angle can be divided into six such angles. This means that six is the greatest number.
This may be shown in a slightly another way. On the circumference of the central coin we consider the arc that is filled with one coin that touches the central coin. If you divide the length of the circumference by the length of this arc you will find out that there is room just for six such arcs.
Thus we have found the disposition of six coins and we have proved that this number is the greatest number.
The majority of extremal problems, that is problems of finding maximum and minimum, are solved just in this way. We give a certain construction and then we prove that it is the best one under conditions of a problem.
In our ordinary three-dimensional space the problem proved to be much more difficult.
How many identical billiard-balls is it possible to arrange around a given billiard-ball of the same radius.
Twelve balls could be placed at the possible to roll the balls on the central ball.
Whether more than 12 balls could be placed? This question was the subject of a celebrated discussion between the Scottish scientist David Gregory and Isaac Newton in 1694. It was Newton who studying astronomic questions noticed that 12 balls could be placed at the vertices of an icosahedron.
David Gregory generalized the upper estimate of the amount of coins placed around a given one. He calculated the square of a spherical cap occupied by one ball and divided the square of the central sphere ball by the square of this cap. Conduct calculation and you will be surprised that the answer is almost 15. As this number turned out to be less than fifteen it goes to prove that 15 balls could not be placed. However, Gregory could not guess that it is impossible to dispose even 13 balls.
It took 200 years to prove for the first time, that contact number in three-dimensional space is 12.
The contact number problem is also solved in 4-dimensional, 8-dimensional and 24-dimensional spaces. The contact numbers are 24, 240, and 196560 respectively. Balls are placed at the points of the chess lattice, Korkin-Zolotarev lattice and Leech lattice. The last advancement in this problem (solution in the 4-dimensional case) has been obtained by Russian mathematician Oleg Musin.
This beautiful and it would seem purely mathematical problem is a special case of a spherical code problem. It has many important applications in technique concerned with information transmission. In particular, error-correcting code, used in modems, is closely related with contact number problem in 8-dimensional Euclidean space.
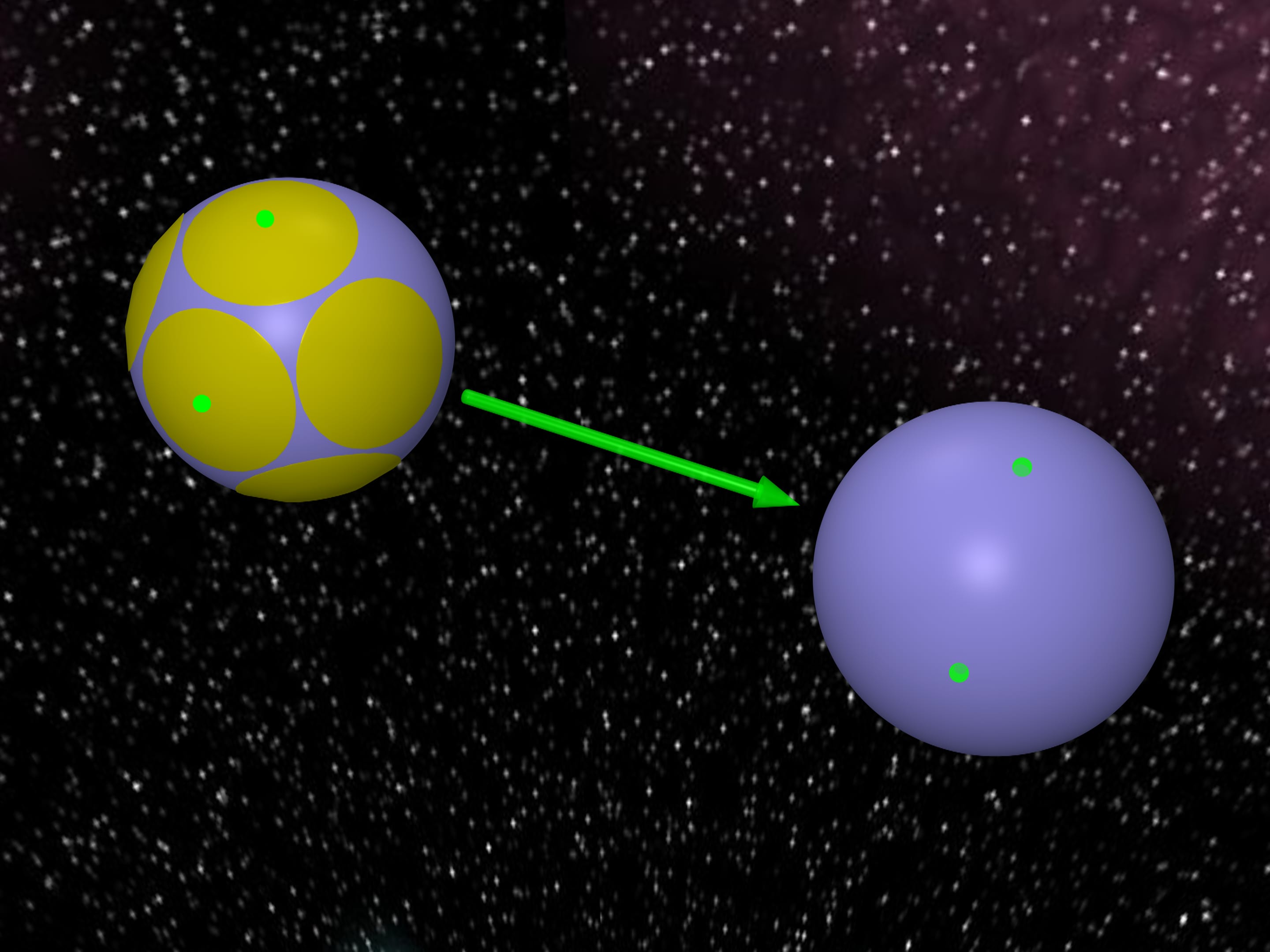
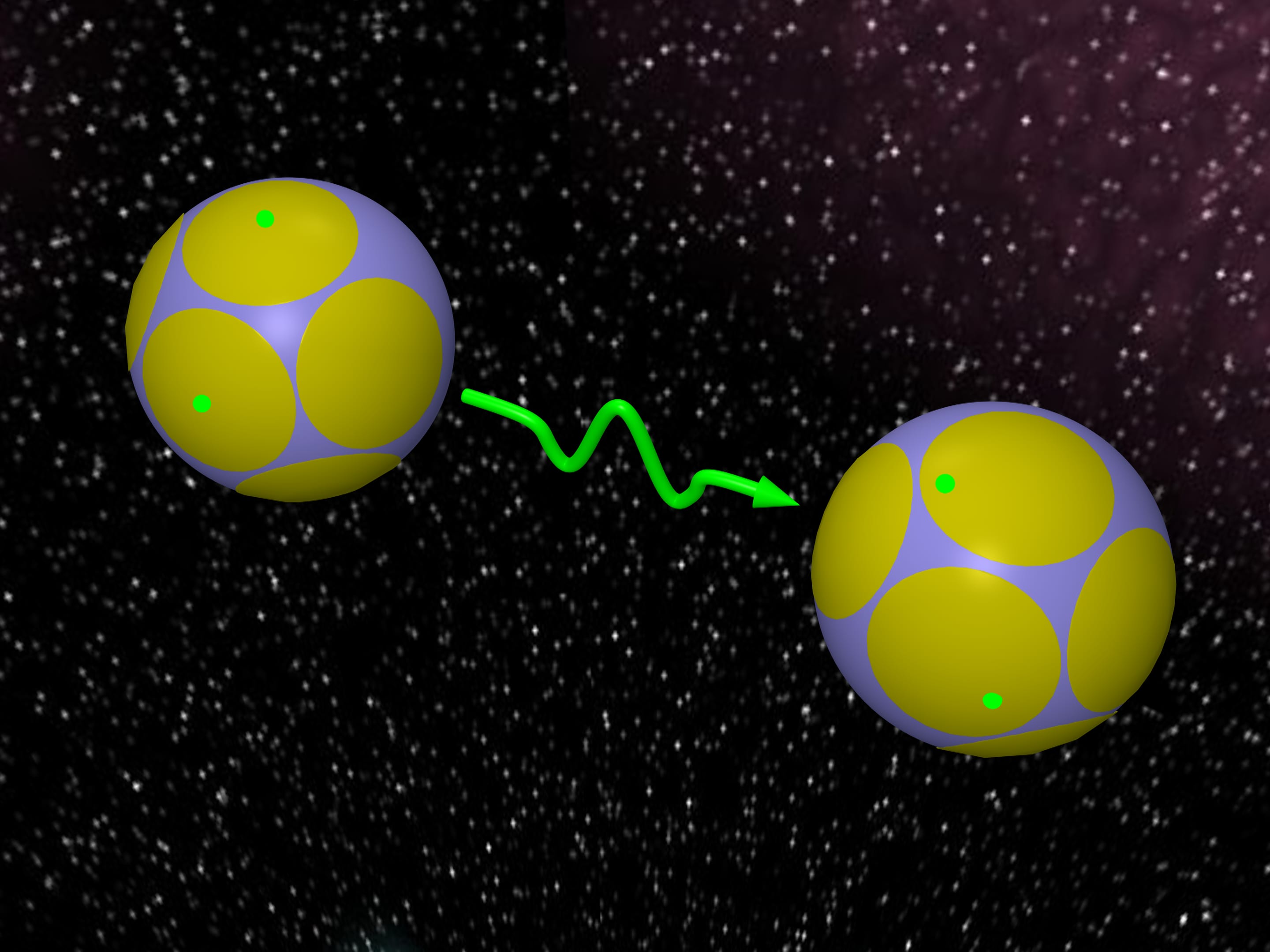
Some power restrictions arise during transmission of information over a distance, for example, from the Earth to a satellite. To put it mathematically, these restrictions mean that transmitted signals are points of a sphere in Euclidean space. There is a recovered too.
If we know that the distortions during transmission are small we can consider caps of a smaller size.
If we want to transmit more information that is to have as many various words as possible we come to the problem: how to arrange as many spherical caps of a given size on a sphere as possible.
This creates, in balls language, the following problem: how many equivalent balls can simultaneously touch a given ball of another radius?
Open problem
In spite of a great applied importance of the spherical code problem, it is solved only in a small number of special cases, both in 3-dimensional space and in high dimensional spaces. The exact solution in the general case or even in some infinite series of cases has not yet been discovered.