Ellipse ⁠

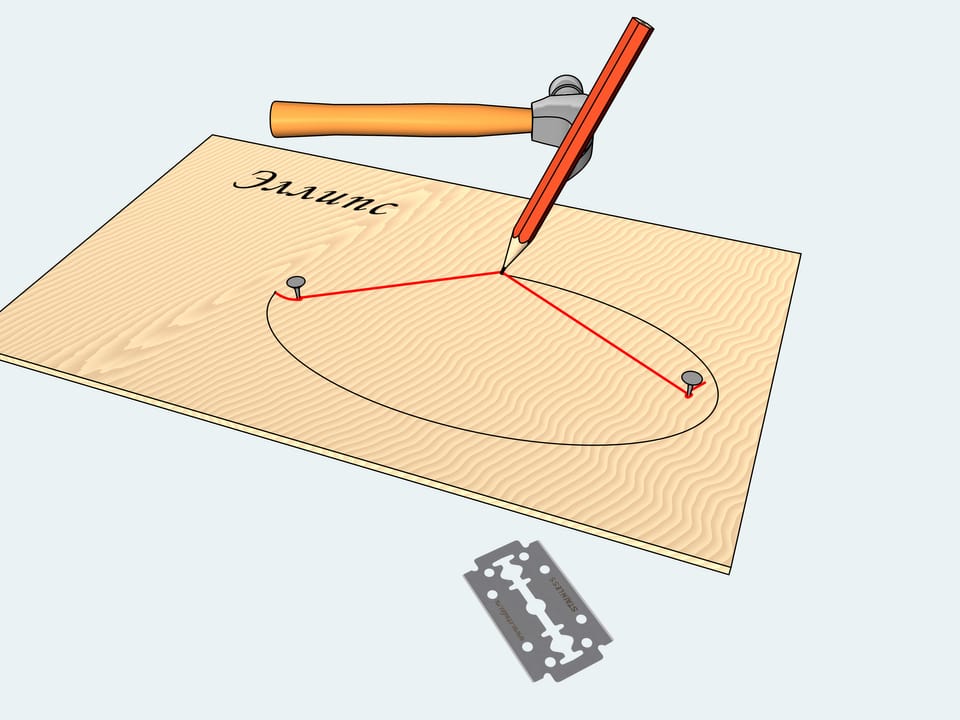
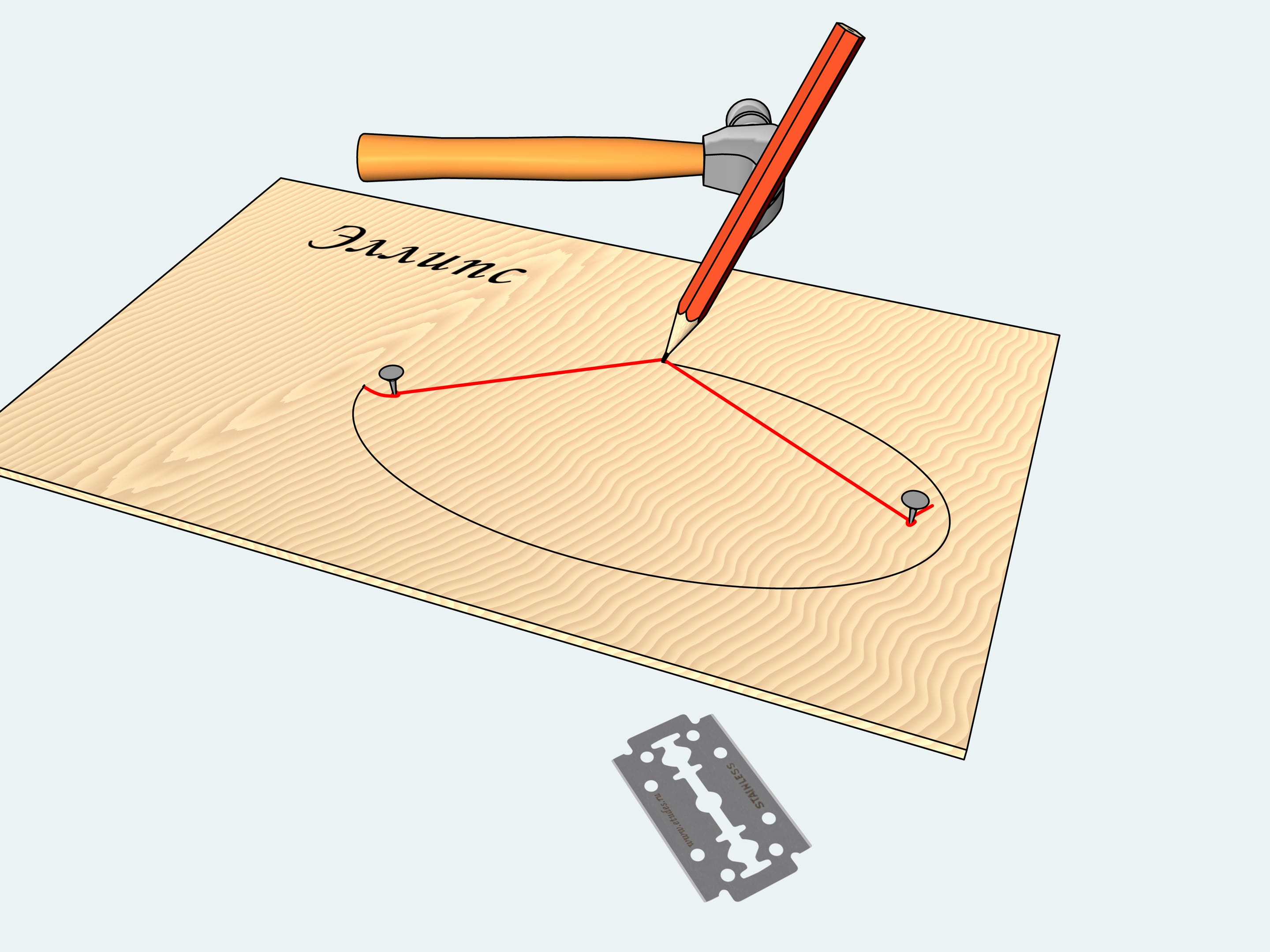
Every­thing you need in everyday life to draw a curve that in math­e­matics is called "ellipse" is here. A plank, two nails, a hammer, a string, a blade and a pencil.

Let's drive nails in arbi­trary points of our plank. Then, tie the string to the nails so that it is not tight. The length of the string doesn't matter, just cut off the unnec­es­sary ends with the blade.

Stretch the string with the pencil and start moving it to the left and to the right so that the string stays tight.

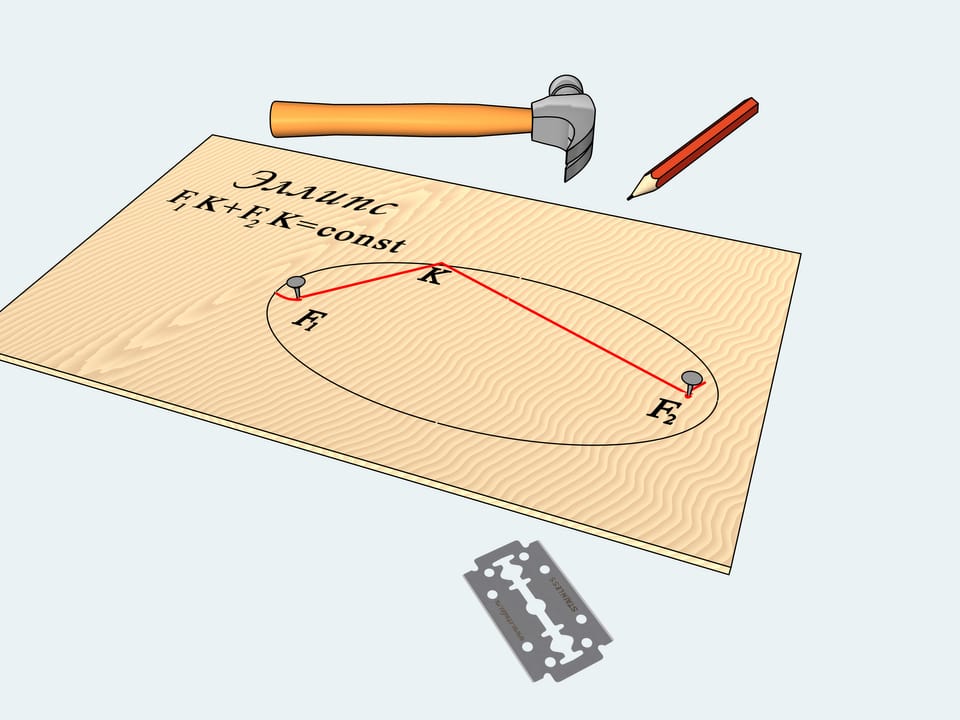
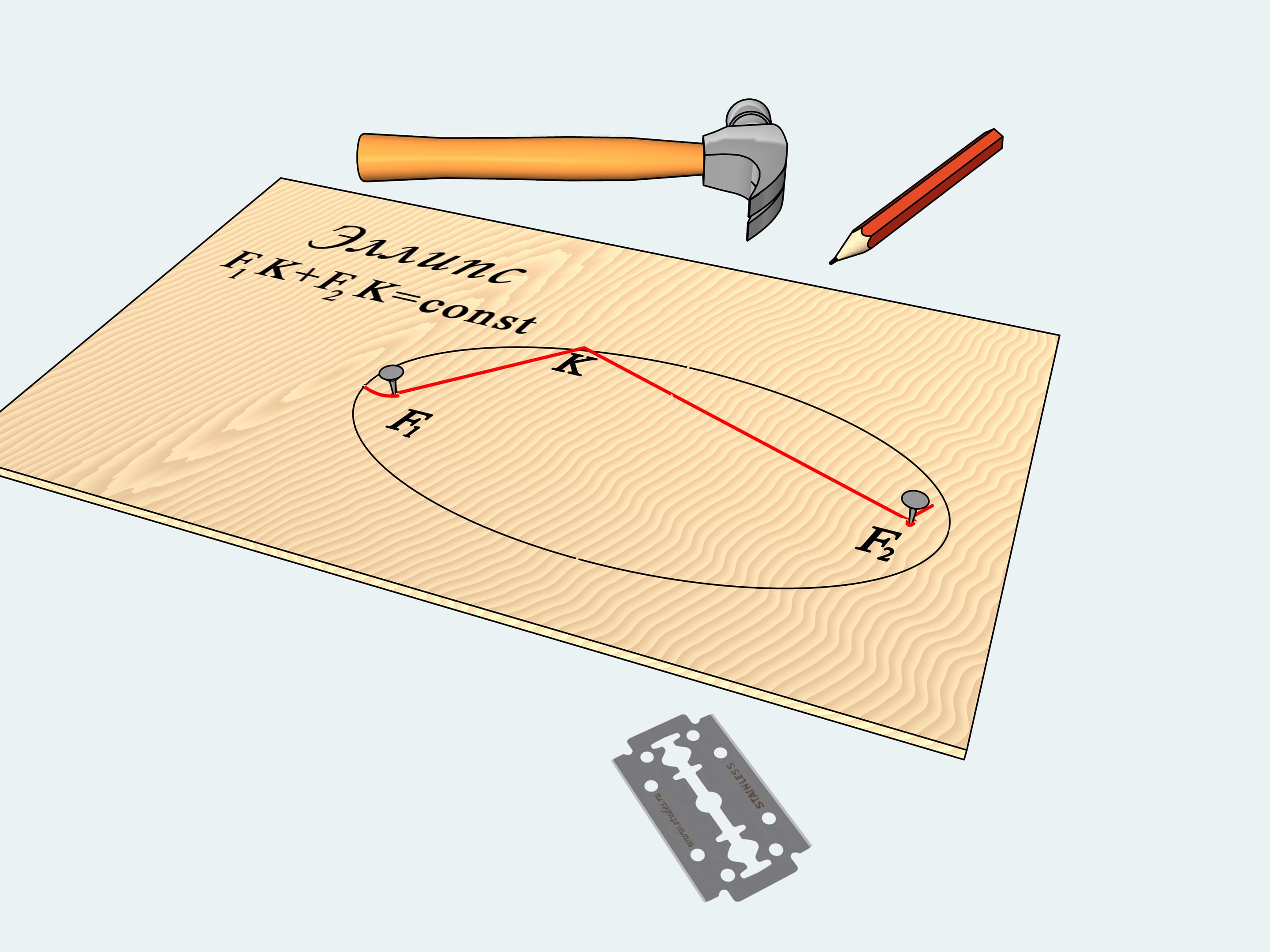
What does this have to do with some math­e­mat­ical notions, you might say. It turns out that the curve we have drawn is called ellipse in math­e­matics: it's a locus of points such that the sum of the distances from them to two fixed points that are called focal is constant. Indeed, the length of our string tied to the nails  — focal points $F_1$ and $F_2$ — remained constant, and so we drew an ellipse.

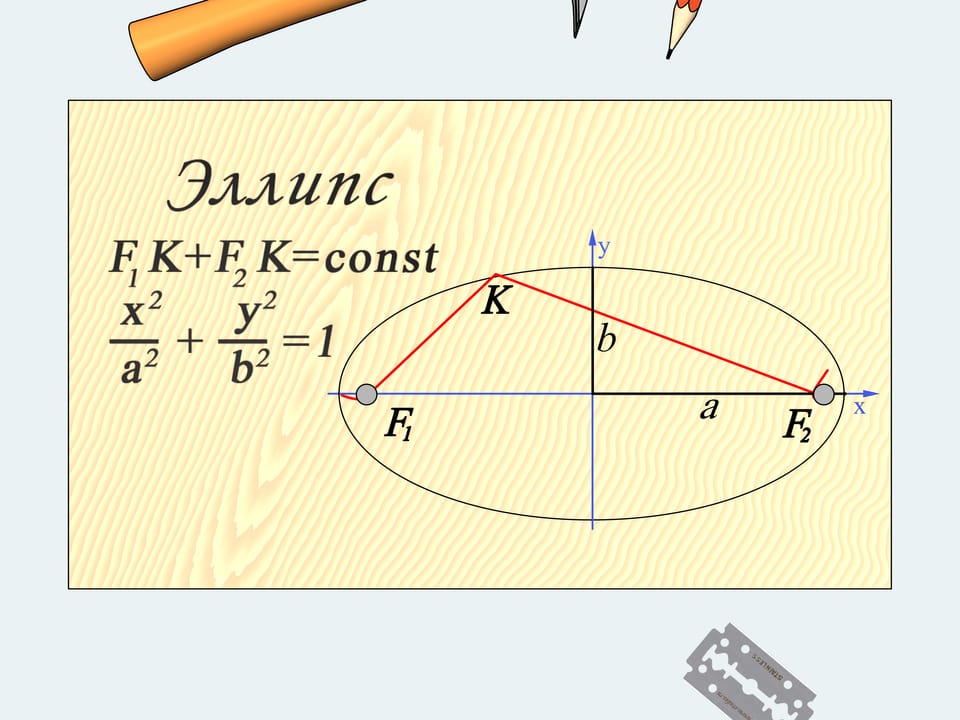
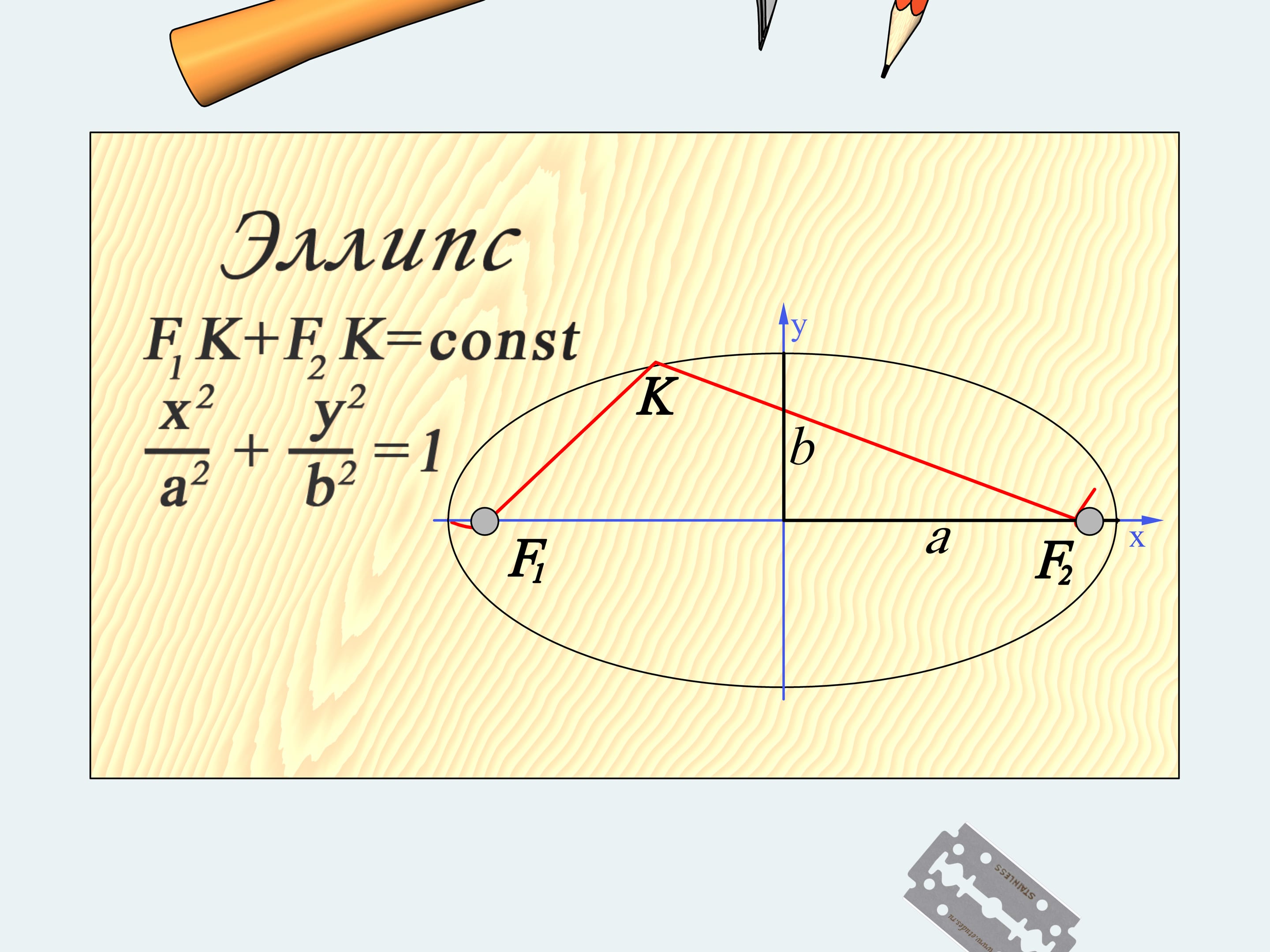
It's easier to write down the equa­tion defining an ellipse in the Carte­sian coor­di­nate system chosen so that, the $x$-axis passes through the focal points and the $y$-axis divides the distance between these points in two. The segments connecting the origin and the crossing points of the ellipse with two axes are called semi-axes. In chosen coor­di­nates the equa­tion defining our ellipse becomes the one we all know.