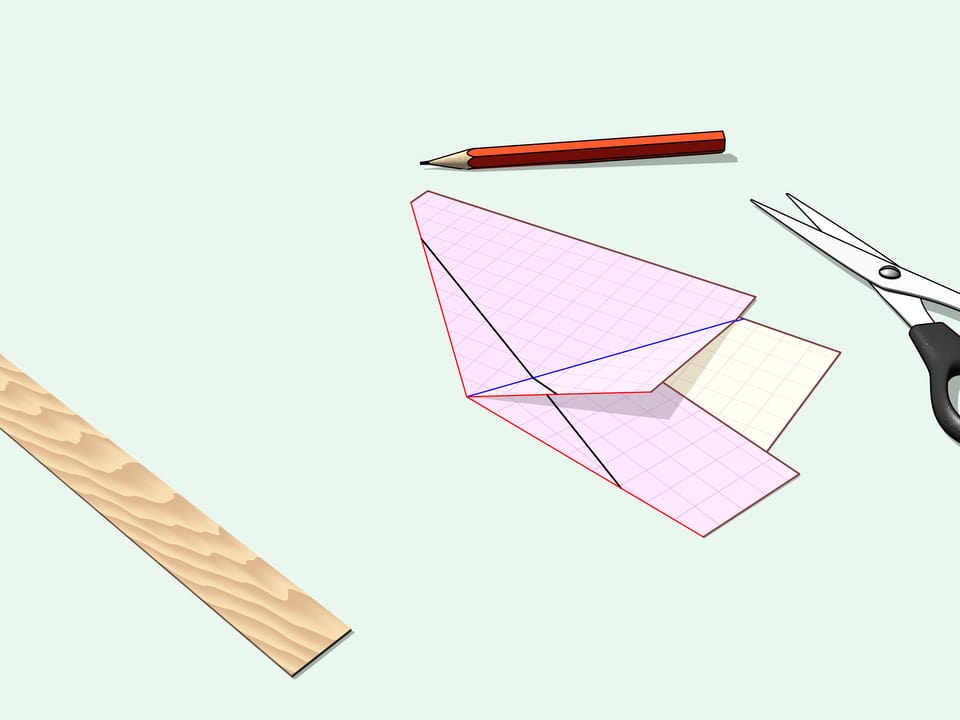
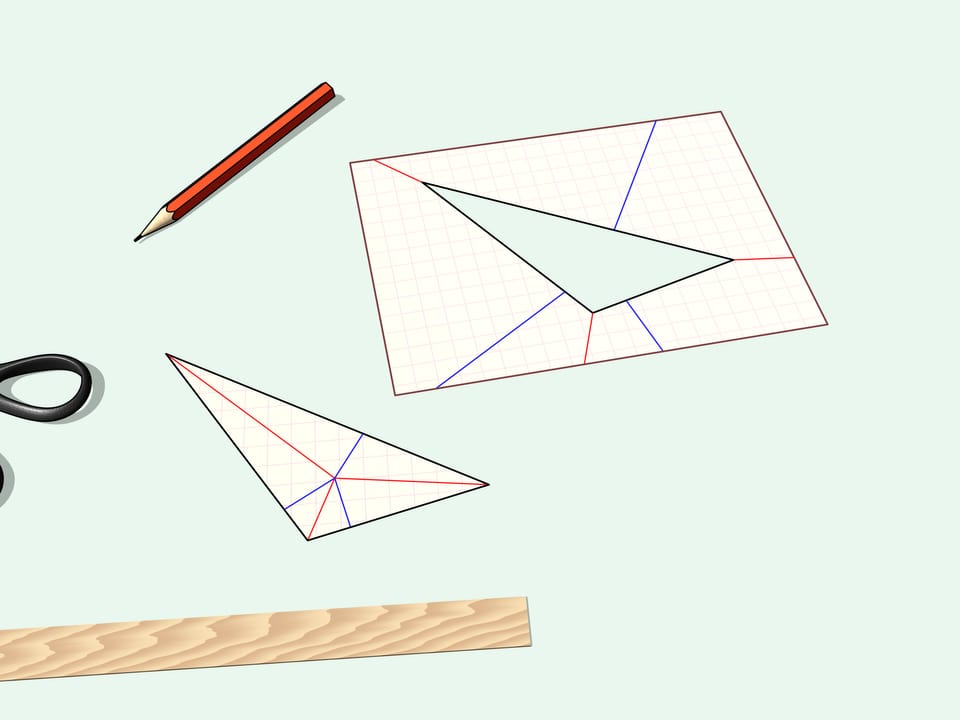
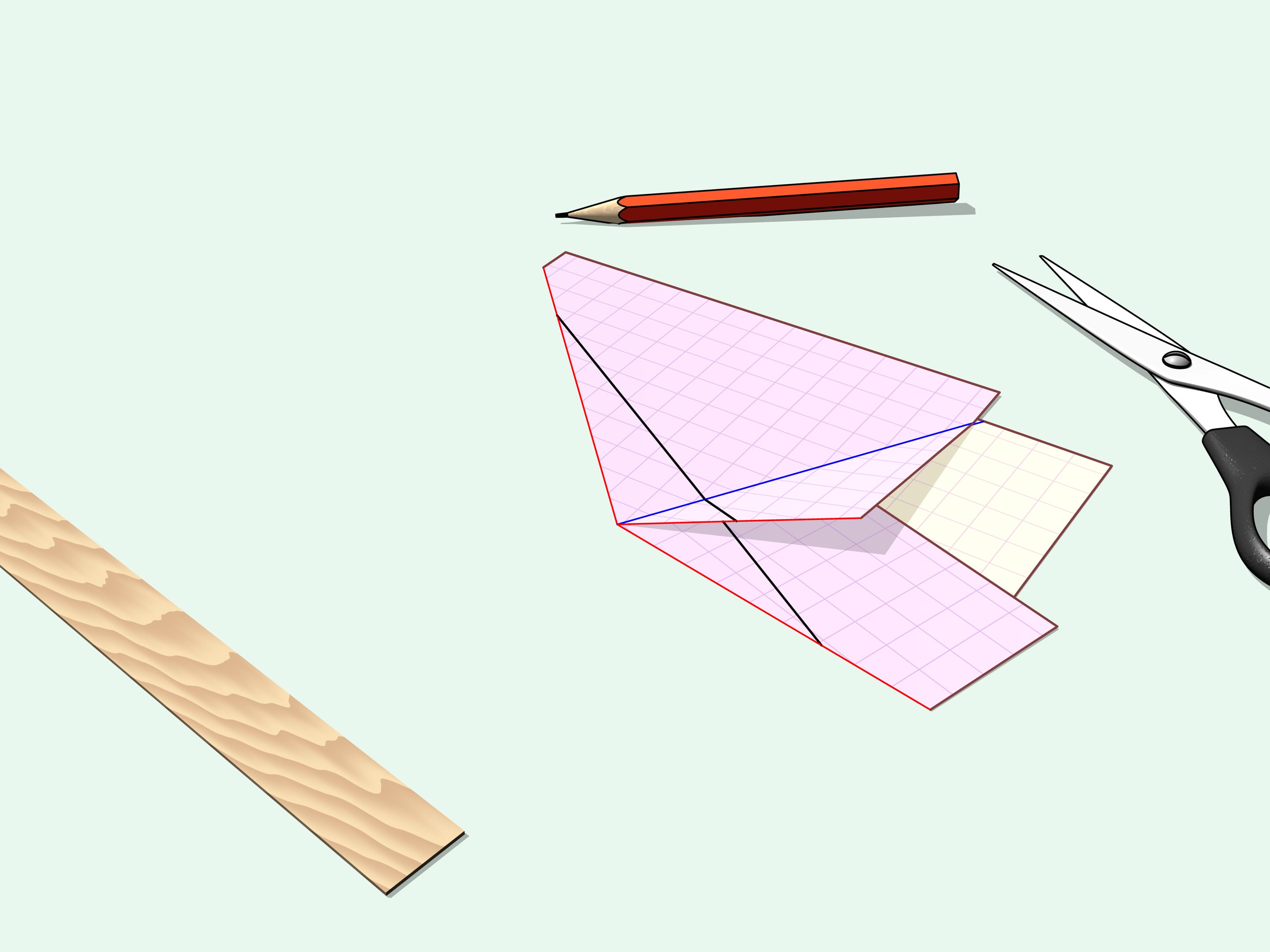
Let's take a sheet of paper and draw an arbitrary polygon. Is it possible to fold the sheet so that the polygon could be cut out with a single straight slit?
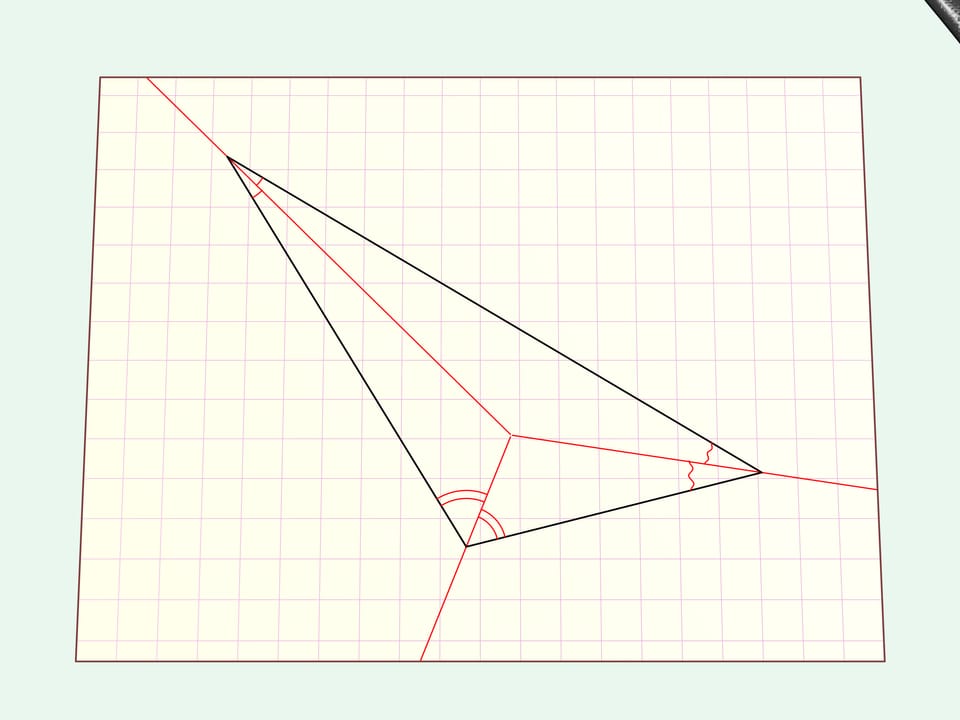
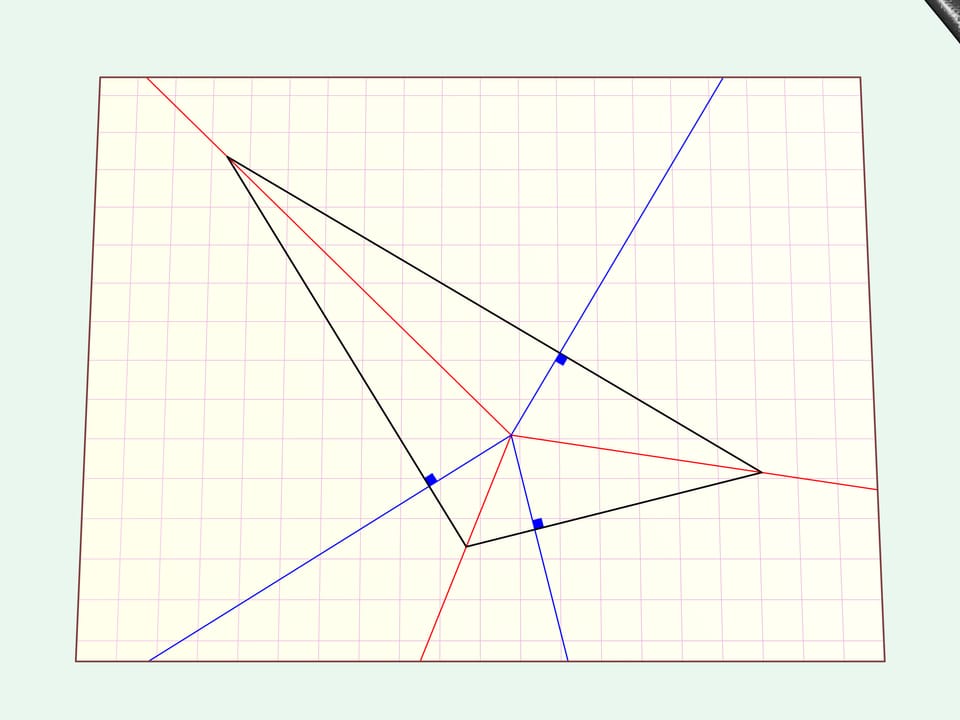
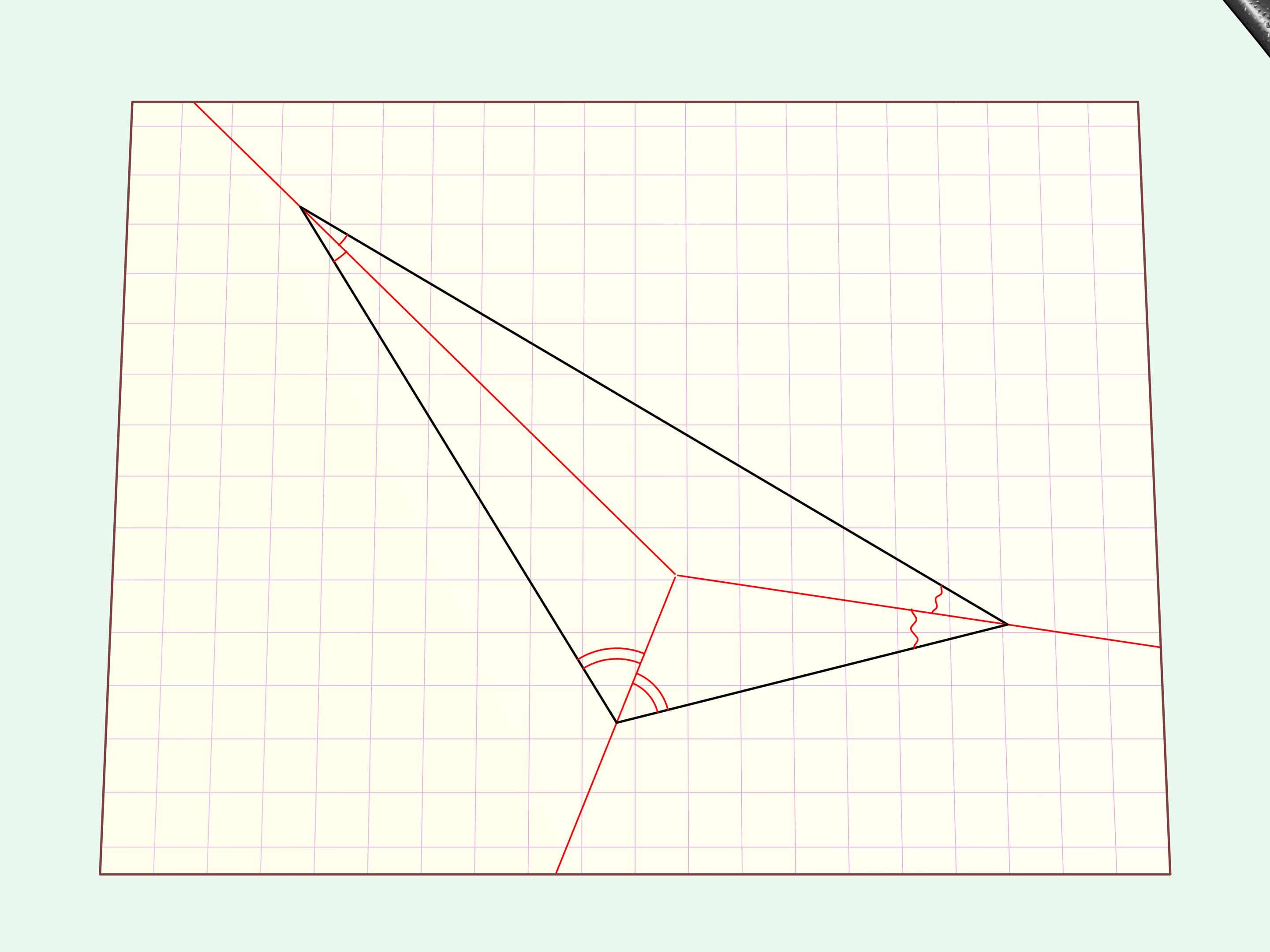
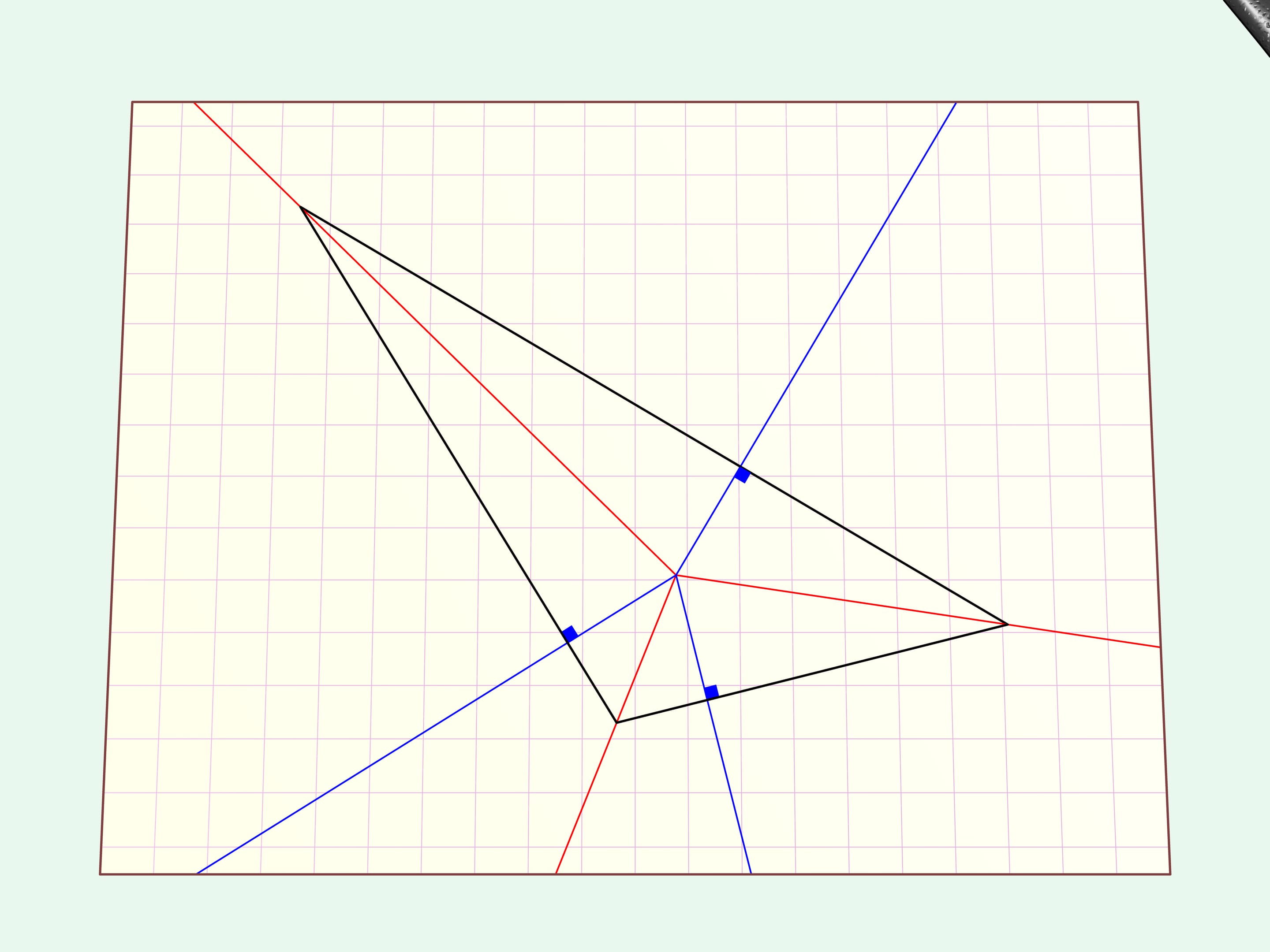
Consider the simplest case of an arbitrary triangle.
We draw a straight cut along it.
If you unfold the hole has the form of the initial triangle.
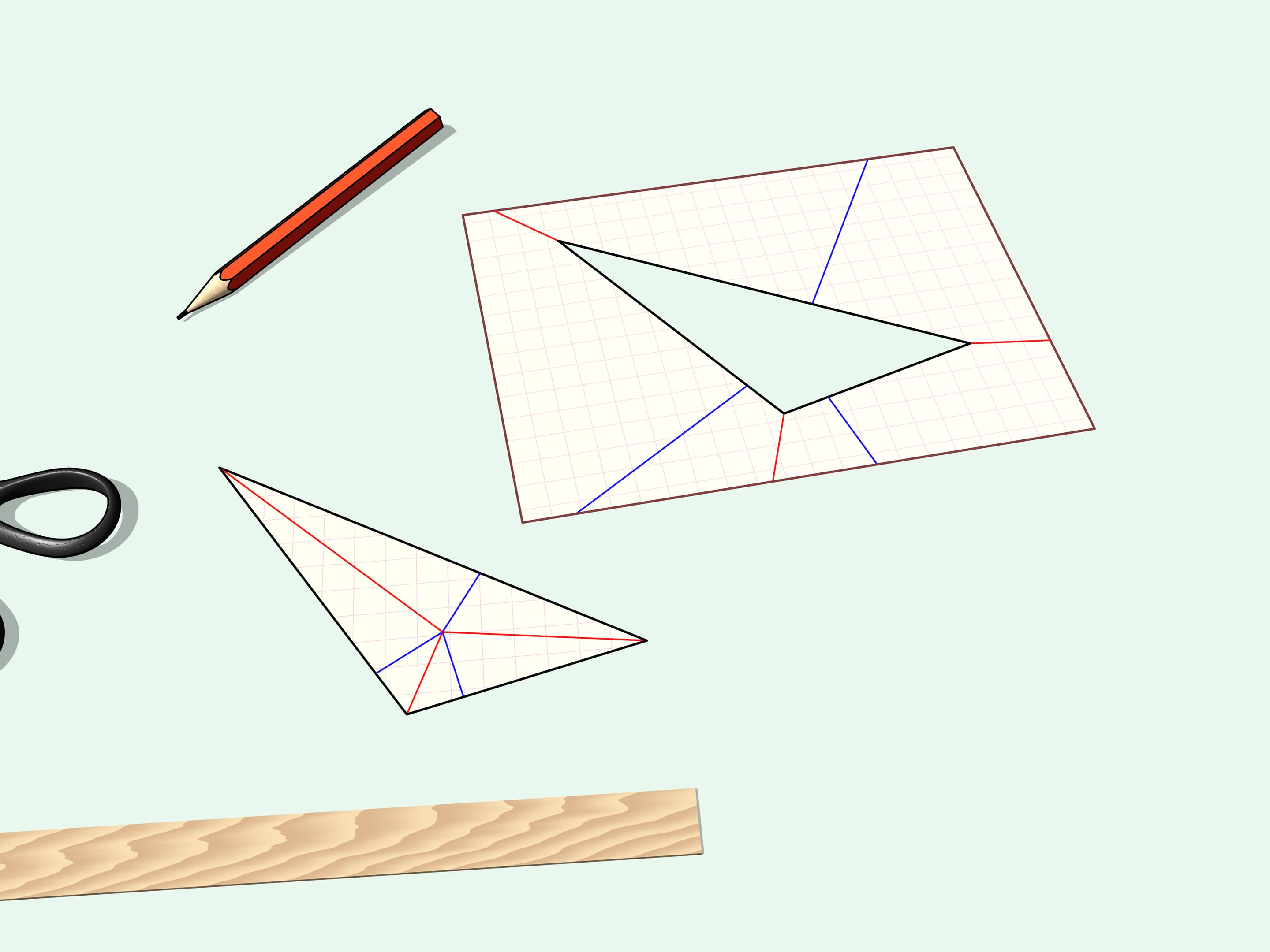
Let's draw a star.
It is also possible to cut out by one straight slit the polygon drawn in the beginning of the film. In 1998 the general theorem was proven.
Theorem
Given any polygon there exist a folding of a sheet of paper and a line on this folding such that scission along the line removes the (folded) polygon.
The proof of the theorem is algorithmical, that is the authors present a way to find a folding of a sheet of paper so that one straight cut creates any desired polygon.