Our planet, the Earth, has the shape of a ball flattened a bit at the poles. Quite a while people have used a ball-shaped globe to portray the Earth. But even more time we've been using a map.
A sphere is a surface of constant positive curvature and because of that it can't be placed on a plane without distortions. Methods to draw maps, cartographic projections, have a long and a very interesting story. Some of them are more familiar to us, some are used in very special questions and are barely seen in ordinary life, but it's a subject to another movie.
Some time ago there was a wonderful tradition to hang a map in the kitchen or in the children's room. Every piece of news had a visual geographical interpretation.
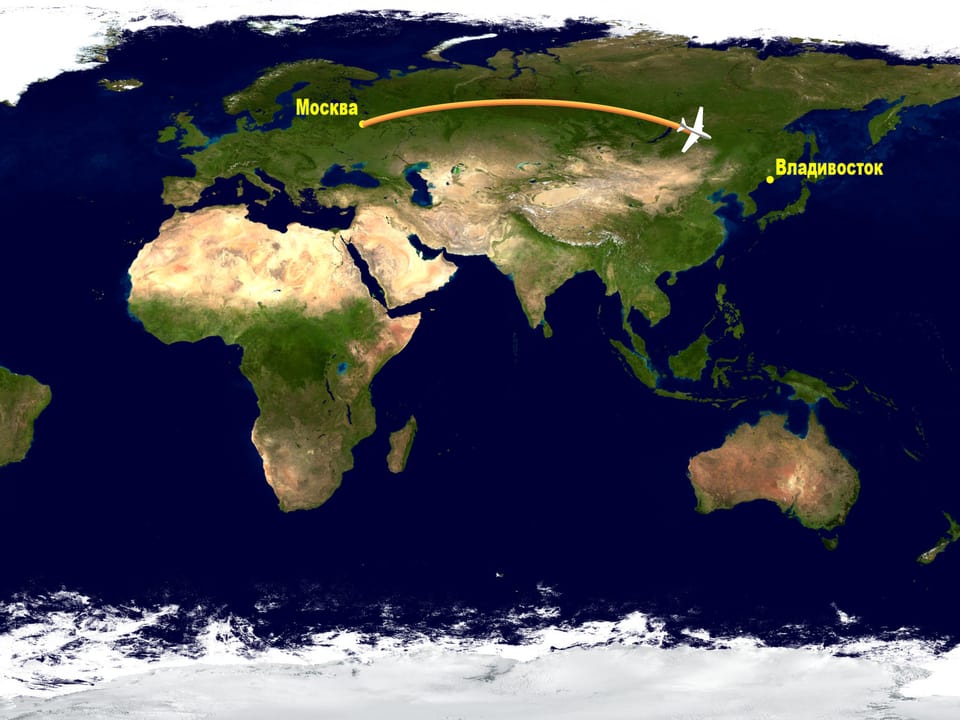
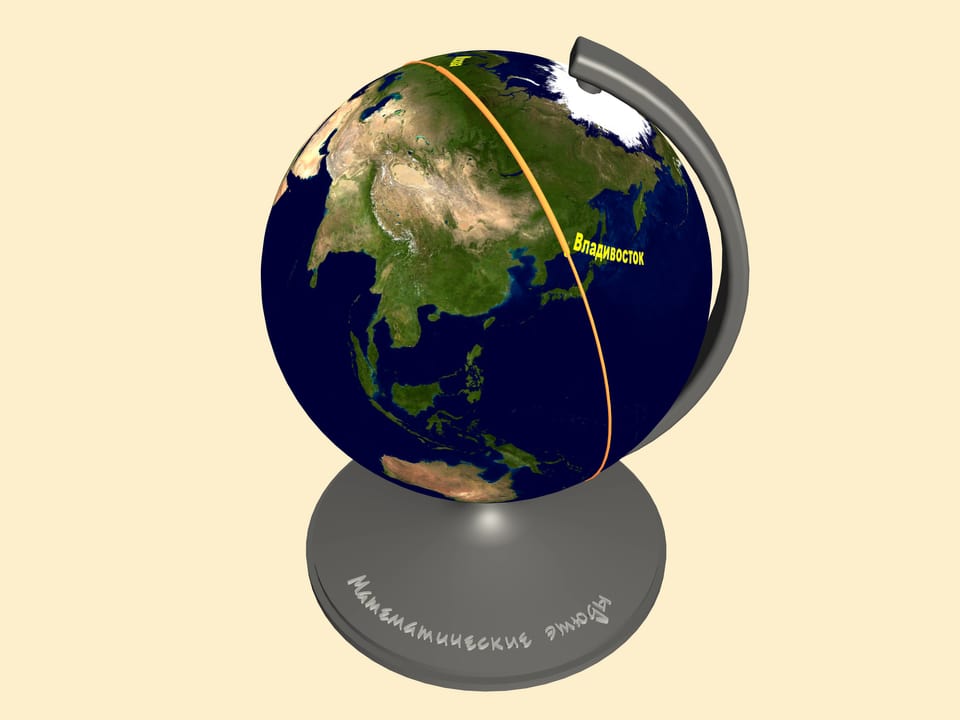
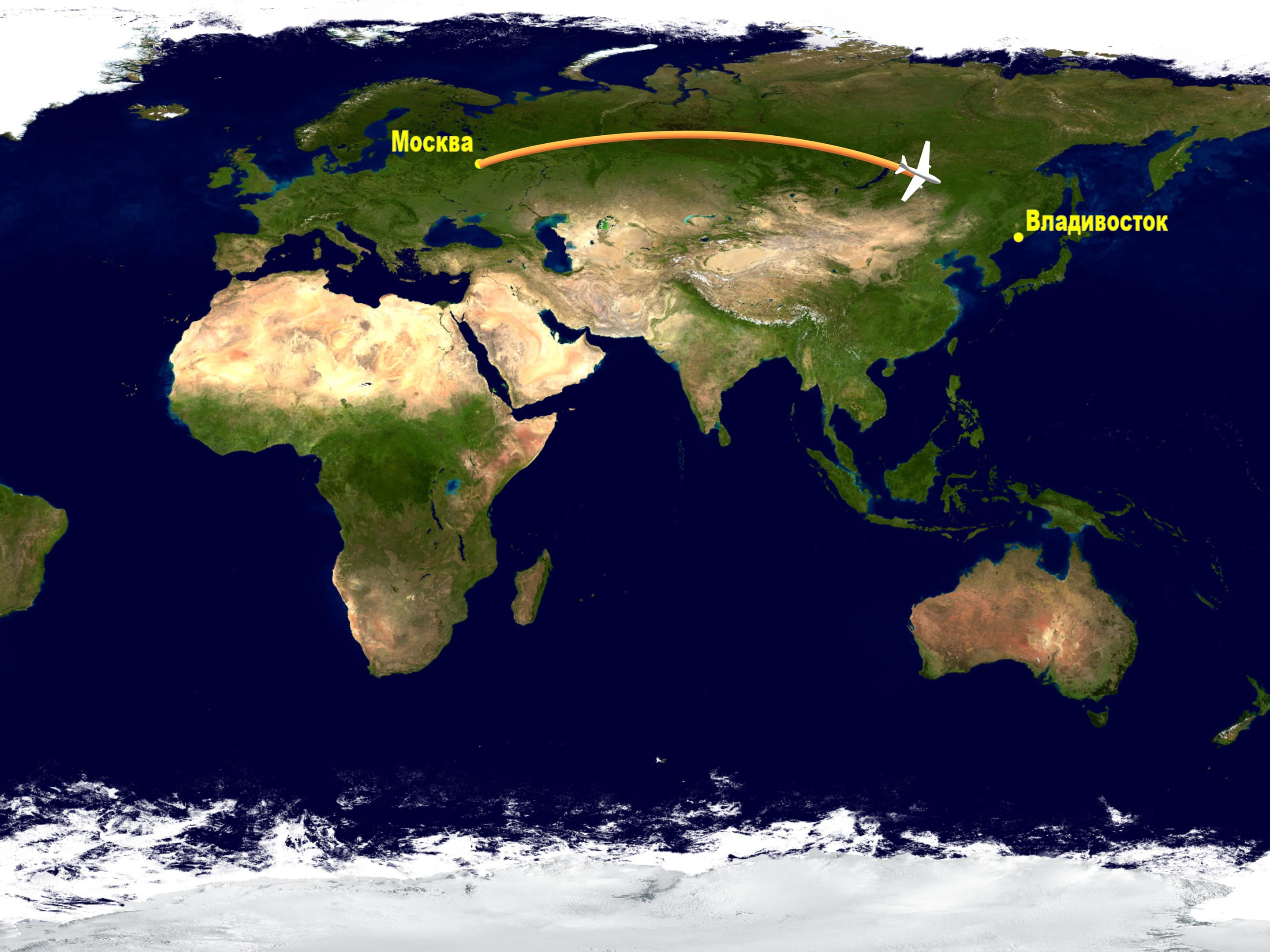
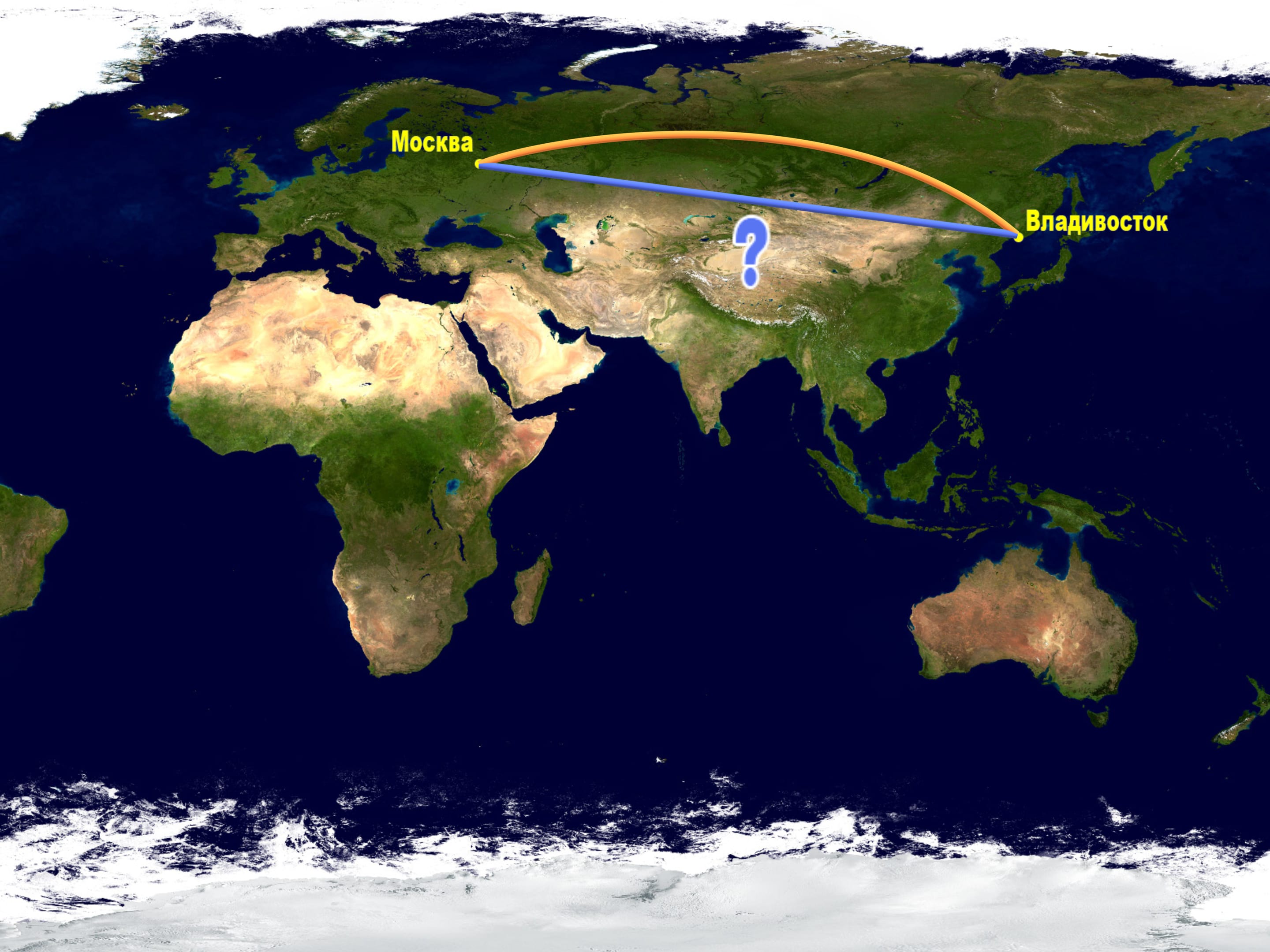
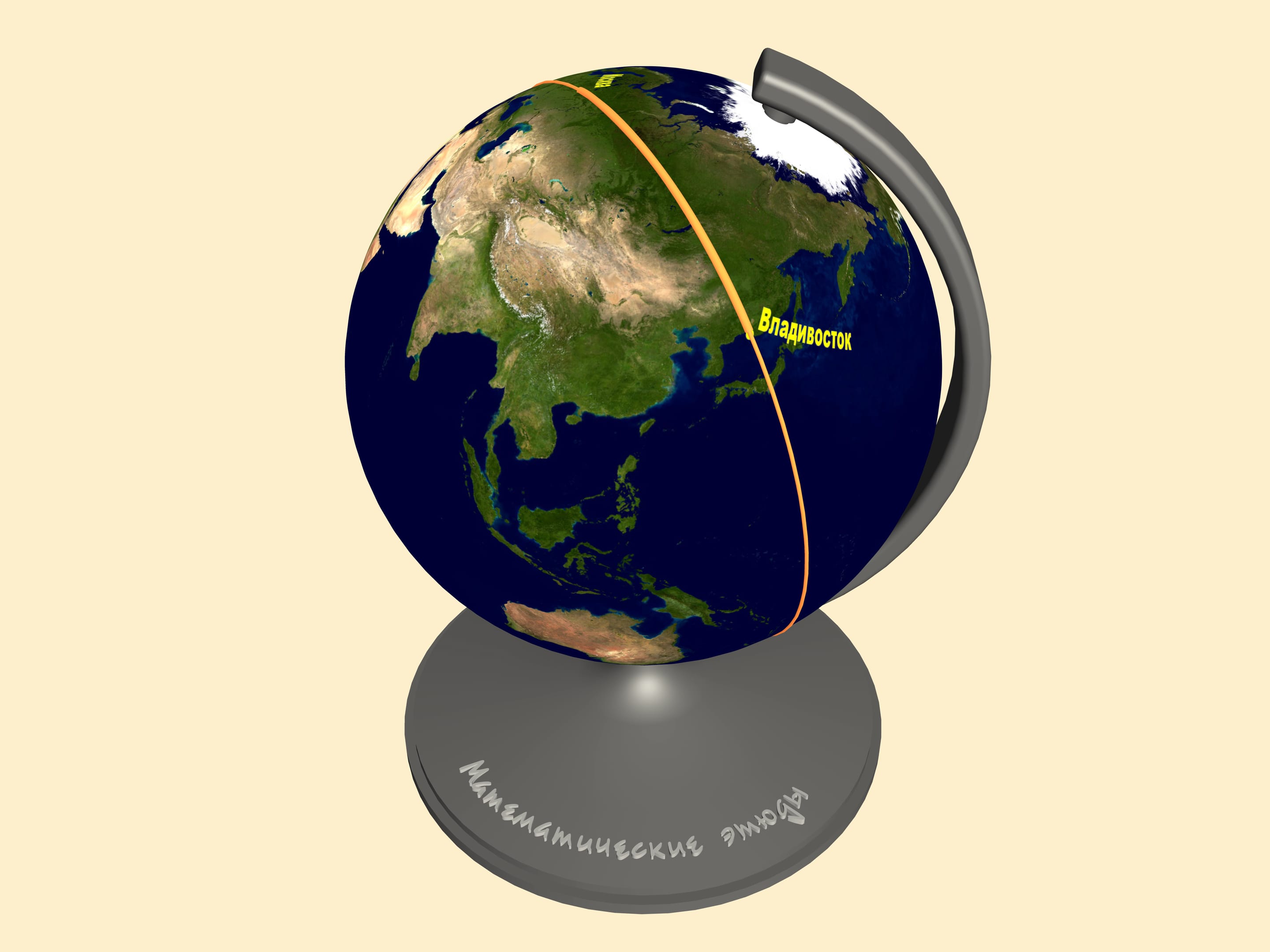
Let's look at a map created using one of standard projections and follow a trajectory the planes take from Moscow to the East of Russia, say, Vladivostok. If you have ever made this trip you might have noticed that the plane goes fare to the top of the map.
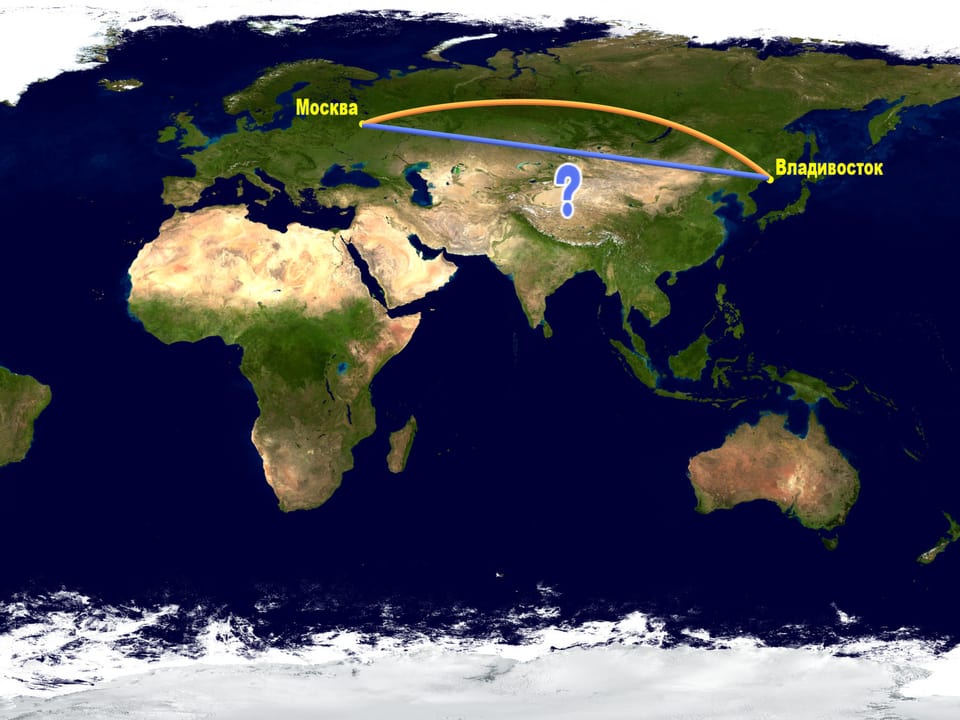
Well, a plane trip is an expensive one. Why do they make such a d’tour while one could go straight forward according to the map?
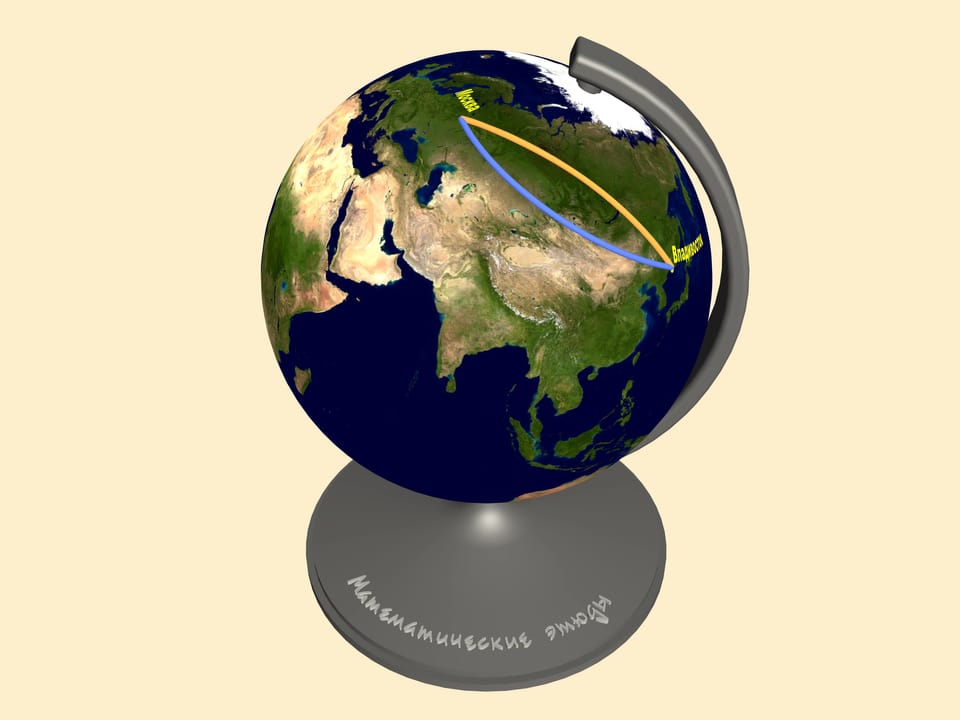
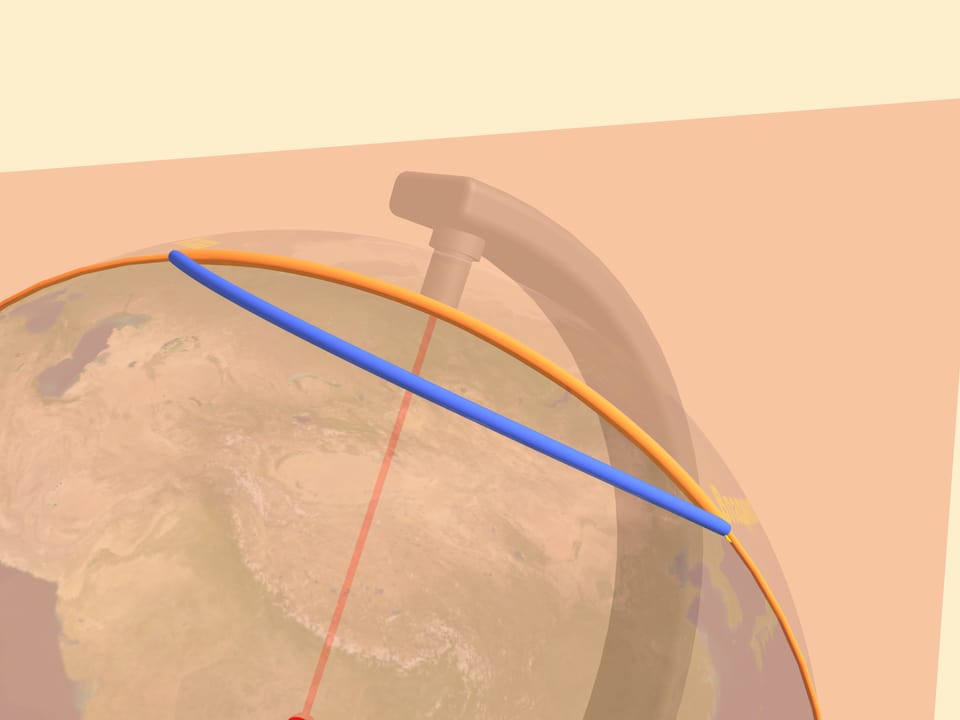
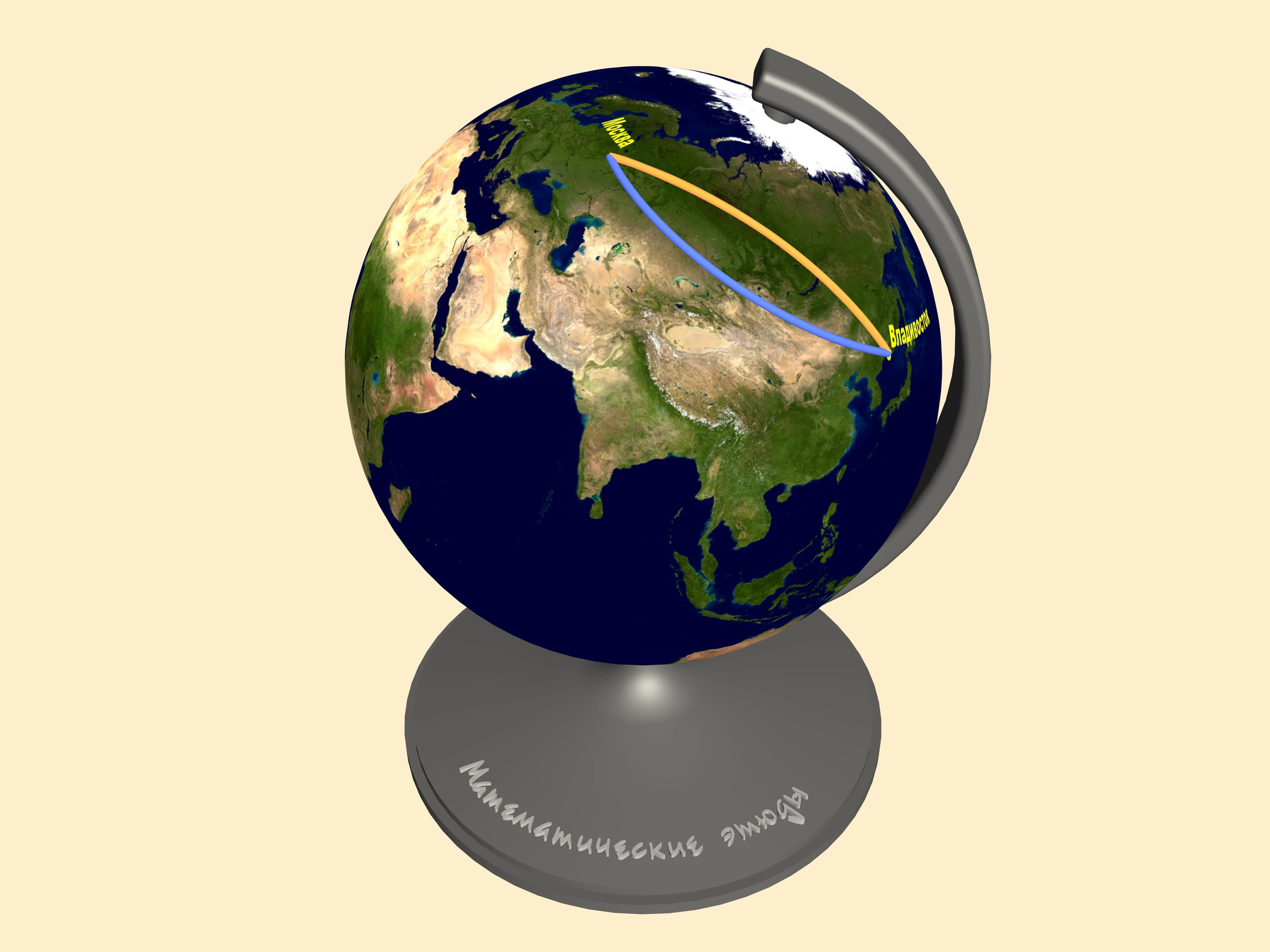
The answer is that the notion of the shortest path depends on the surface where it's measured. As we said before, every plane map represents the Earth surface with distortions. Consider the same trajectories on a globe. Only here we can judge the distance of our paths.
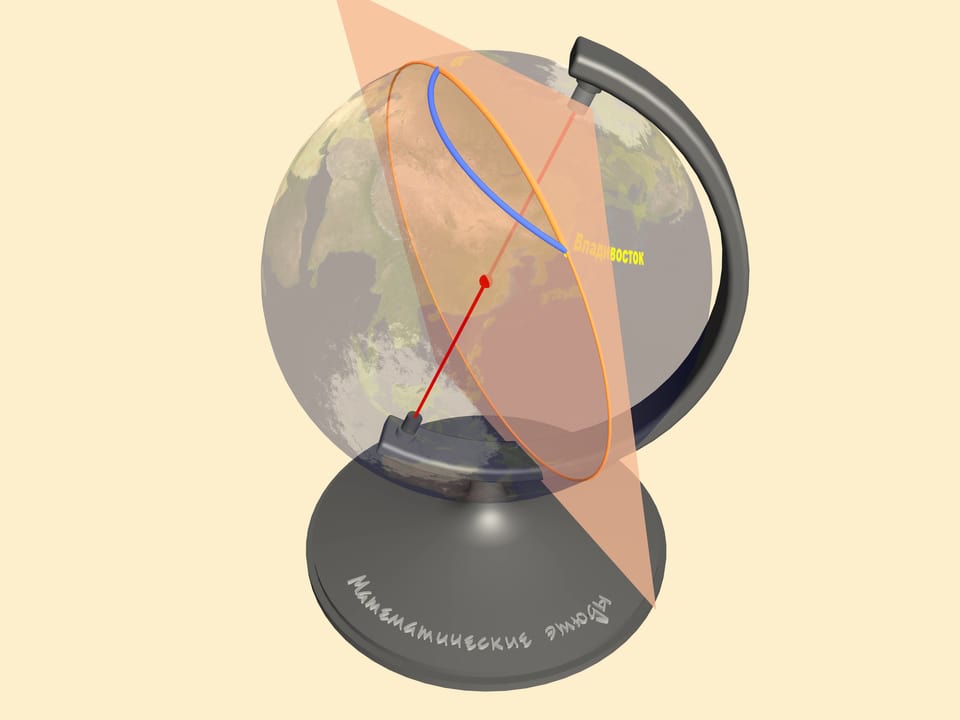
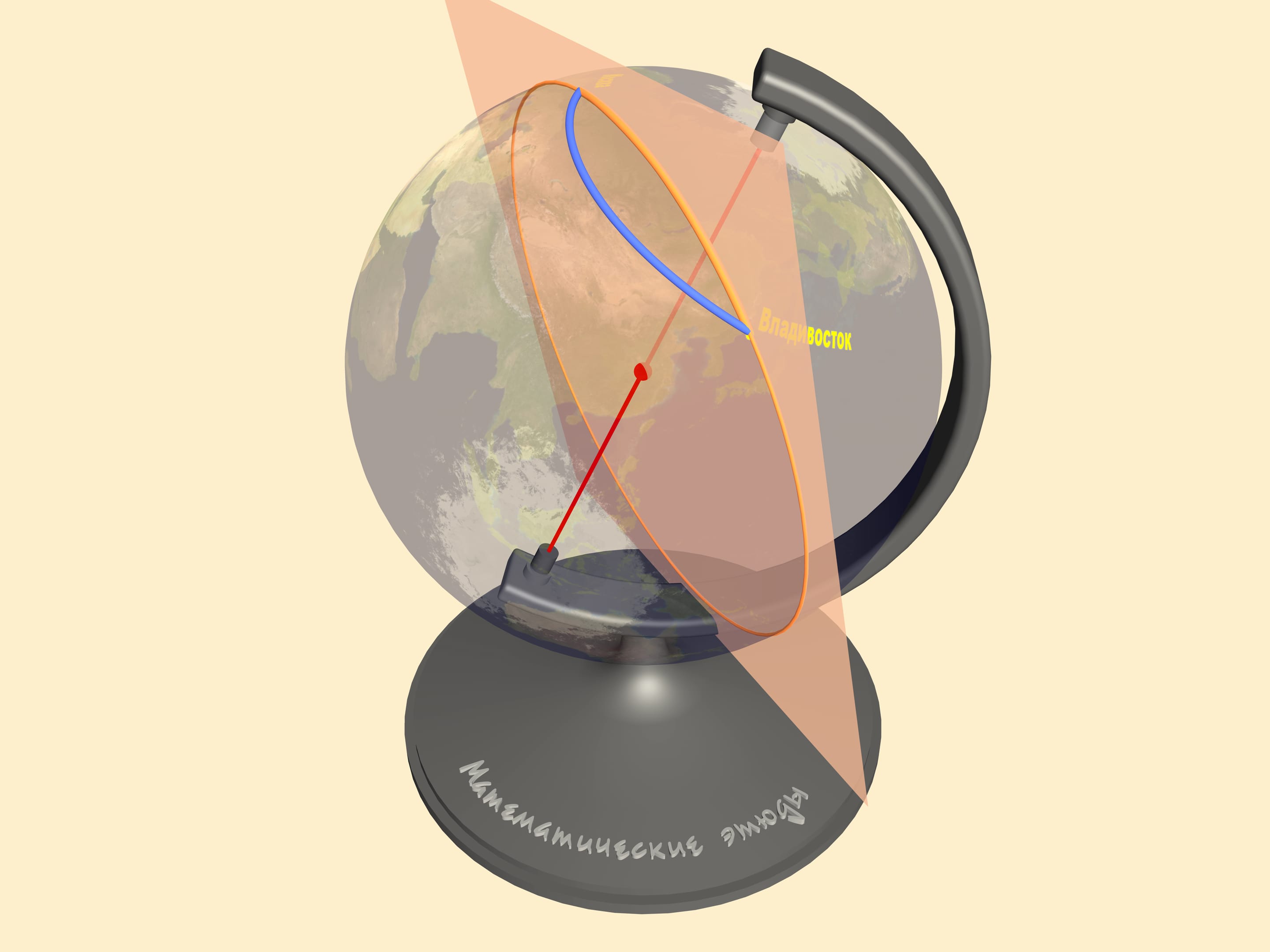
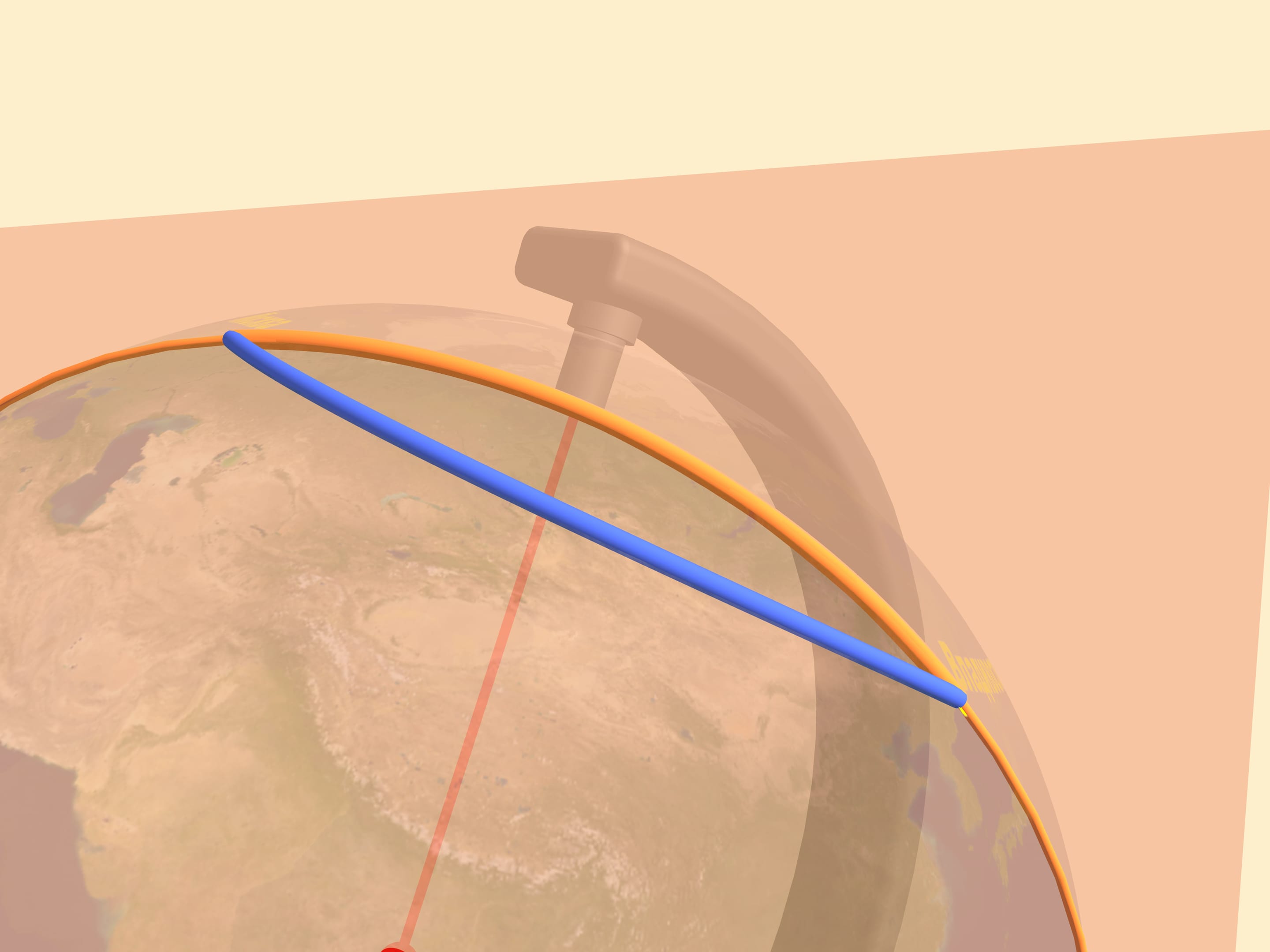
To find the shortest path between two points on a sphere one should draw a great circle containing them. This is a circle we get taking the section, of the sphere and the plane containing our points and the sphere's center. The shortest of the two arcs of the great circle, connecting the points is the shortest path between them. In mathematics such a curve is called a geodesic on the given surface.
All the other trajectories on the map, including the straight line, turn out to be longer than the arc!
As we've seen, the planes use exactly the great arc, i.e. the shortest path.