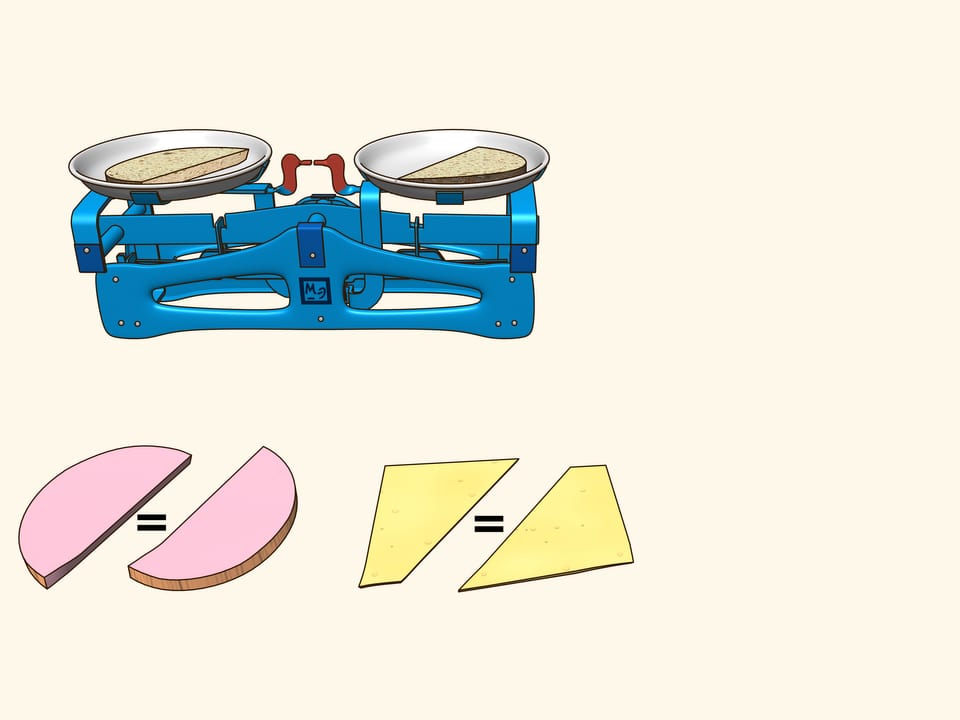
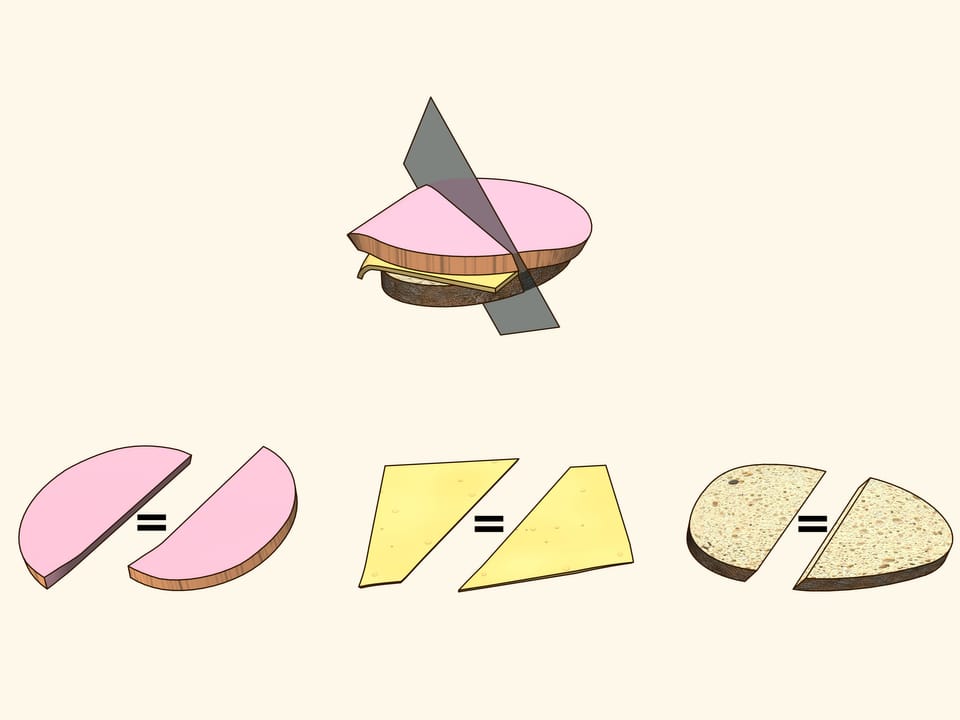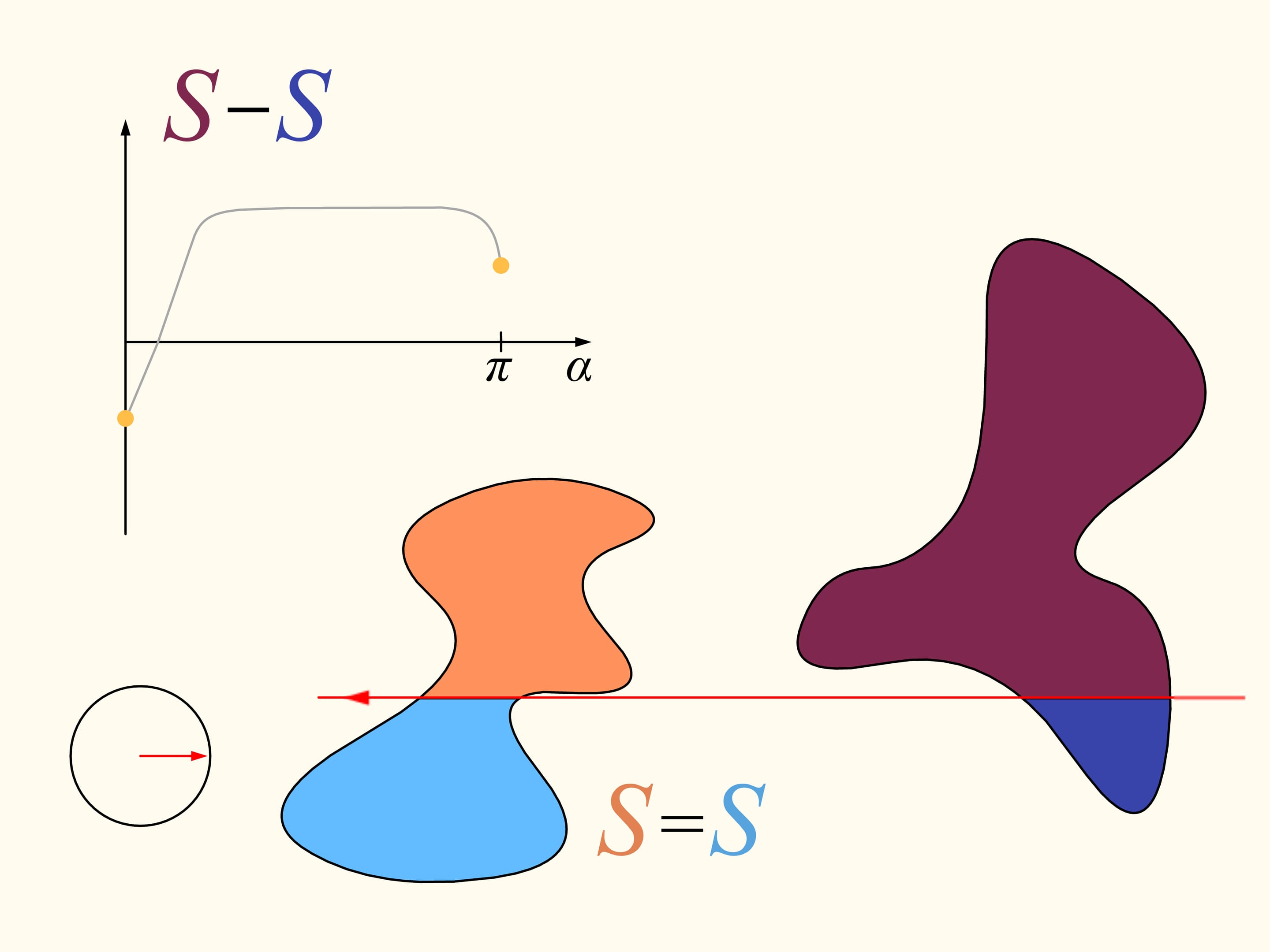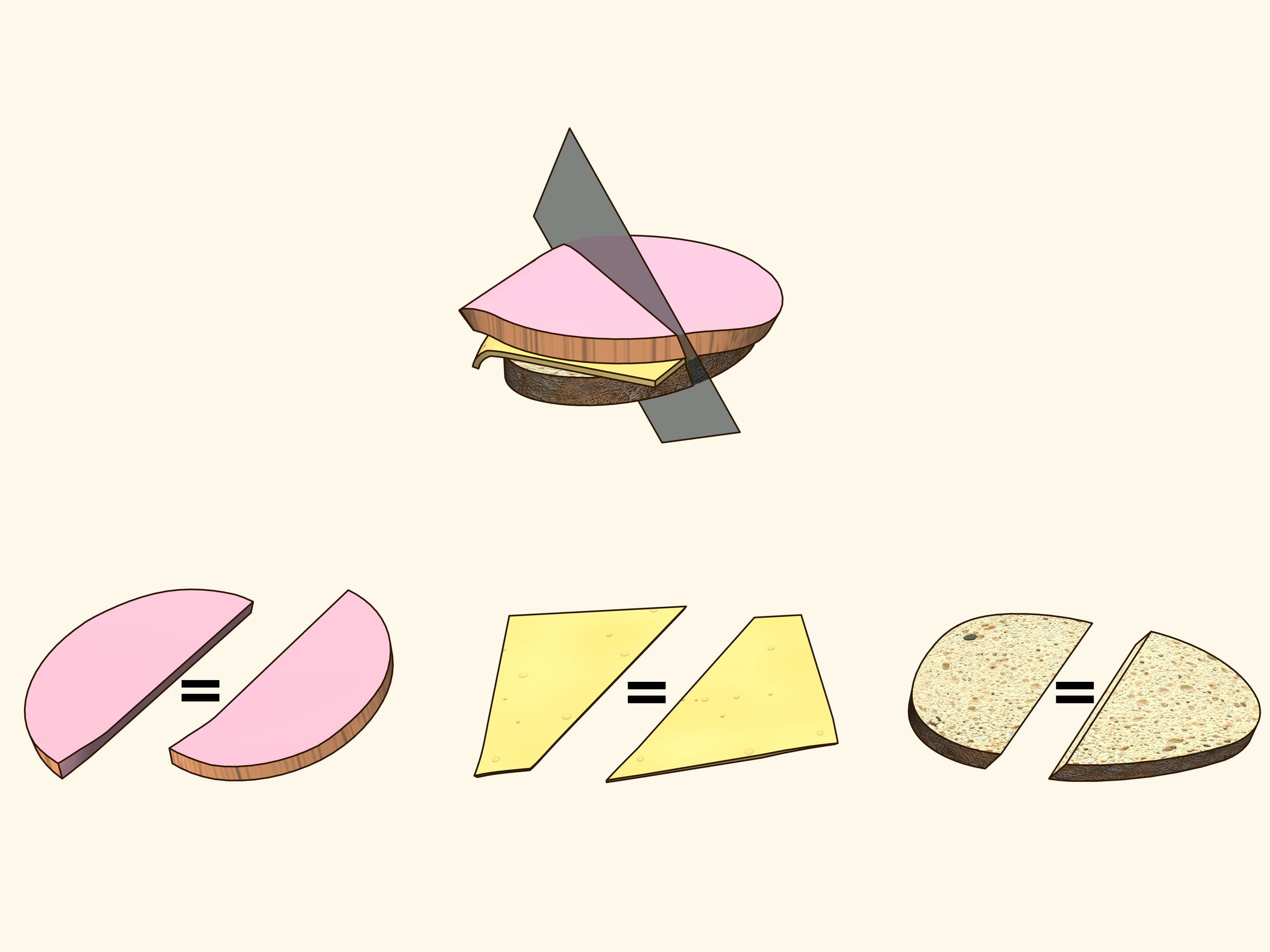Can you cut by a planar section a sandwich consisting of a slice of bread, a slice of cheese and a slice of ham in such a way that both sides contain the same amounts of bread, cheese and ham? We will show that you can...
Consider first the two-dimensional problem. Suppose we are given any two regions in the plane. Does id exists a straight line that simultaneously bisects the first region and the second one in two parts with exactly the same area?
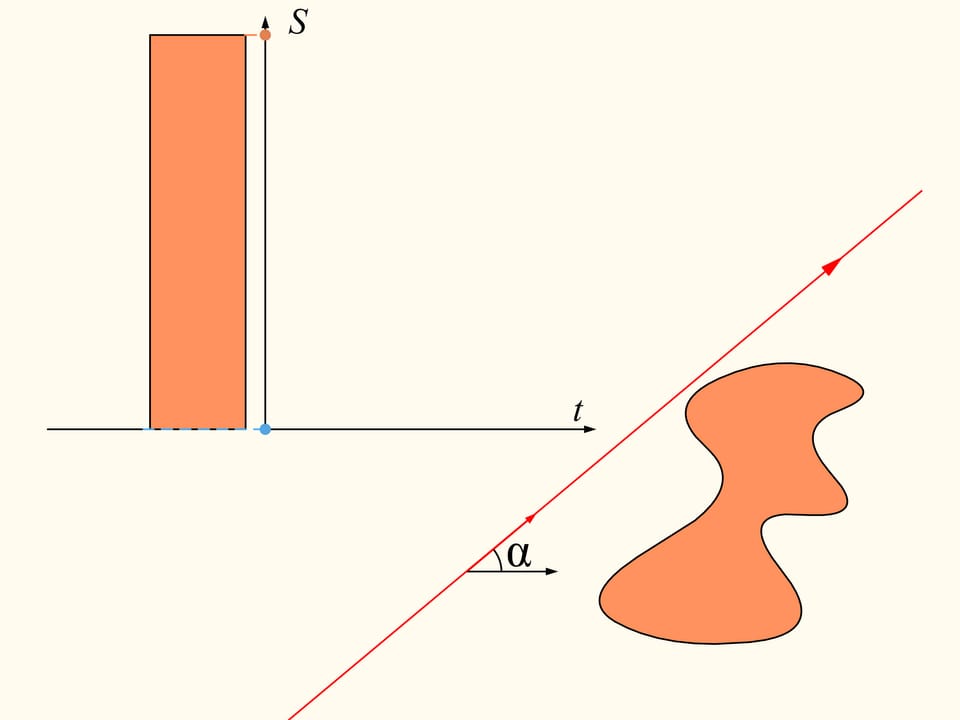
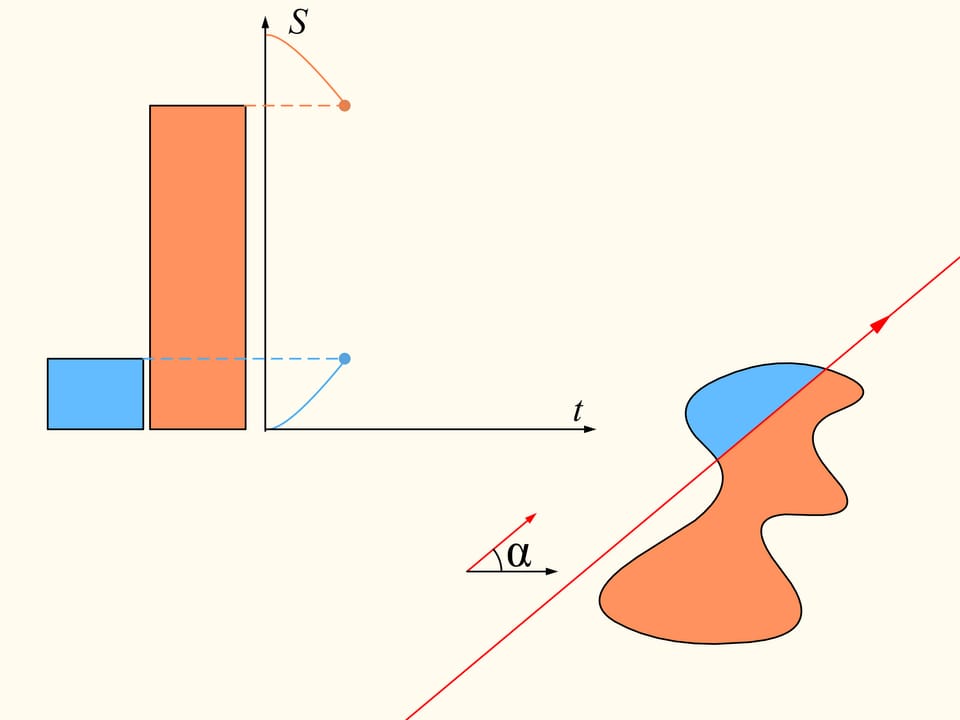
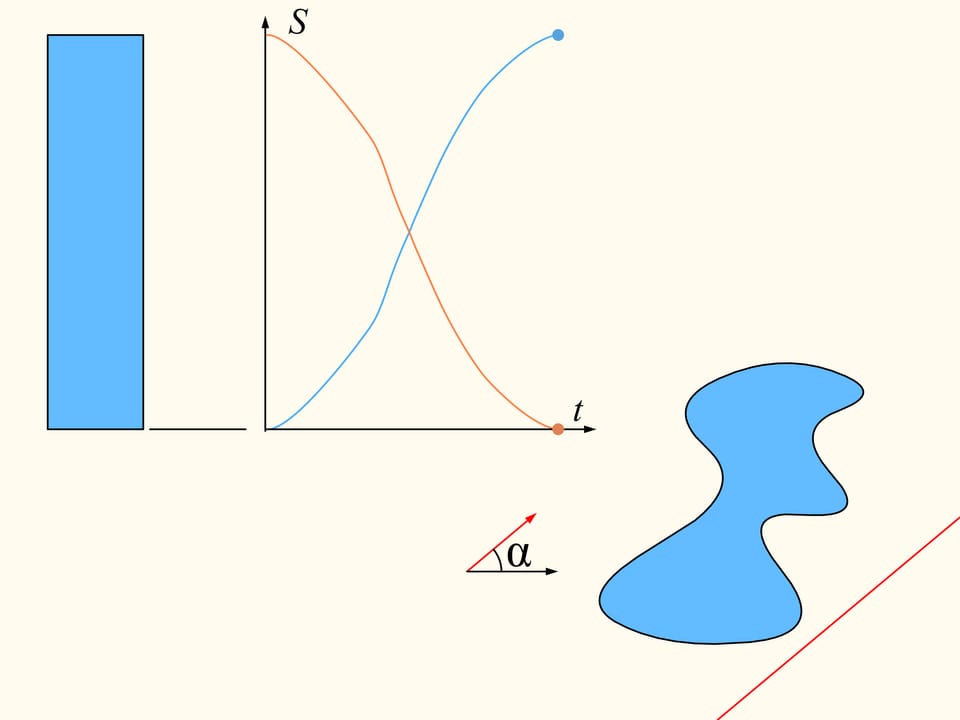
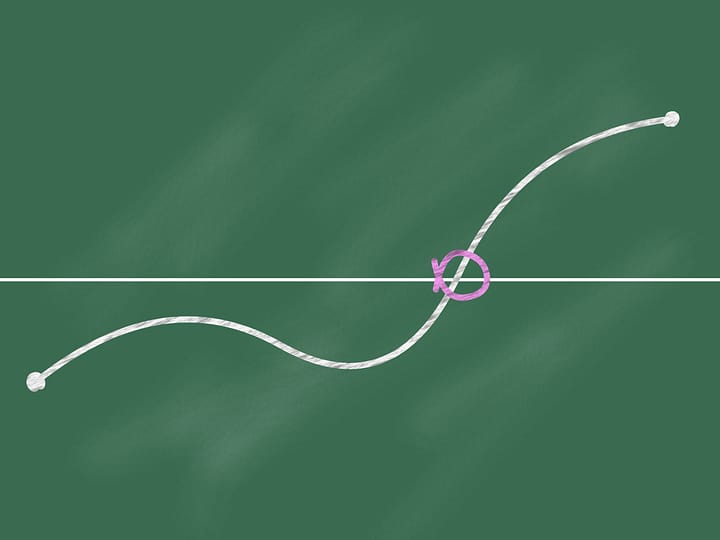
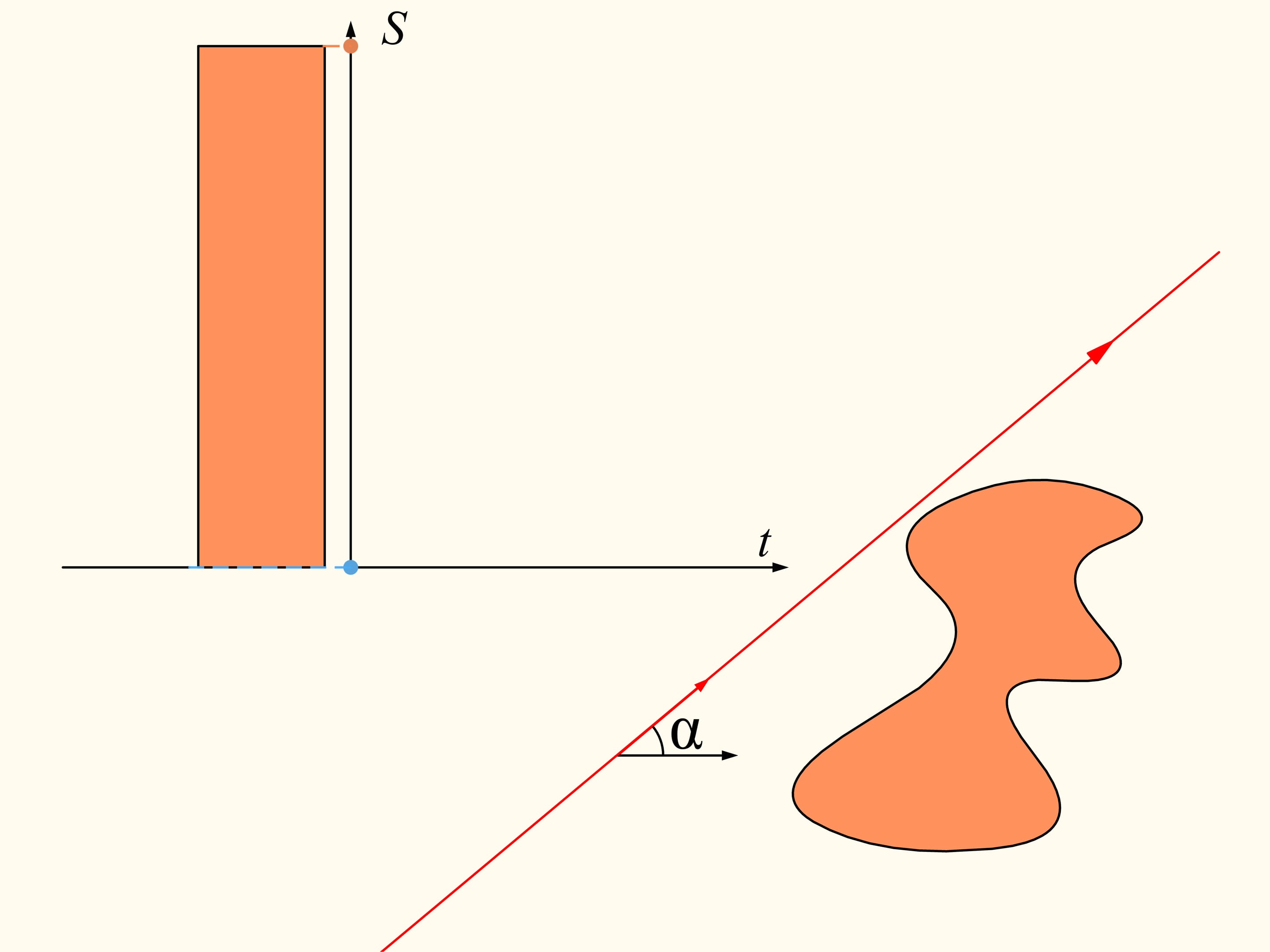
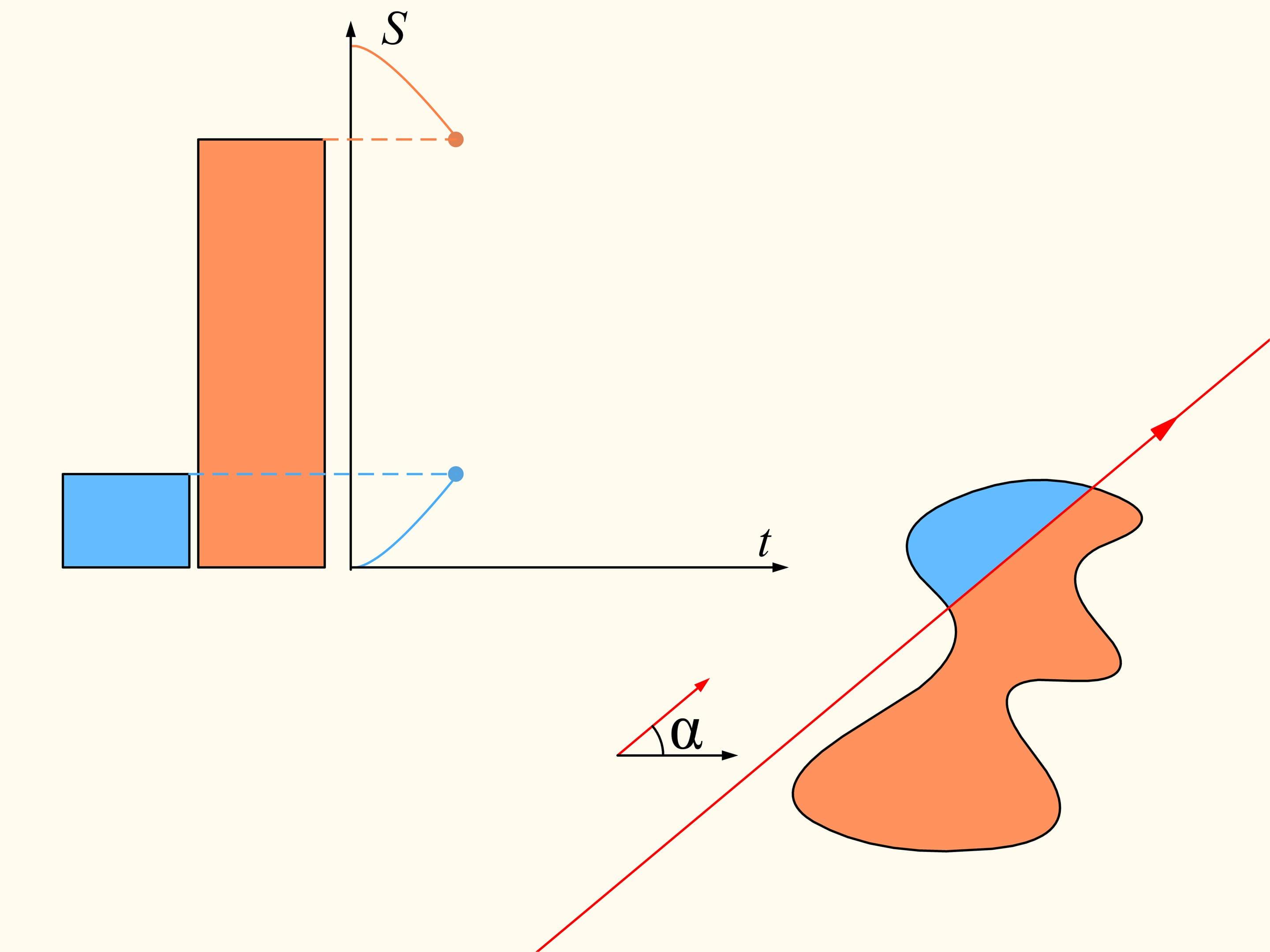
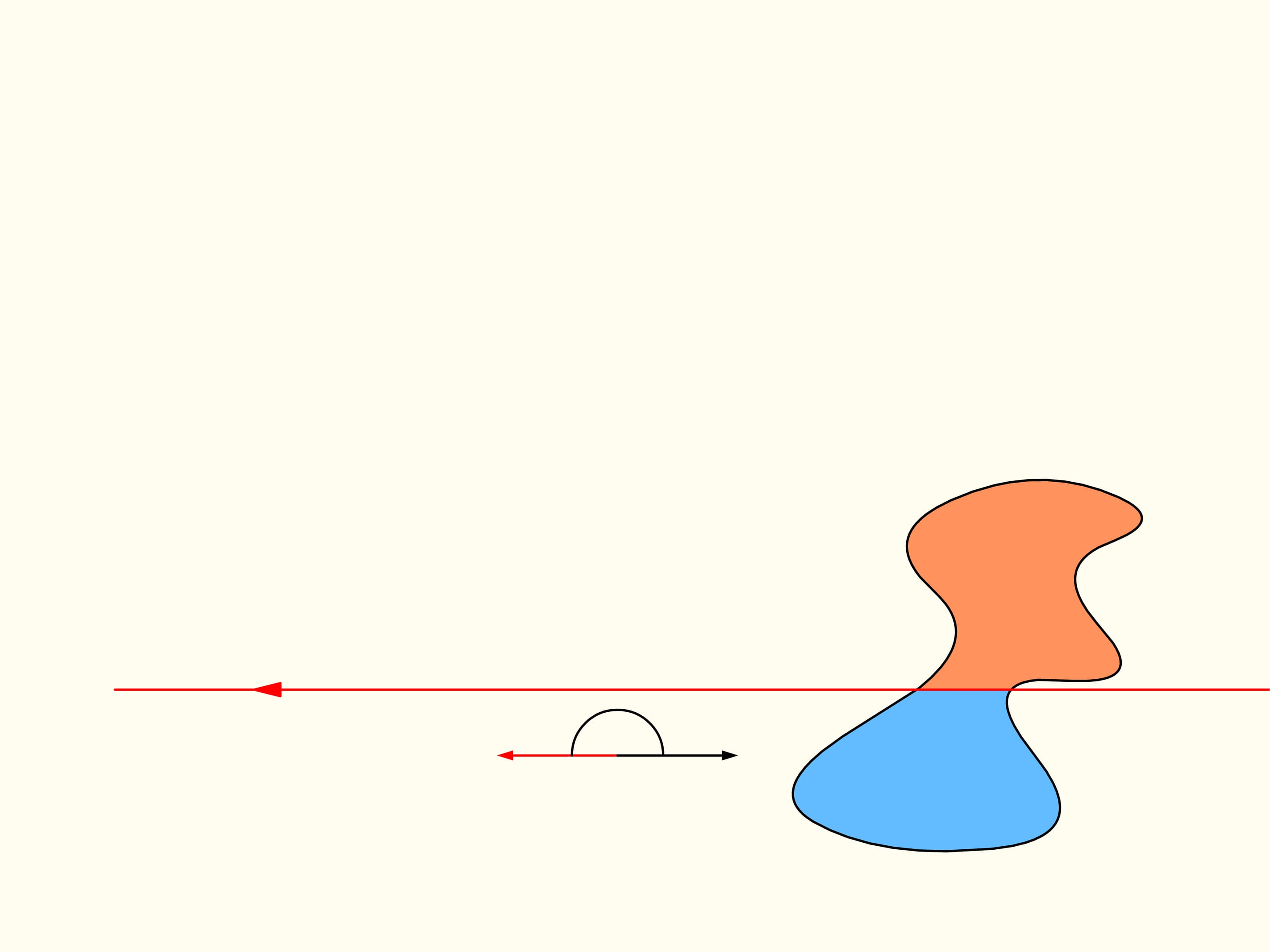
To demonstrate that it exists, let’s initially consider only one of the regions. We choose an arbitrary direction. Is there a line with this direction that divides the region into two parts of equal area? We show that this line exists any direction is chosen. Take the straight line with the chosen direction far from the region so that the region is completely on the same side with respect to it, for instance on the right side. We will build two graphs, representing the areas of the region that are located on the right and on the left of the line, as functions of the distance of the straight line from its initial position. At first the whole region is on the right of the line, which means that the left element of the histogram is zero whereas the right element represents the entire area of the region. We start to move the line to the right so that it is always parallel to its initial position. During this shift the area of the region located to the right of the line will decrease continuously, while the area to the left will increase continuously. At the end, the whole region will be on the left of the line. The left part of the histogram (in blue) then represents the area of the entire region, and the right one will be zero.
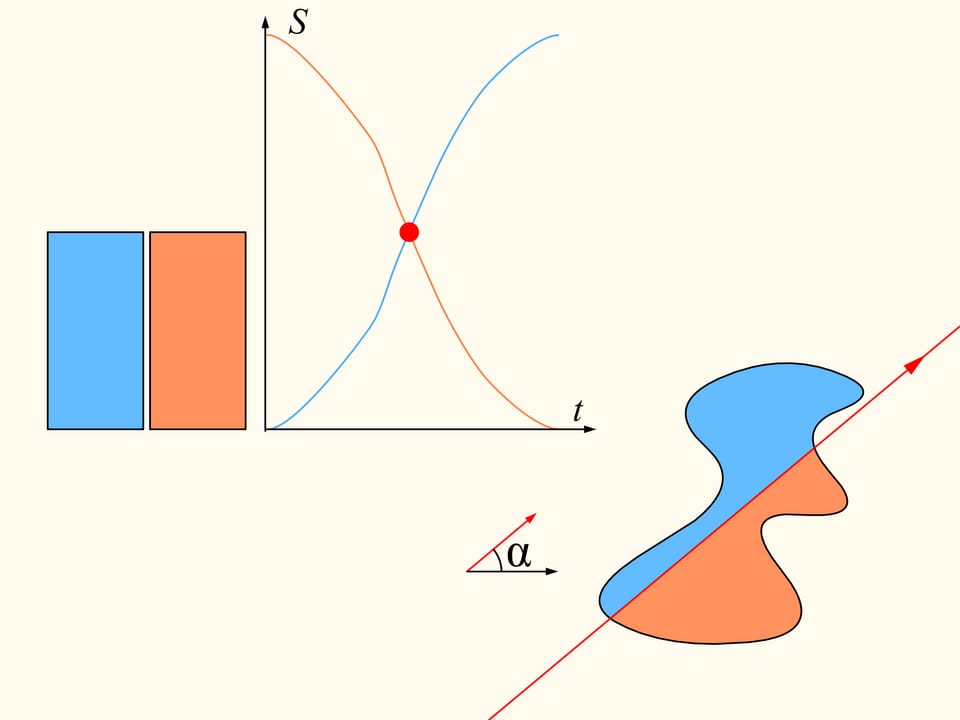
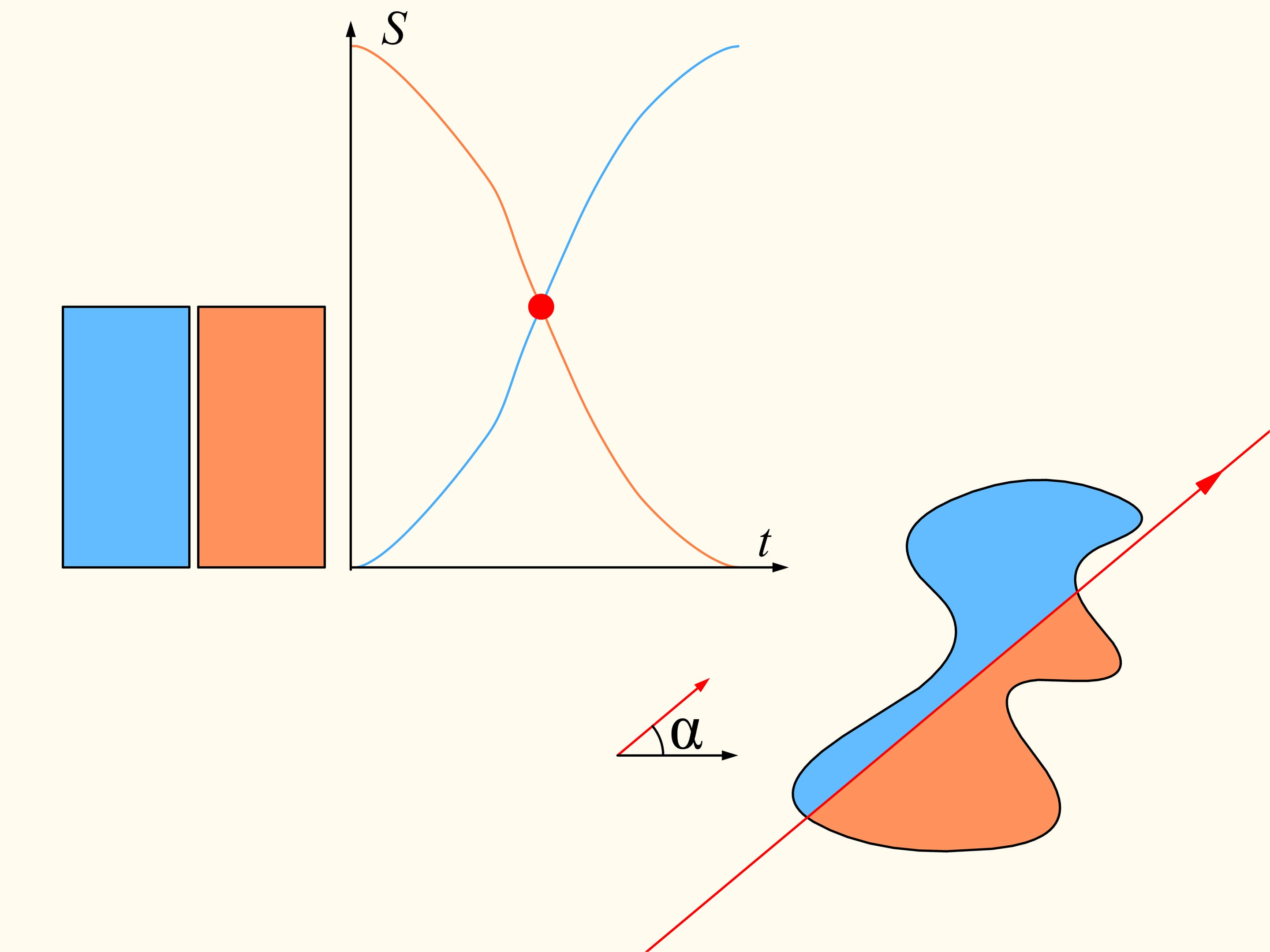
If we look at the graphs representing the areas at left and at right of the line as functions on the distance of the line from its initial position, we will see that they have somewhere a point of intersection, precisely because of their continuity. This point tell us exactly the location of the line that divides the area of the region into two equal parts.
Since the direction of the line was chosen arbitrarily, a line that divides the region into two equal parts exists in any direction.
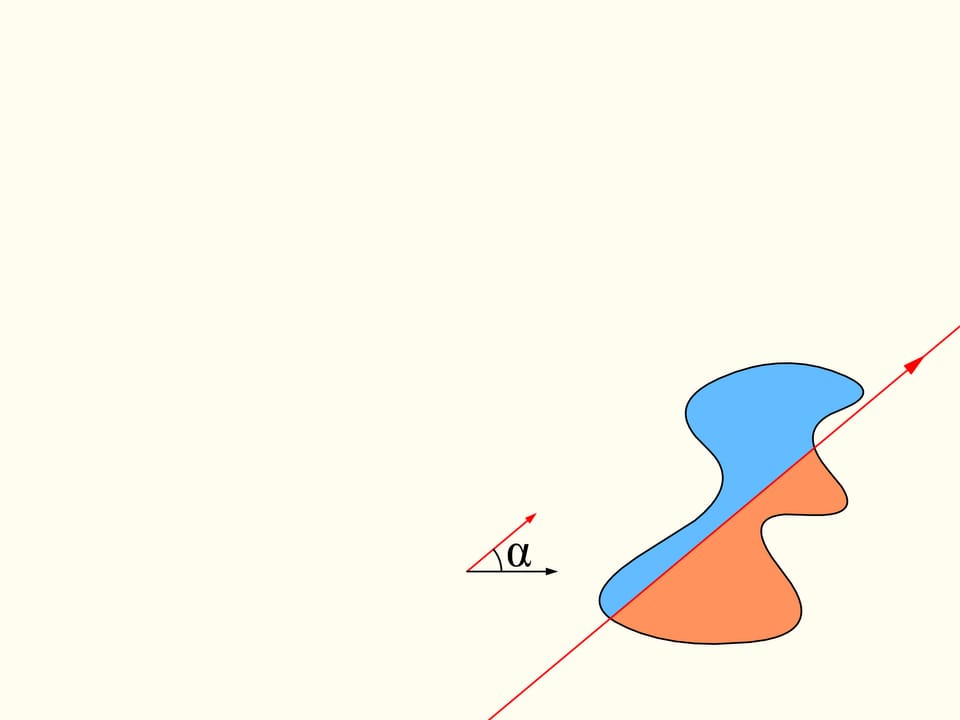
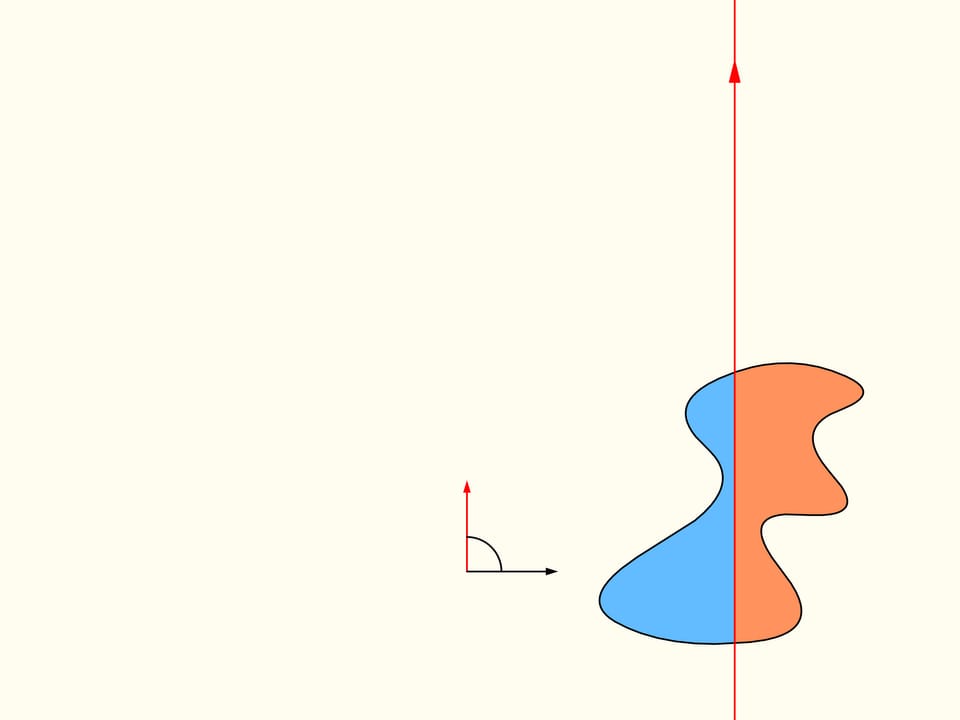
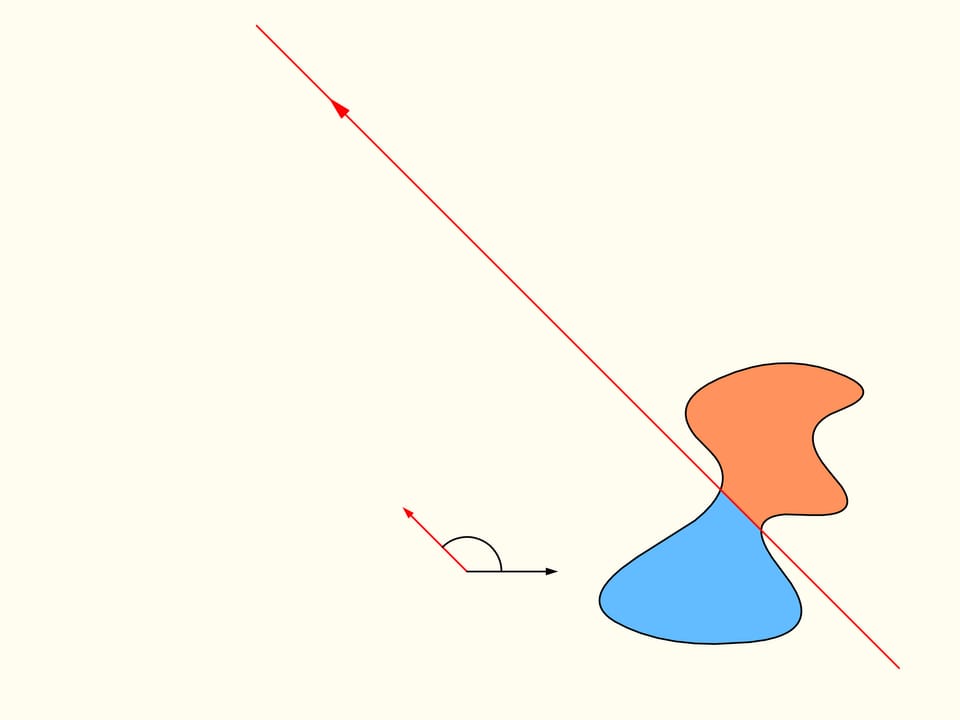
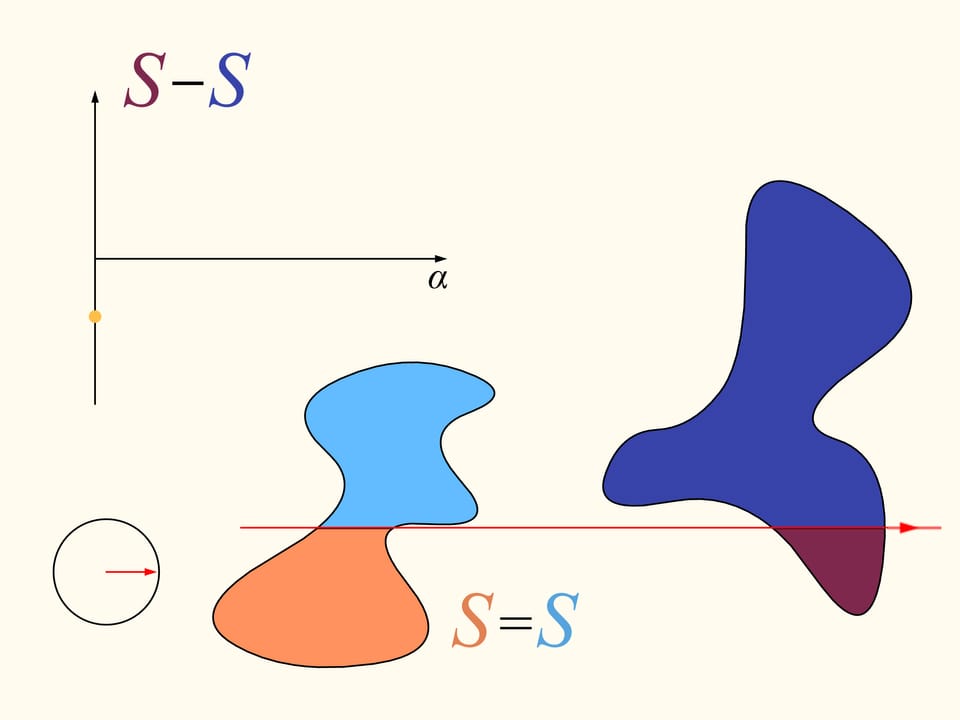
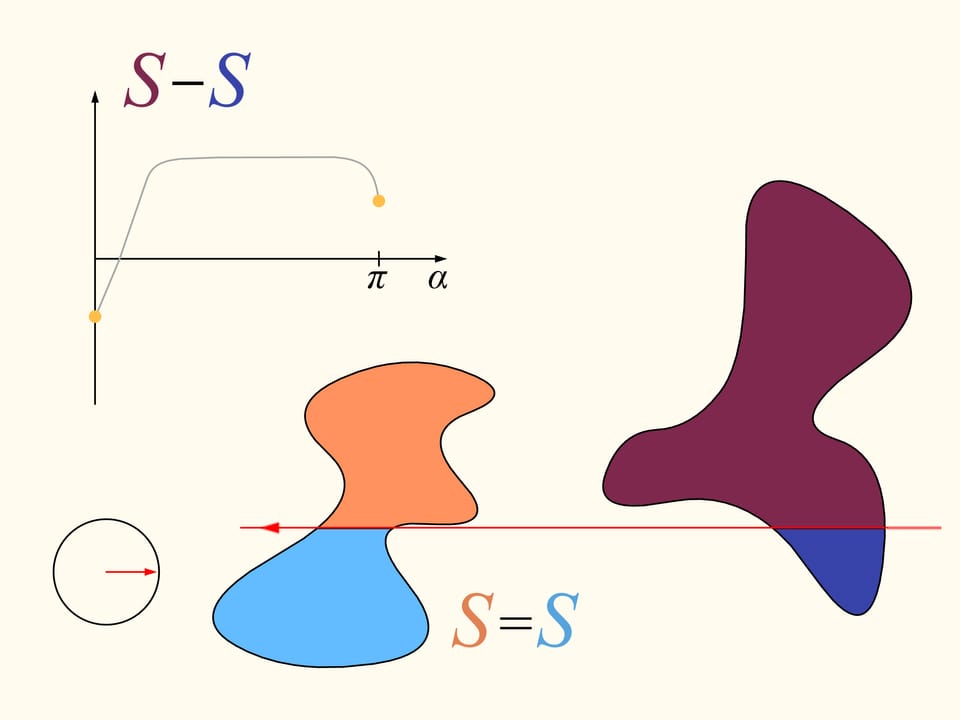
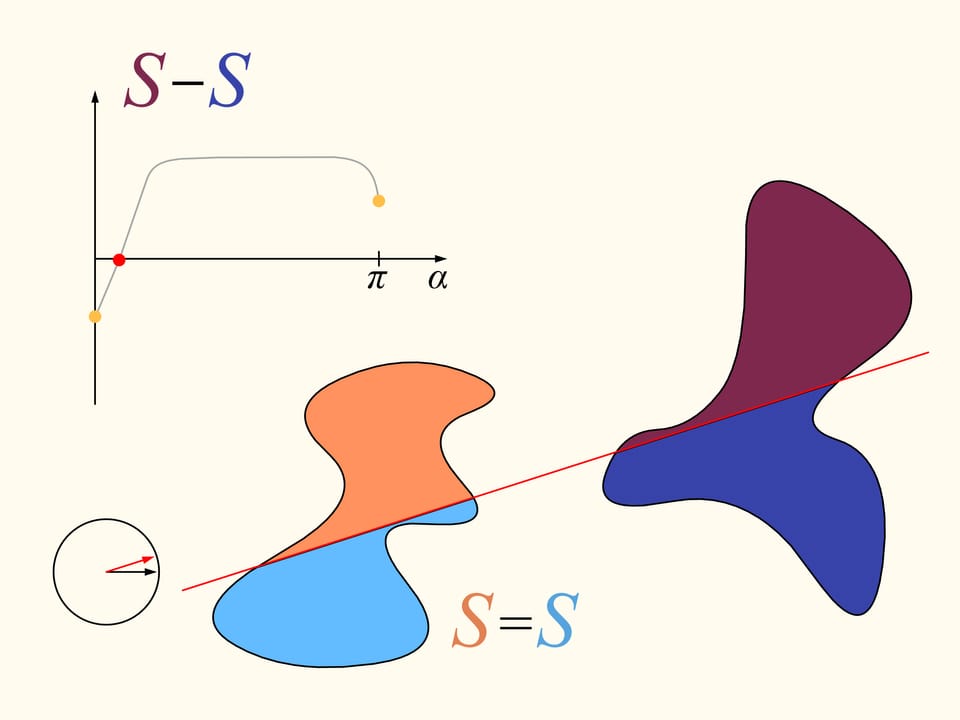
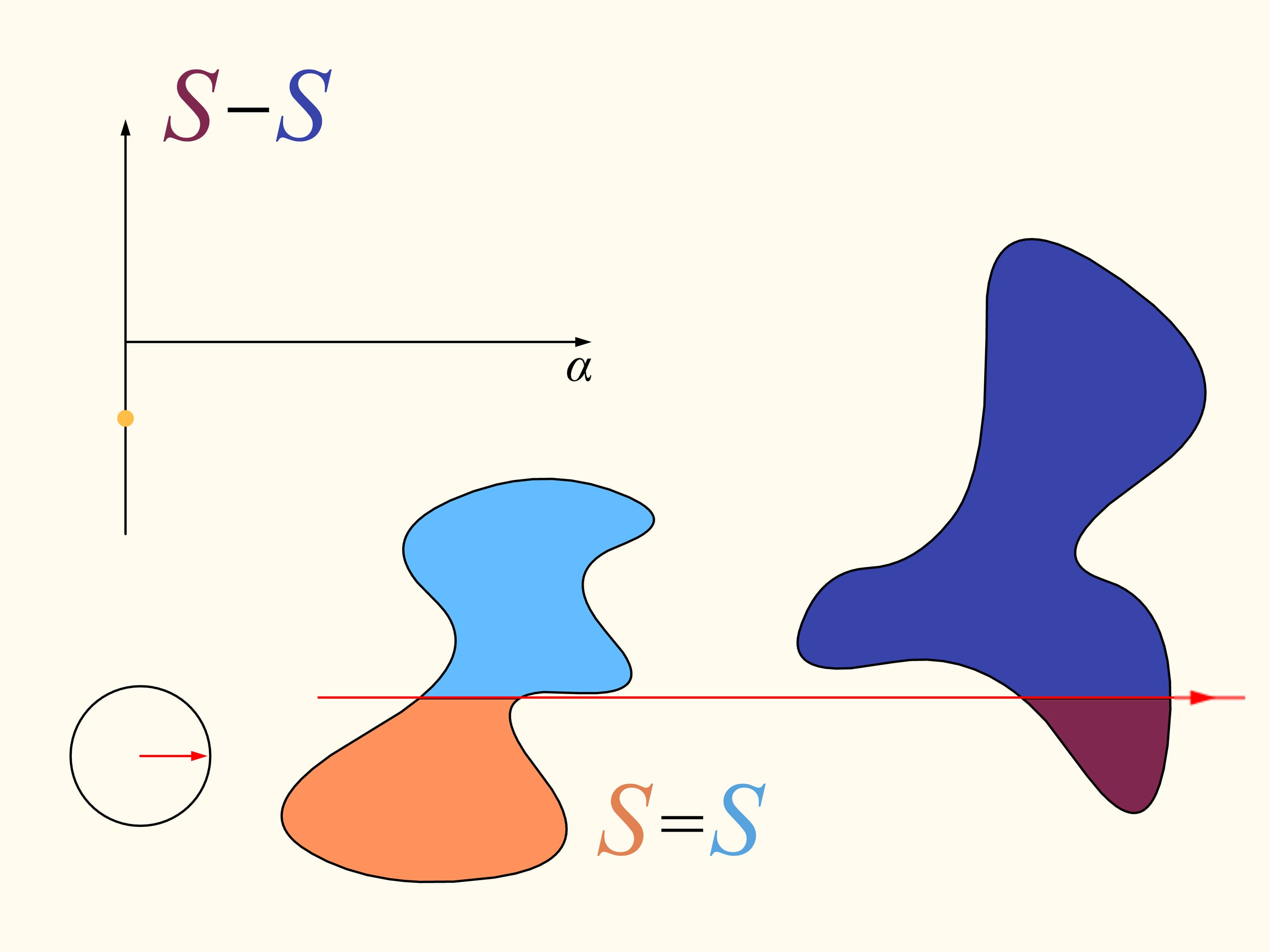
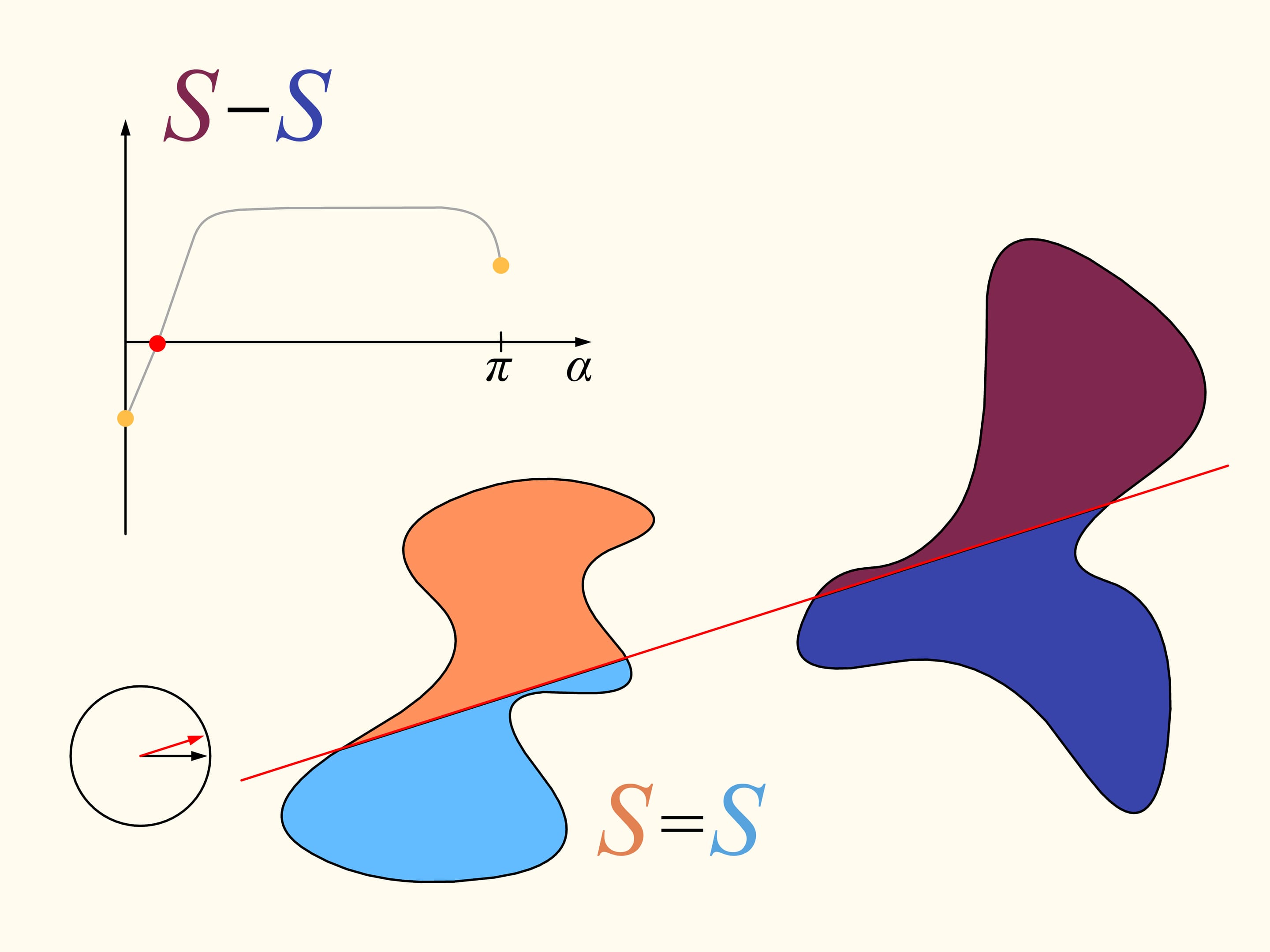
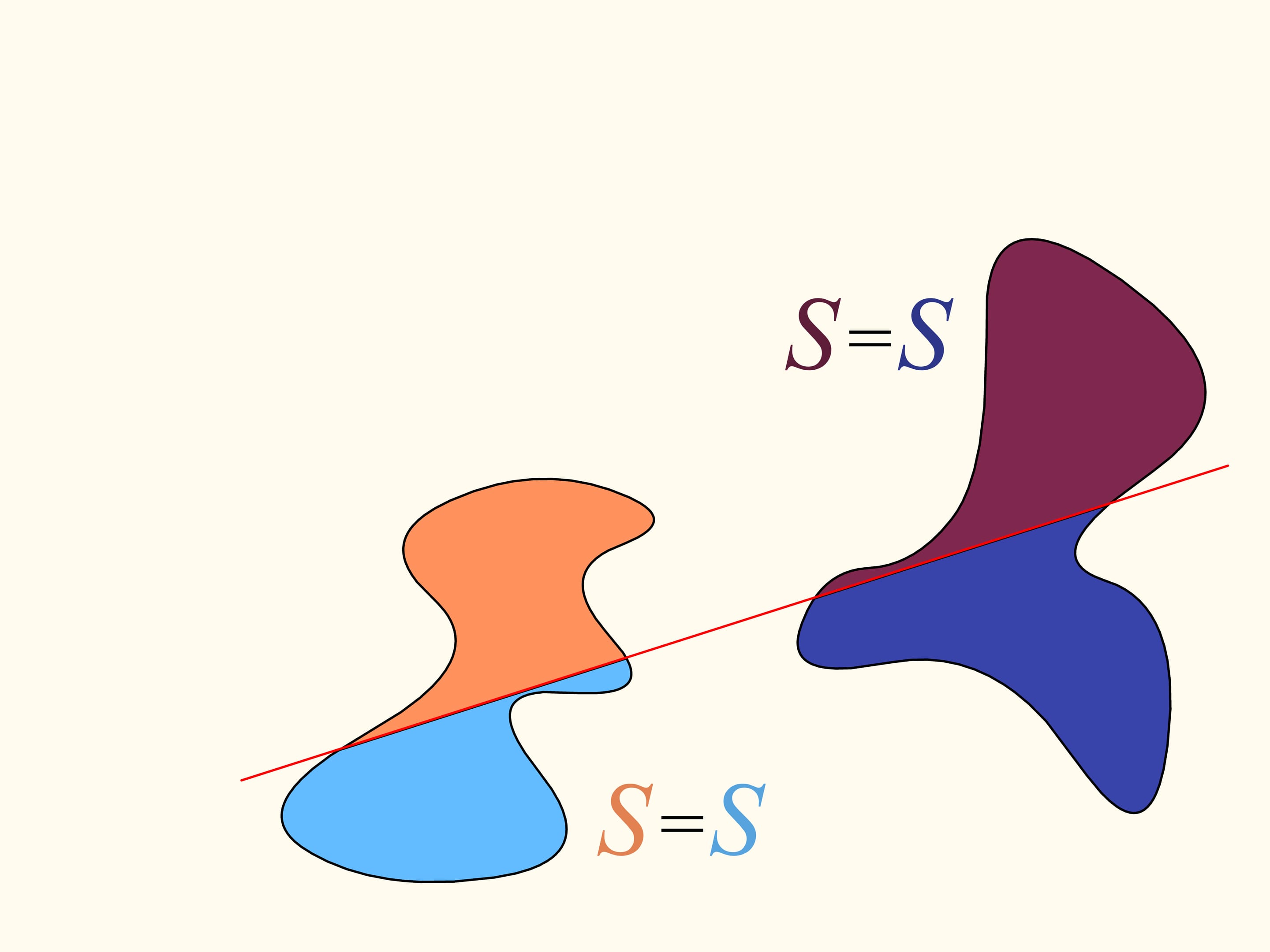
Let us come back to the case of two regions. We will consider only those straight lines that cut the first region (on the left) into two equal parts, and we start choosing the line that is horizontal and points to the right. It will cut the second region (on the right) in some way. Now we change the direction of the line, remaining inside the set of straight lines that bisect the first region. We construct the graph of the difference of areas of the first region located at the left and at the right of the line, depending on the angle made by the line with the initial one, which is horizontal. Initially this difference is negative. Continuously changing the direction of the line we will return to the starting position, but inverted, so that the areas at left and at right are exchanged. At this moment the value of the difference will be positive. Since the difference changes continuously, its graph, going from a negative to a positive value must meet the line of the zero value. This value corresponds to an angle that determines the line that divides the second region into two parts of equal areas. In this way we have found the straight line which divides both regions into two parts of equal areas.
Here is how the Bolzano-Cauchy theorem is used. Unfortunately, how to draw this line when we are given two regions of arbitrary forms, arbitrarily arranged in the plane, we cannot know without using other ideas and knowledge. But it exists, for any pair of regions! The theorems of this type are called “theorems of existence.”
Let us now return to the three-dimensional case. Instead of two regions in the two-dimensional plane we will consider three arbitrary objects, arbitrarily arranged in the space. Instead of the areas, we will consider the volumes, and instead of a straight line, a plane. It happens that in this case, by an argument similar to that used in the planar case, we can prove a theorem of existence. For any three objects there is a plane that divides simultaneously each of them into two parts of equal volume.
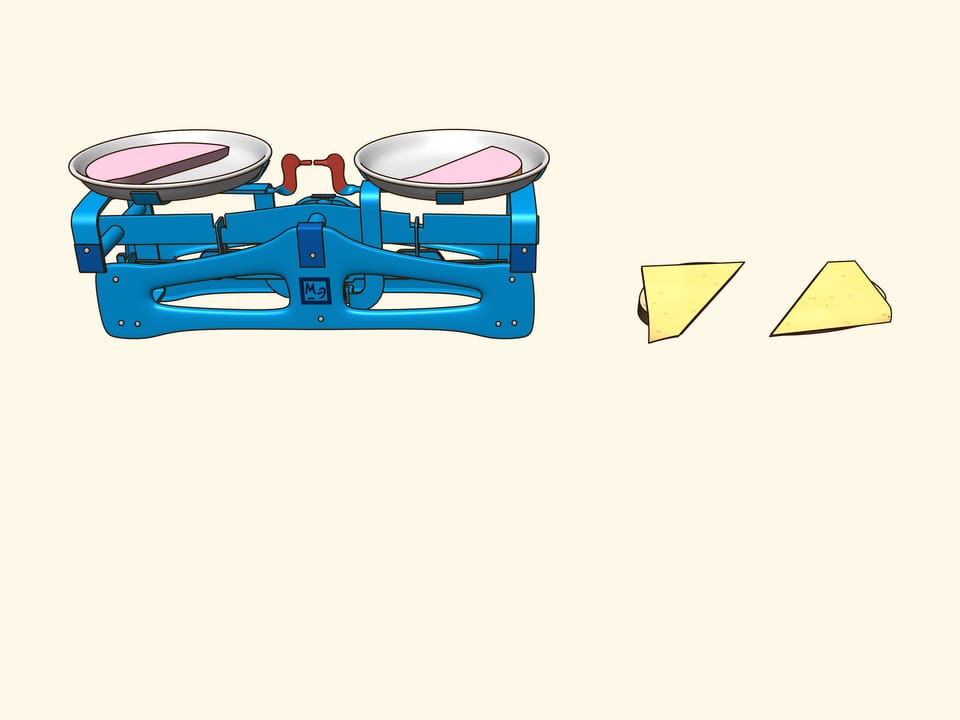
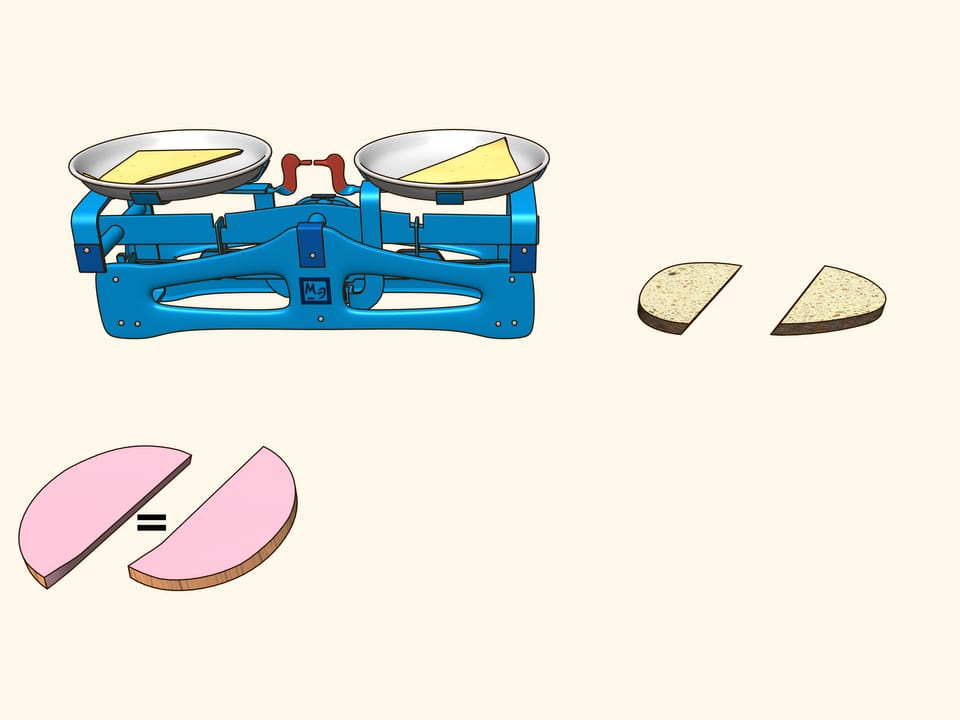
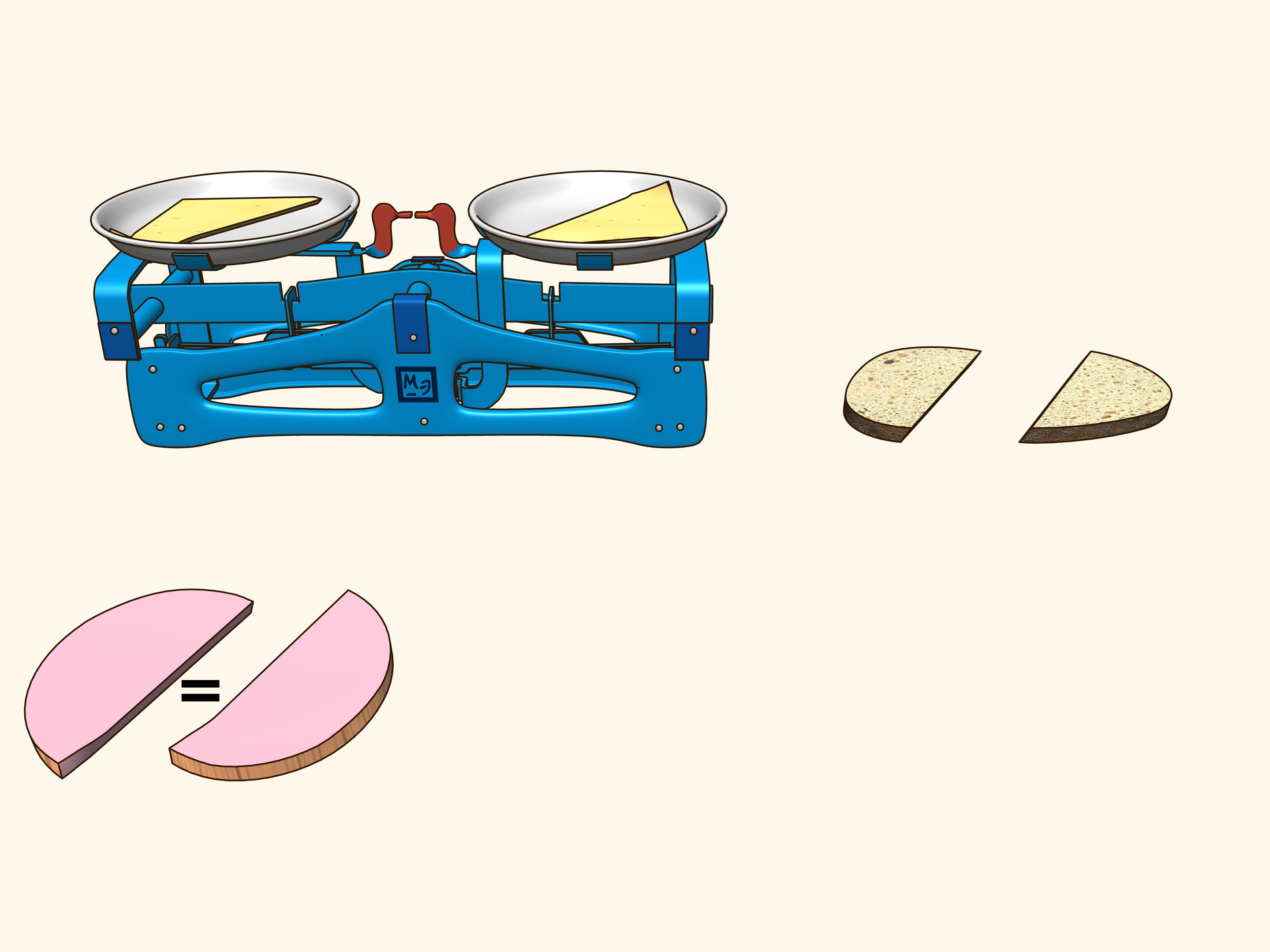
In order life have more flavour, consider a sandwich made of bread, cheese and ham. They are three objects arranged in some way with respect to each other. Try to show that there is a plane that cuts the ham into equal parts and simultaneously cuts the cheese and the bread in equal parts. Using additional arguments, this plane was found for the sandwich shown in the film, and indeed it is evident from the verification that all three objects were divided into two equal parts!