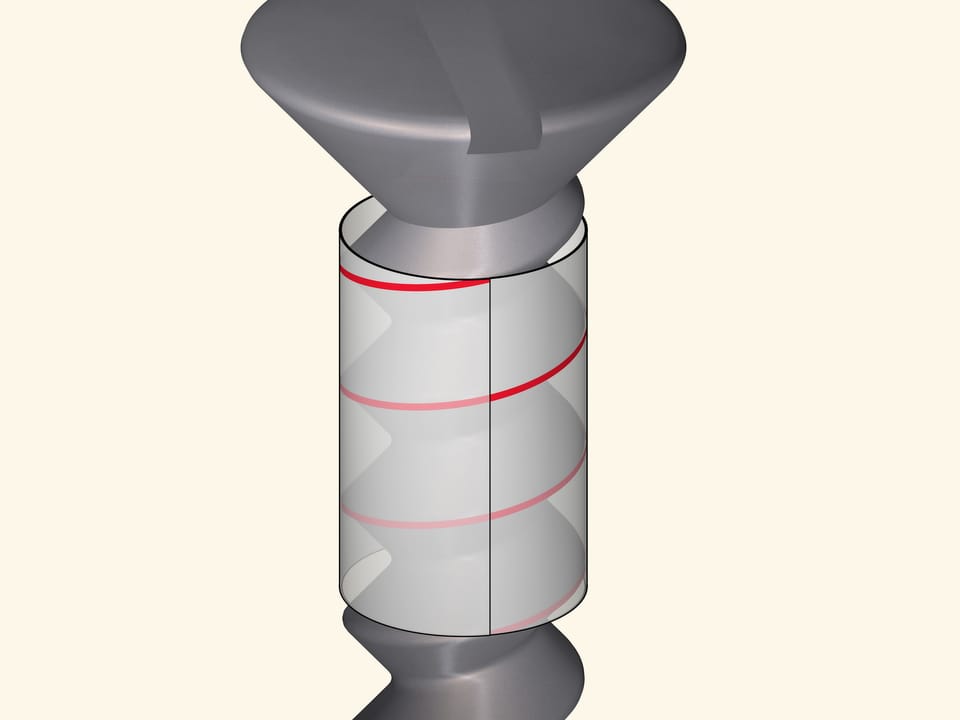
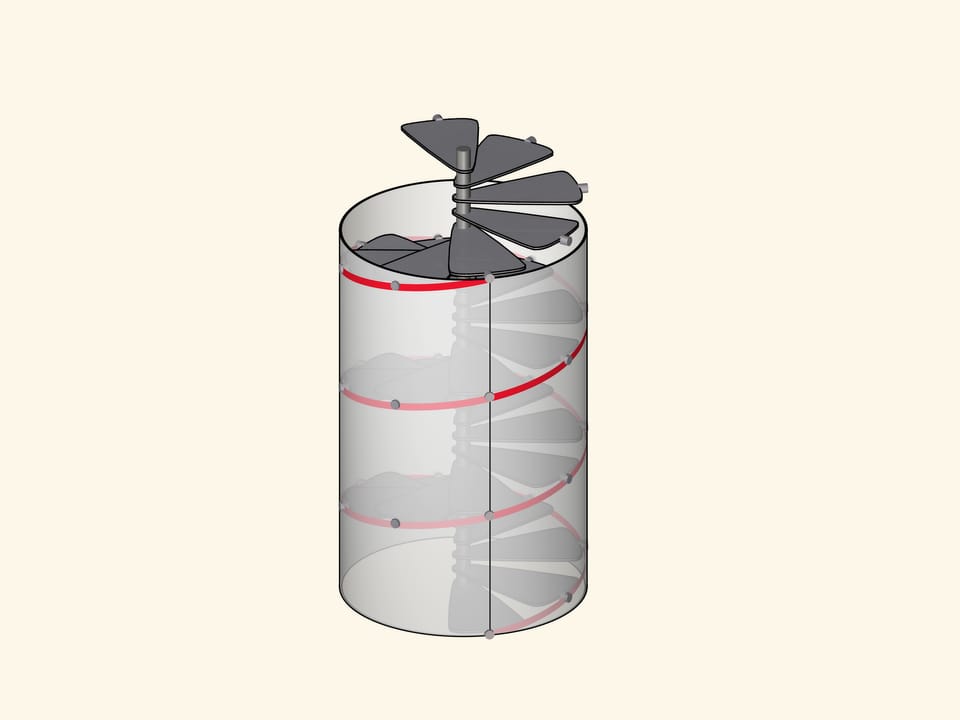
The ease with which a nut is screwed onto a bolt suggests that the thread is uniform along the entire length of the bolt, and the mathematical essence of threaded joints is the usage of a curve that can slide on its own. This remarkable curve is called a helix.
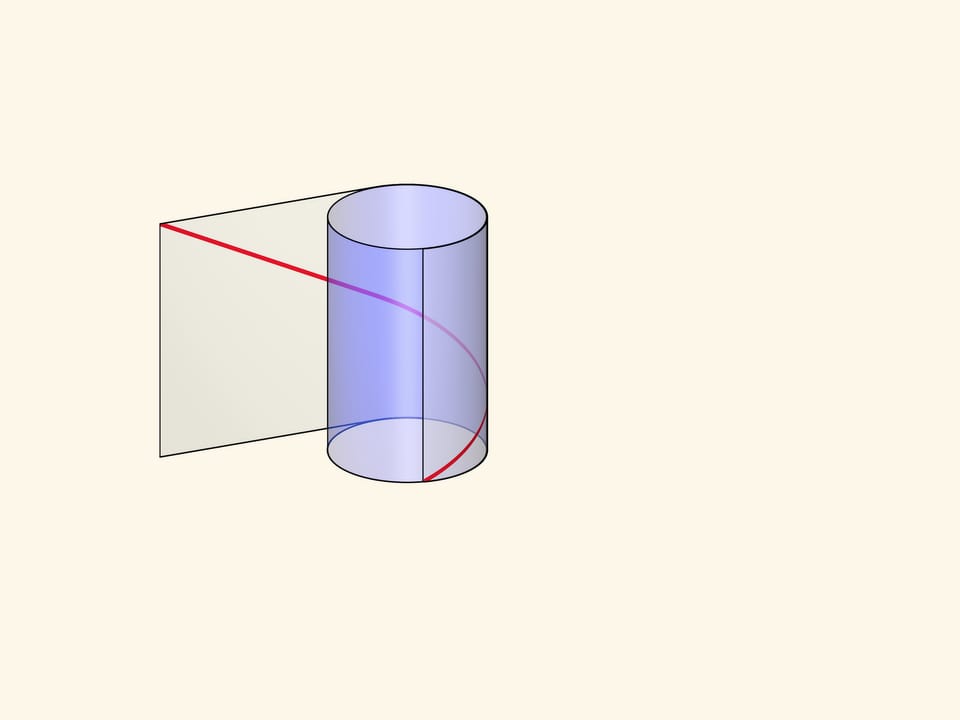
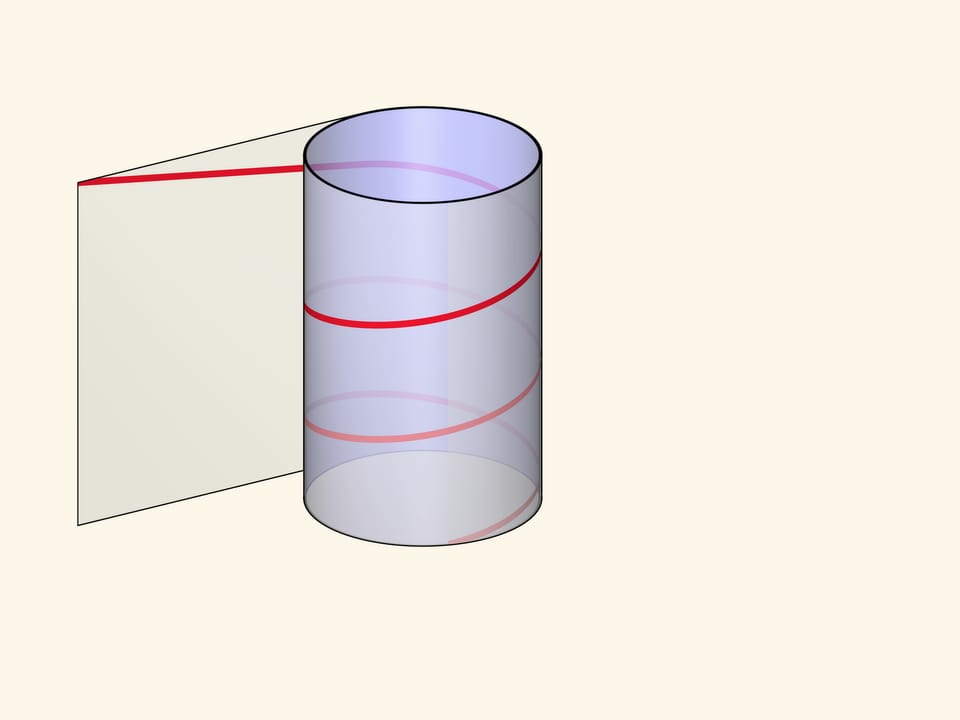
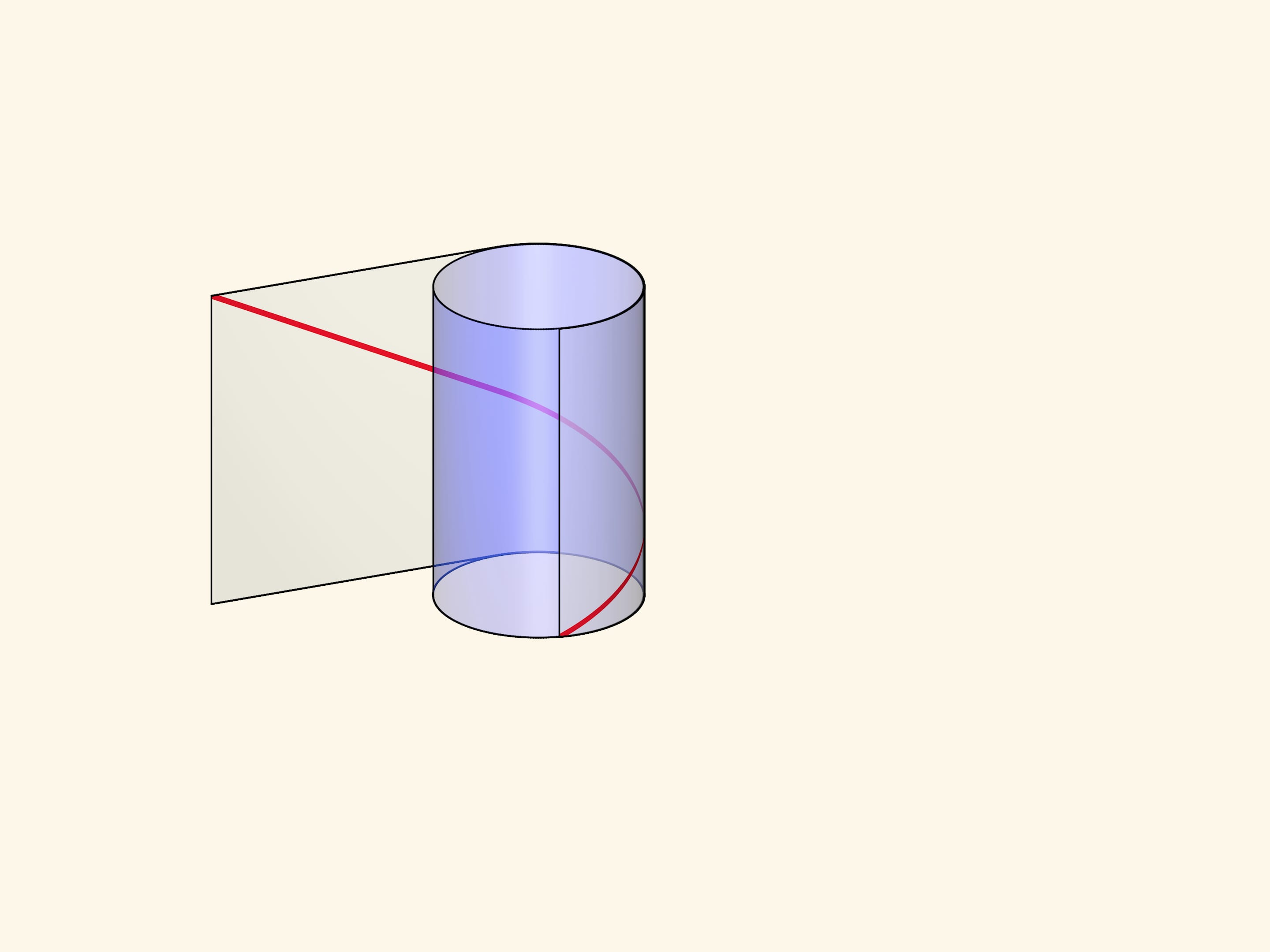
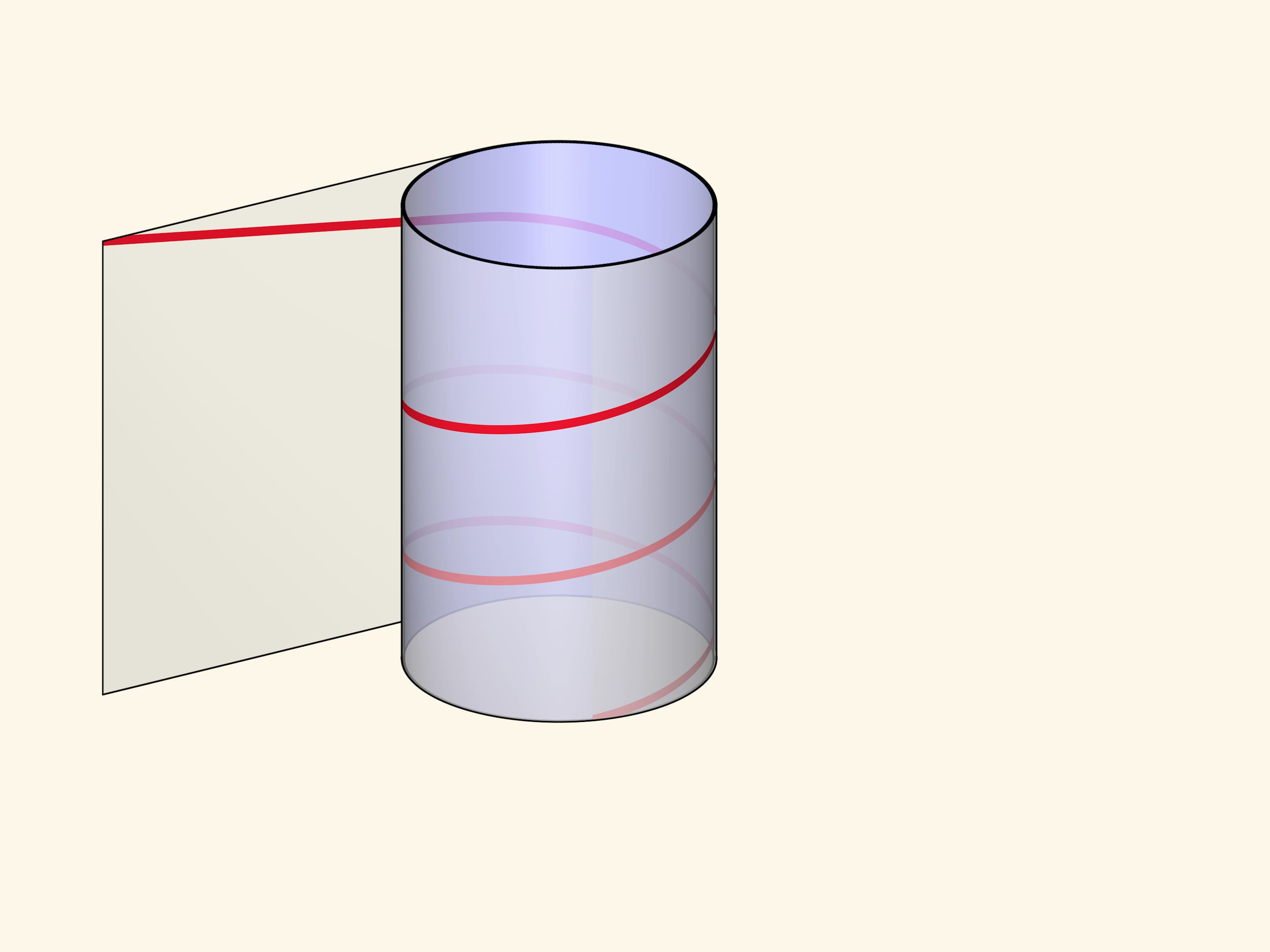
The helix can be made by winding a rectangular transparent sheet with a marked diagonal on a cylinder. Depending on the length of the sheet and, consequently, the angle of the drawn line, the pitch of the helix and the number of turns will vary.
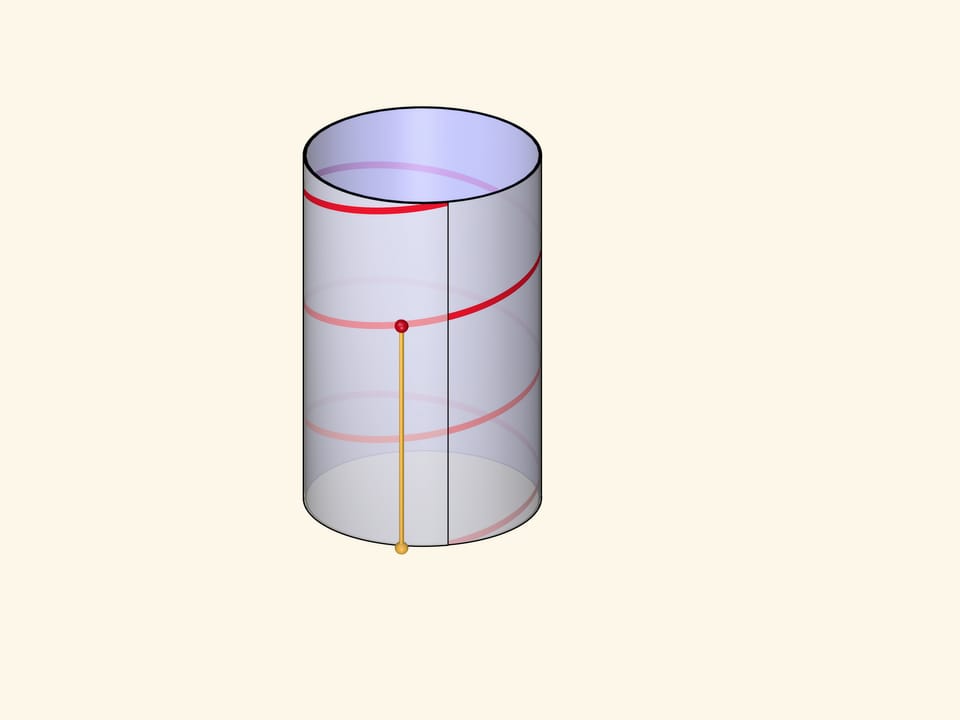
Formally, the helix (cylindrical) is a line defined by a point which rotates with constant angular velocity around a fixed axis and simultaneously moves along this axis with a constant velocity.
The visual representation and definition are combined in the parametric definition of the helix in a rectangular Cartesian coordinate system: $$ x=a \cos t,\quad y=a \sin t,\quad z=ht. $$ The first two equations show that the projection of a point runs along the base of a straight circular cylinder of radius $a$. The third equation defines the motion along the axis of the cylinder at a constant velocity.
“Good” curves have two basic properties in three-dimensional space — curvature and torsion.
Curvature is the speed at which the line curves on a plane and is defined by the radius of the circle whose arc best approximates the small segment of the curve containing the point in question. Torsion — the speed at which the curve tends not to be flat, how hard the curve “wants” to leave the plane.
Remarkably, for fairly smooth curves, curvature and torsion completely define its shape.
For the helix, curvature and torsion are constant, and the above statement implies that only helices do have such a property!
The constancy of curvature and torsion at all points means that the structure of the helix is uniform over all points. As a consequence, it follows that a segment of a helix can slide along it in the same way as a segment can slide along a straight line and an arc of a circle can slide along its circumference. (A straight line and a circle can be considered as degenerate, extreme cases of the helix).
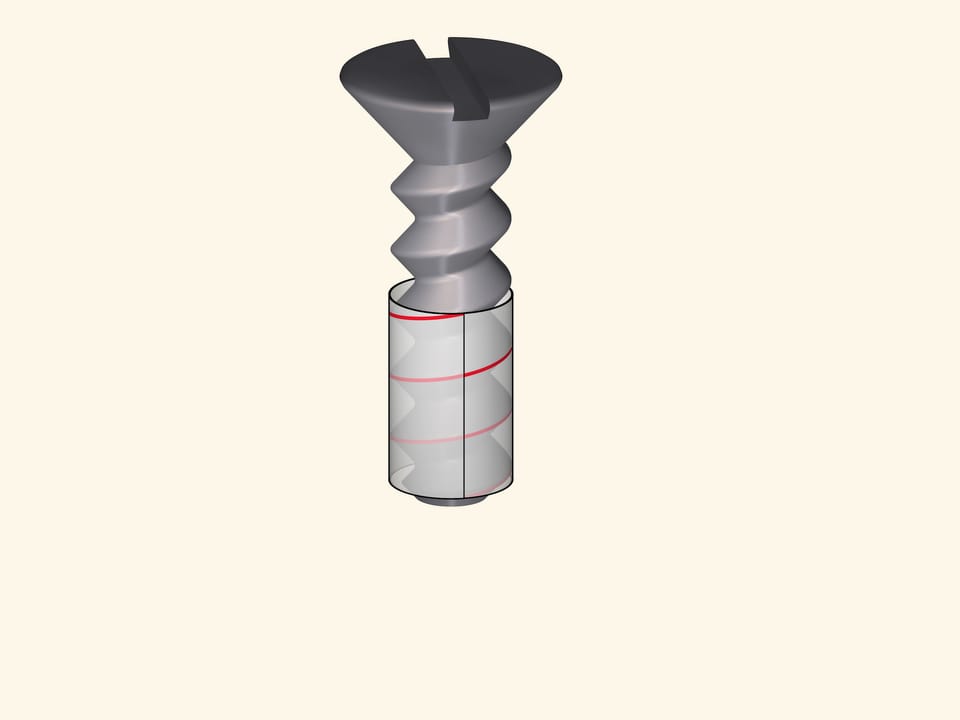
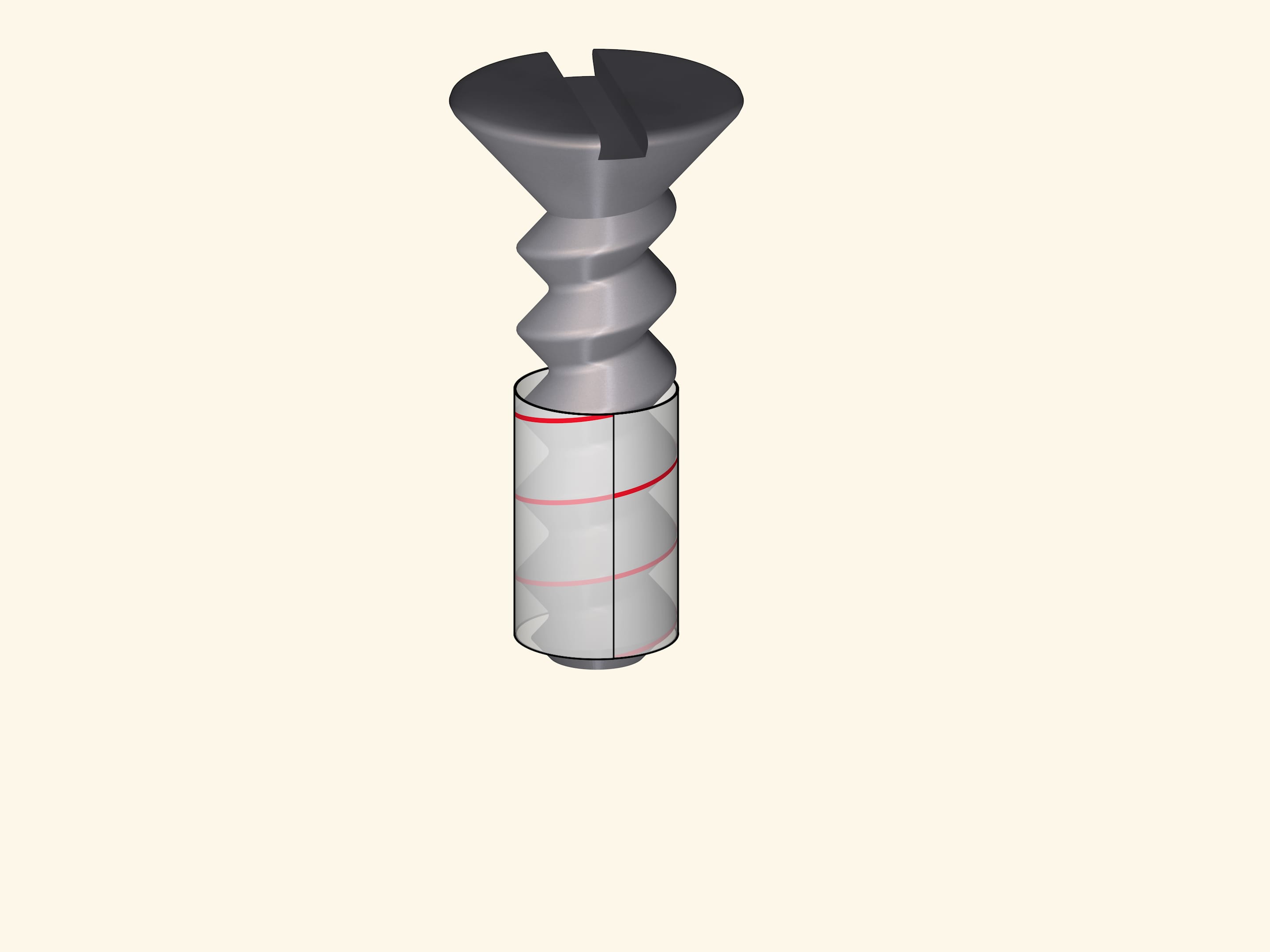
Threaded joints, a particularly bolt or screw, are based on a helix. When screwed in, the thread slides as if on a track.
The helix is the only curve that can slide on its own. And in engineering problems, where the presence of such a property is desirable or even necessary, it is impossible to do without helices.
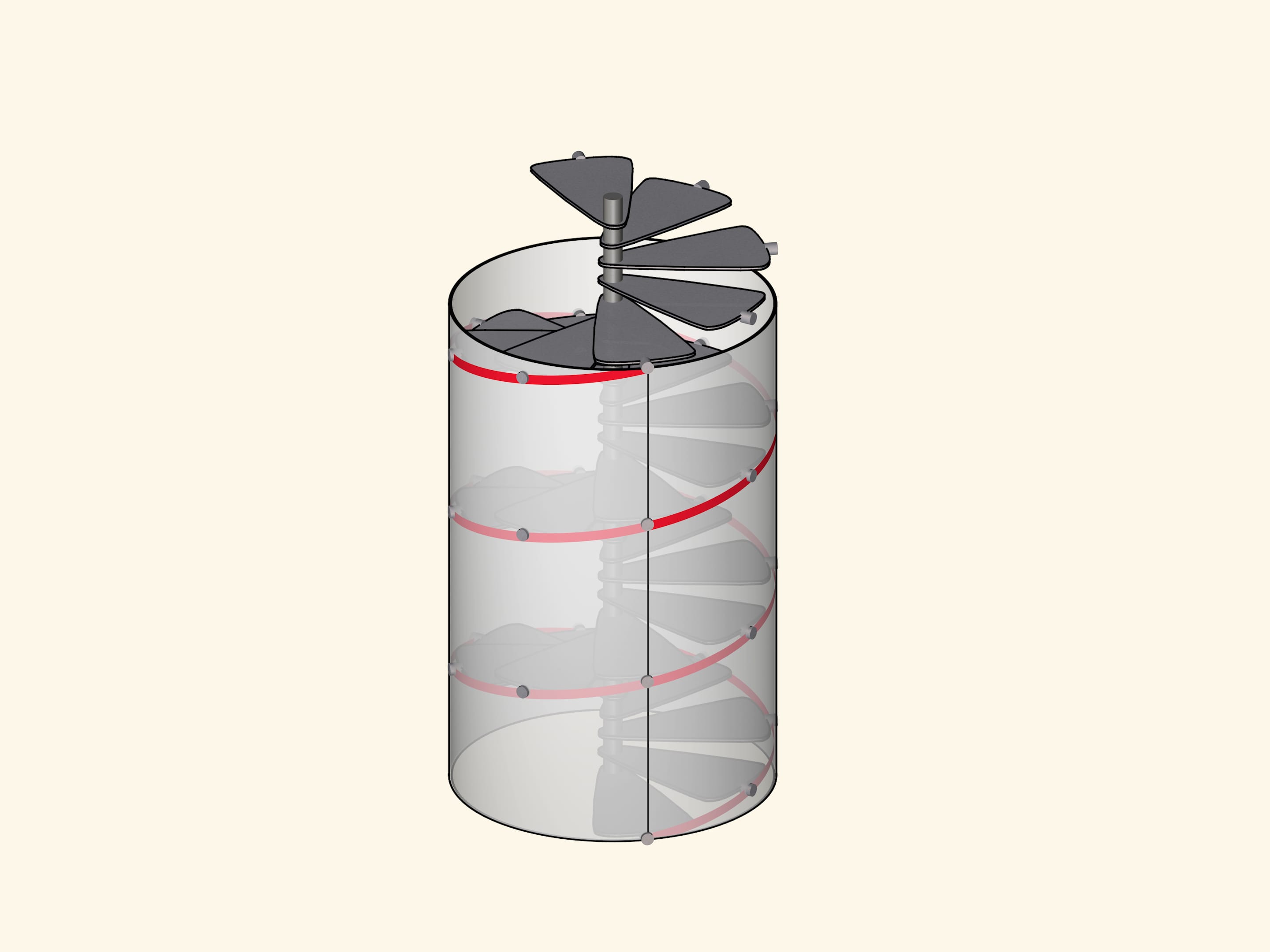
The helix is also the boundary of spiral staircases. Climbing up, you are by definition moving upwards at a constant speed. Both a corkscrew and a fishing auger have the shape of a spiral line, sliding in the material along the path already taken.