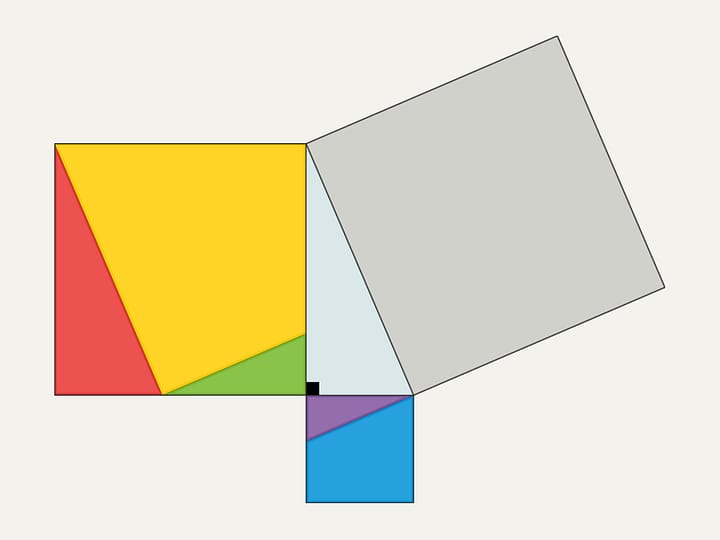
Calculation of the area of a polygon
with vertices at the nodes of checkered paper.
with vertices at the nodes of checkered paper.
Enter the area of the «simple» triangle.
A «simple» triangle — no grid nodes neither inside
nor on sides, except for vertices.
nor on sides, except for vertices.
Statement. Any polygon with vertices
in grid nodes can be triangulated,
i.e. split into «simple»triangles.
in grid nodes can be triangulated,
i.e. split into «simple»triangles.
Draw a non-self-intersecting polygon.
$ S = N_1 /2 + N_2 - 1$
Unit of measure — squared parrot.
Please don't disturb.
Please don't disturb.
Area of a polygon with integer coordinates is $${\color{#359BE1}S} = {\color{#40b521}N_1} /2 + {\color{#E64D15}N_2} — 1,$$ where ${\color{#40b521}N_1}$ — the number of integer points on the polygon's boundary, and ${\color{#E64D15}N_2}$ — number of integer points that are interior to the polygon.