Can one fold a development of a polyhedron into a closed body, whose borders will be not parts of planes but rather pieces of smooth surfaces?
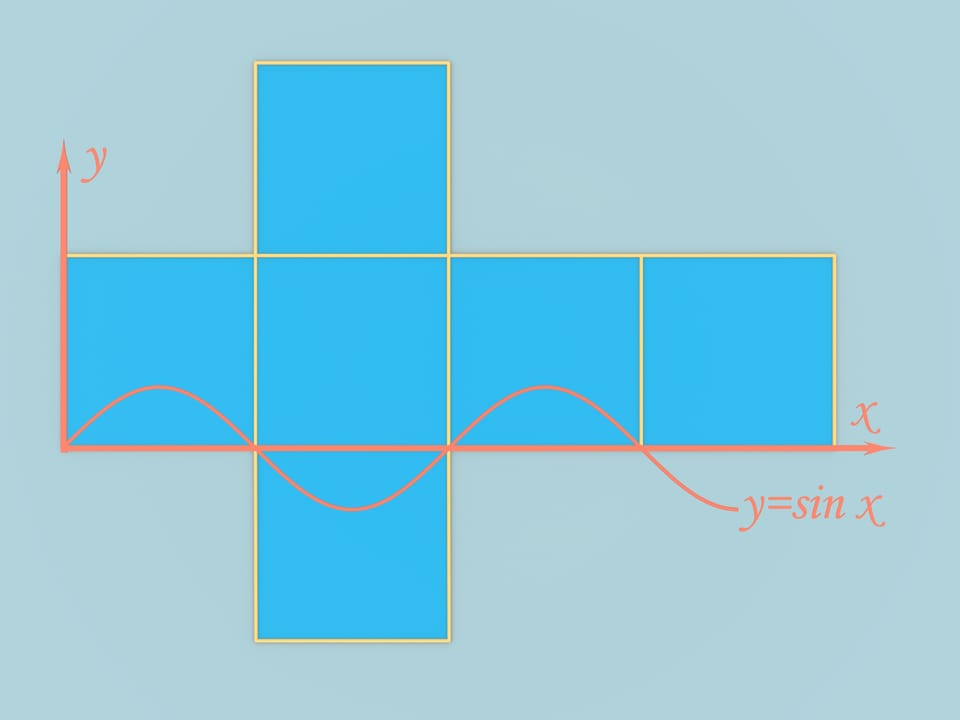
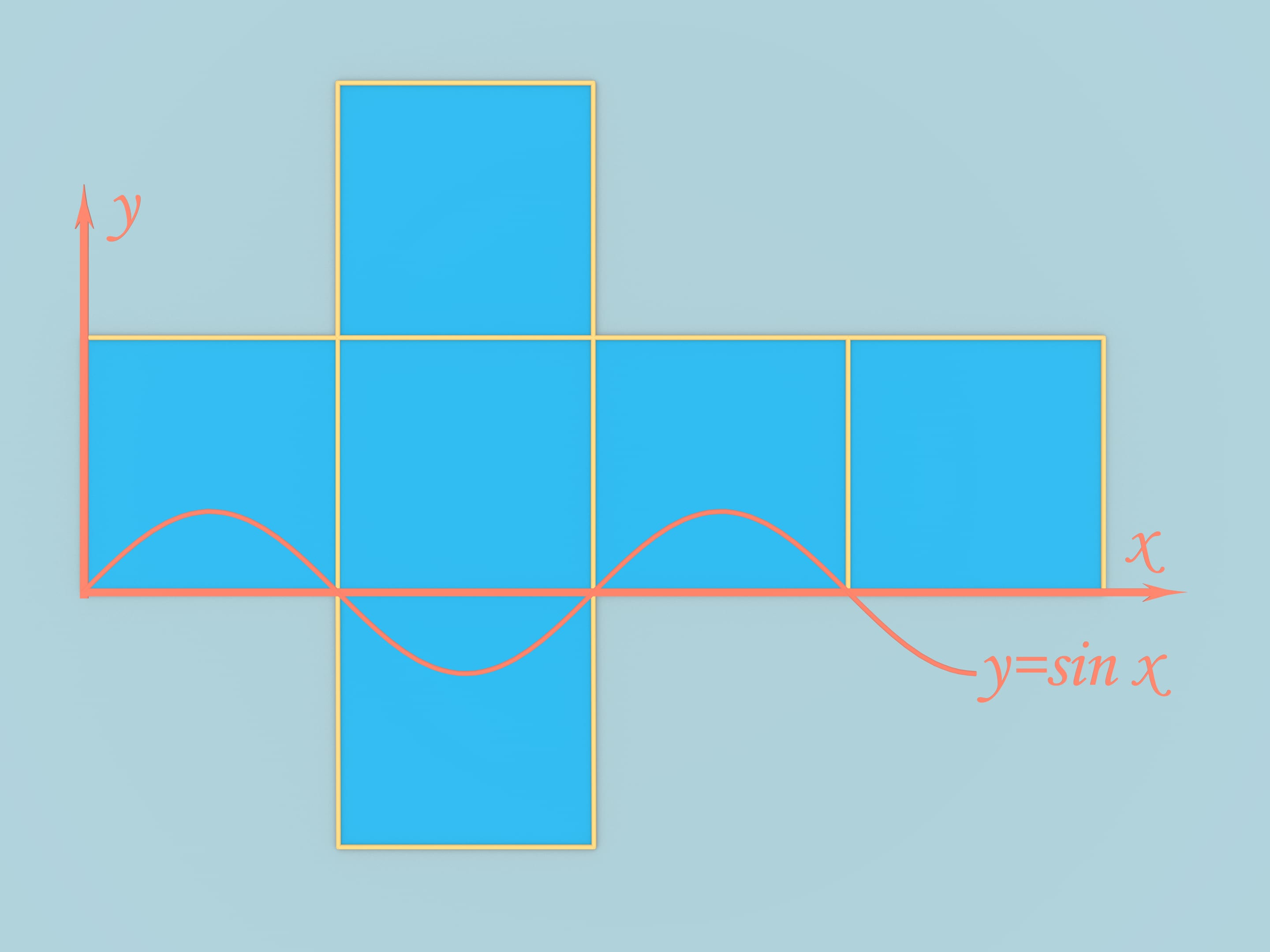
Take a cube with edge length equal to $\pi$. Unfold it into the cruciform development and plot a graph of the function this body.
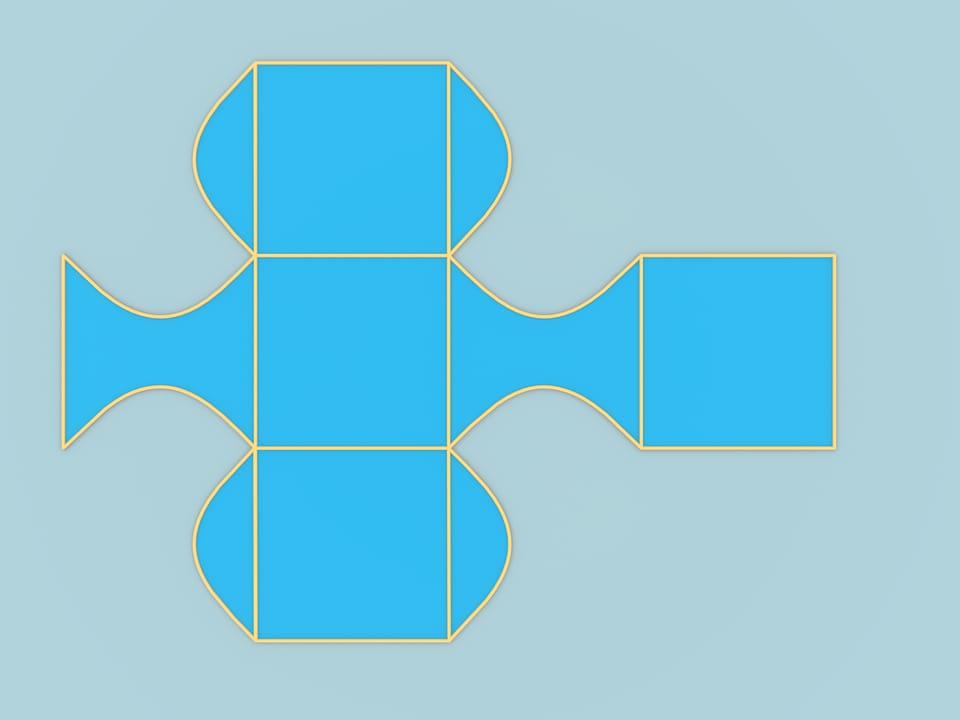
While the example we considered answers the question, it has a big disadvantage. It's border contains two pieces that remained form the cube and are plane. Having built this example, a construction that doesn't have this disadvantage appeared really quickly.
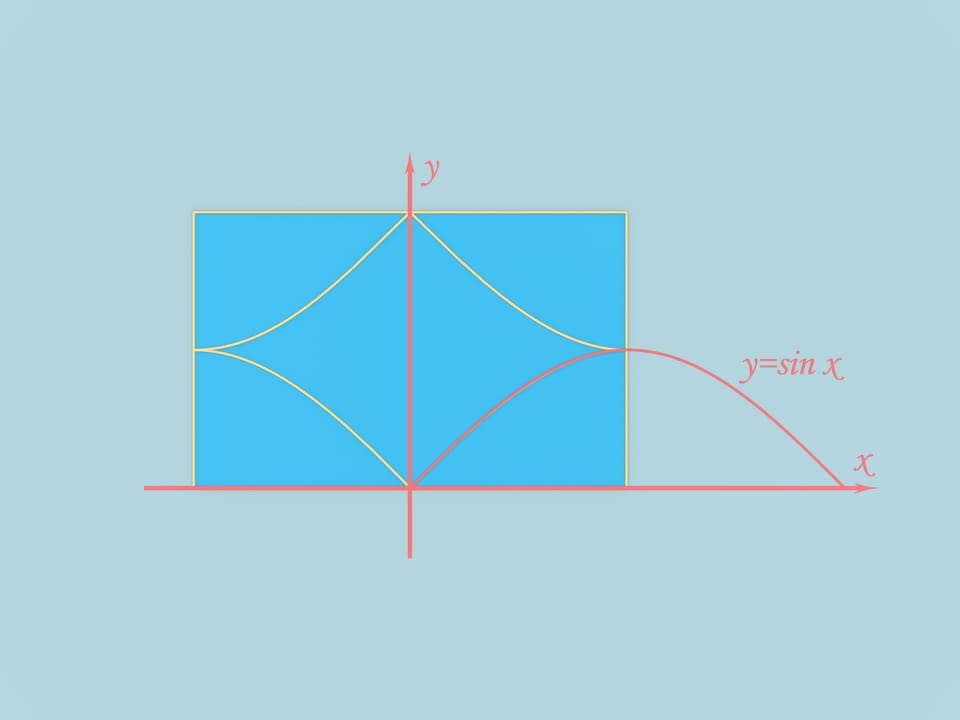
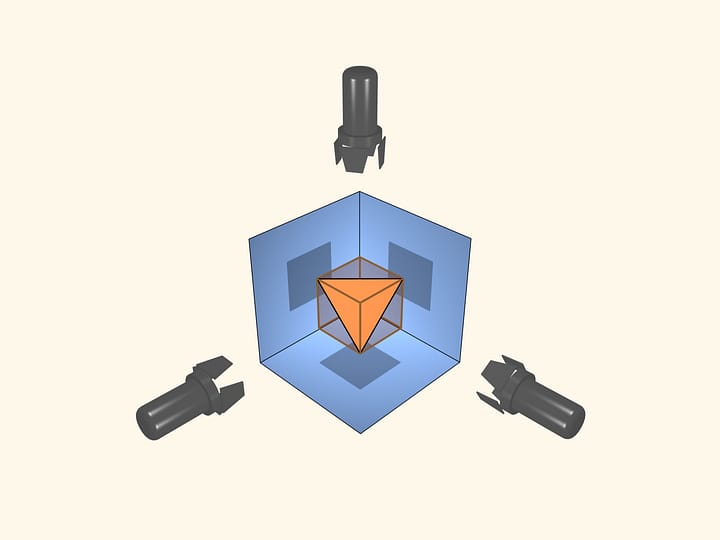
Take a rectangular sheet of paper with the edge ratio $\pi/2$. As any rectangular sheet, we can fold it into a triangular pyramid. To do that just draw edges connecting the centers of neighbor sides and an edge connecting the middles of the longer sides. Folding along the edges one gets a triangular pyramid.
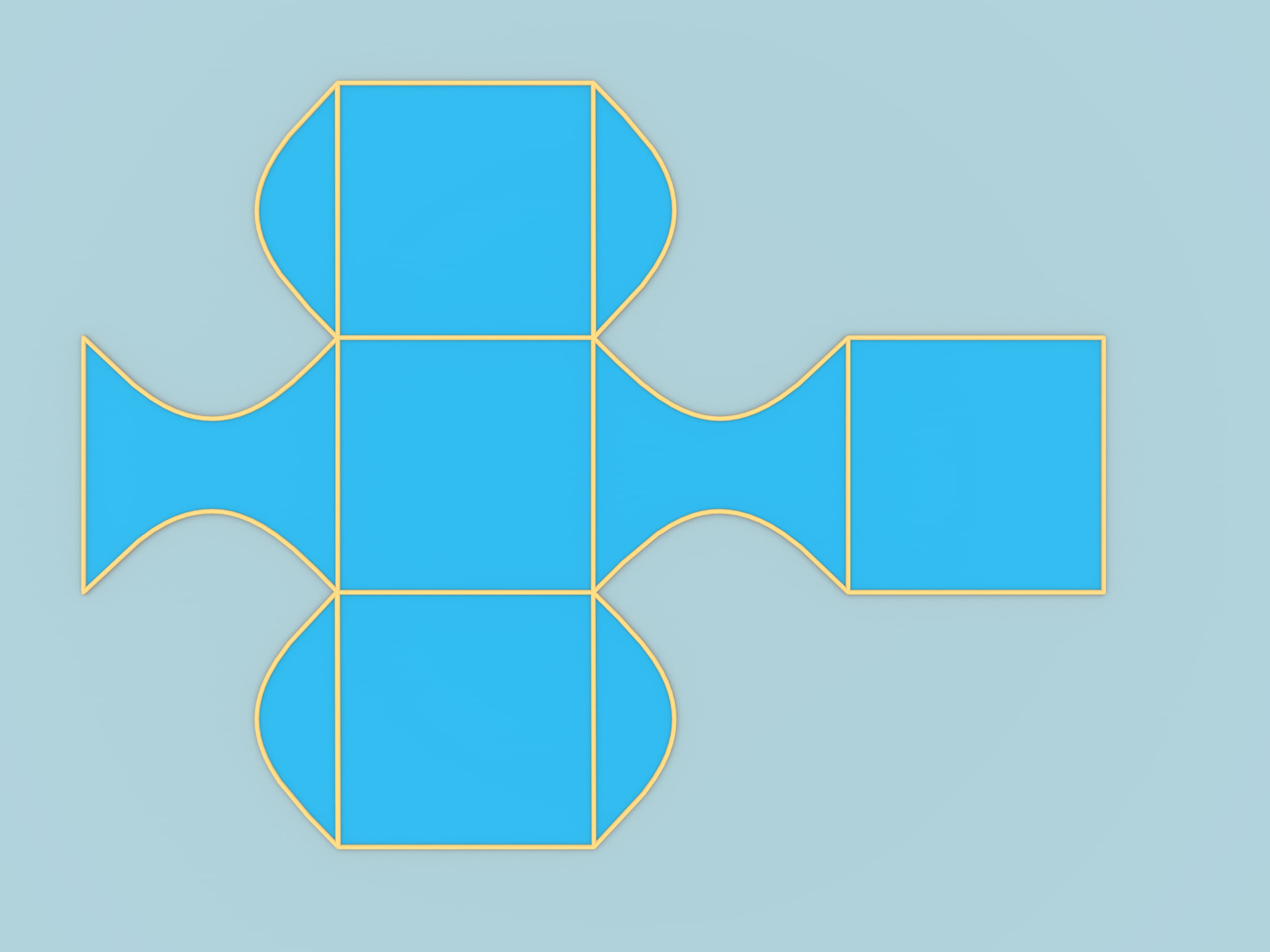
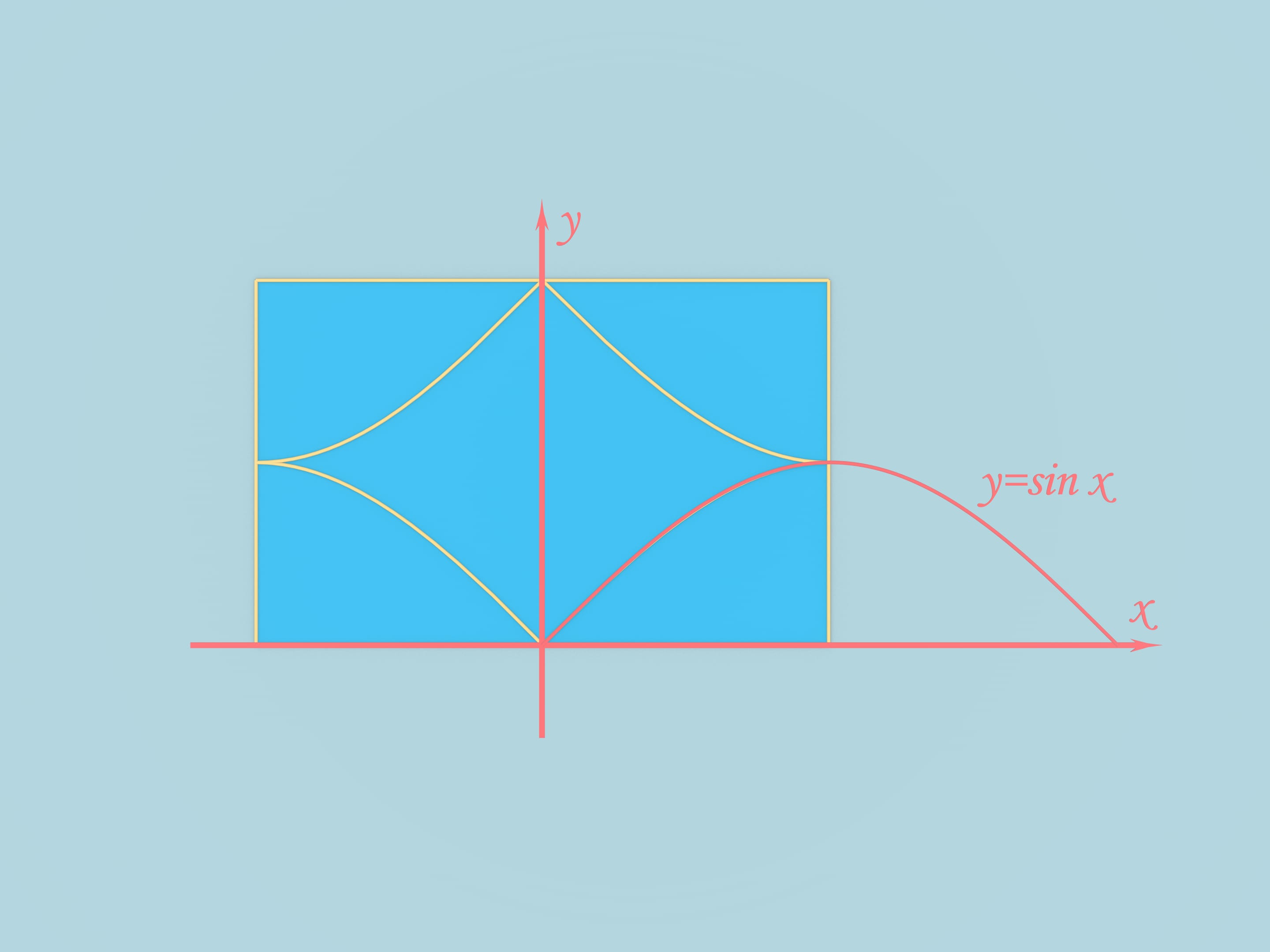
From the same sheet of paper we can get another figure, whose surface will be constructed of smooth parts. Connect the middles of neighbor sides with three cylinders — two tangent and one perpendicular to them. Thus, the border is constructed of pieces of cylinders.
It's amazing how young mathematics is. It seems that such examples should have existed maybe not along with Archimedes, but long long ago. But in fact, the examples we considered appeared only during the fall 2004.
Other etudes in “Polyhedra’s outer geometry”
