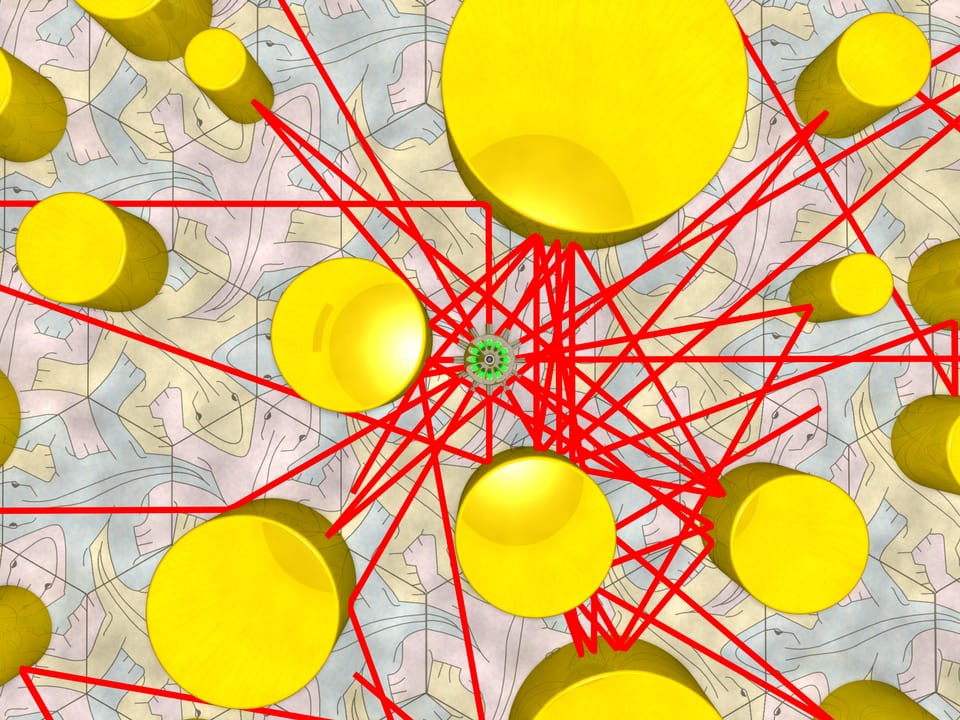
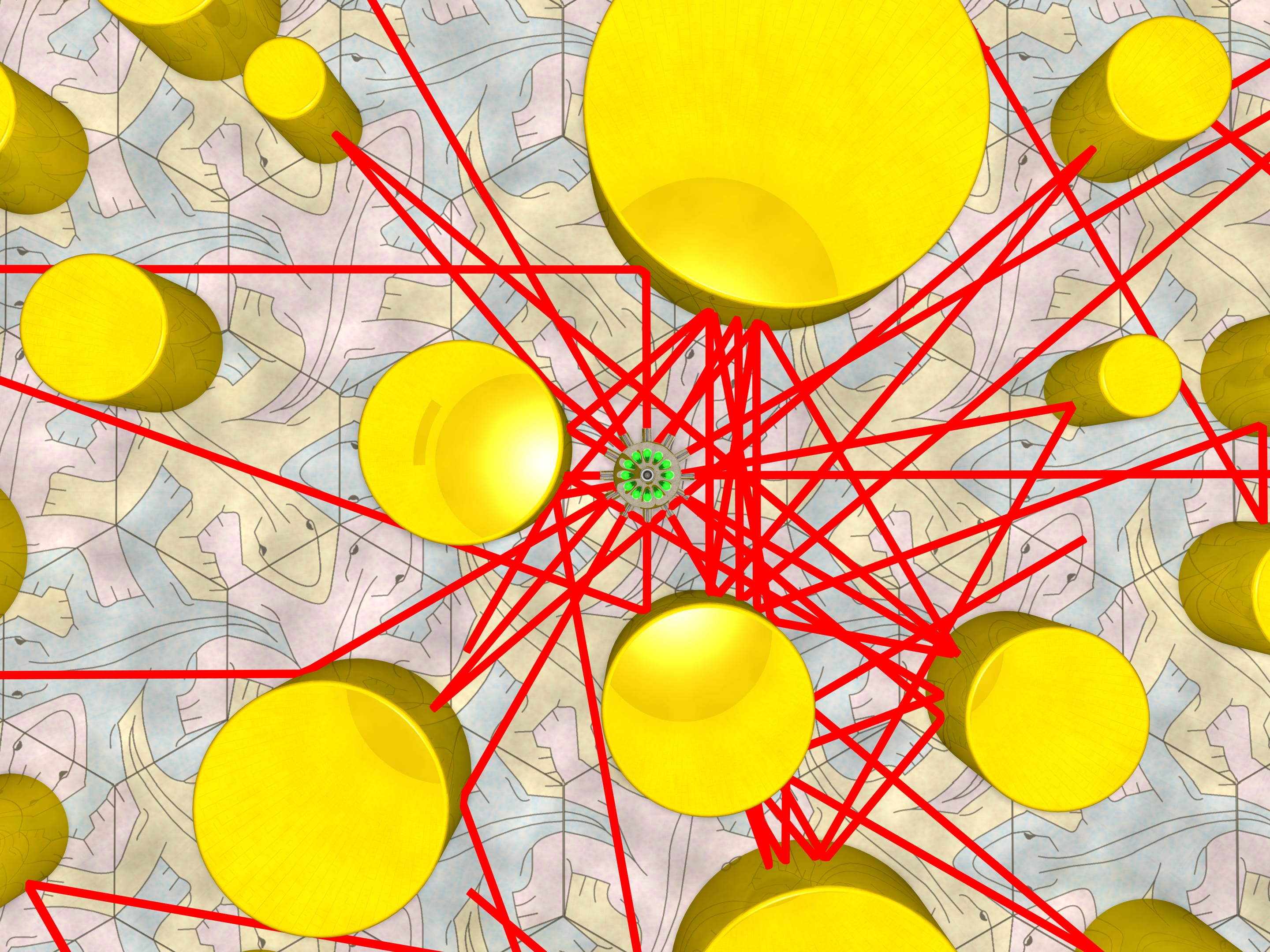
Is it possible to place round mirror columns so that a ray with arbitrary direction parallel to the floor never reaches the walls? Columns with reflecting cylindric side surface may be of any diameter and can be placed anywhere with a single condition: they shouldn't be tangent (if not the answer is obvious).
As we know, the law of reflection is «the angle of incidence is equal to the angle of reflection». If the mirror is not plane we should just measure the angles off the tangent plane to the point of reflection.
How many columns do you need and how they should be placed so that a ray is shielded and doesn't reach the walls? Do we need finitely many mirrors or a infinite number of them? Or even that is not enough?
It's clear that one column is not enough. A ray can pass by the column, but even if it reflects it will reach the wall. Thus, a ray with any direction will finally reach the wall.
It's obvious that two or three columns is not enough; the walls will remain visible in some directions from the center of the hall. And so, if we radiate in this directions we'll reach them.
Intuition tells us and an experiment shows that a small amount of columns is not sufficient to shield a ray.
Place rays reach the walls.
Well, an experiment is not a proof. Maybe we should rearrange the columns or take some more… It's still an open question for mathematicians if a finite number of columns (maybe a very large) is sufficient to shield a ray. If it is, what are their diameters and positions? Or maybe even an infinite number of columns is not enough to solve the problem?
Maybe You will find out how to place the columns?