Here is Luch-2, the eight-millimeter film projector. It was in every Russian house where cine amateurs shot and looked films.
This cartoon presents geometrical notion often studied at mathematical circles and its applications in our everyday life.
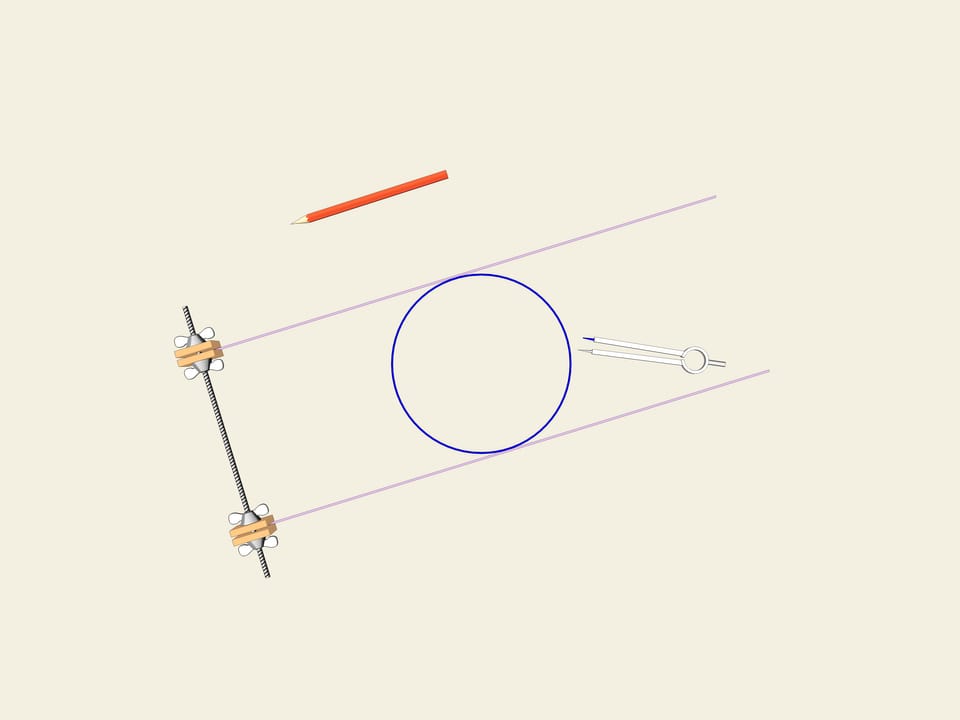
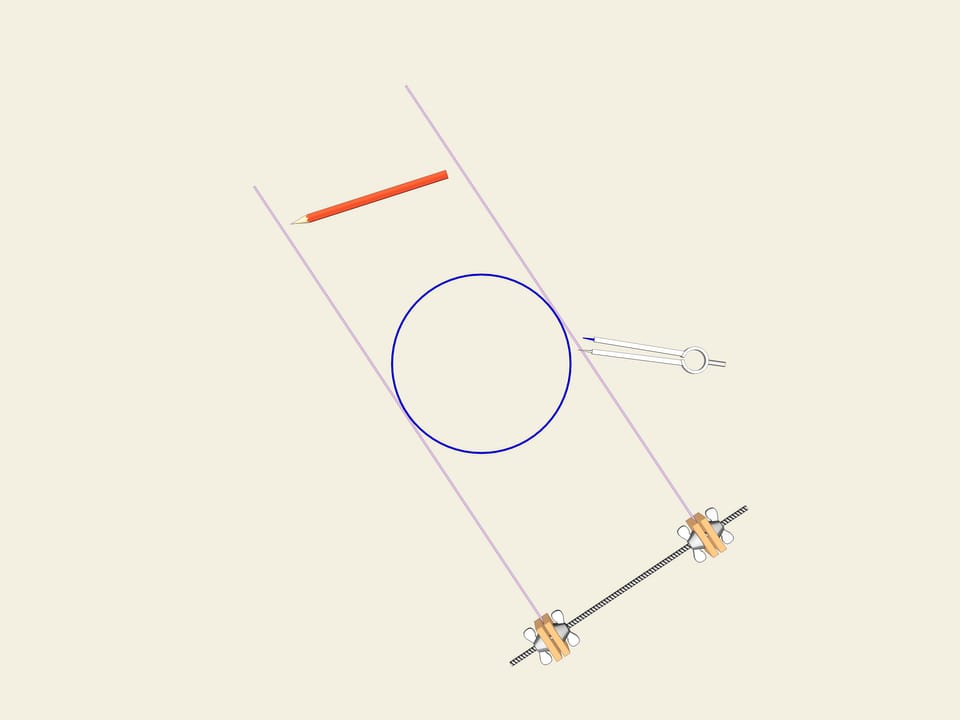
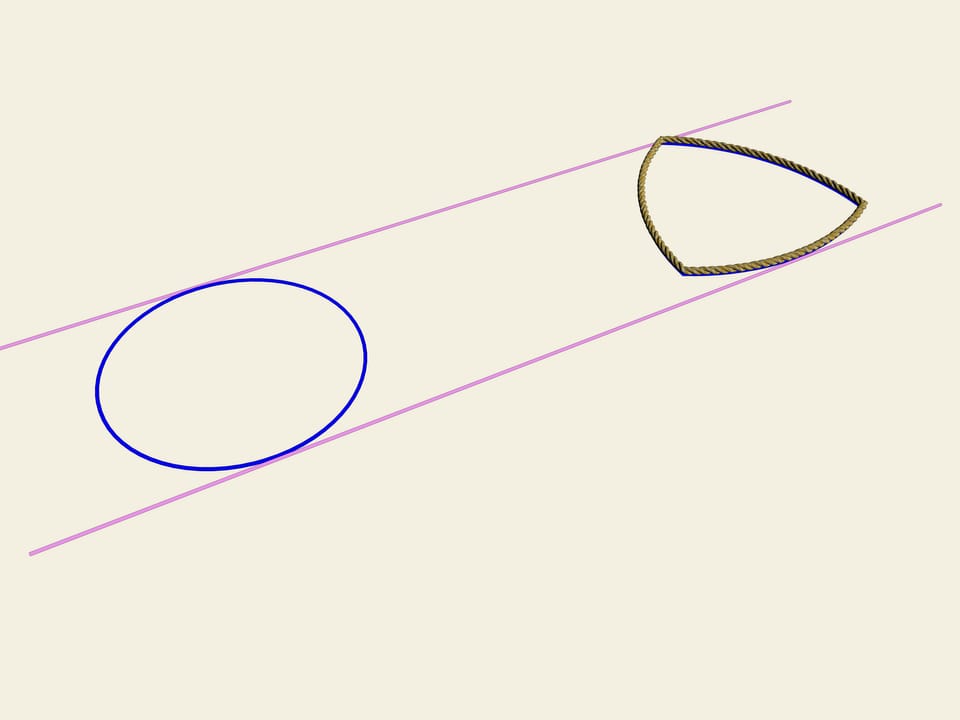
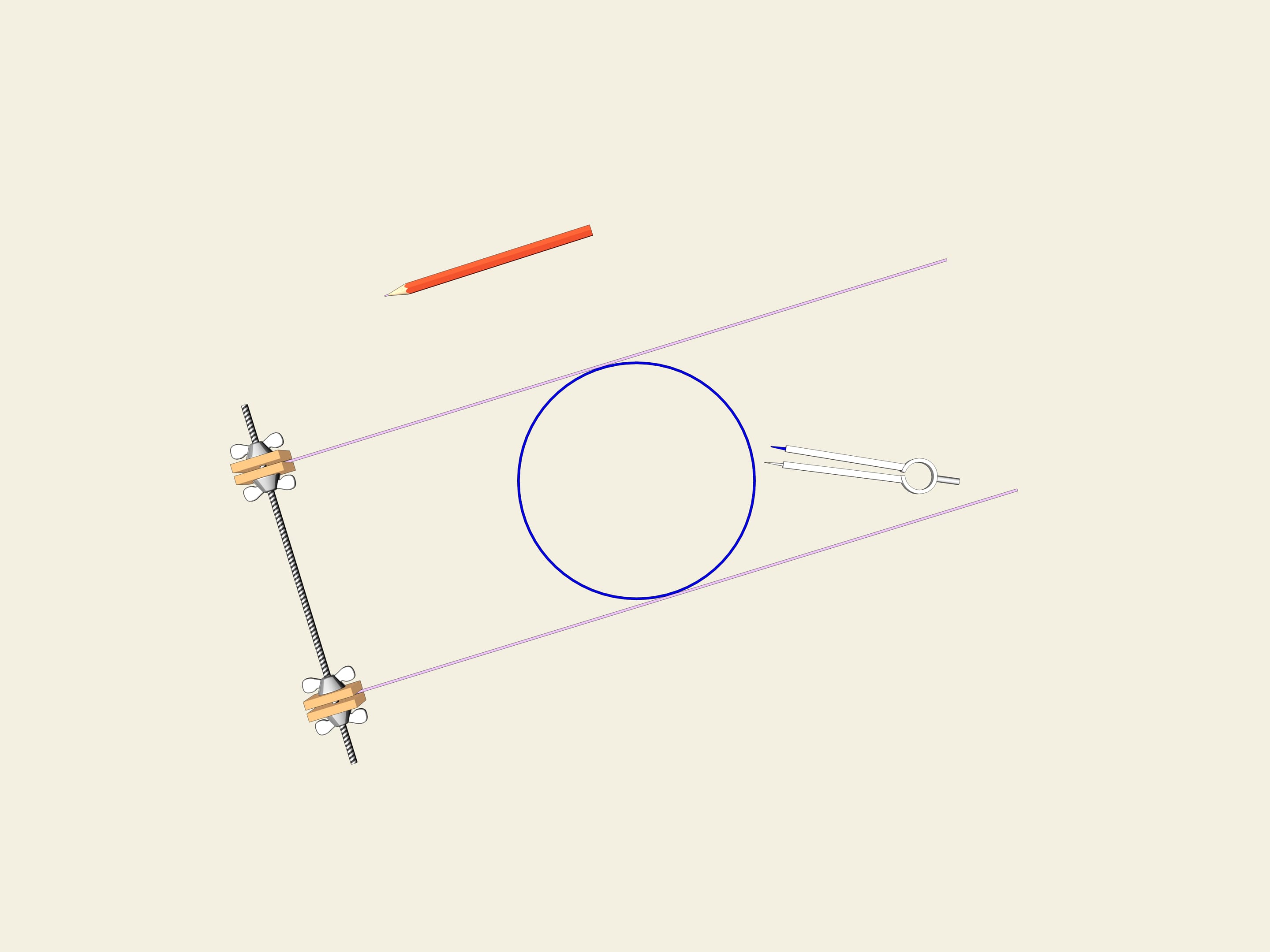
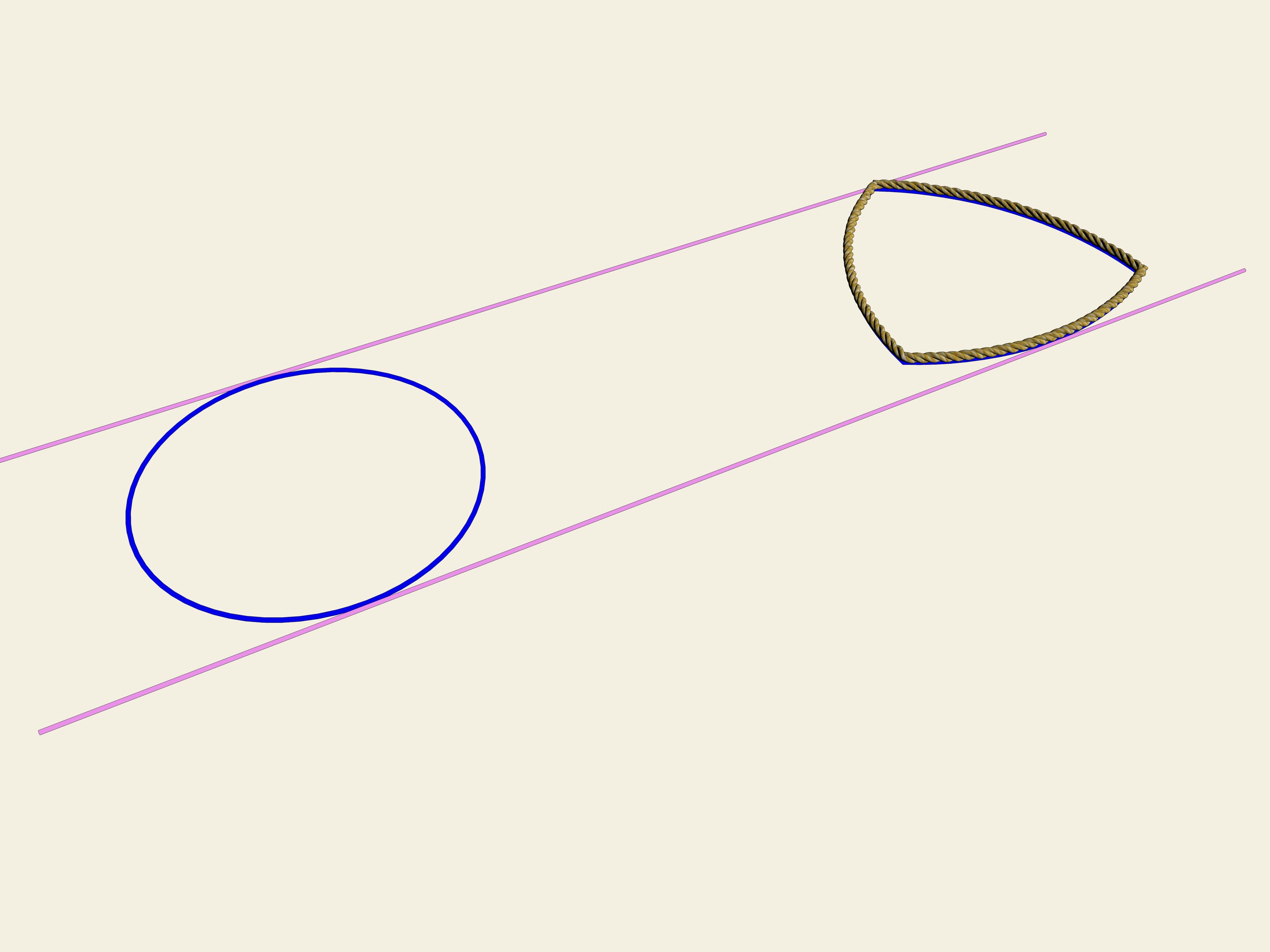
A wheel... A circle. One of the properties of a circle is its constant width. Let's draw two parallel lines and fix the distance between them. Let’s start to rotate them. The curve(the circle in this case) permanently touches both lines. This is the definition that closed curve have constant width.
Wether there are curves various from circles with constant width?
Reuleaux, Franz 1829—1905
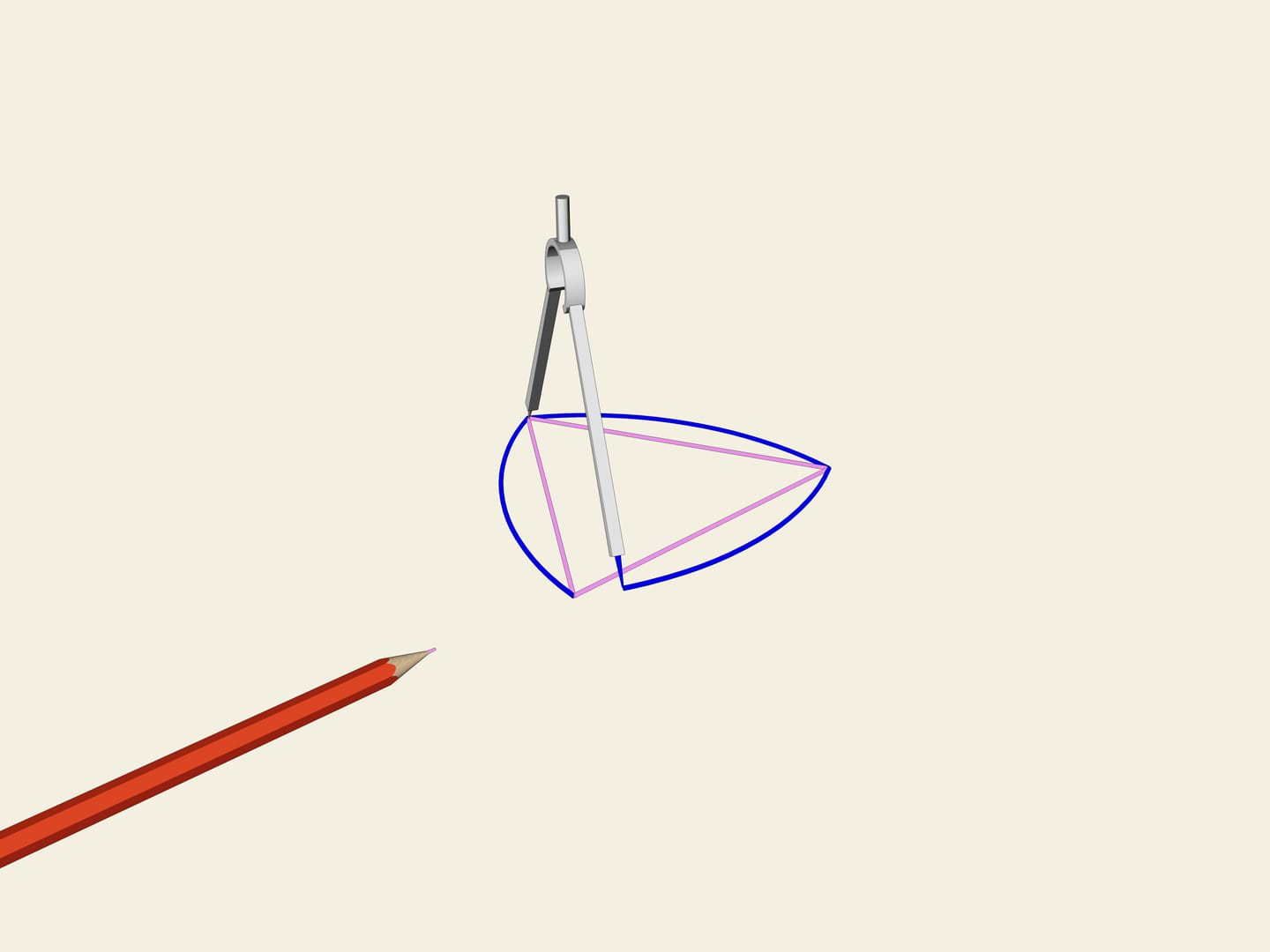
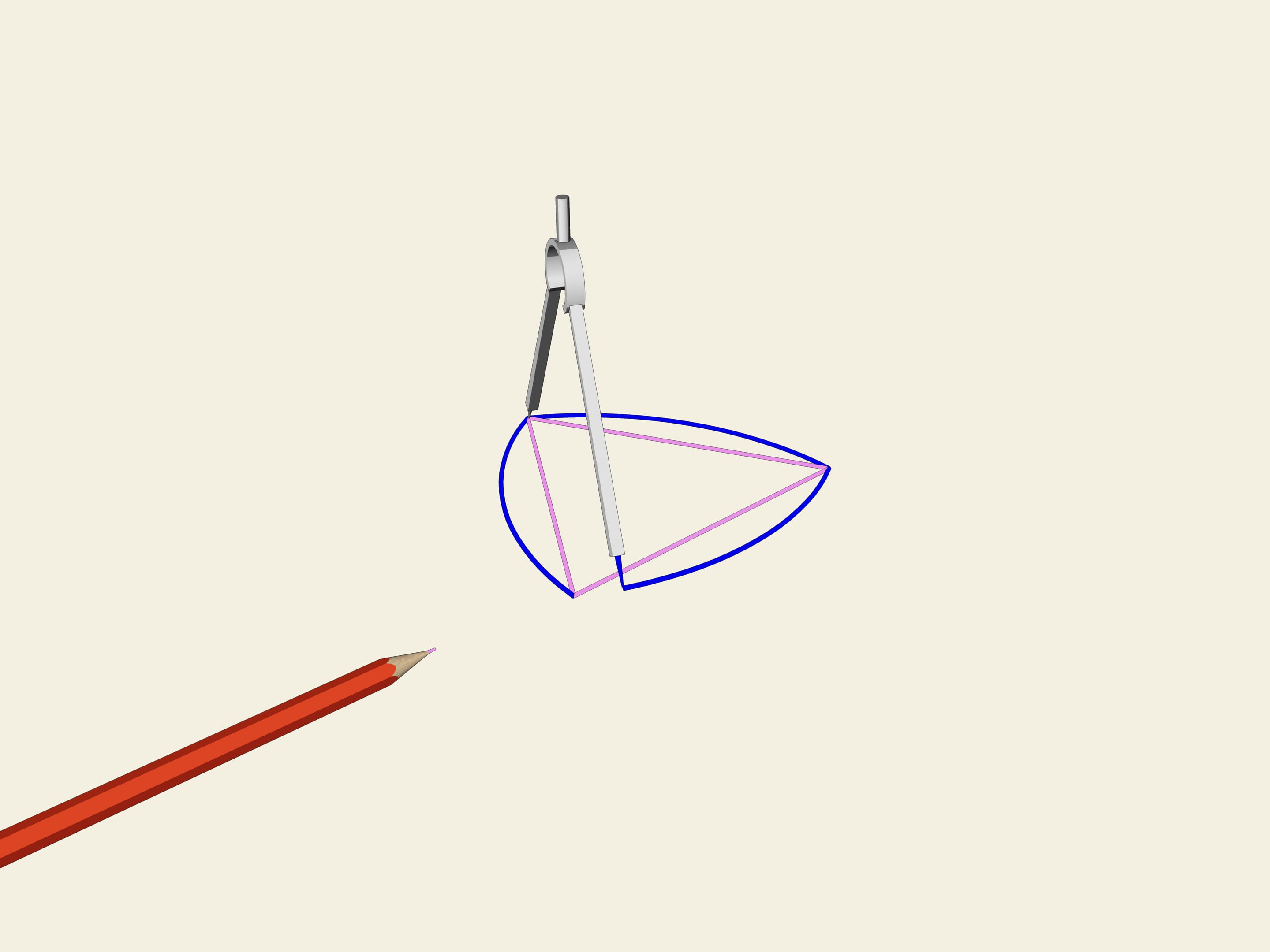
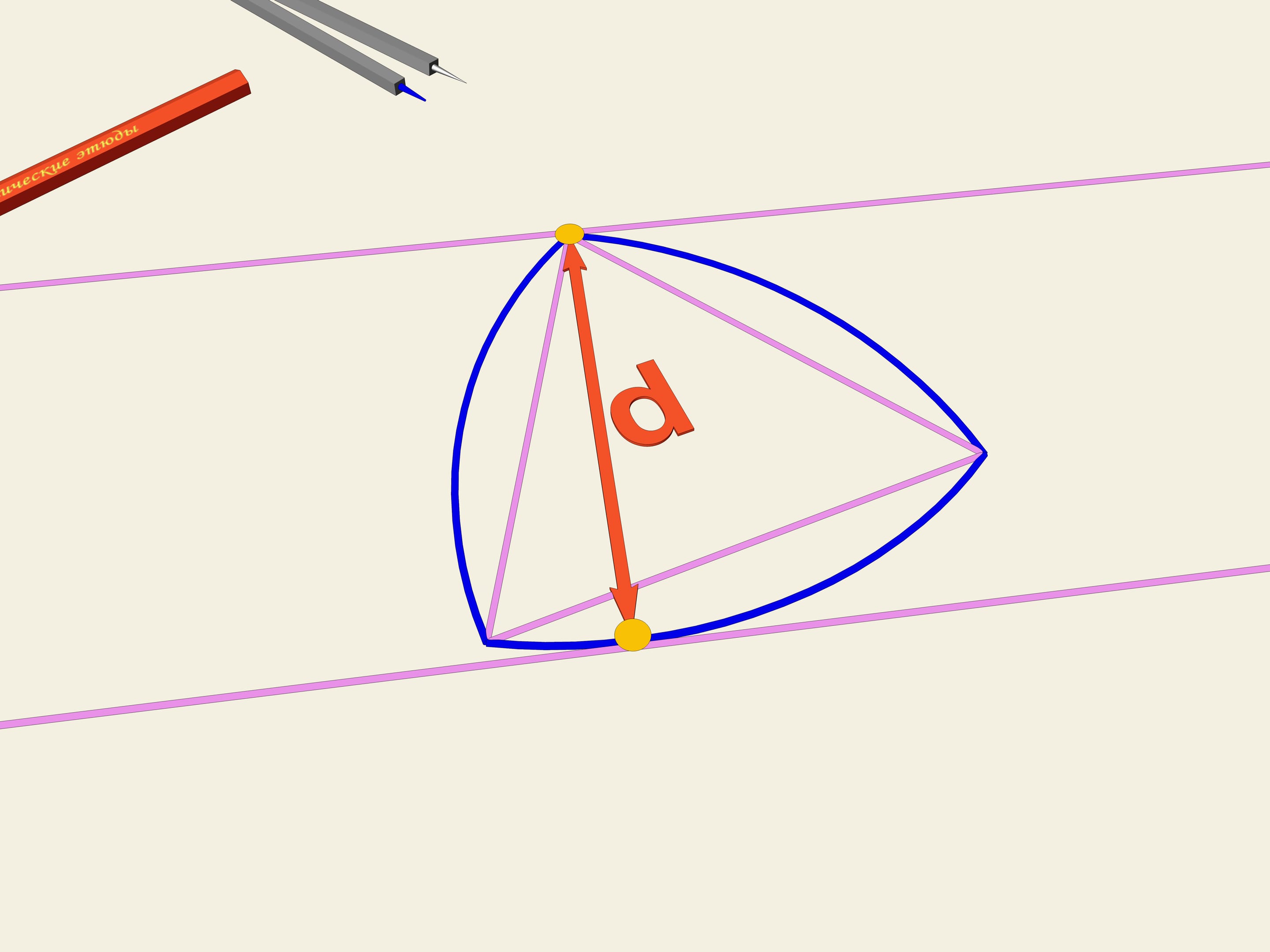
We consider a regular triangle. On each side of the triangle we shall draw an arc of a circle of radius equal to the length of the side. This curve is called "Reuleaux triangle". It turns out that this is a constant width curve. As well as in the case of a circle we shall draw two tangents, we shall fix the distance between them and we shall start to rotate them. Our curve continually touches both lines. Indeed, one of the points of contact is always situated at one of the "corners" of Reuleaux triangle, and the other on the opposite arc of the circle. Therefore the width is always equal to the radius of the circles, i.e. it is equal to the length of the initial triangle’s side.
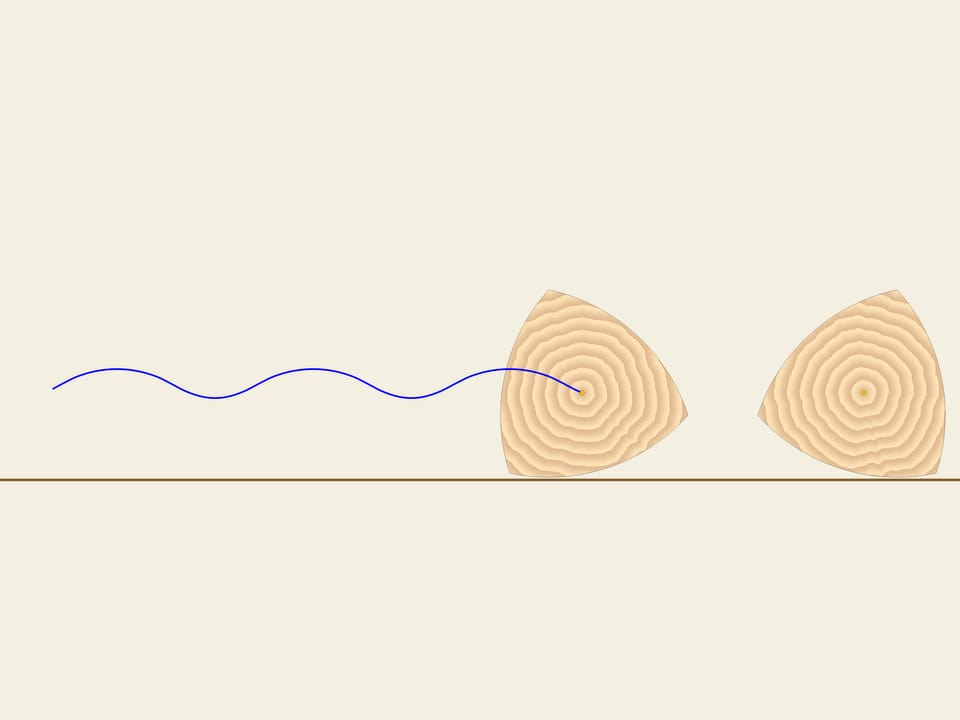
In an everyday sense constant width of a curve means that if one make wheels with such profile then a book will roll over them without stirring.
However it is impossible to make a wheel with such profile since the center of this figure describes a complicated line while rolling.
Whether there are another constant width curves? It turns out that there are infinitely many of them.
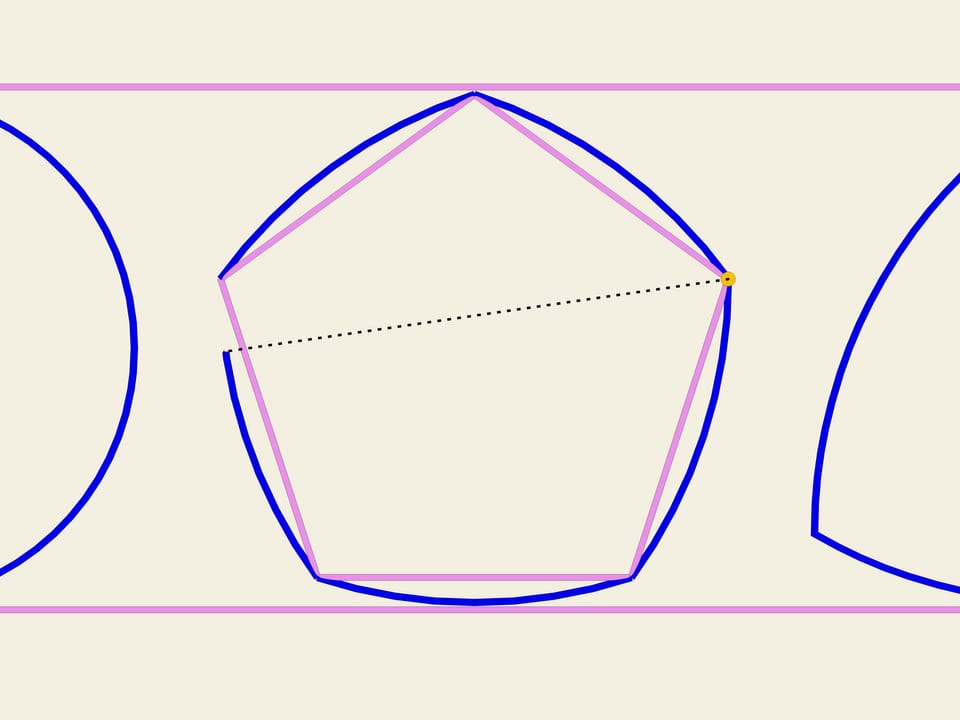
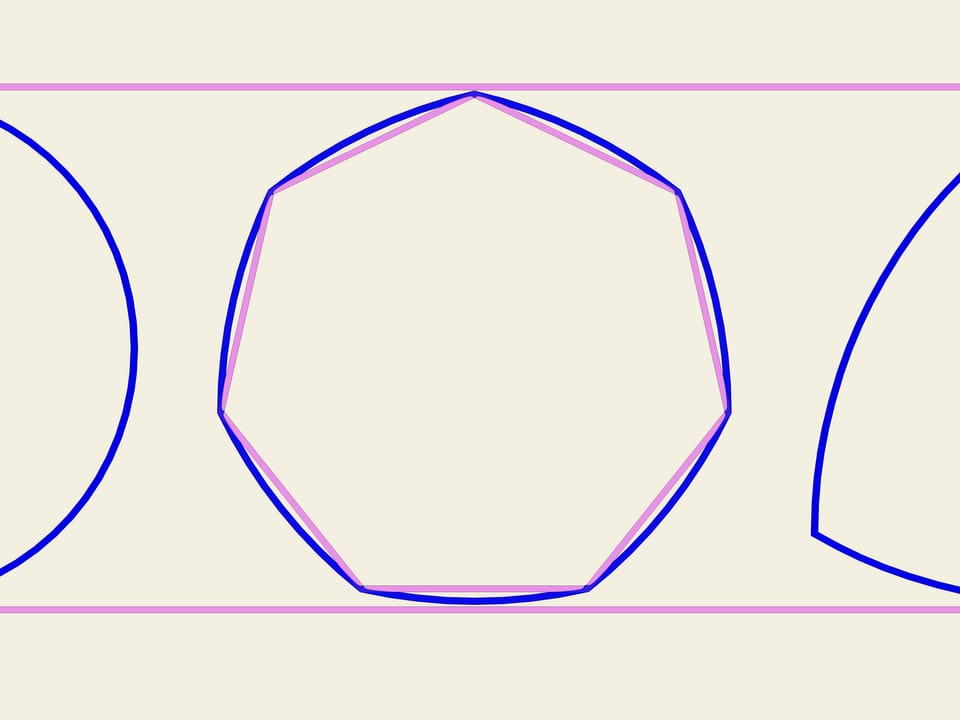
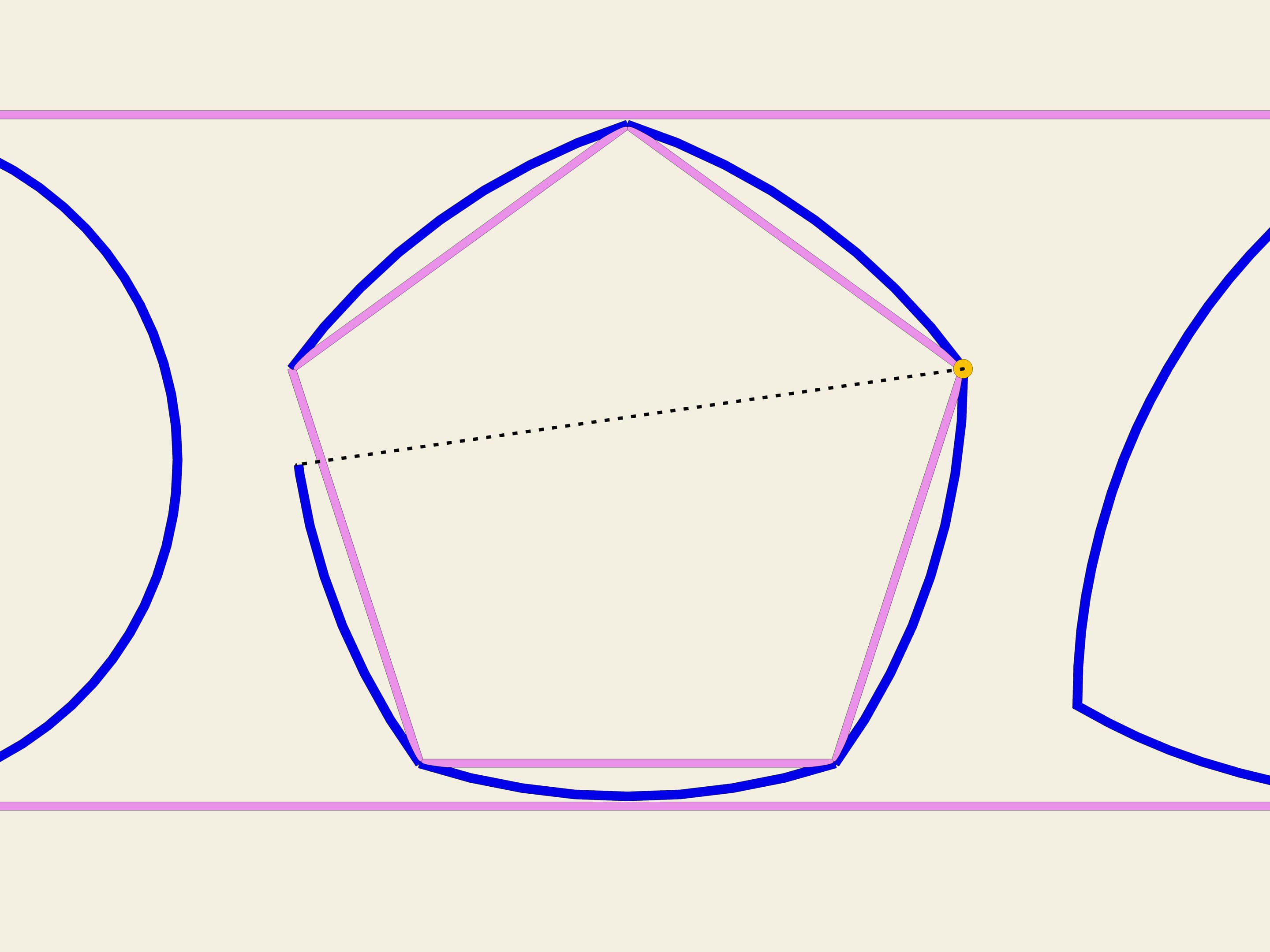
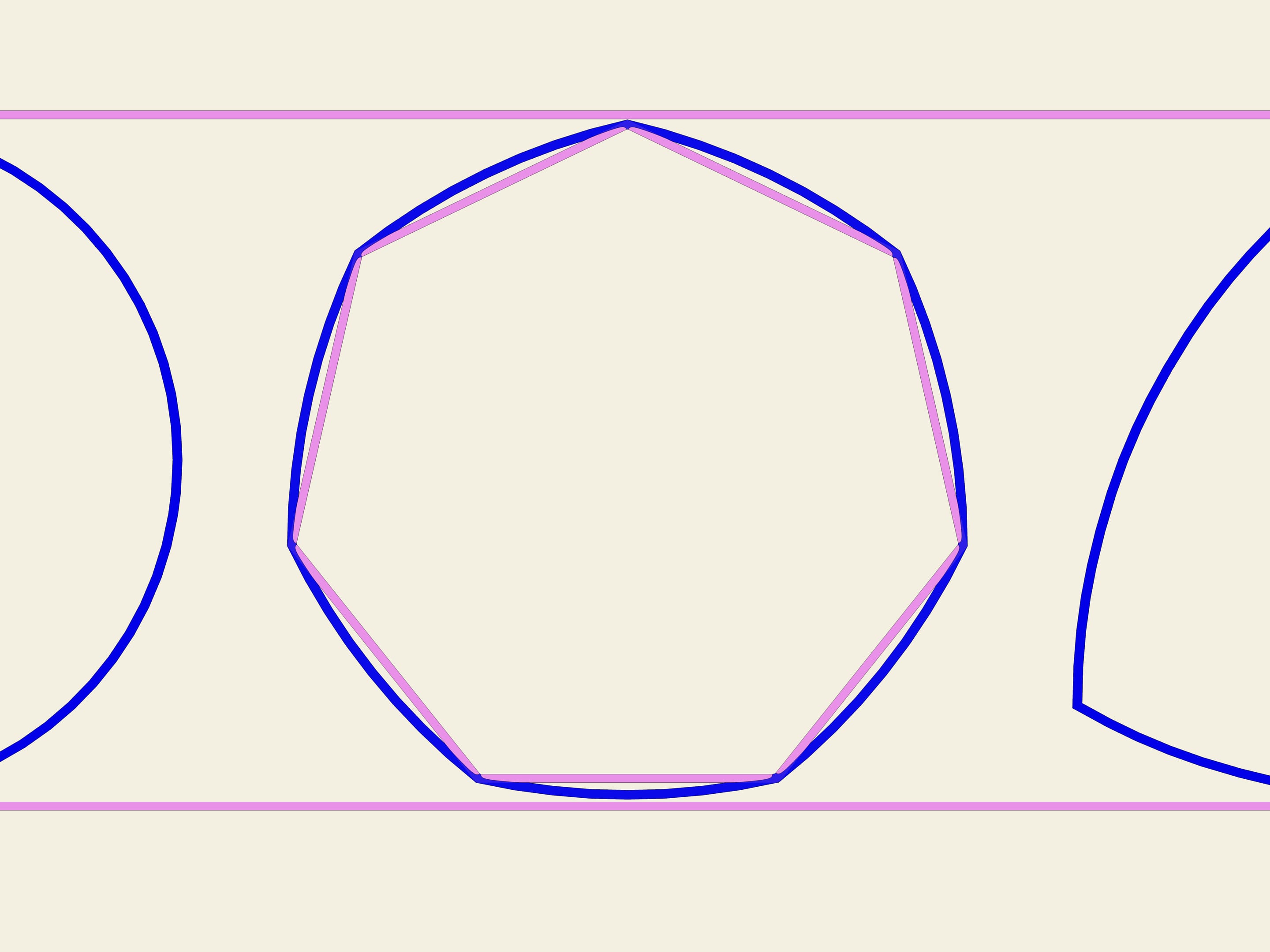
On any regular polygon with odd numbers of vertices it is possible to plot constant width curve according to the scheme that Relo triangle has been constructed. It is necessary to draw an arc of a circle joining endpoints of the opposite side and of center in each vertex. In England 20-pence coin has the form of a constant width curve constructed on a septangle.
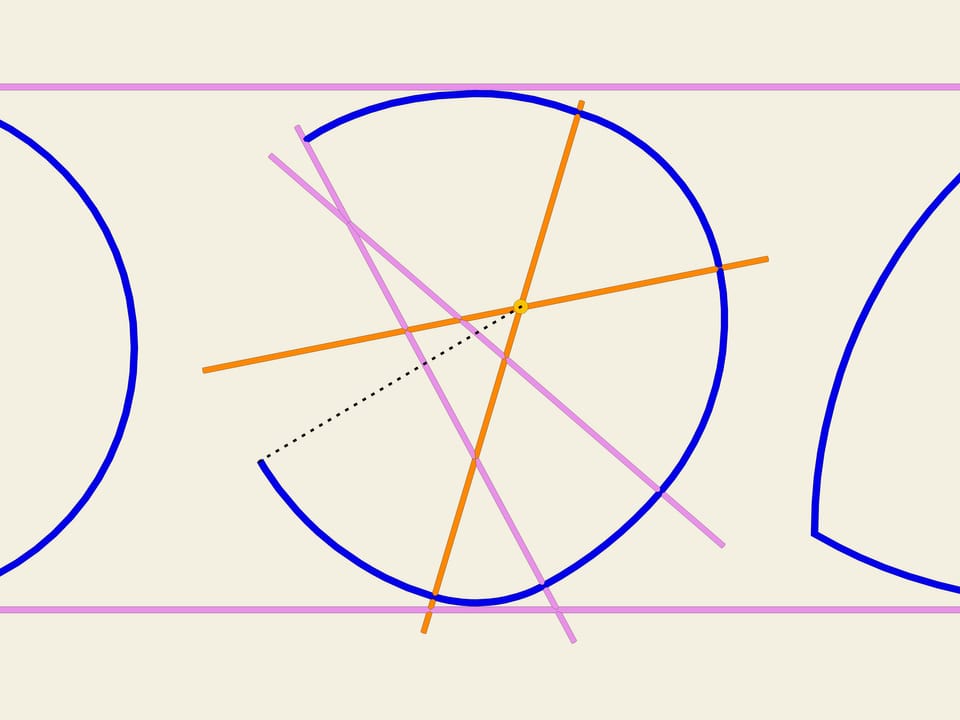
Considered curves do not settle the whole class of curves of constant width. It appears that there exist non-symmetric curves of constant width. We regard arbitrary collection of intersecting lines. Then we regard one of the sectors. We shall draw an arc of a circle of center in the point of intersection of lines, defining this sector, and random radius. Then we shall consider the next sector and we shall draw a circle of center in the point of intersection of lines, bounding this sector. Radius is chosen so that the part of curve, already drawn, can be continuously extended. We shall proceed further our construction.It turns out that the curve will close and we will obtain a constant width curve. Prove it
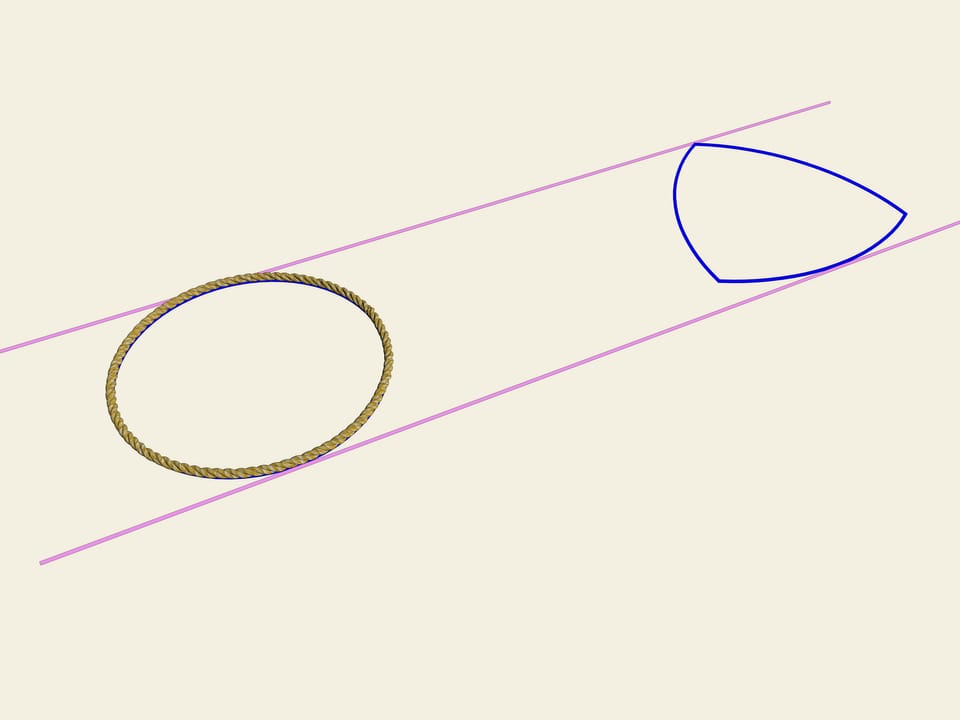
All curves of a given width have equal perimeters. The circle and Reuleaux triangle stand out from all rest curves of a given width with its extreme properties. The circle bounds the largest area and Reuleaux triangle — the least one.
Reuleaux triangle is often studied at mathematical circles. It appears that this geometrical figure has interesting applications in mechanic.
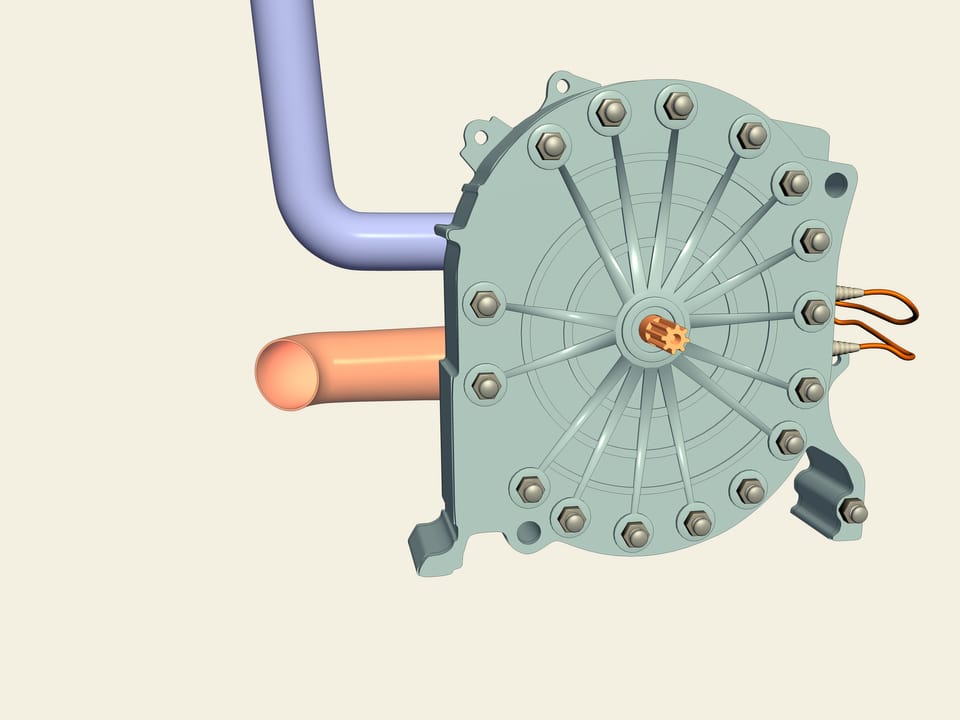
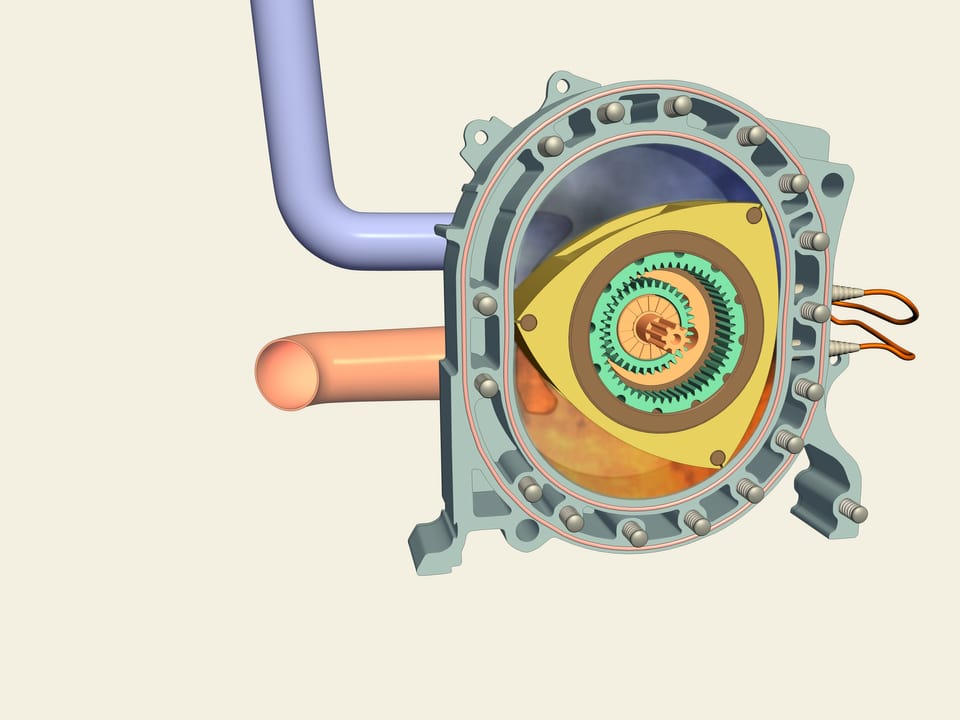
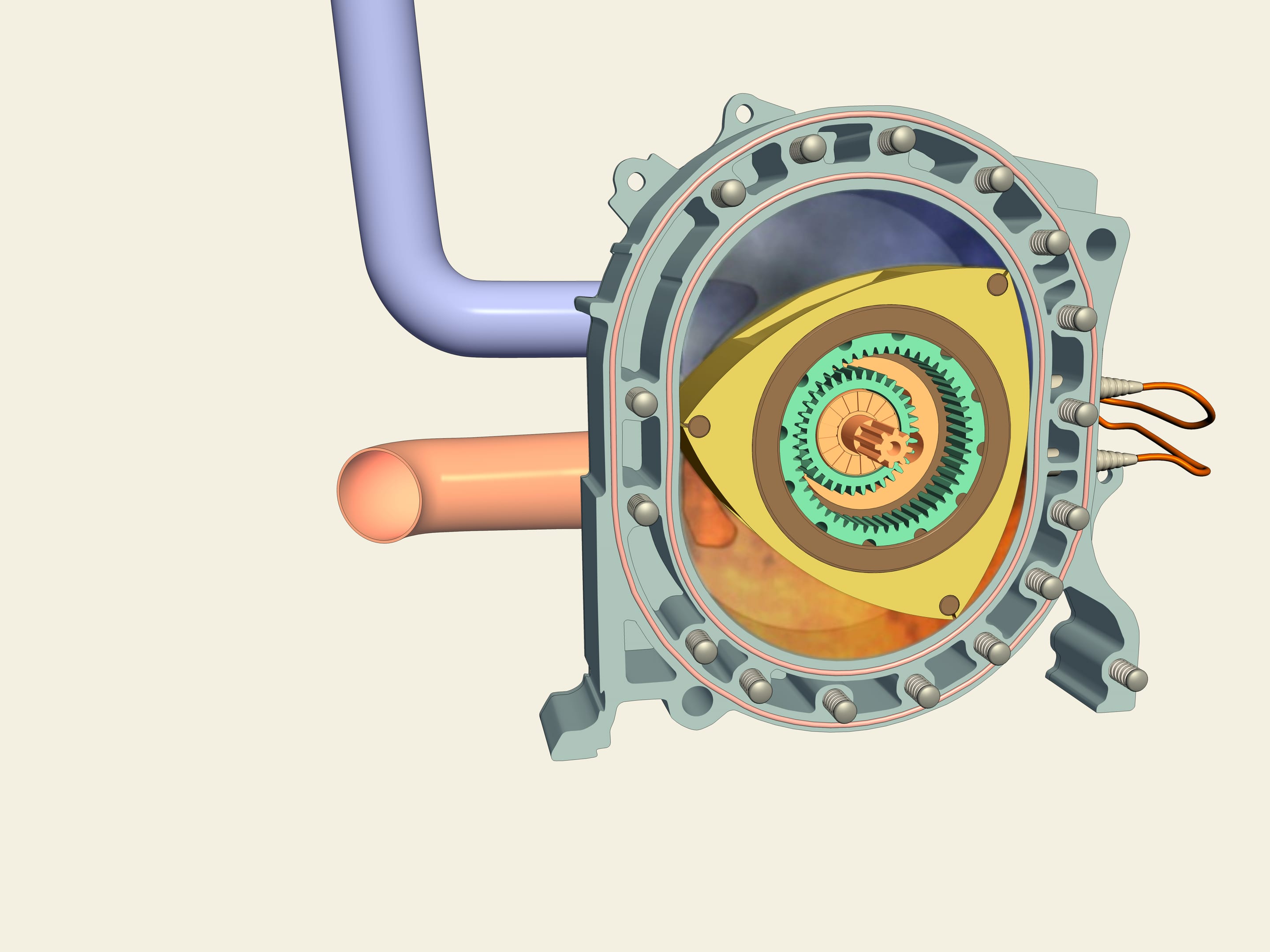
Look, it is Mazda RX-7. Unlike the majority of serial cars it (and also model RX-8) is equipped with rotary engine of Vankel. How is it constructed? It is Reuleaux triangle that is used as a rotor! Rotor separates a chamber into three parts, each become combustion chamber by turns. At first a dark blue air-fuel mixture is injected, then because of movement of rotor it is compressed, fired and twists a rotor. A rotary engine is void of some lacks of free-piston engine. For instance, here rotation is transmitted directly to an axis and it is not necessary to use crankshaft.
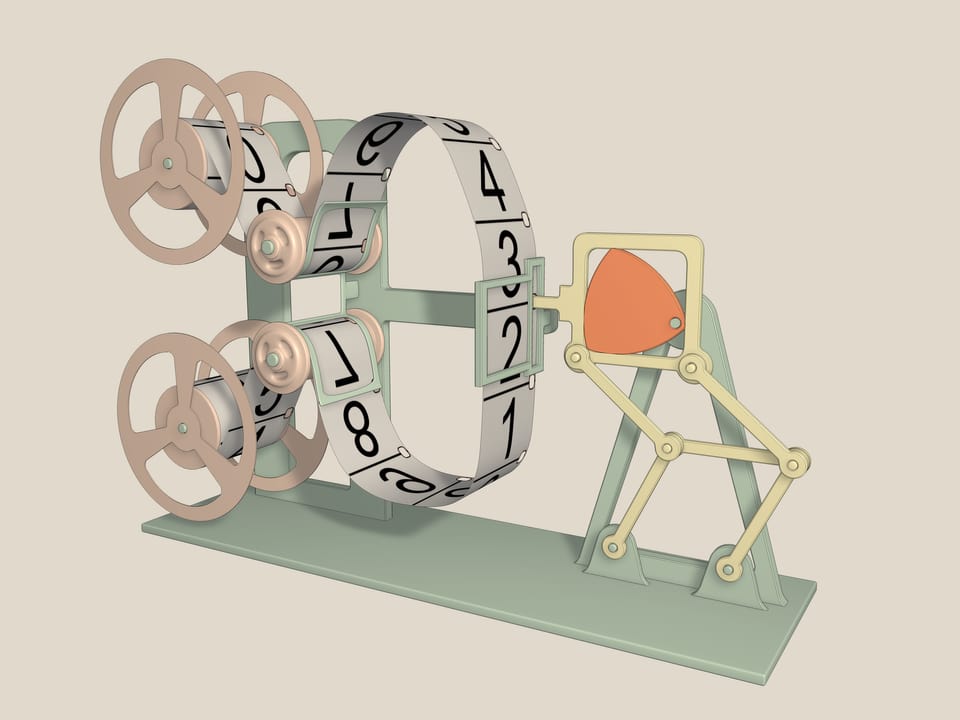
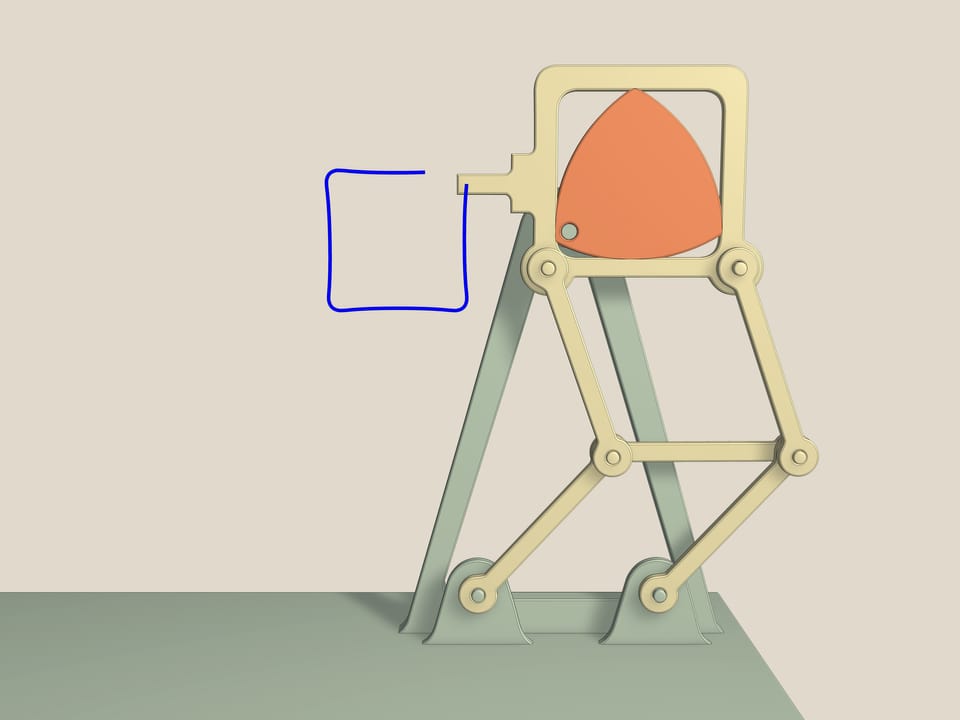
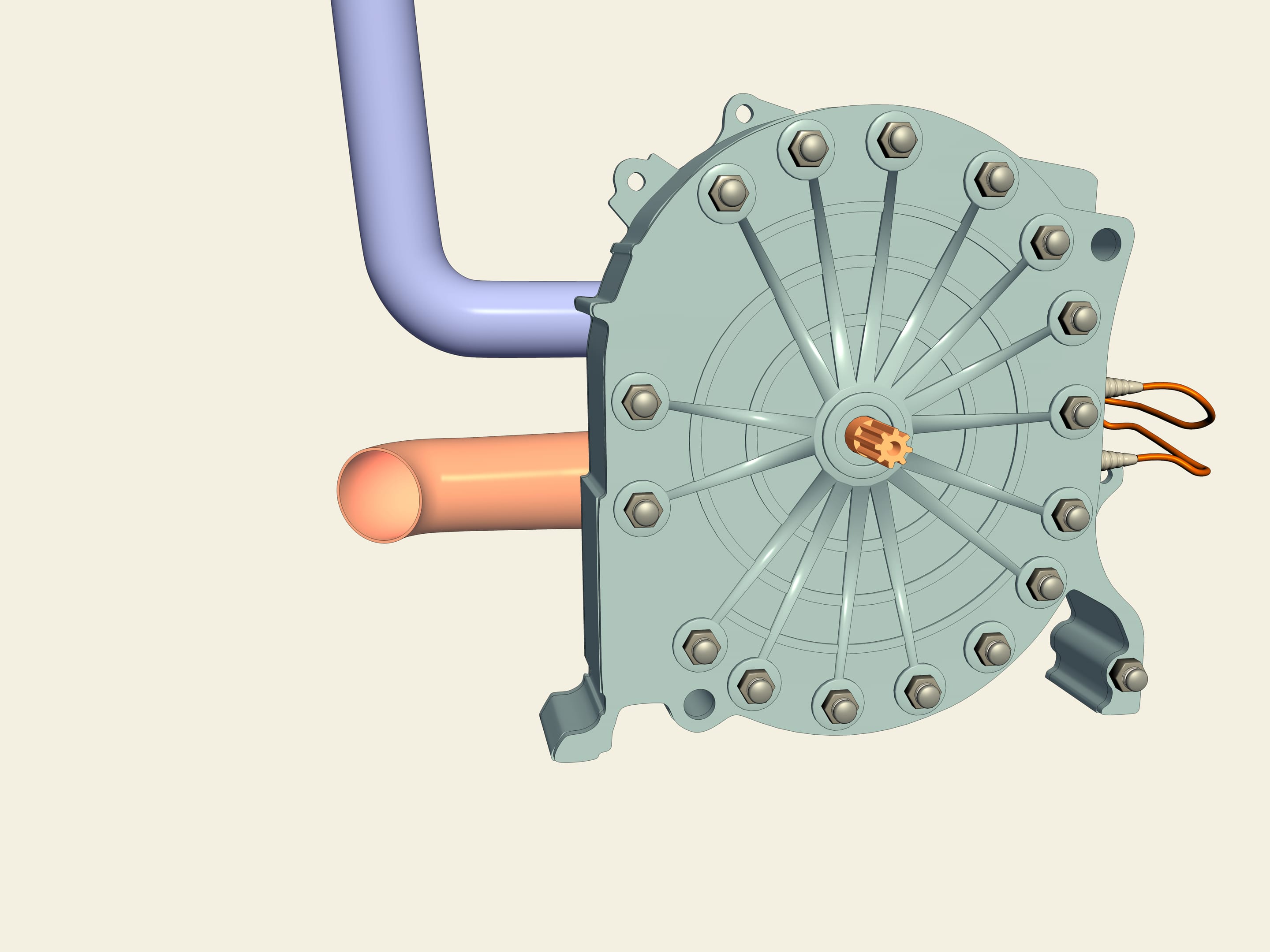
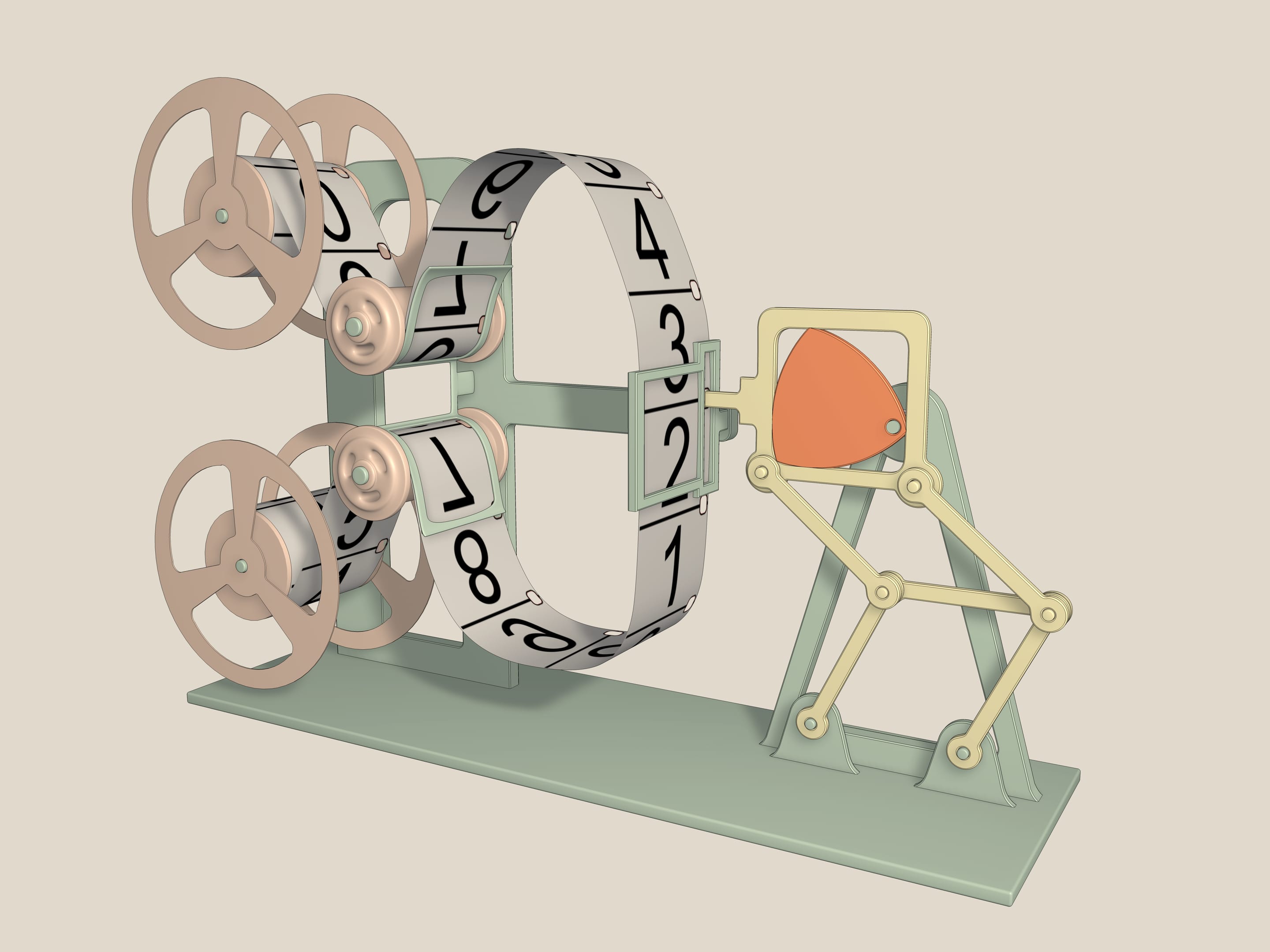
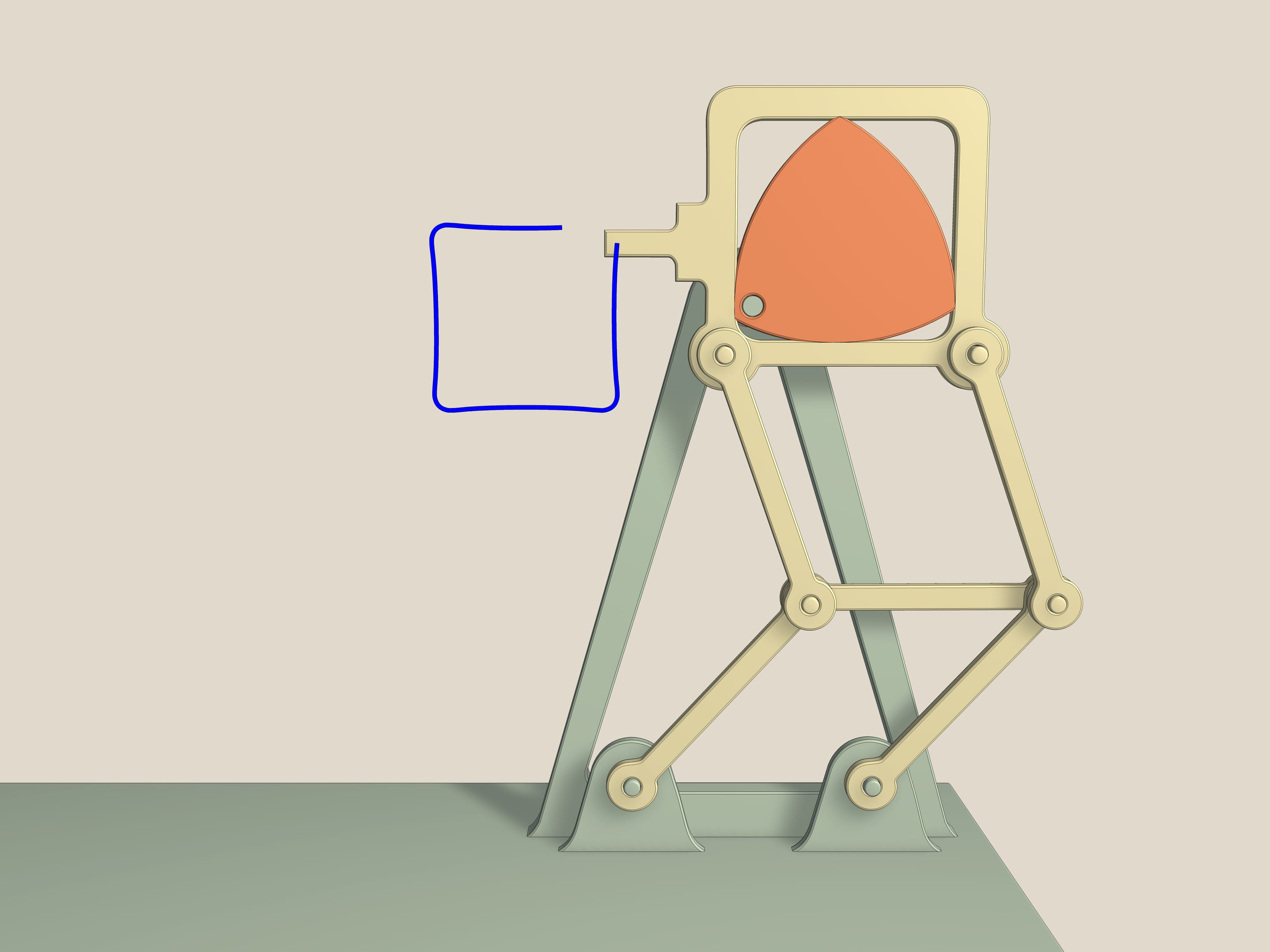
And this is claw mechanism. It was used in film projectors. Engines give uniform rotation of an axis. But for a sharp image, it is necessary to pull a film for one frame, to stop it, and then again to pull quickly. And so 18 times per second. The claw mechanism solves this problem. It is based on Reuleaux triangle inscribed into a square and two parallelograms, which prevent his deviations. Indeed, since the lengths of the opposite sides are equal, then the middle section, the base, and the side of the square are always parallel to each other. The closer the axis of clamping to the vertex of Reuleaux triangle the closer the figure described by dentical of claw device to a square.
And that is that one would think purely mathematical problems find interesting applications.