Since James Watt invented the steam engine there has been a problem to build a hinge mechanism that transform circular motion to linear.
A great Russian mathematician Pafnutiy Lvovich Tchebyshev couldn't solve the initial problem, but investigating it he developed a theory of approximation and of mechanism synthesis. Applying the latter he could choose the parameters of a lambda-mechanism so that… Well, we'll talk about it below.
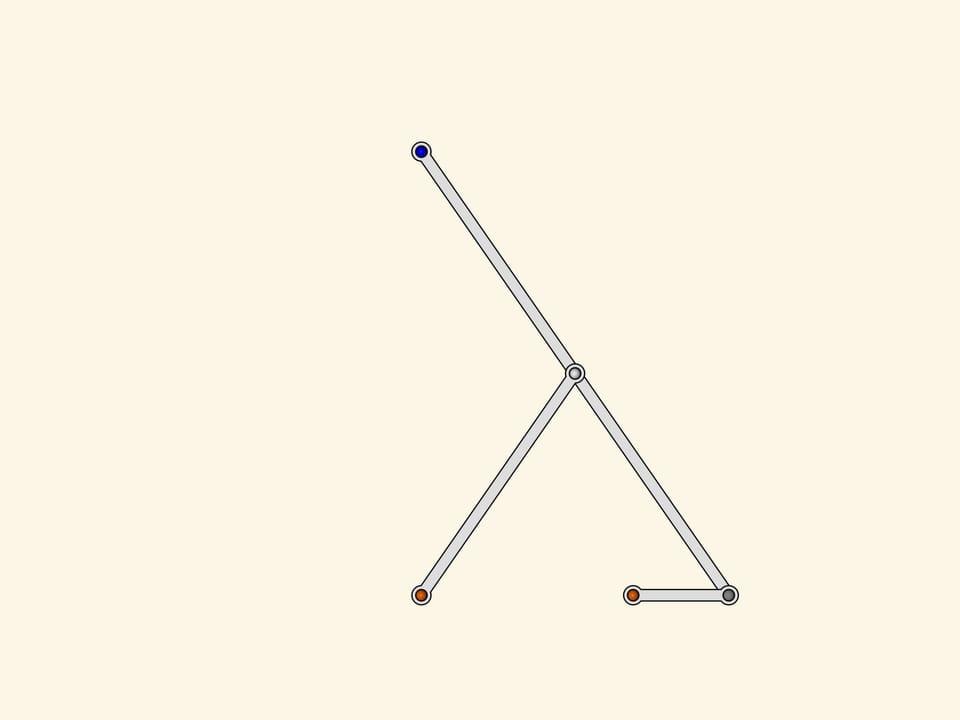
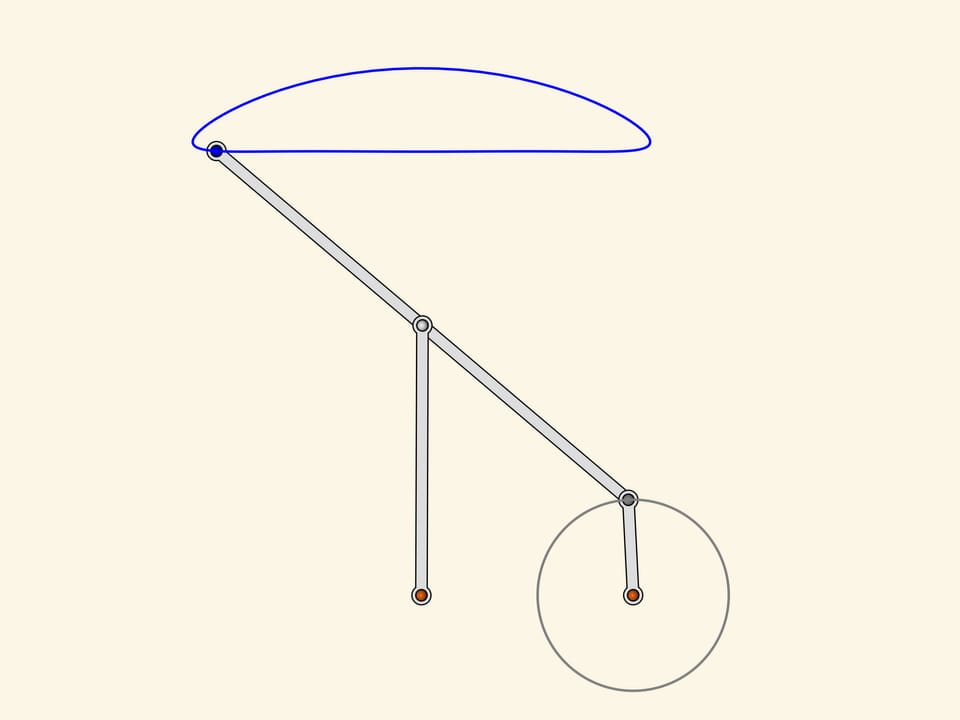
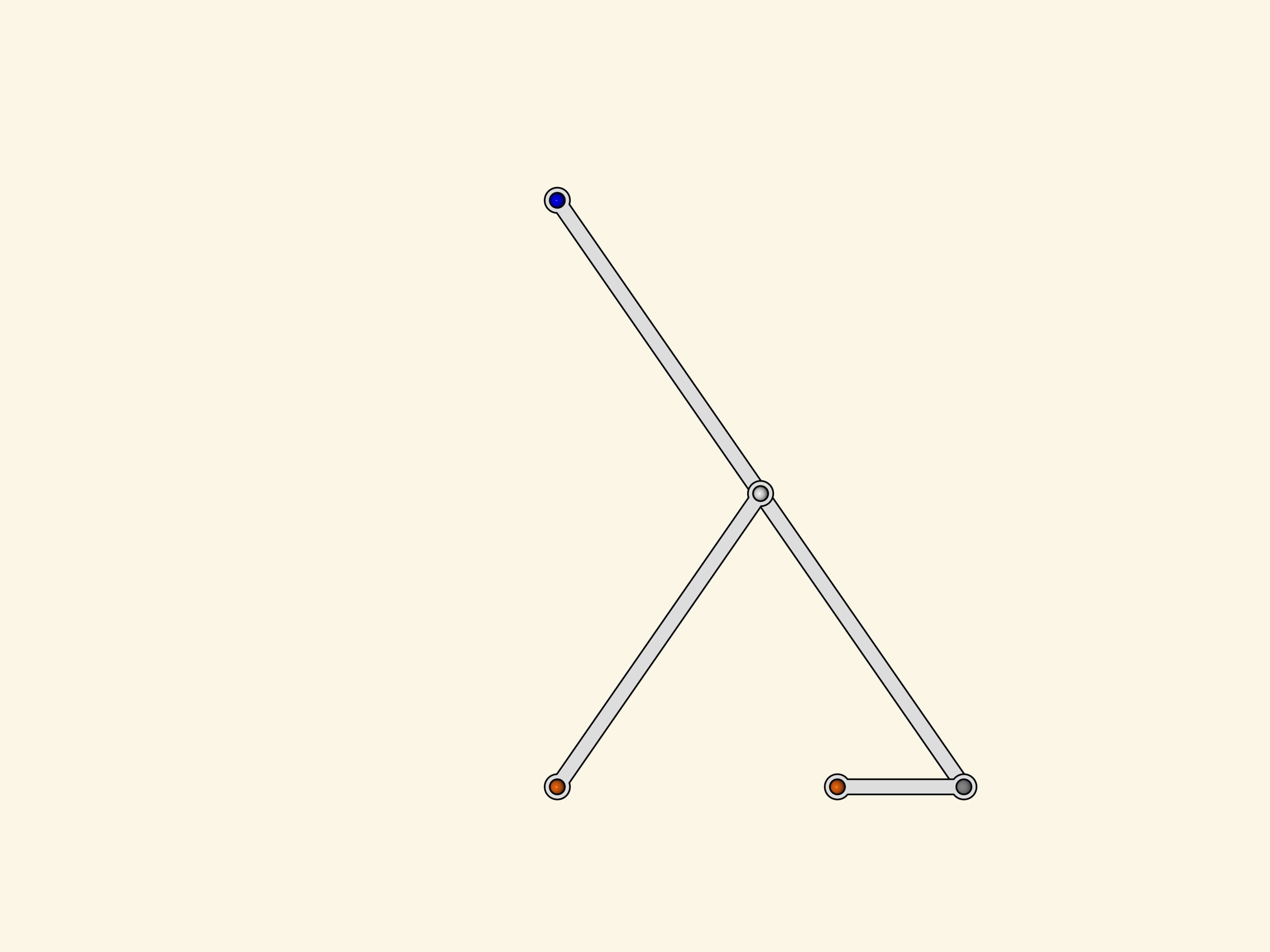
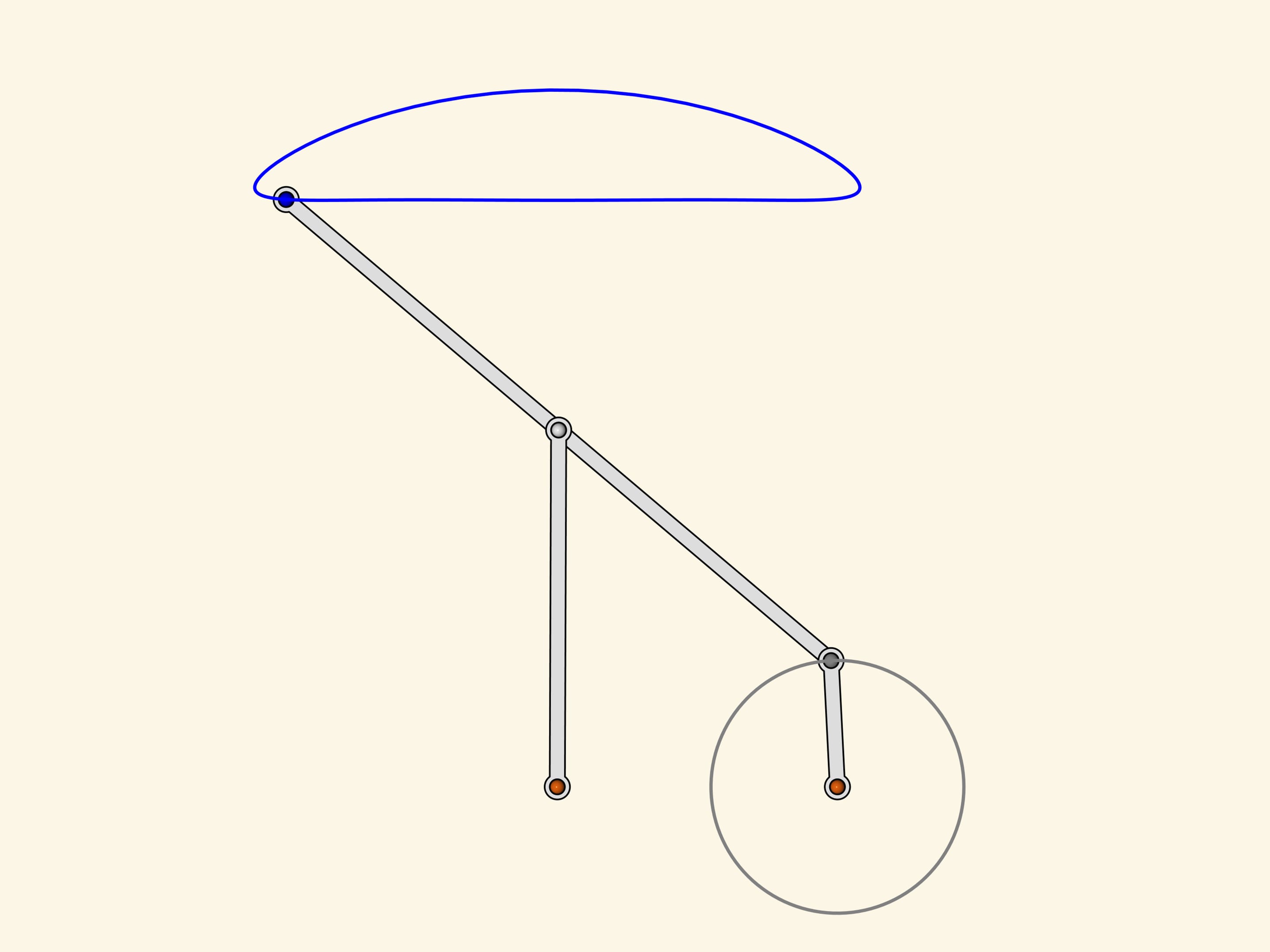
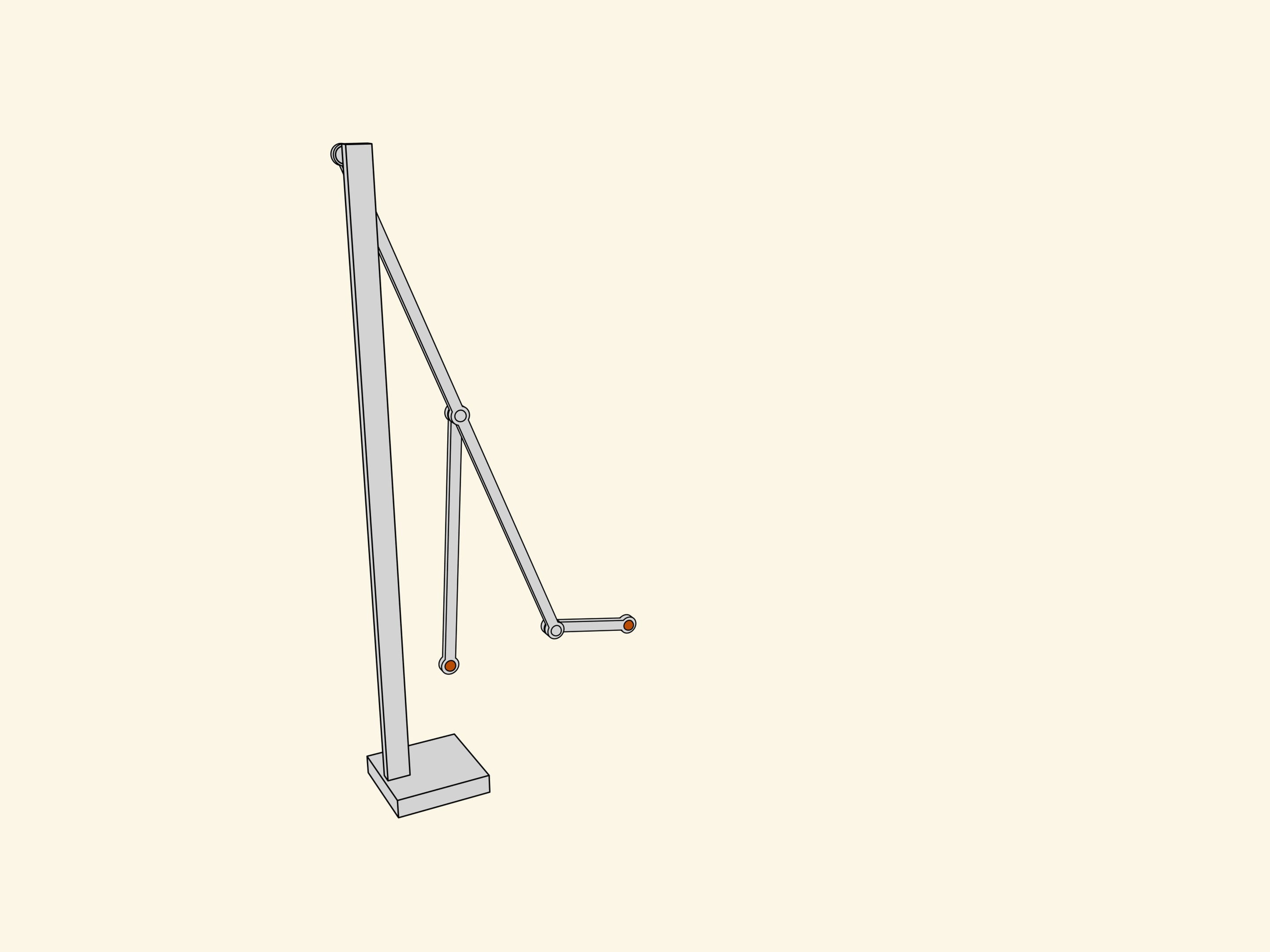
Two fixed red hinges, three edges of the same length. As it looks like the greek letter lambda, this mechanism was named after it. The loose gray hinge of the little driving edge turns around forming a circle while the slave blue hinge has a trajectory that looks like a mushroom's cap.
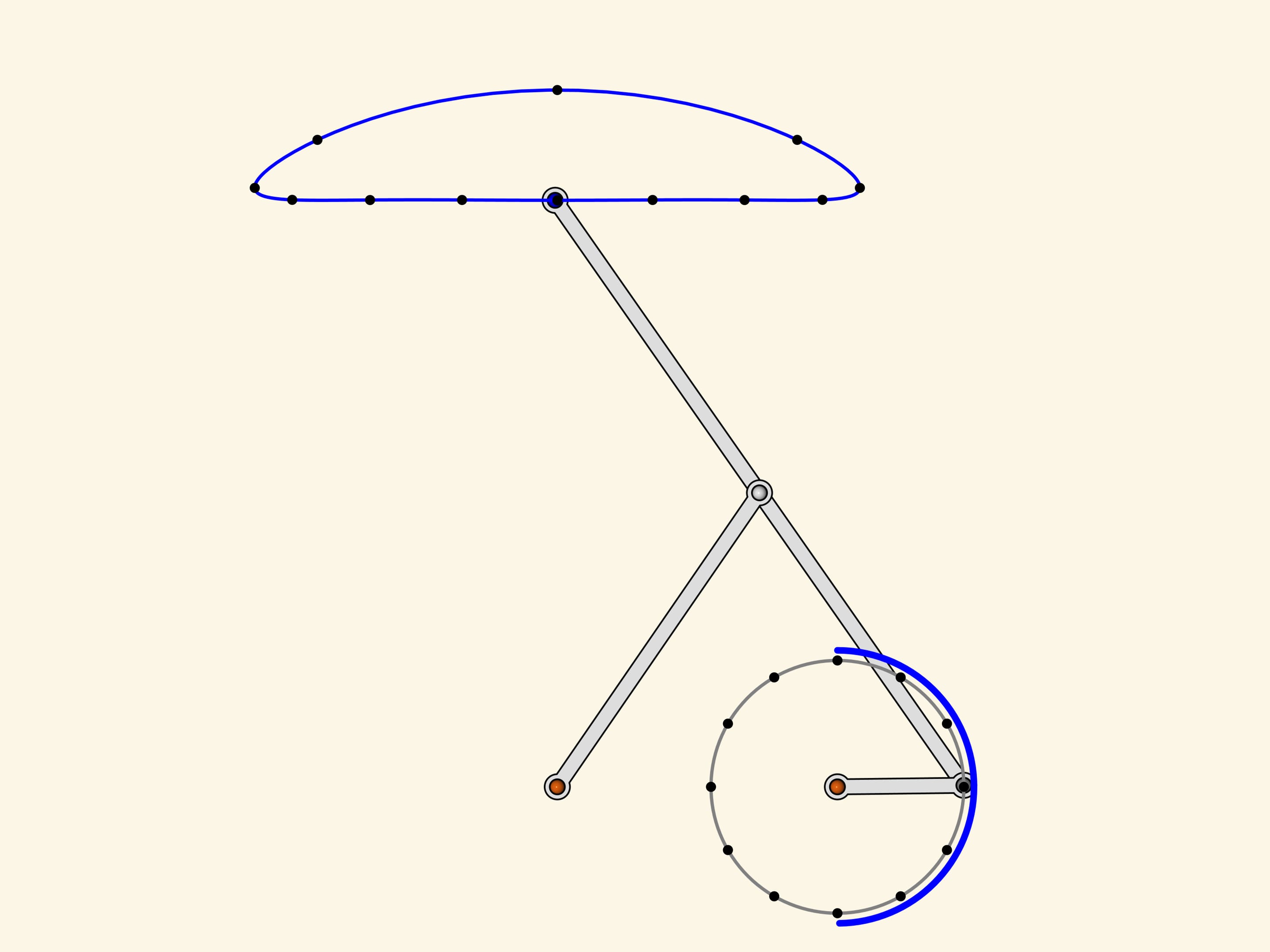
Put on the circle of the driving hinge marks at regular intervals and the corresponding marks on the trajectory of the slave one.
The lower part of the «cap» corresponds exactly to a half of the period of the driving hinge's motion. At the same time, the lower part of the blue curve doesn't differ much from a straight linear motion (the difference is less that a percent of the short driving edge length).
What else does this blue trajectory look like? Pafnutiy Lvovich could see similarity with the horse hoof's motion trajectory!
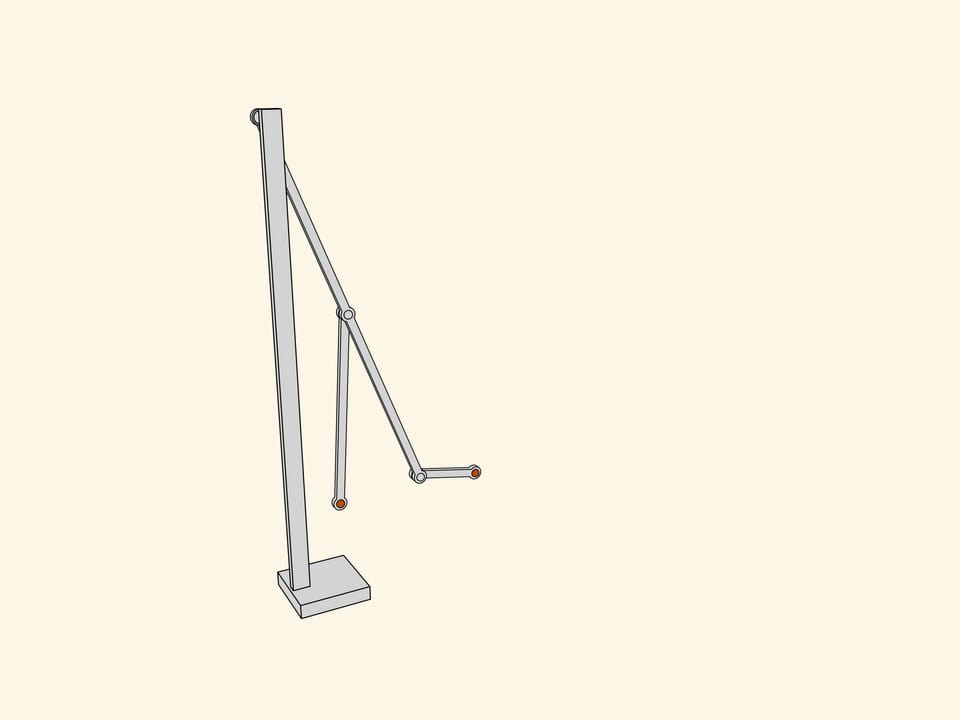
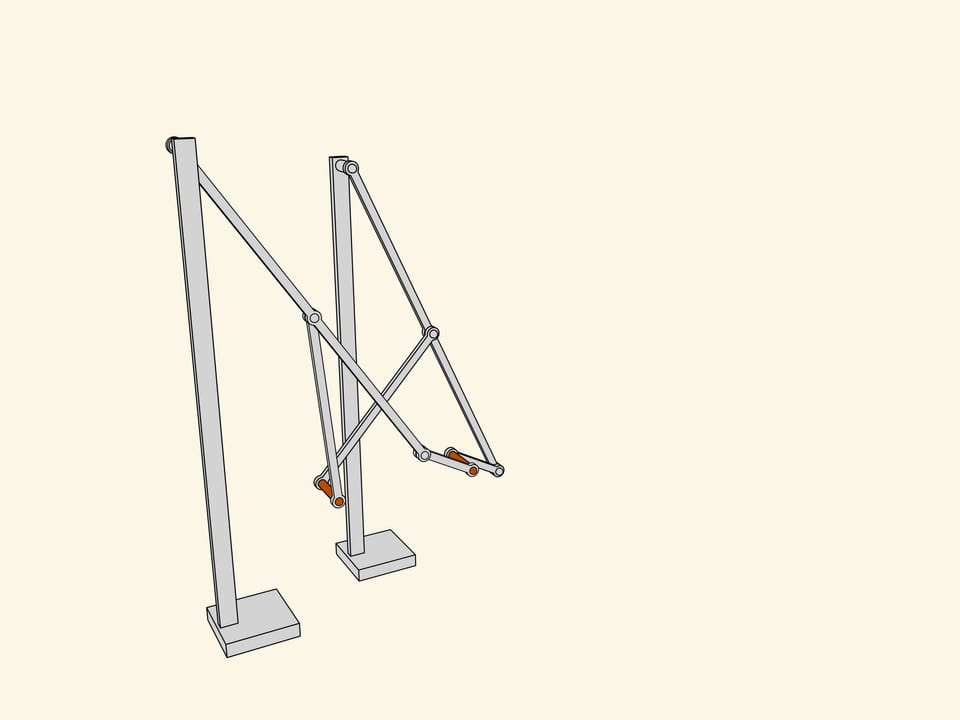
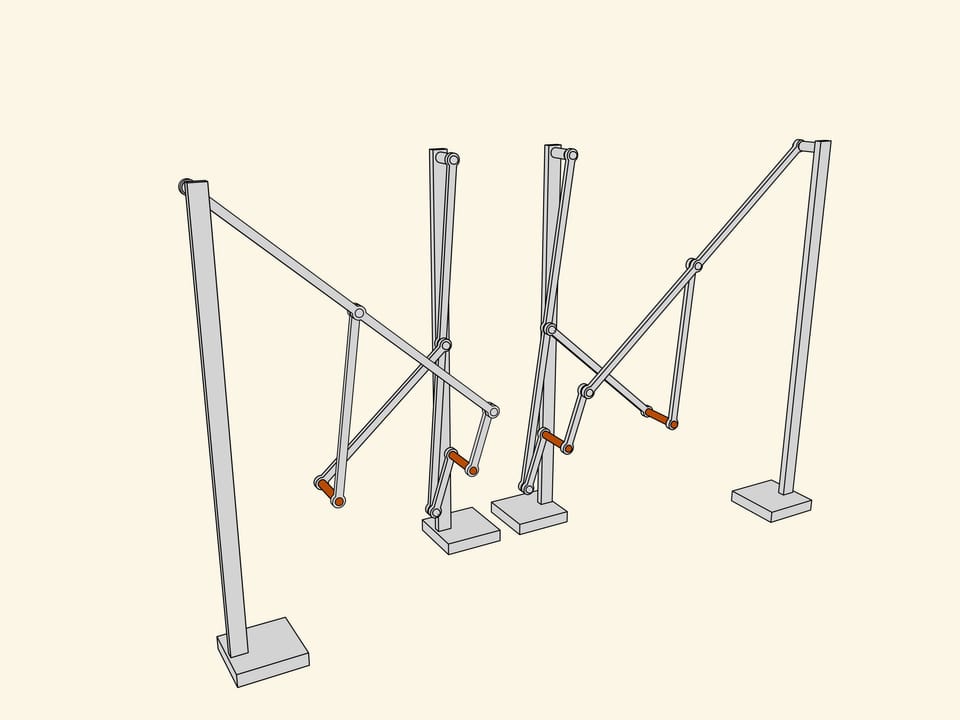
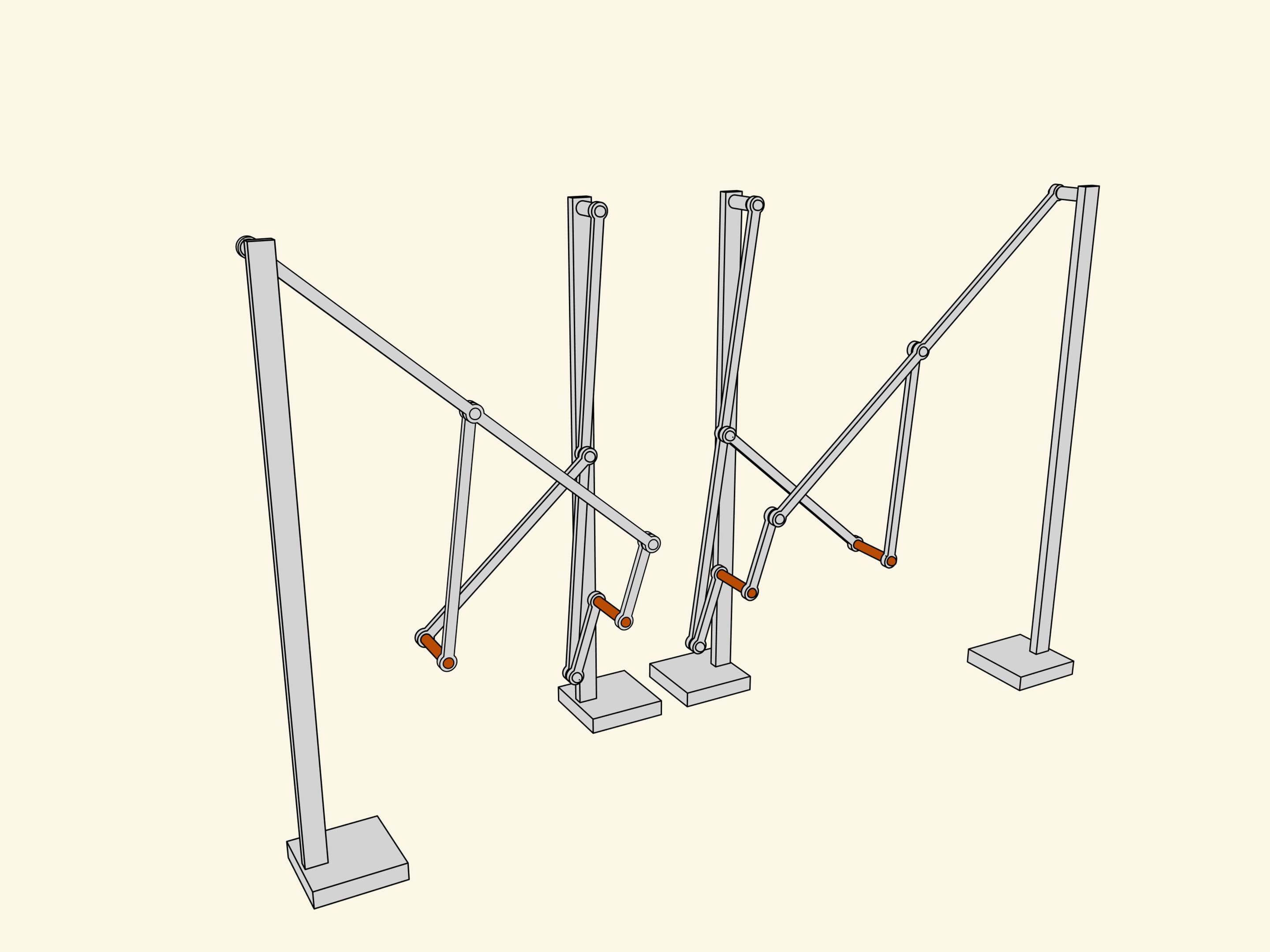
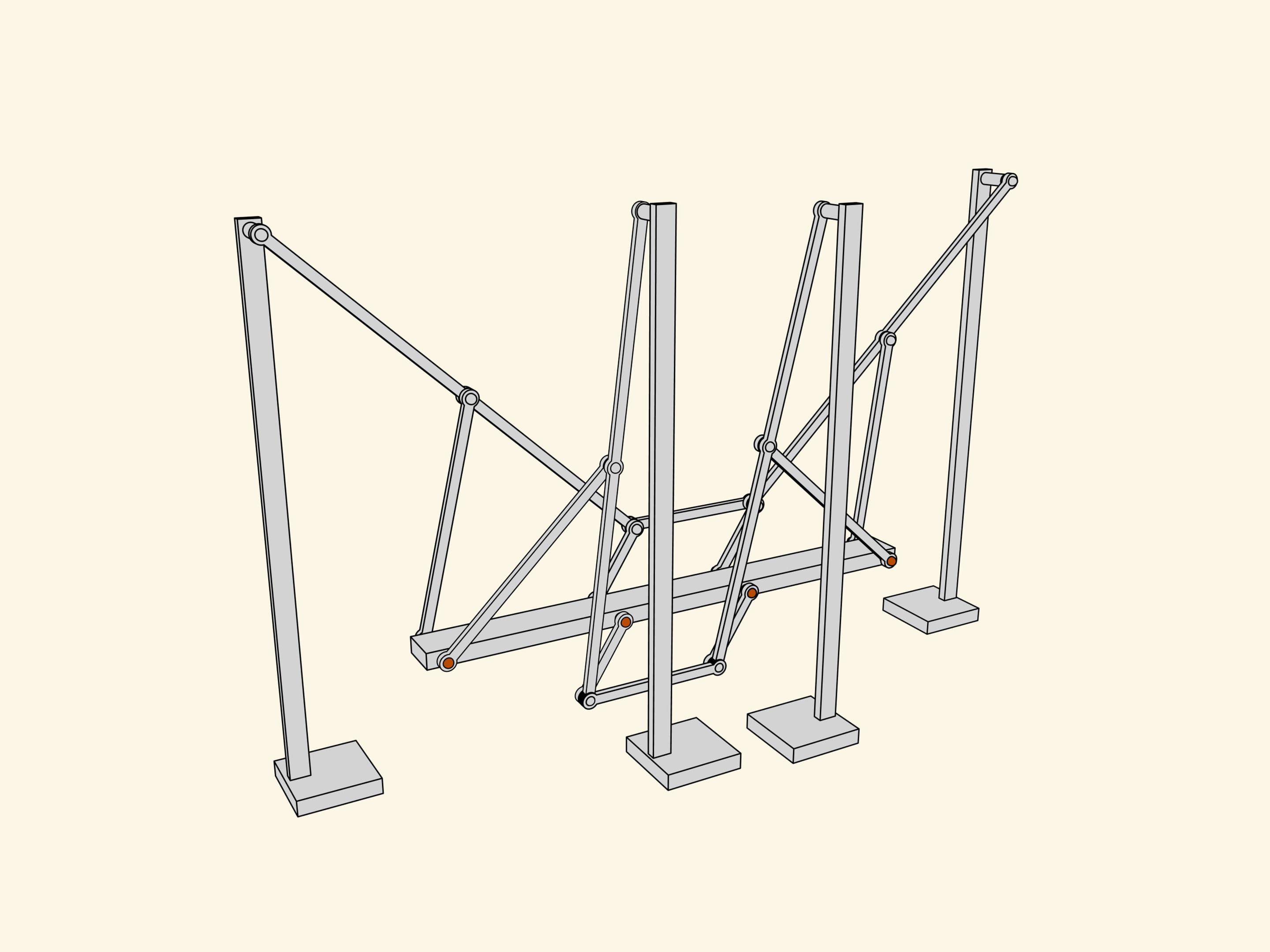
Let's attach a mirror copy of the two-leg part we've already made. Additional links coordinate the phases of rotation and a common platform connects the axes. As they say in mechanics, we've got a kinematical scheme of the first walking machine in the world.
Being a professor in Saint-Petersburg university, Pafnutiy Lvovich spent most part of his salary on construction of the mechanisms he invented. He built the described one «in wood and steel» and called it a «Plantigrade machine». The first walking machine in the world invented by a Russian mathematician was greatly approved during the Wold exhibition in Paris, 1878.
Thanks to the Polytechnical museum of Moscow that preserved the Tchebyshev's original and let «Mathematical etudes» measure it, we have an opportunity to see in action an exact 3D-model of a plantigrade machine of Pafnutiy Lvovich Tchebyshev.