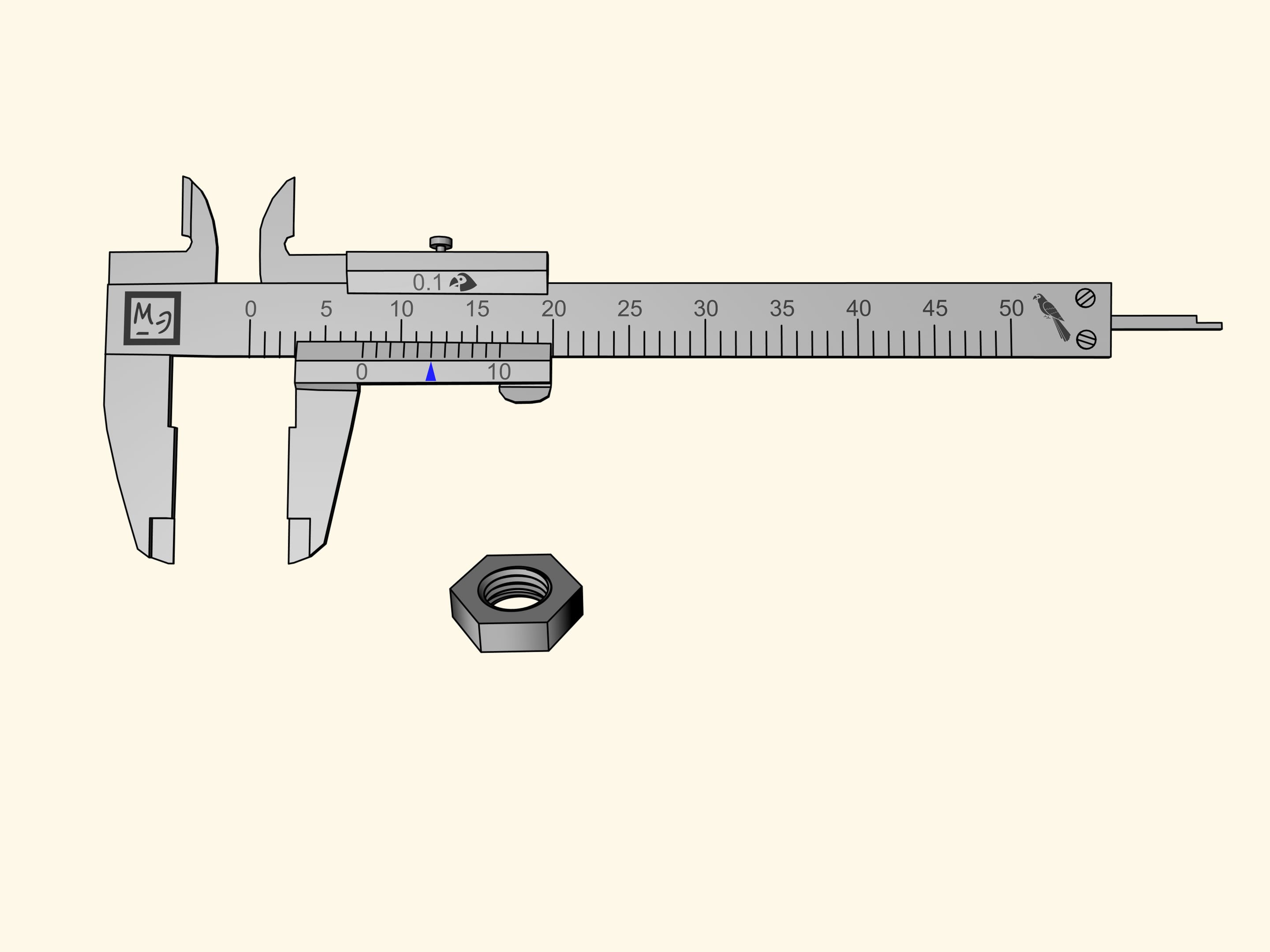
We will make measurements of lengths . But, before measuring something, one should always define the units in which the measurements are made. The Russian guys remember a song that said: “But in ’parrots’ I am much taller!”
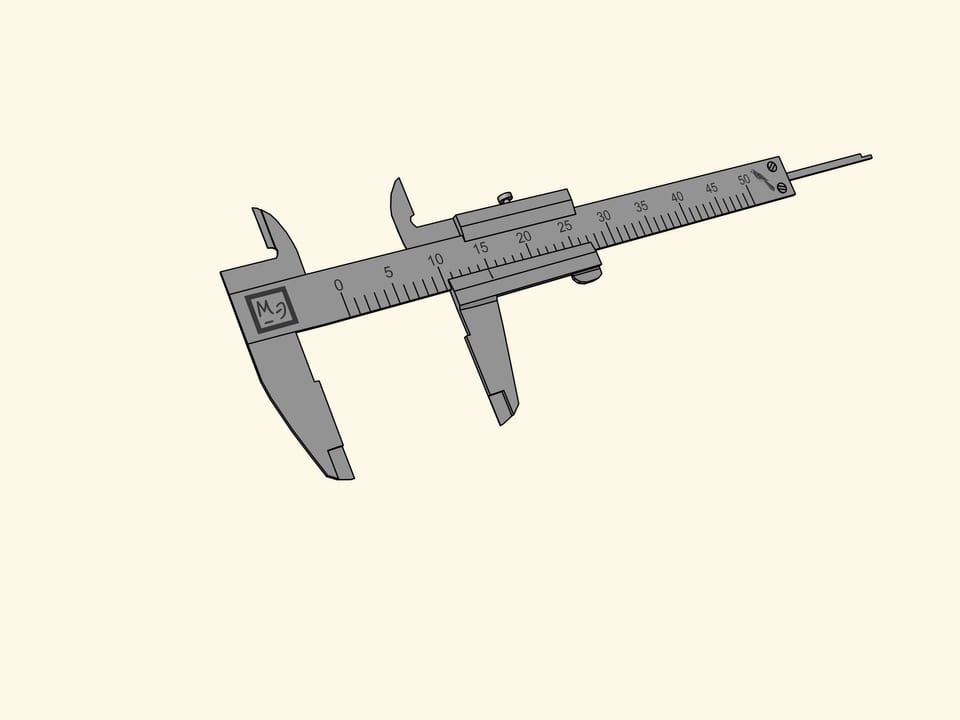
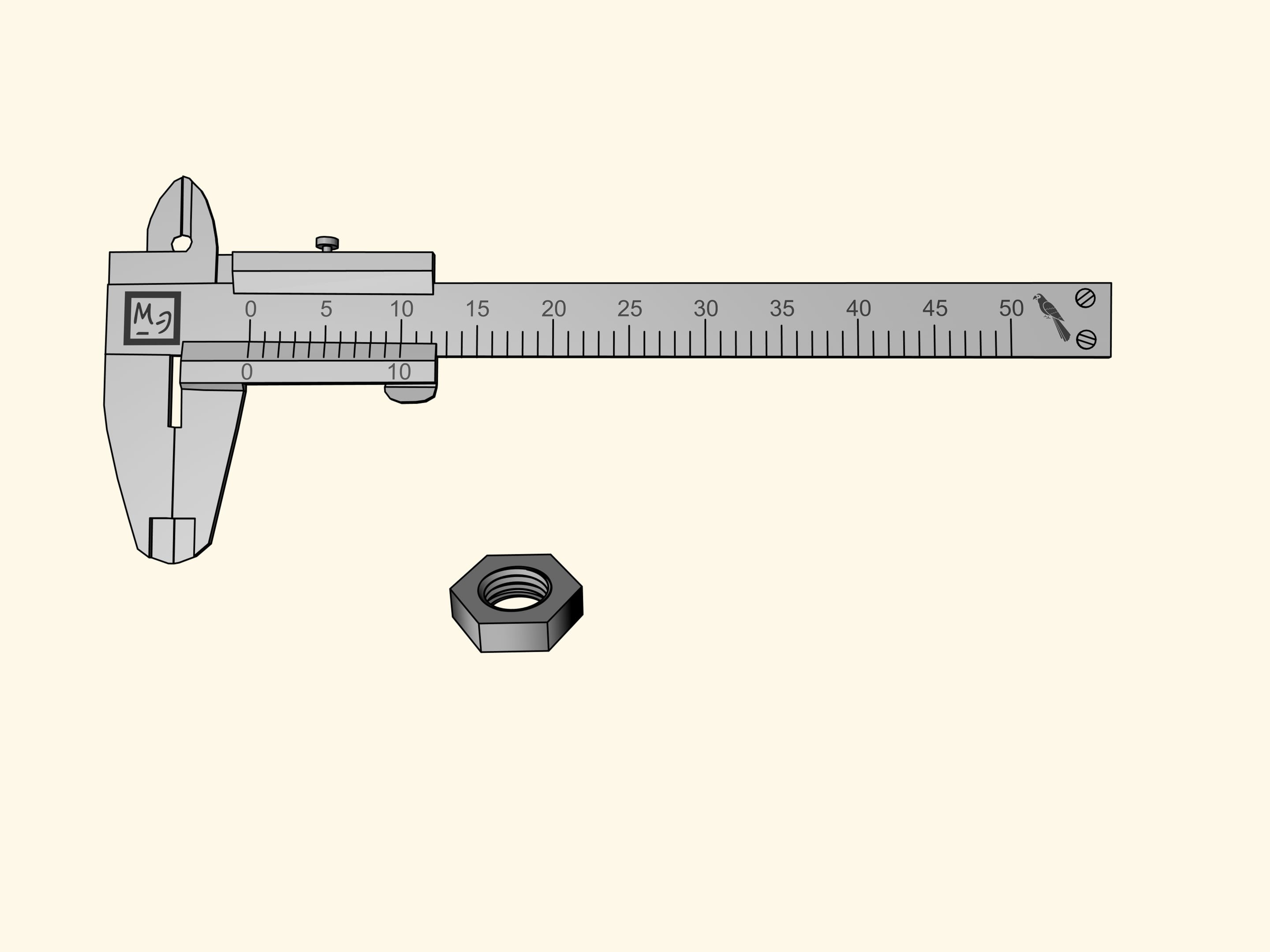
How to measure ’in parrots’ with the calliper? The tips that stick out below the main bar with the rule are used for external measures when one needs to measure, for example, the outer diameter of a tube. The tips for the inner measures, used to measure, for instance, the inner diameter of a tube, stick out over the bar. Finally, there is a ’tail’ that protrudes at the end of the bar, and serves to measure the depth, for example, of a hole. These three parts are fixed to a sliding bar measuring 15 parrots.
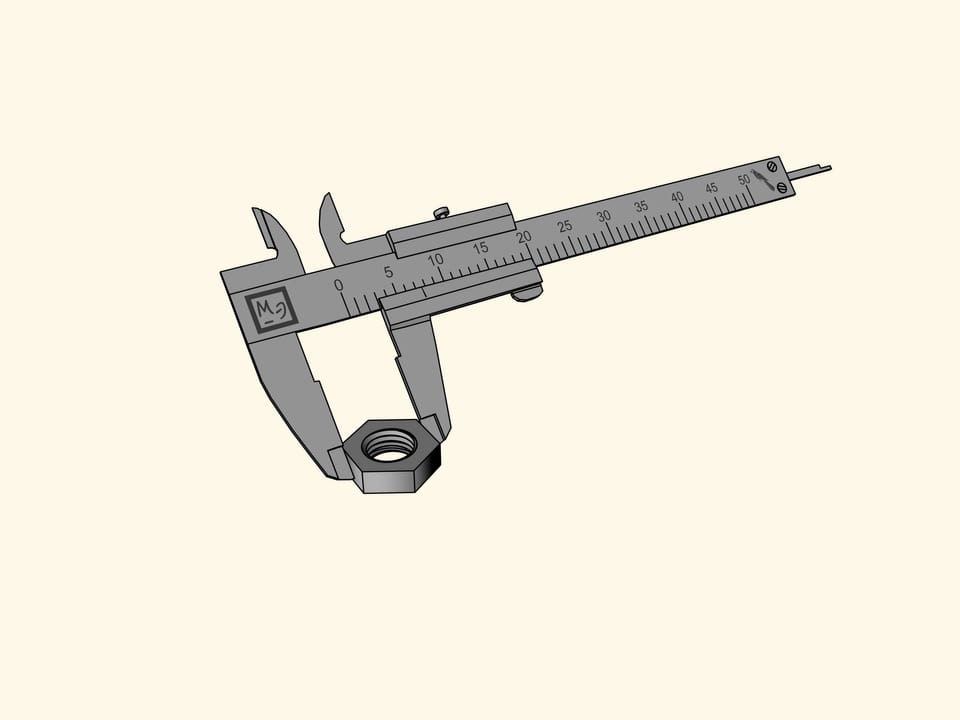
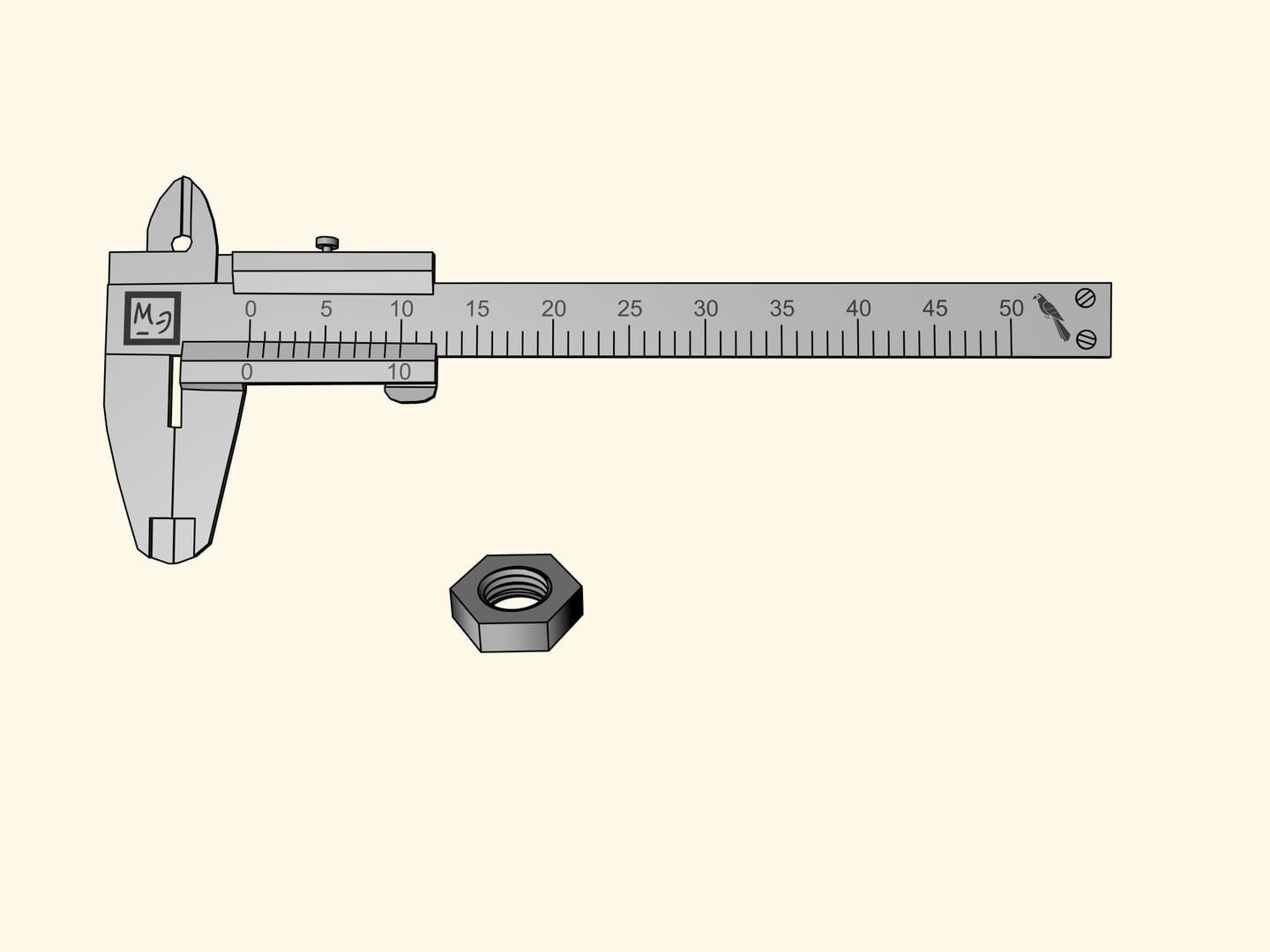
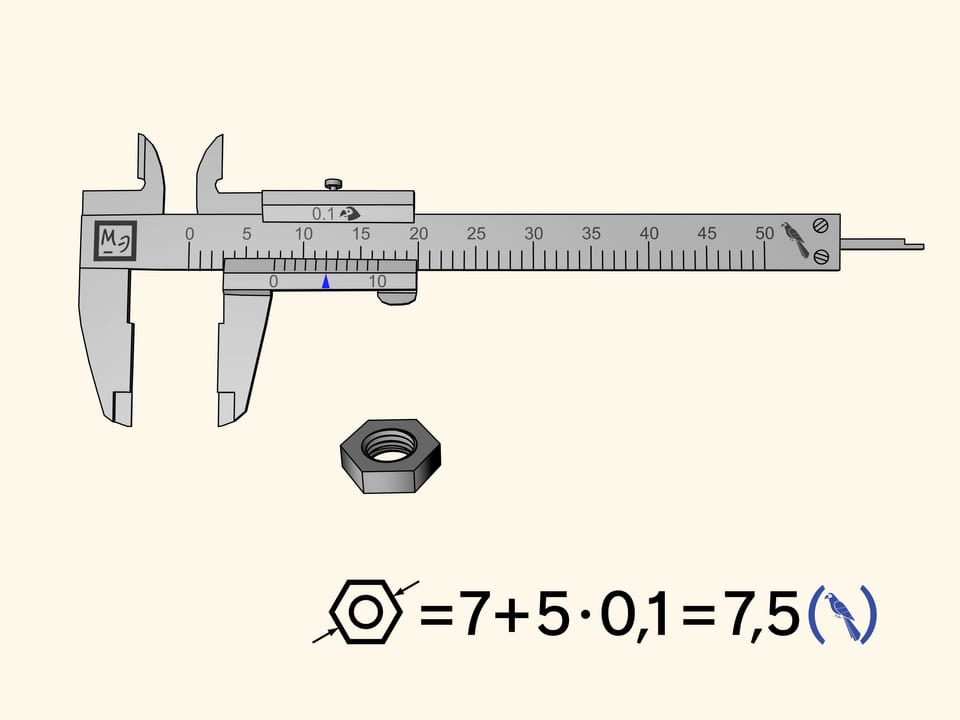
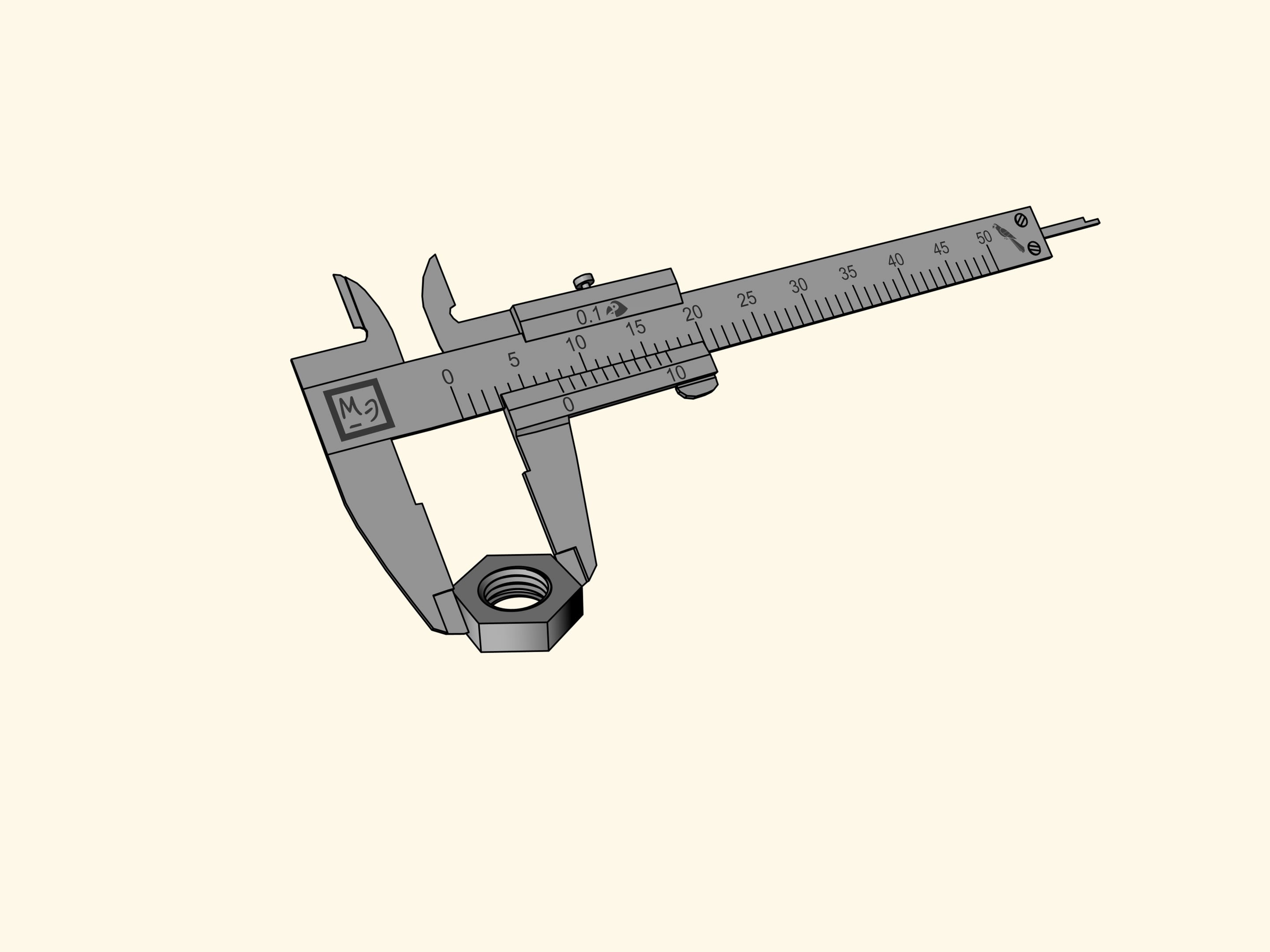
Let us measure a hexagonal lock nut. Unfortunately, the reference nick of the sliding bar showing the size of the nut, falls between two divisions of the main rule. This measure allows us to say only that the nut measures more than seven parrots, but less than eight. It is difficult to define its size more precisely by eye.
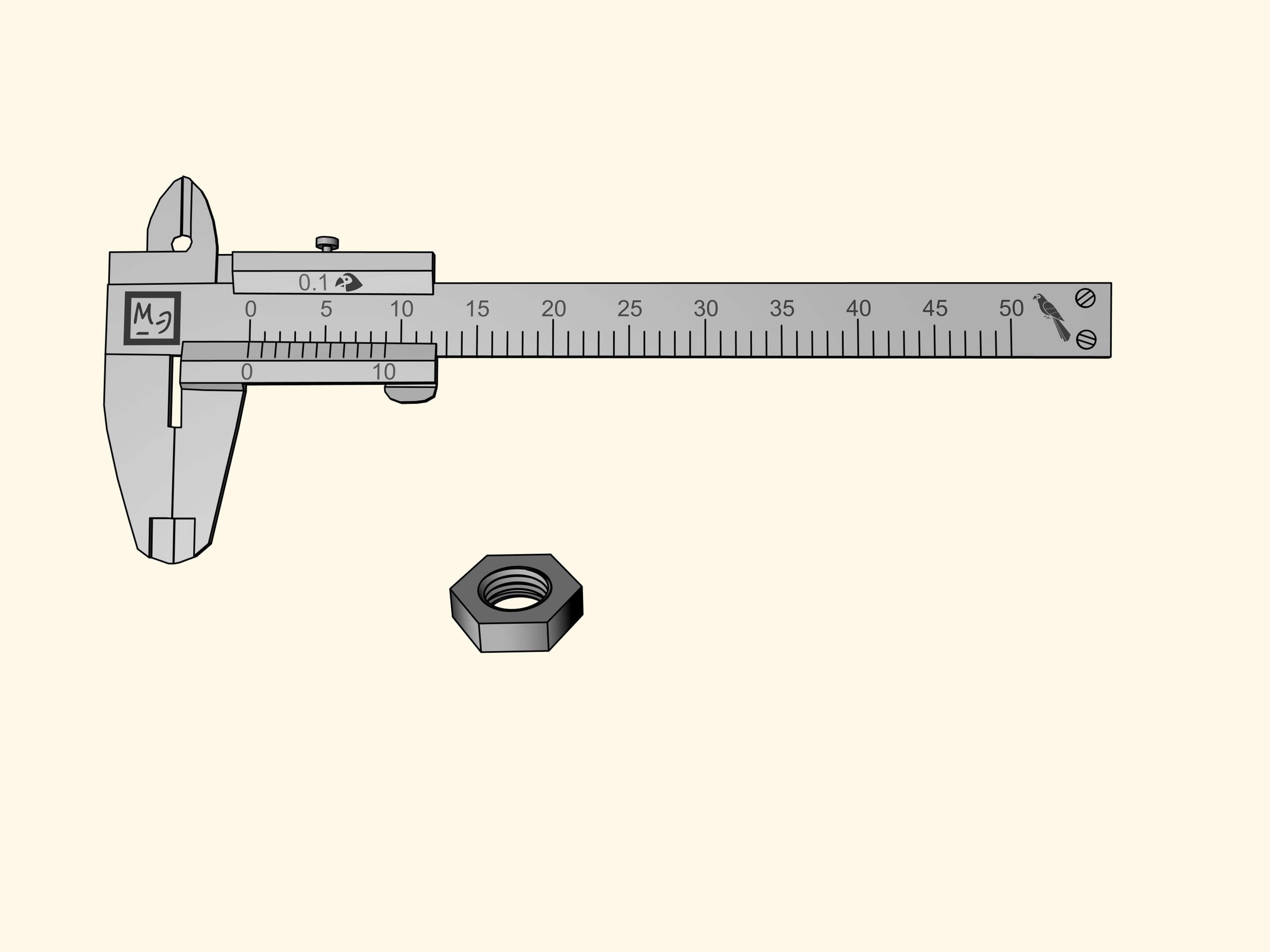
One method, which do not complicate at all the construction of the same calliper, but allows to do more accurate measures, was invented a few centuries ago. This only adds on the moving bar a new graduate scale, the vernier scale.
Let us take on this sliding bar ten nicks after the nick of reference (the zero), that coincide with the nicks between 0 and 10 of the rule. Now compress evenly these ten divisions to occupy nine divisions of the rule. The vernier scale was invented in its modern form in 1631 by the mathematician Pierre Vernier (1580–1637). In some languages, this device is called a nonius. Nonius is the Latin name of the Portuguese astronomer and mathematician Pedro Nunes (1502–1578) who in 1542 invented a similar system.
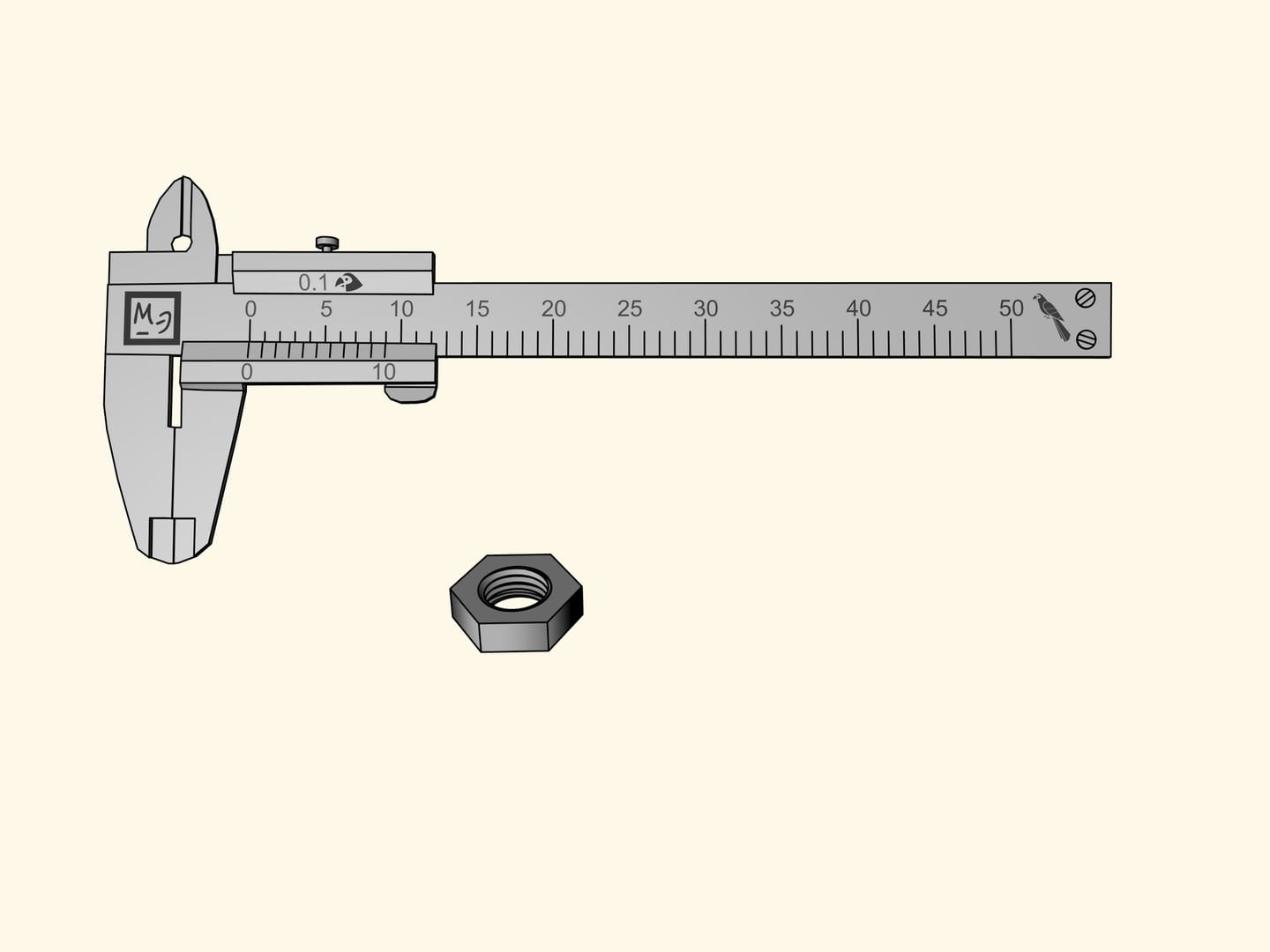
It happens that the additional rule built in this way allows to measure with an accuracy of $0{.}1$ parrots. But how?
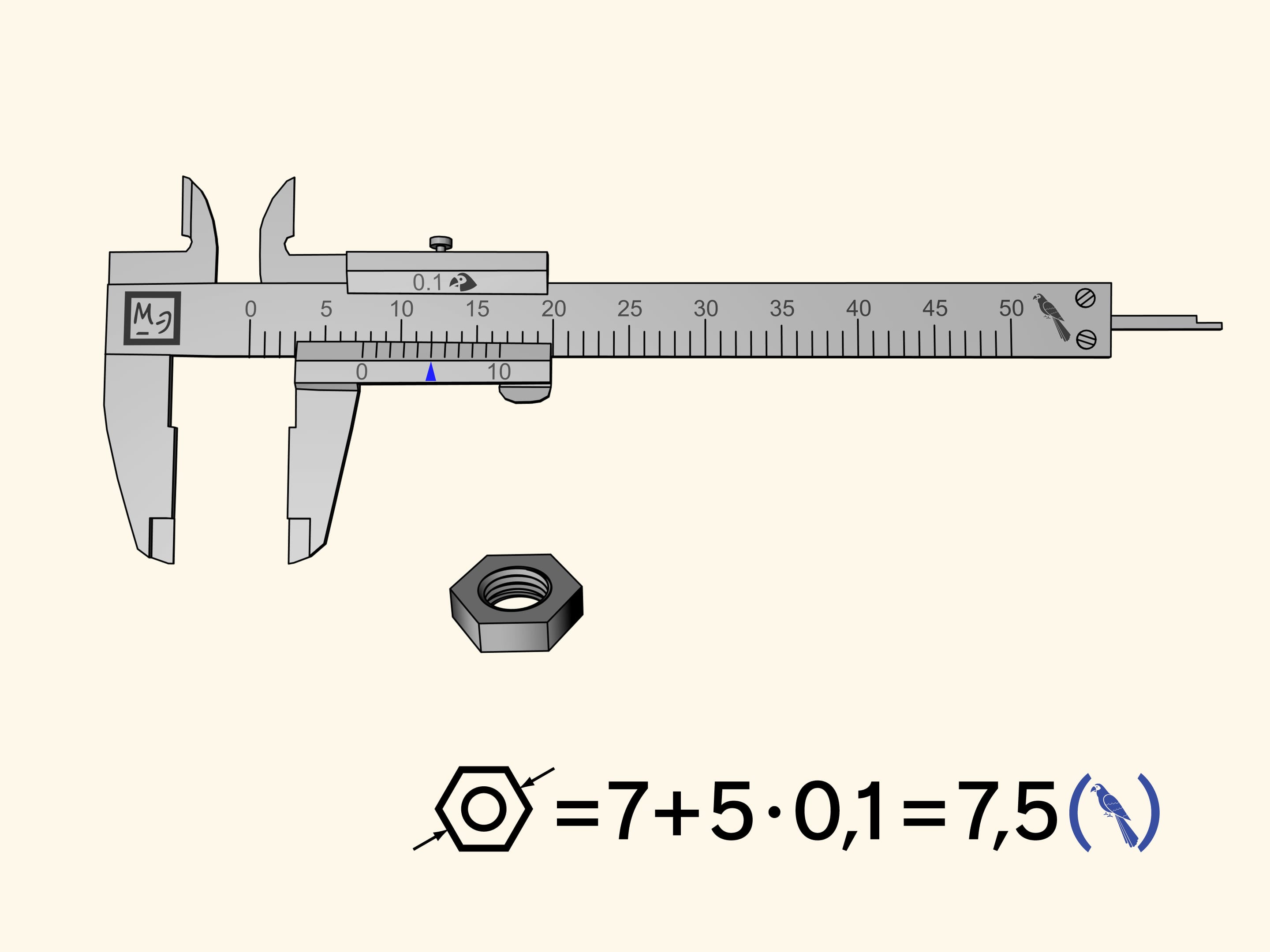
Let us measure the nut again. The zero reference nick will be, as before, between the seventh and the eighth division. This means that our measure contains seven whole parrots. Now observe the divisions of the vernier scale from left to right and look for the nick that coincides with one of the divisions of the main scale. In our case this happens at the fifth nick. Consequently, the measure of the nut is equal to $7 + 5 × 0{.}1 = 7{.}5$ (parrots).
Explain mathematically the argument above. Think how to use the same idea to get measures with more precision.