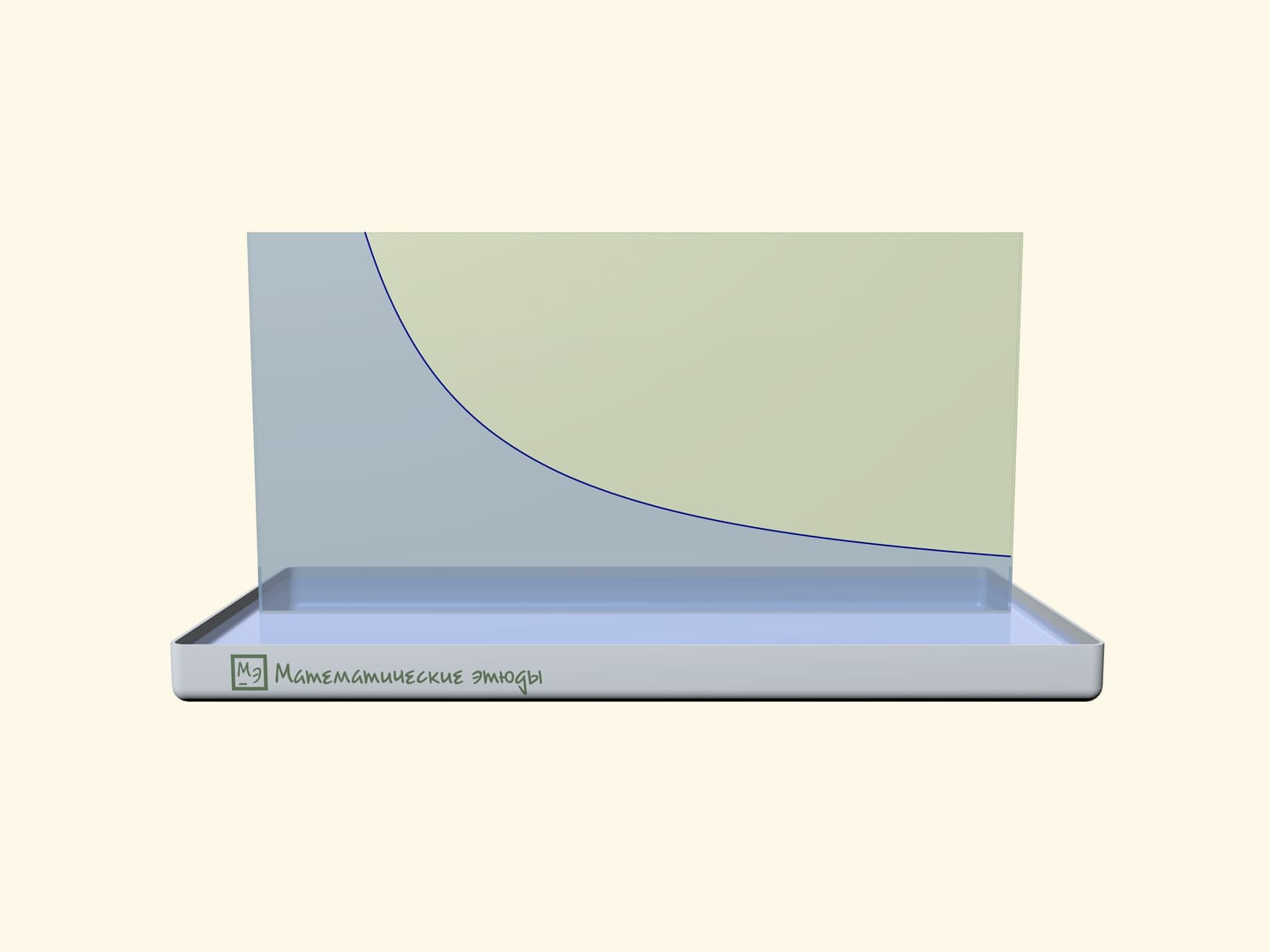
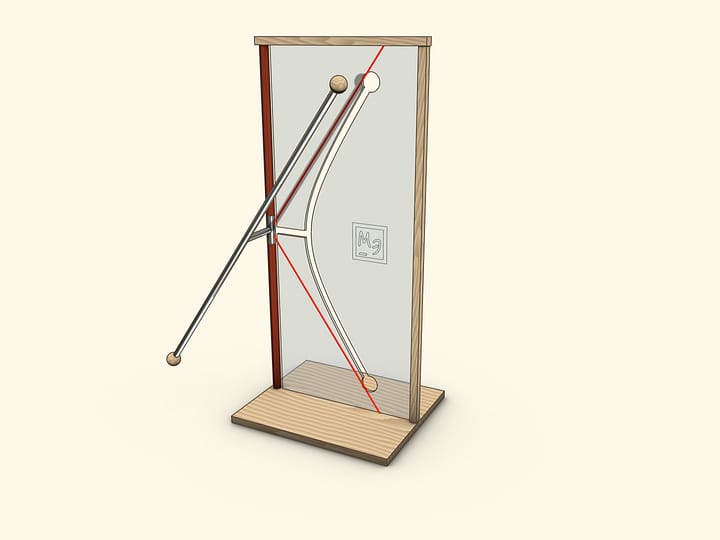
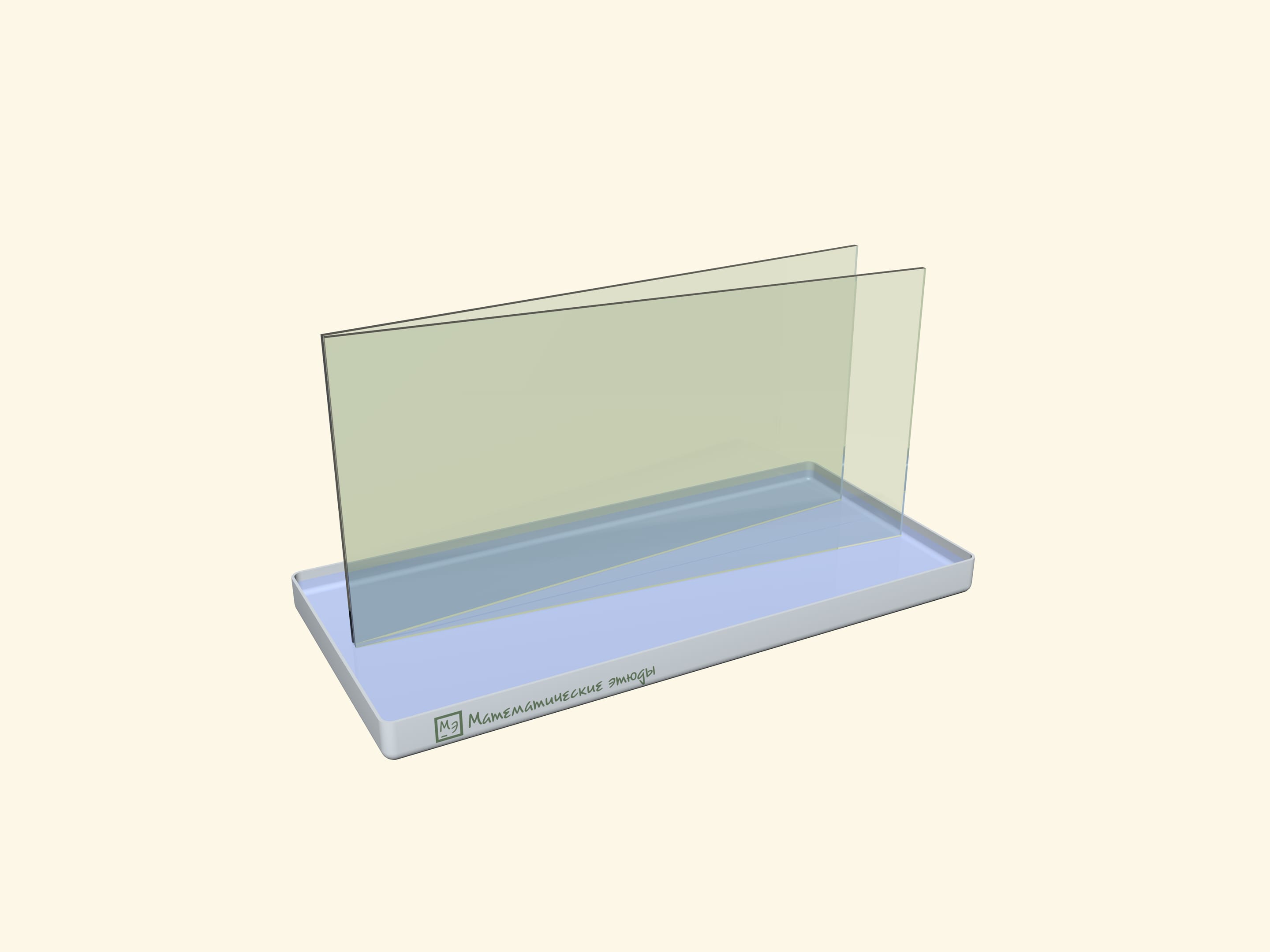
Hyperbola at home can be "drawn" by surface tension forces.
Put two rectangular glass plates in a bath with water. Start to close a “book” slowly: water between plates will rise, and its level will lower according to a familiar curve-hyperbole (which starts with some gap from a “back of a book”).
A reader can receive a physical explanation of the described experiment on his/her own or find it in a magazine “Kvant”.
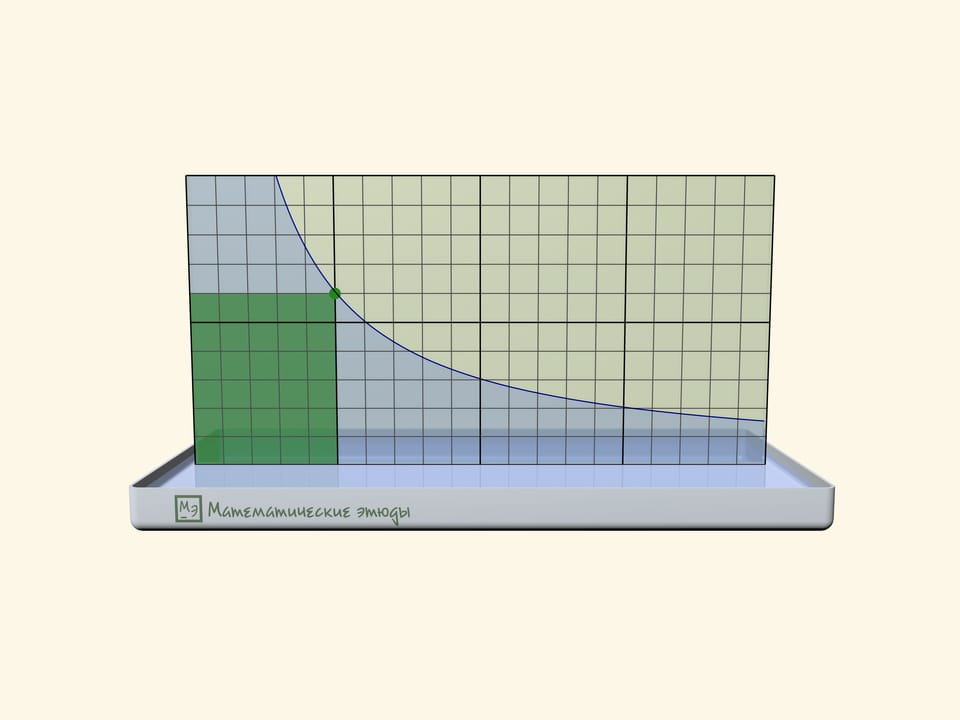
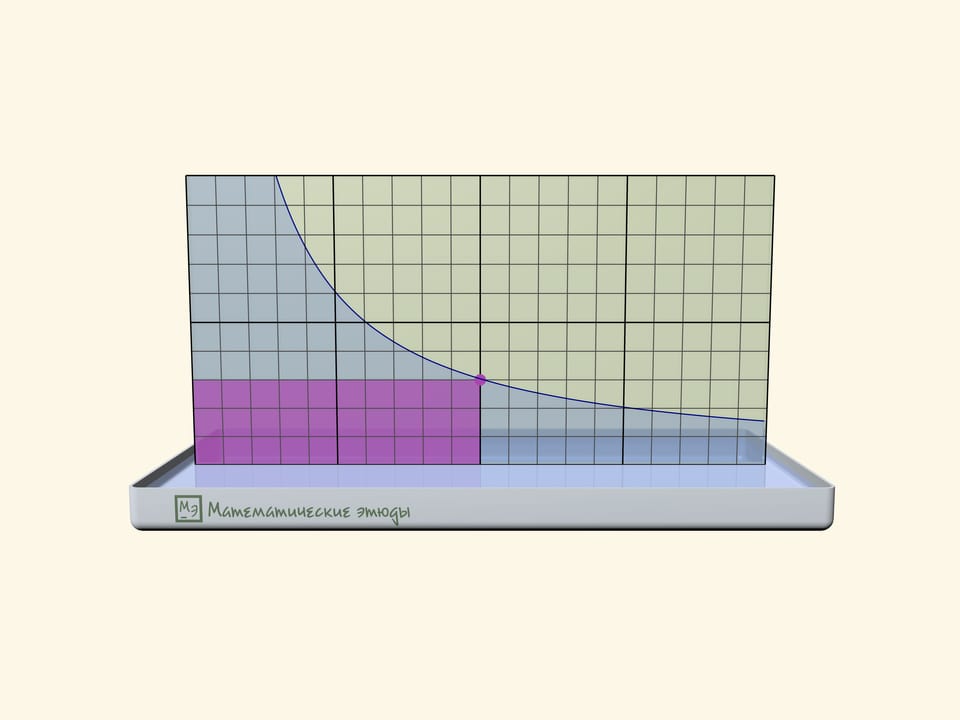
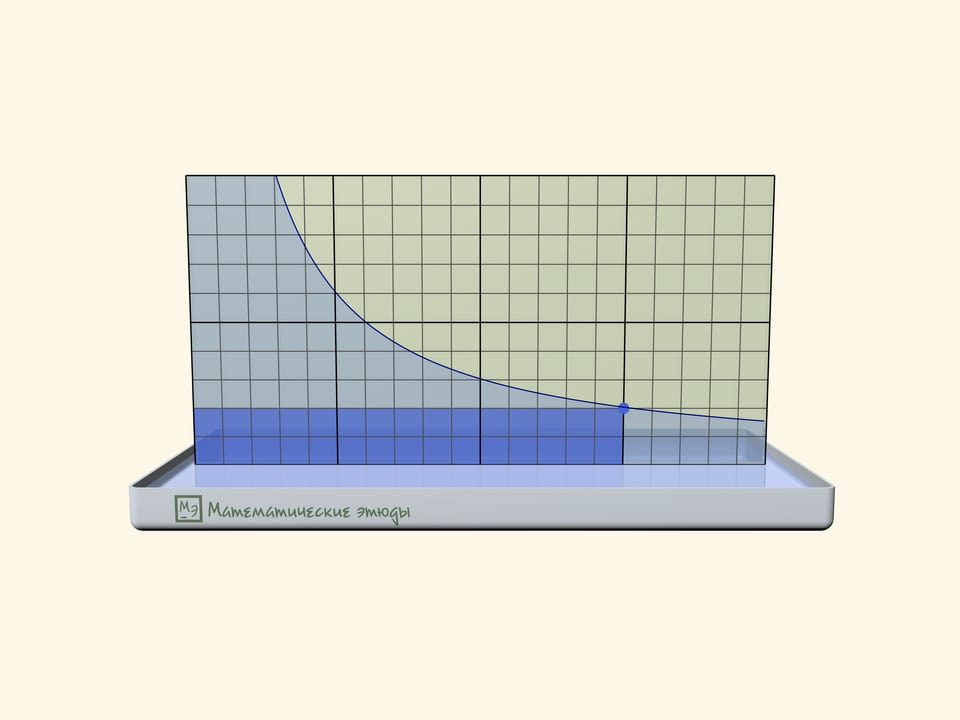
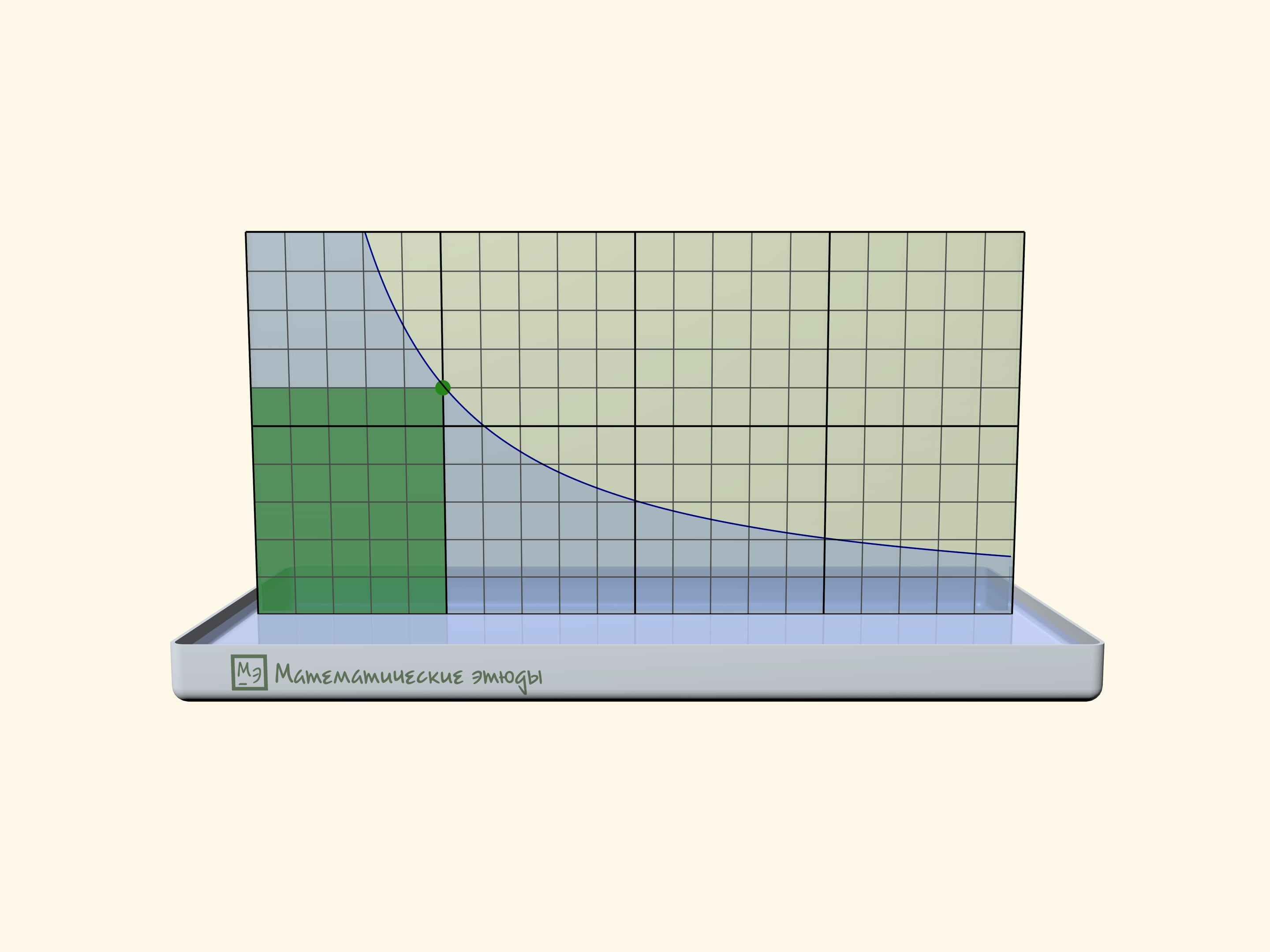
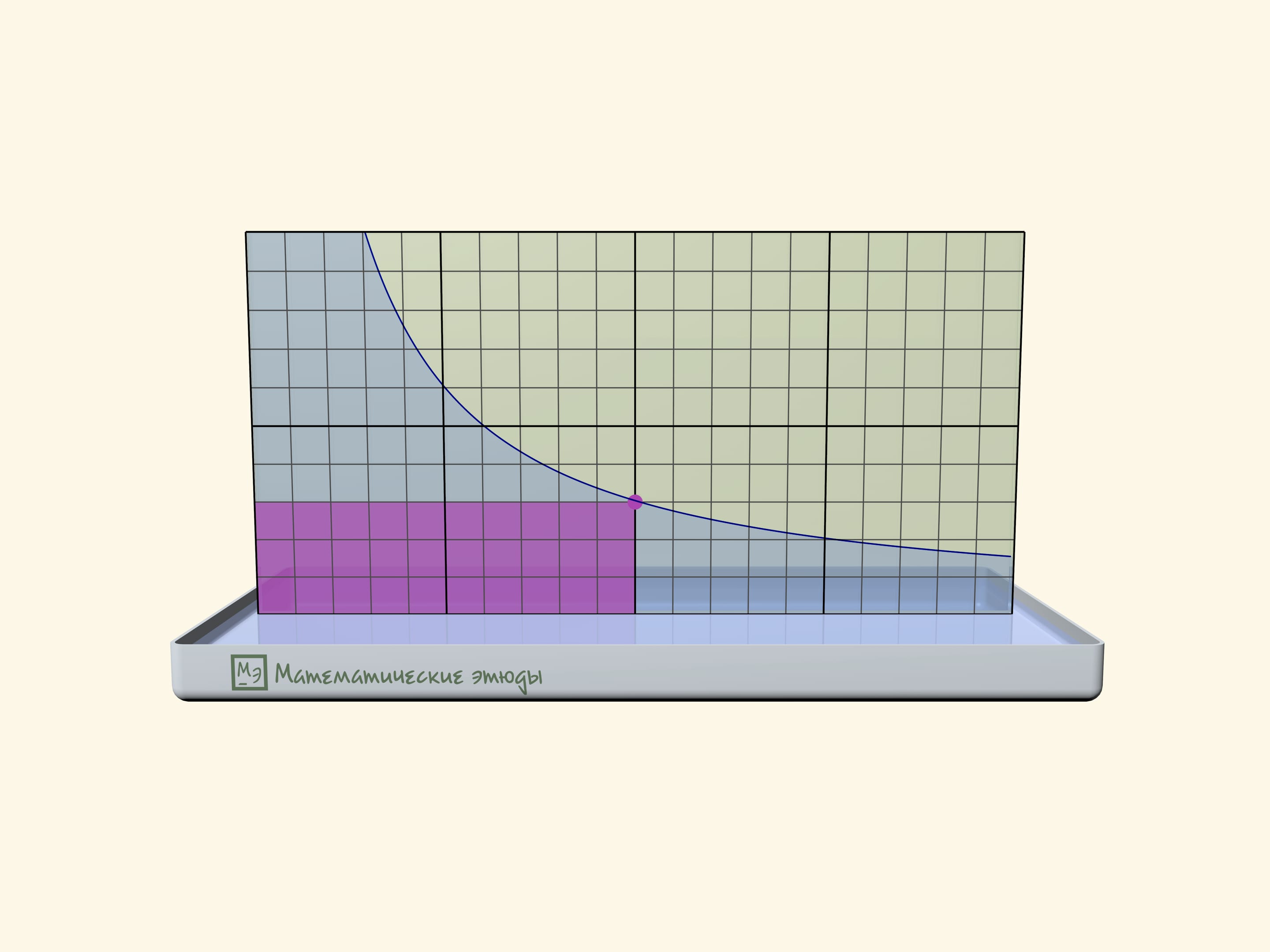
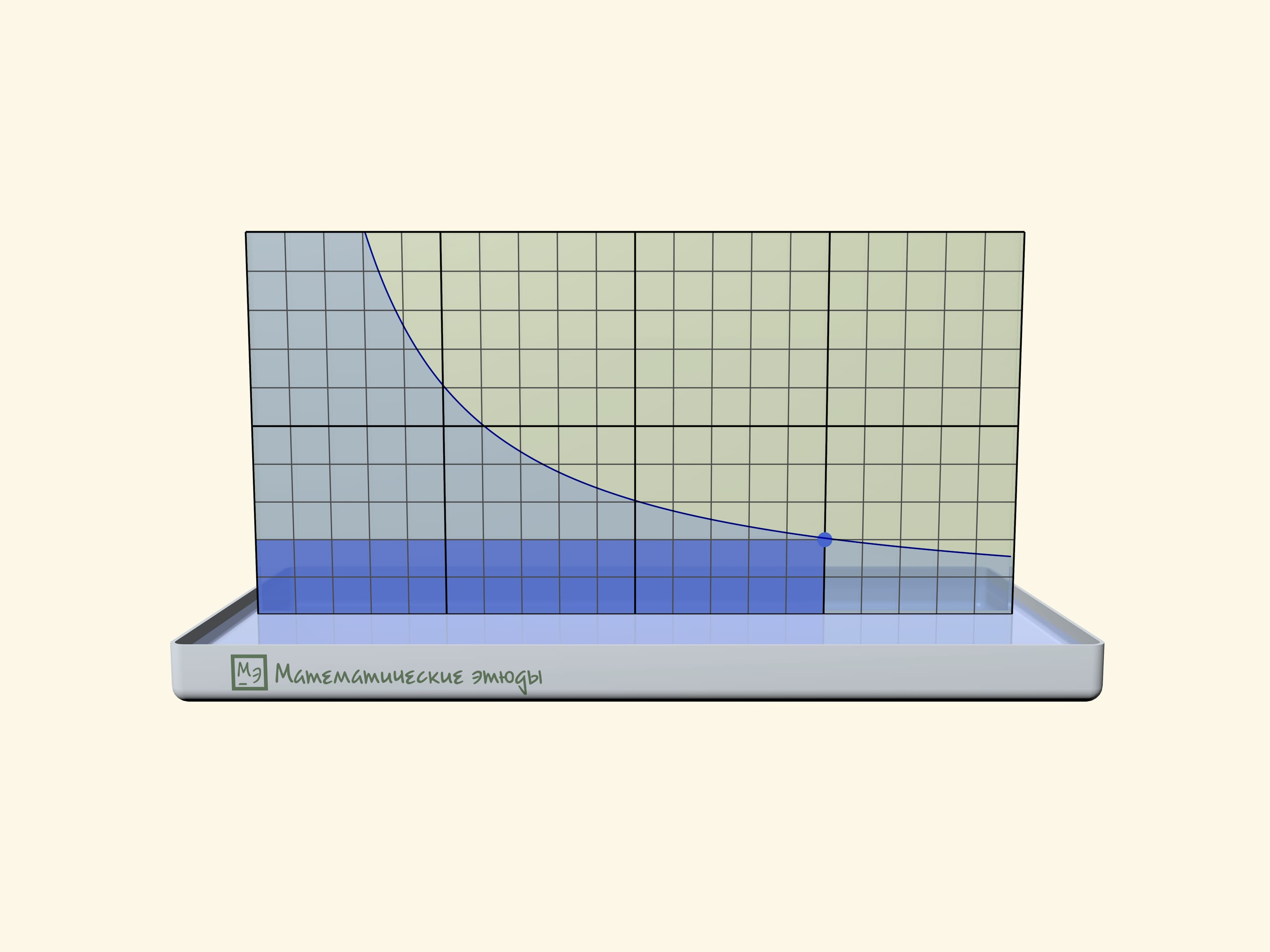
If one previously draws a square net on one glass, one can check that we receive namely a hyperbole: squares of rectangles under the line will be equal.
Rectangles under a hyperbole have become a base of a problem, which has appeared first at Moscow mathematical Olympiad 2020:
Michael marked all points with an abscise $1$, $2$, $3$, … on the function $y=1/x$ graph until he got tired. Then came Maria and coloured all rectangles, where one of peaks is a marked point, one more-the start of coordinates, and two more lie on axes. Then the teacher asked the students to count the square of the figure, which consists of all points, coloured exactly one time. How many points have we received?
The answer that the square is equal exactly to $1$ doesn’t depend on how many points Michael has marked, and can be received both algebraically and geometrically.