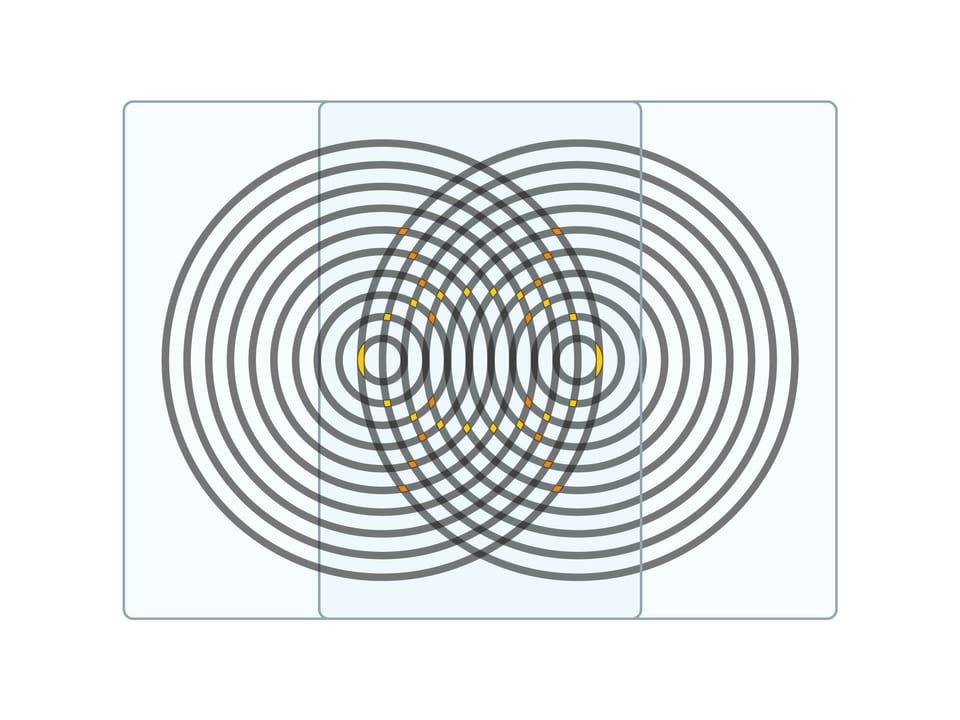
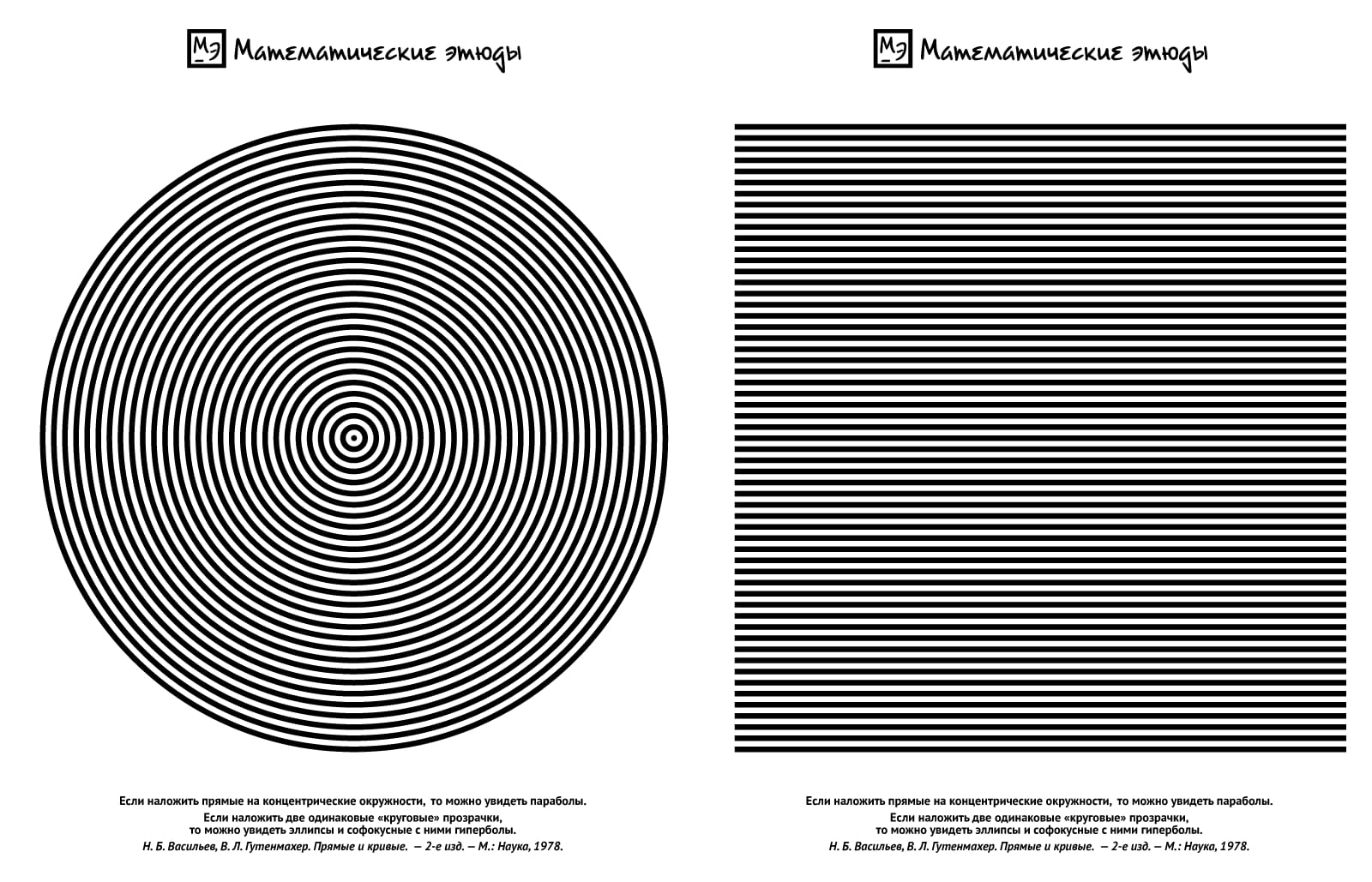
All the conic sections (ellipse, parabola and hyperbola) can be obtained as moiré — an additional geometric pattern that is formed by two overlaying images.
Take a transparency film and print straight stripes at a fixed distance between adjacent ones. On another film, print circular stripes (concentric circles) of the same width and with the same distance between adjacent ones.
If we overlay concentric circles with straight lines, one can see a family of parabolas. Every parabola is a chain of opposite vertices of curvilinear quadrilaterals, bounded by adjacent lines and adjacent circles. Shifting the sheets, one can see parameters of the parabola family changing and ponder the position of the directrix and the focus on the basis of the parabola definition.
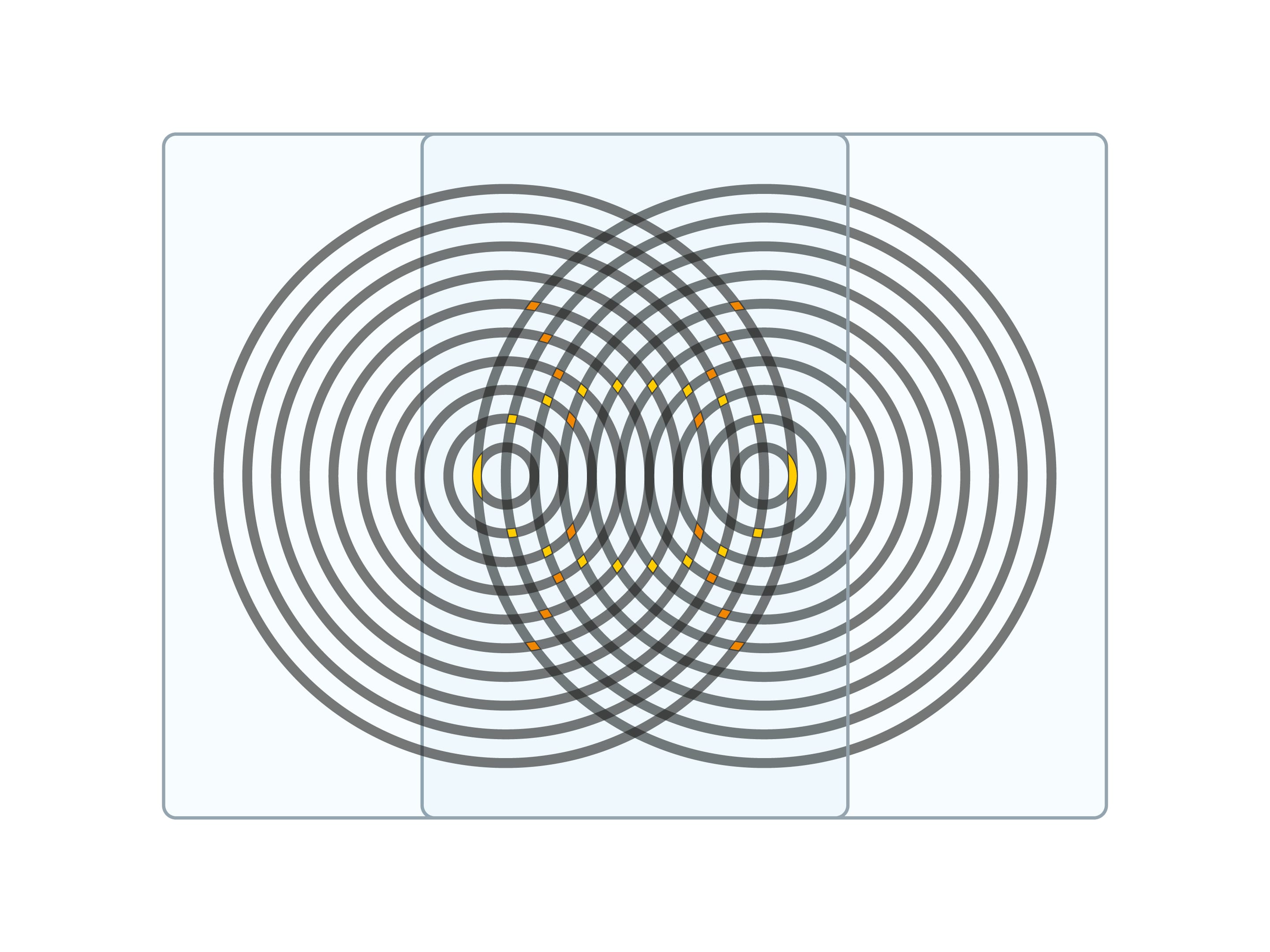
If one overlays two identical “сircular” sheets, one can see ellipses and intersecting them hyperbolas with common focuses which are the centres of circles. And in this case, too, shifting the sheets helps to spot these curves and track the curves’ parameters change.