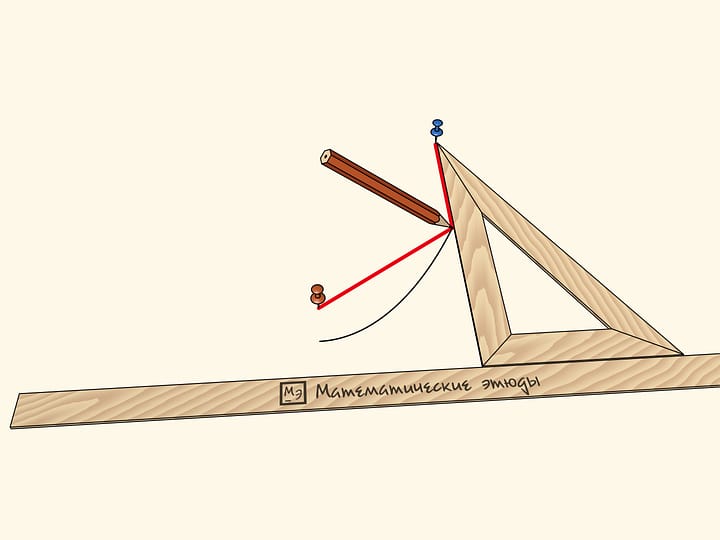
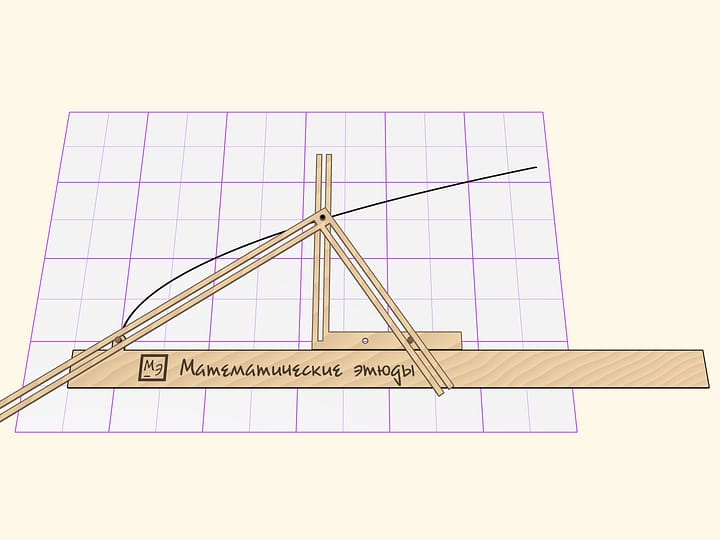
According to the optical property of parabolas, a ray falling parallel to parabola’s axis gets to its focus after reflecting from its surface. A parabolic billiard model demonstrates the optical property using mechanics.
One of the billiard’s sides has a form of parabola. The pocket is in its focus. A slide fixed on the guide rail can be moved, but at any position it remains parallel to parabola’s axis. A ball rolling down the slide always makes it to the pocket!
When manufacturing, it is worth picking the parabola’s parameters so that the pocket (parabola’s focus) was nor too close neither too far from the vertex.
The slide should rest against the straight side of the billiard to stay parallel to its axis when shifted.
The ball, the slide height and the billiard’s surface material should be chosen so that after reflecting from the wall the ball would not reach the pocket too fast — flying over the pocket rather than falling in it.
Other models in “Conic sections: parabola”
