Regular polyhedra are naturally related to each other. This is both the duality of regular polyhedra and all possible ways to inscribe one polyhedron into another. Yet the apparent encounter with this interrelation is sometimes surprising.
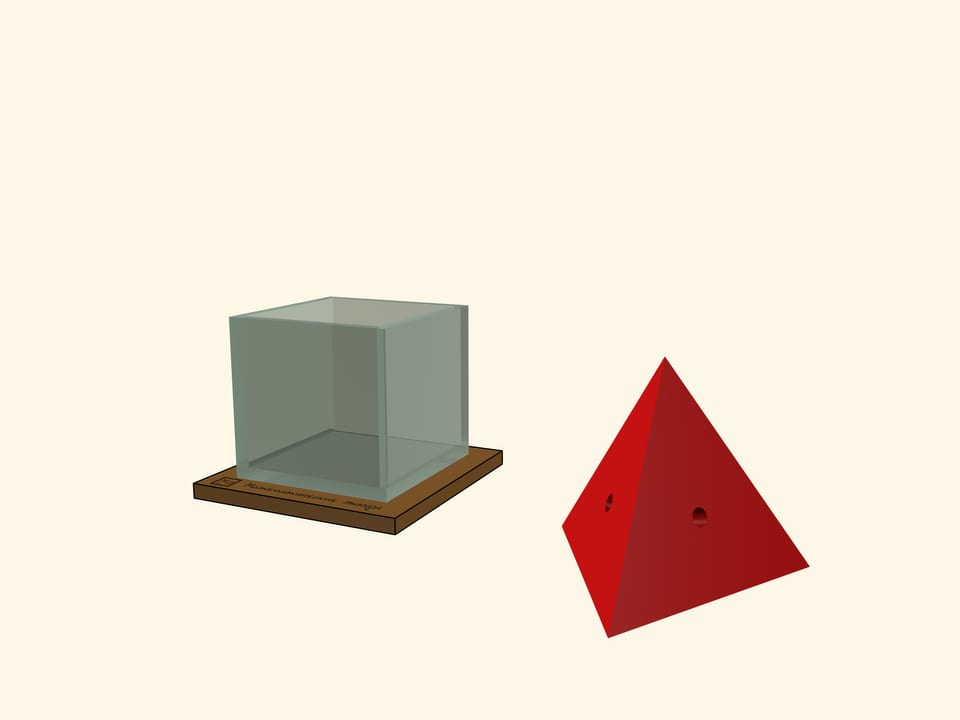
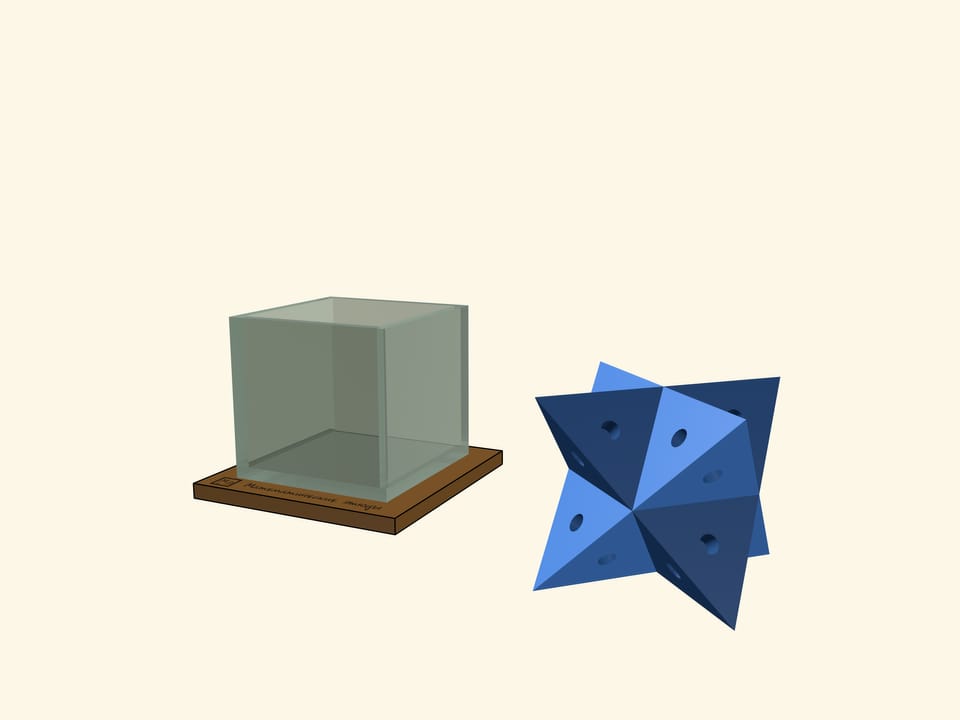
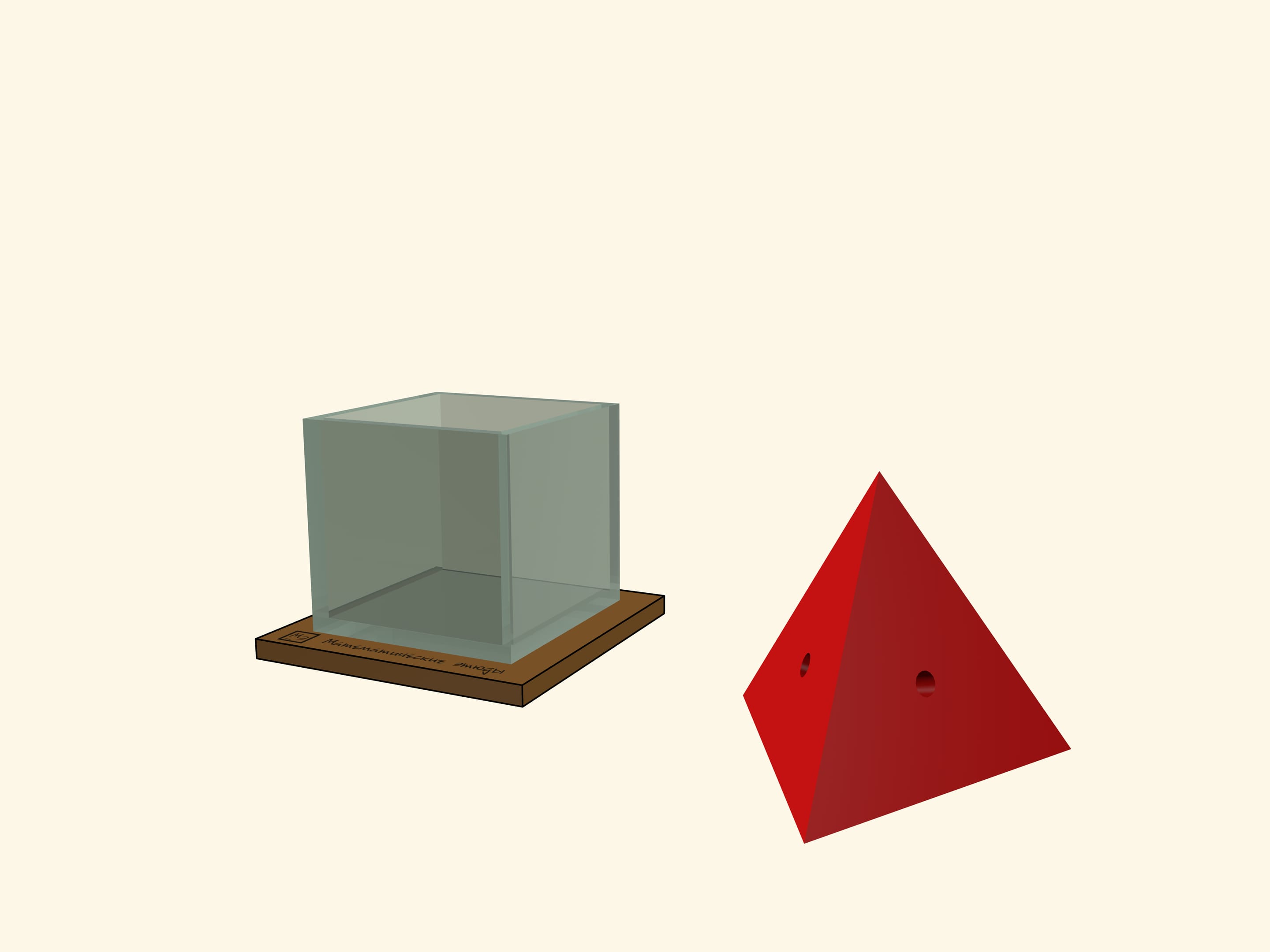
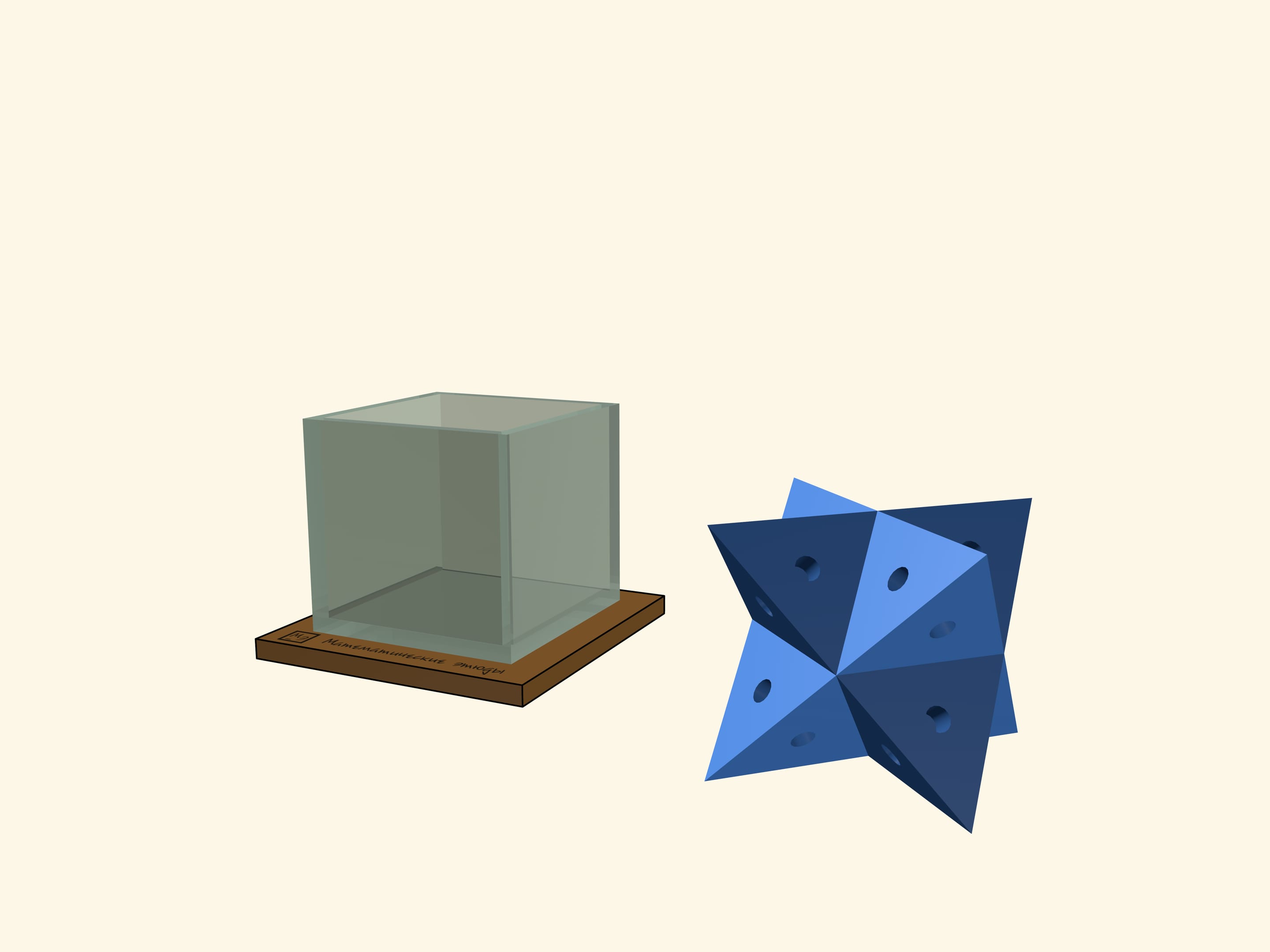
The basis of the model, which amazes both children and adults, is a cube without a top edge, made of glass or acrylic. The set includes several polyhedra, which are better cut from a lightweight material, such as foam. If the size of the cube is large, the polyhedra should have holes for fingers.
The most amazing polyhedron which can be put into a cube is a "large" tetrahedron. At first glance there is no way it could fit inside, but that is if we do not know that a tetrahedron can be inscribed into a cube so that all the vertices of the tetrahedron coincide with the vertices of the cube. As a variation one can take two "opposite" tetrahedrons. Such a polyhedron — the union of these tetrahedrons — was considered by Johannes Kepler, and he named it "stella octangula".
The crossing of the cube and its dual octahedron, enlarged so that their edges intersect, is a cubo-octahedron. This semiregular polyhedron appears in both the Star Trek movies and the Elite video game. Being obtained as a truncation of a cube, it can be placed inside the cube.
It is interesting and useful to see "live" the way another regular polyhedron, the icosahedron, fits into the cube: an icosahedron edge will lie "in the centre" of each face of the cube.
And how many children can fit into a cubic metre? If you conduct an experiment by making a safe cube with an edge of one meter and no top edge, children will have fun and you will be surprised with the result!