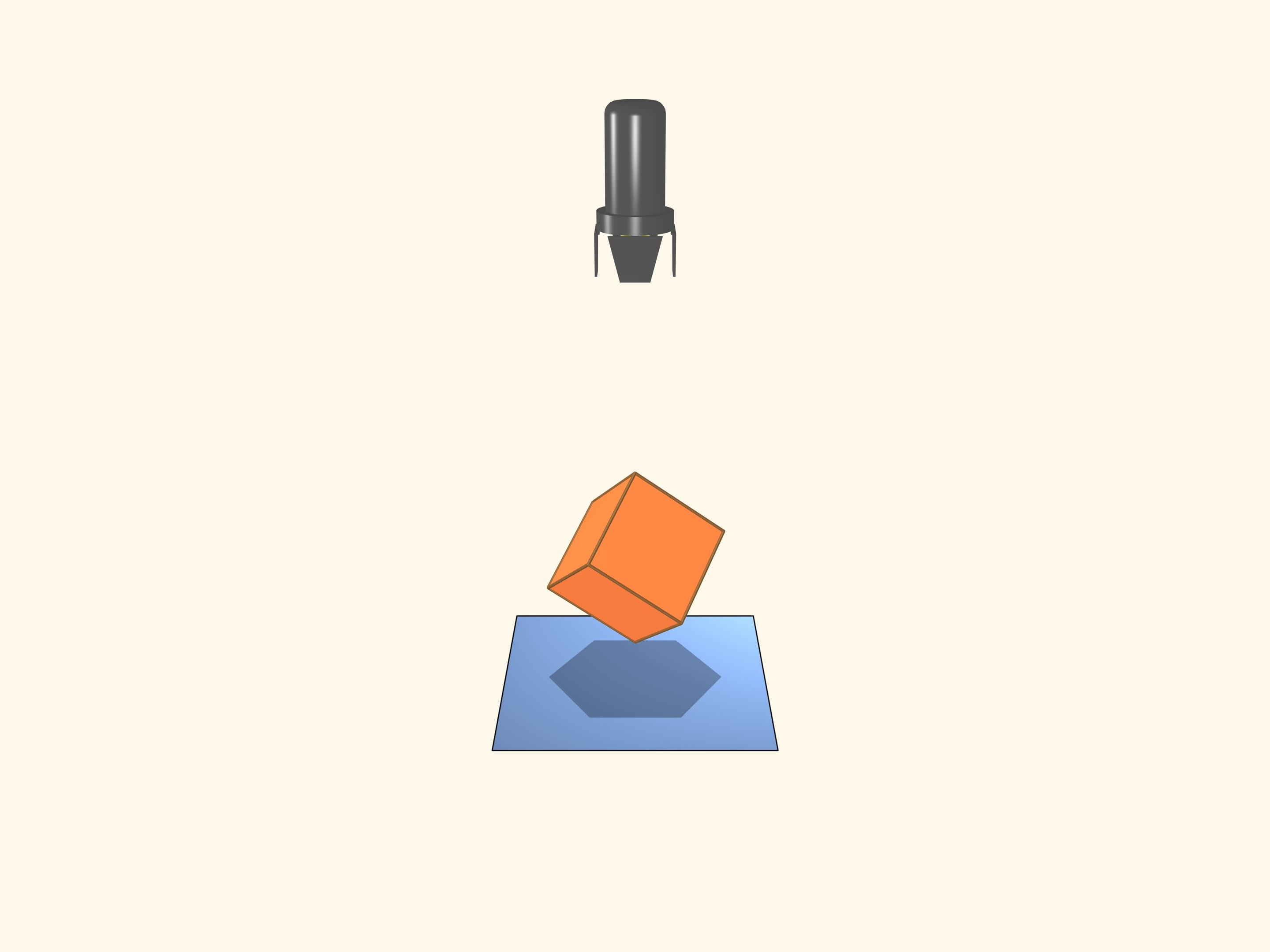
Take a projector generating parallel rays. It's obvious that a cube may have a square shadow. But what is the maximum number of vertices that may have the polygon forming the shadow of a cube? If the diagonal of the cube is parallel to the rays, the shadow will be a regular hexagon!
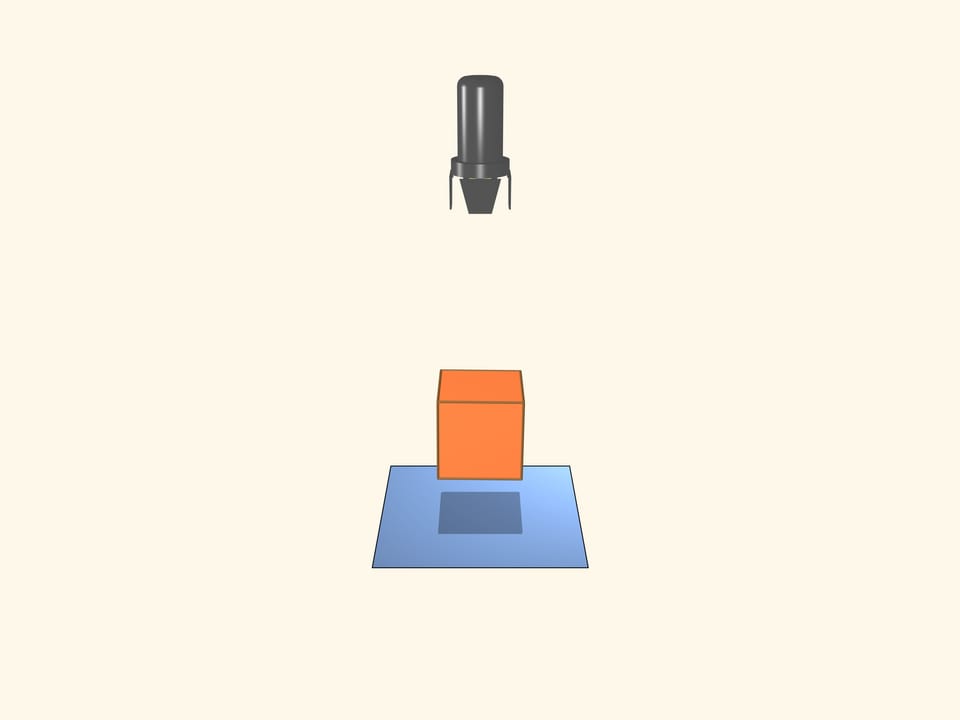
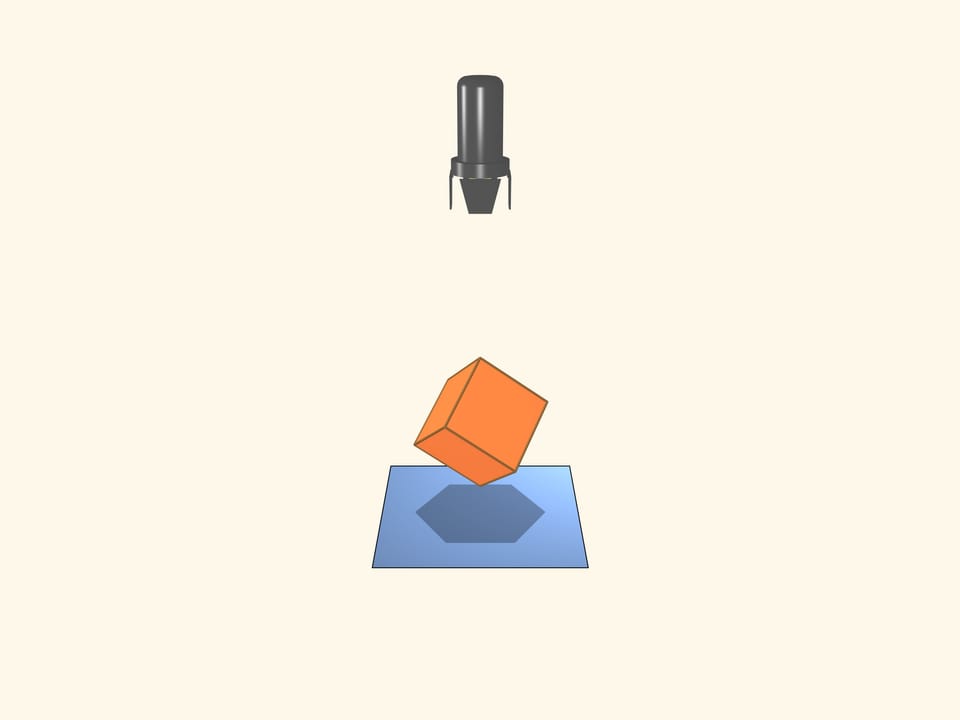
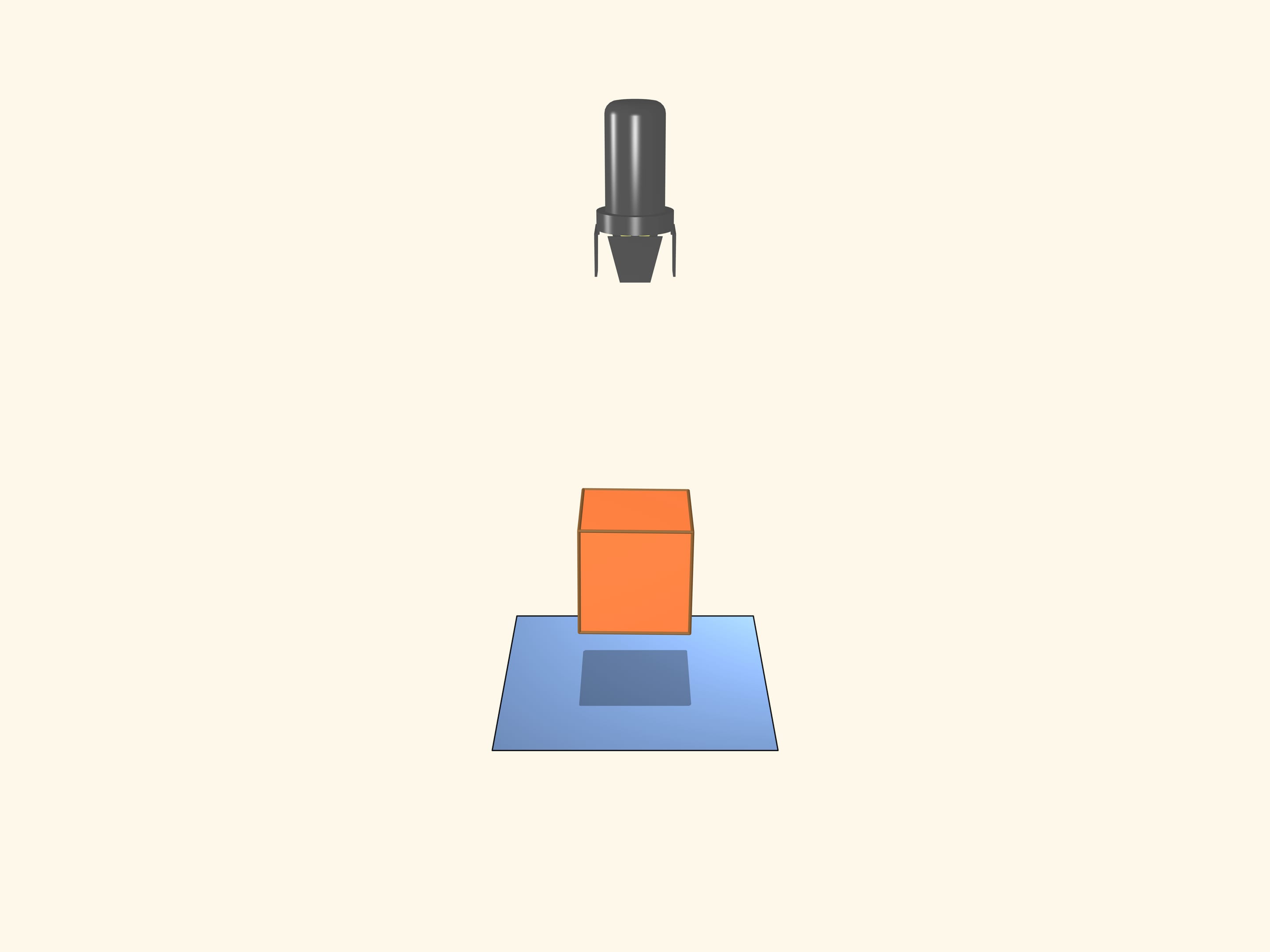
Let's turn both the projector and the screen. The shadow on the screen is a square. Does our object have to be a cube?
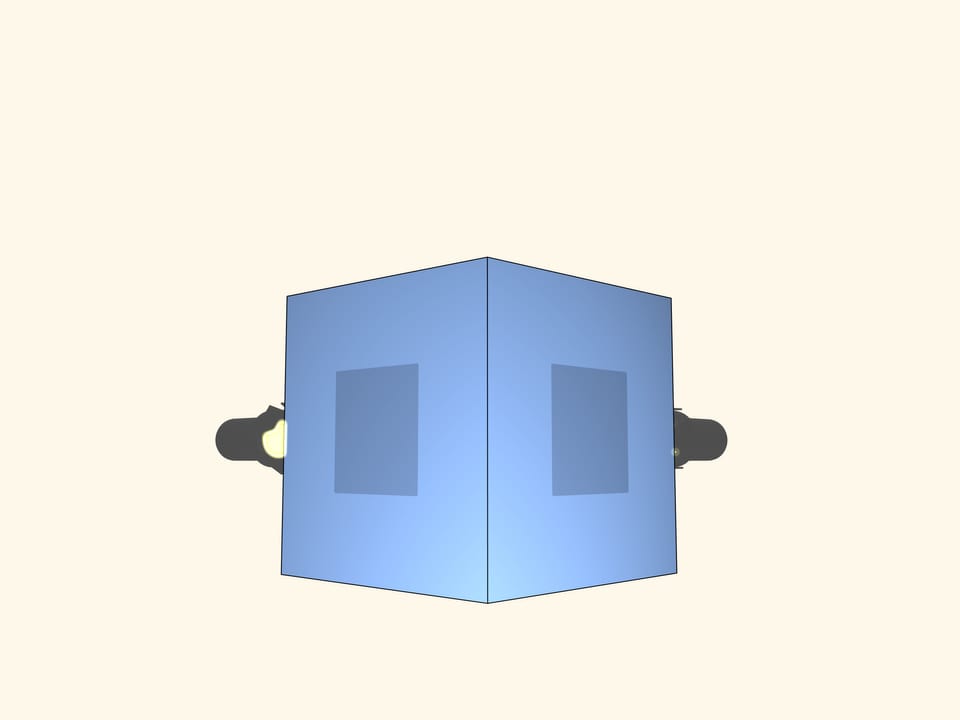
Add another screen and projector in direction perpendicular to the first one. Now we have two orthogonal projections forming squares. Is it definitely a cube now?
And what if three orthogonal projections? are squares? Is there a body except for cubes forming three orthogonal square shadows?
It's easy to imagine non-convex bodies, e.g. a cube with holes, giving such projections. And what if we consider only convex bodies, or even regular polytopes?
It turns out that even a regular polytope different from a cube may form square shadows in three orthogonal directions.
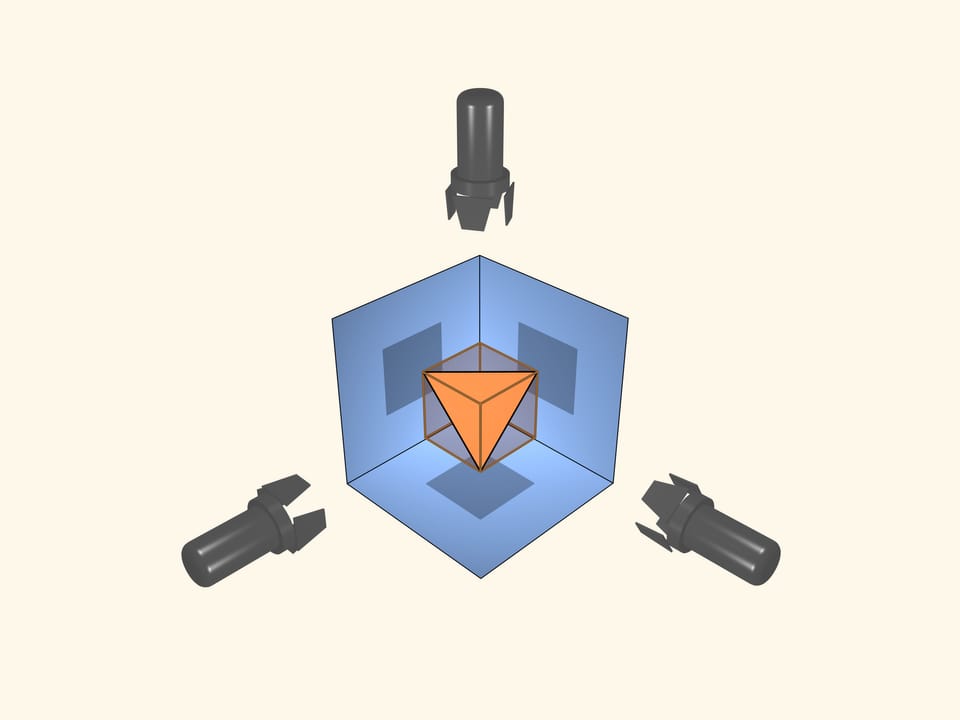
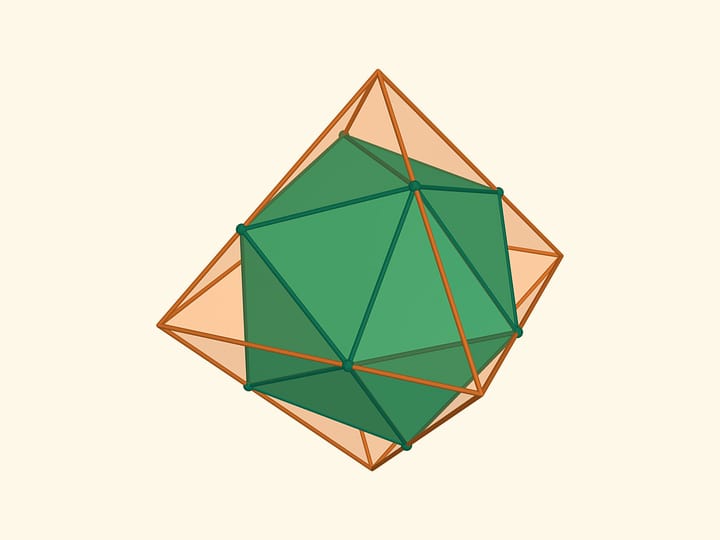
Indeed, we can inscribe a regular tetrahedron in a cube! Four vertices of the tetrahedron will coincide with the vertices of the cube. All the edges of the tetrahedron will be diagonals of the cube's faces, and as follows, equal.
If we look through one of the cube's faces, such a tetrahedron will «fill» the whole projection along the direction perpendicular to the face.
It means that if a cube is placed so that it's three orthogonal projections are squares, i.e. the screens are parallel to the faces, the inscribed tetrahedron will give the same shadows, three squares.