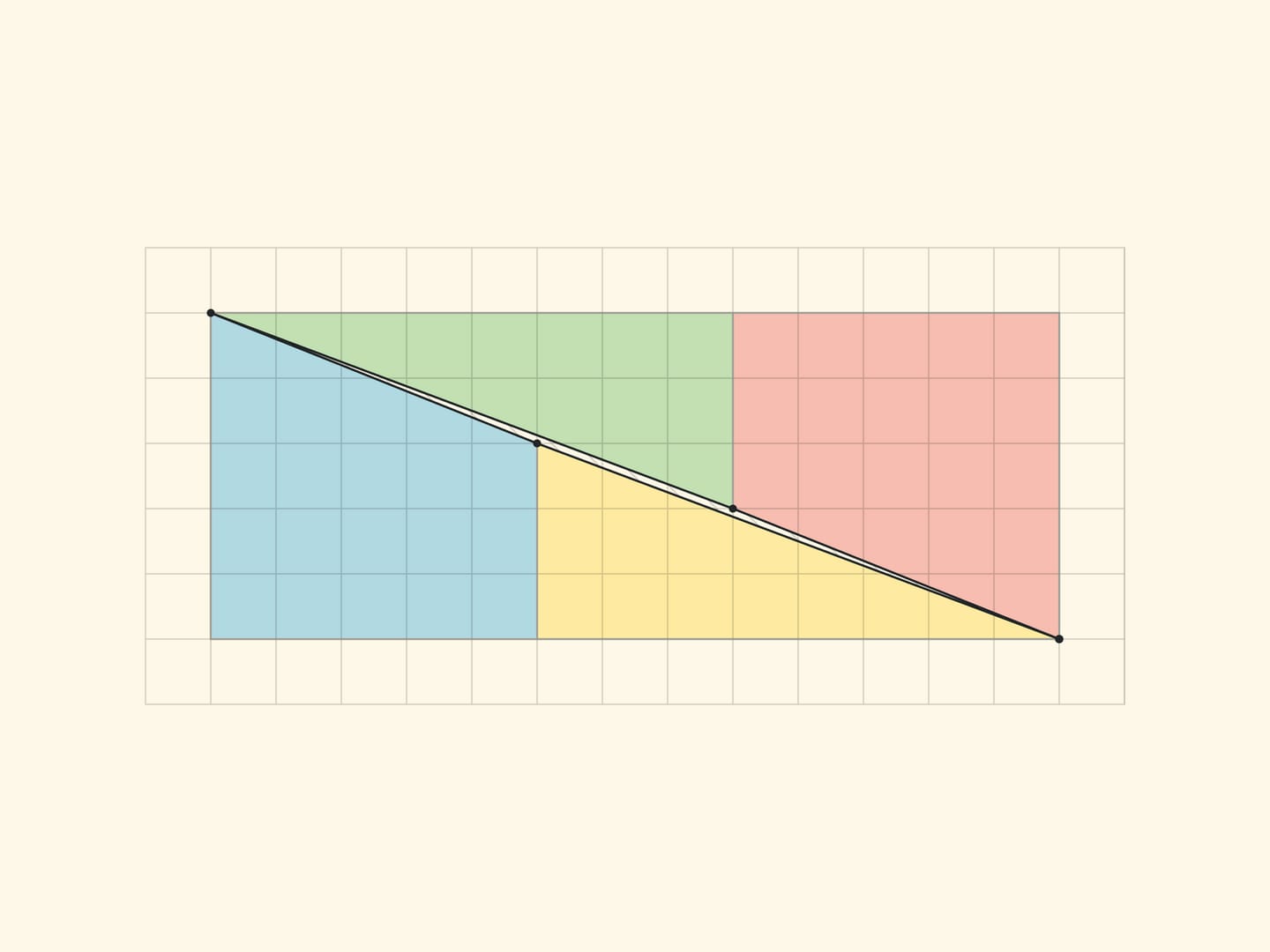
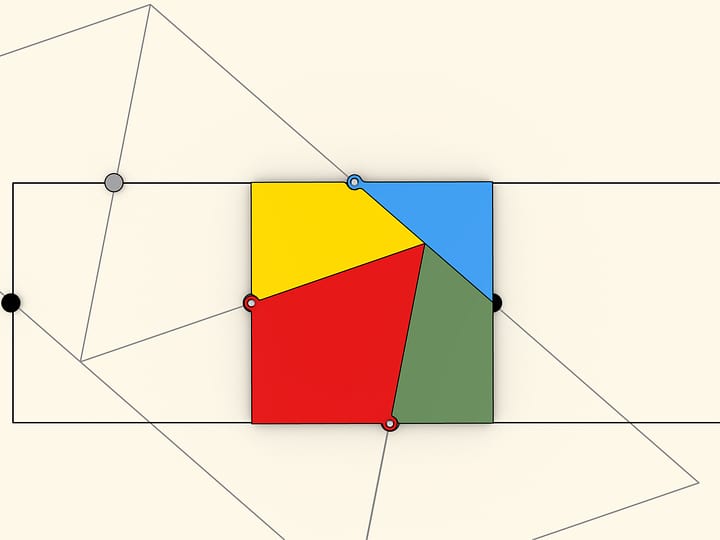
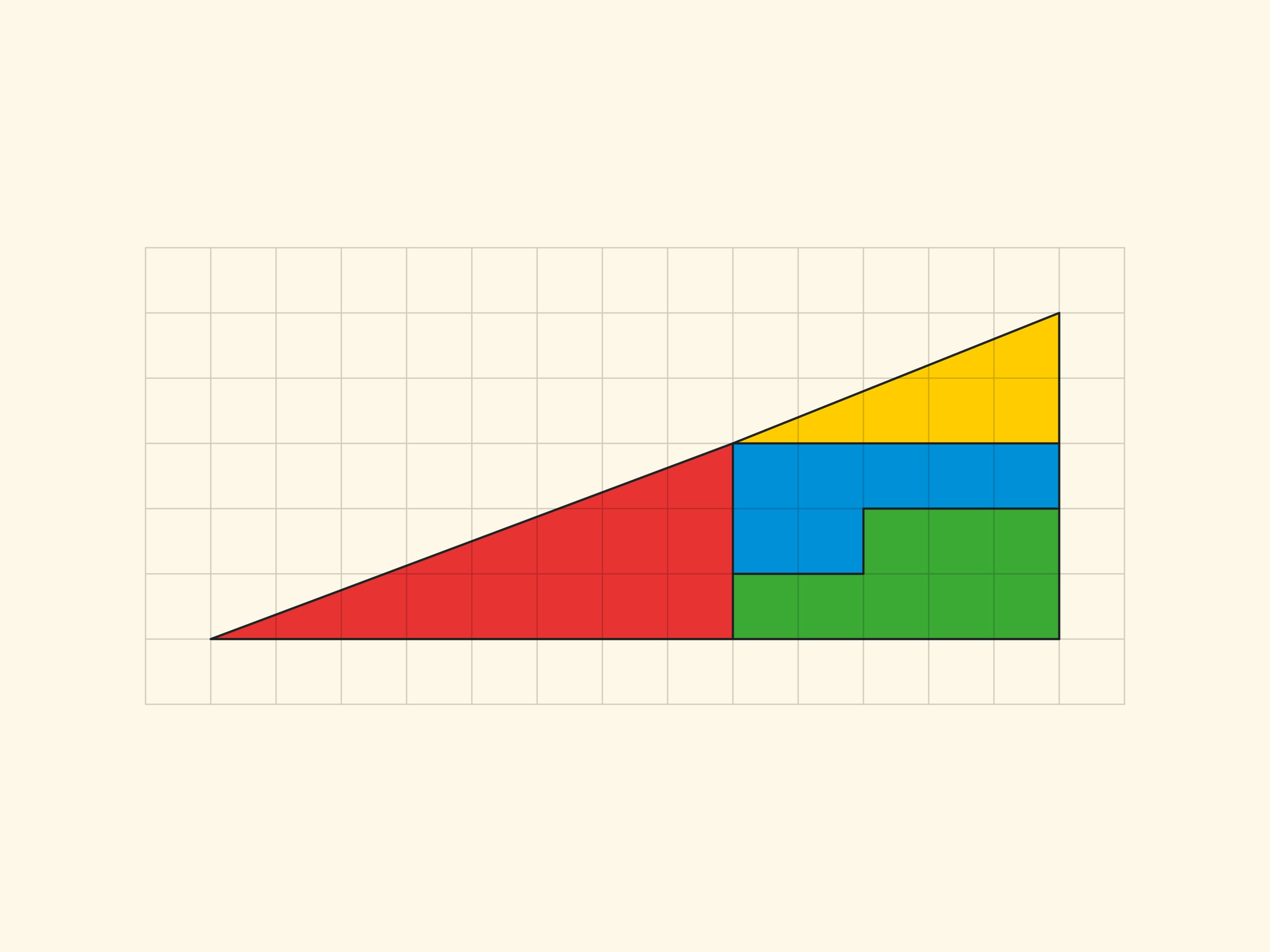
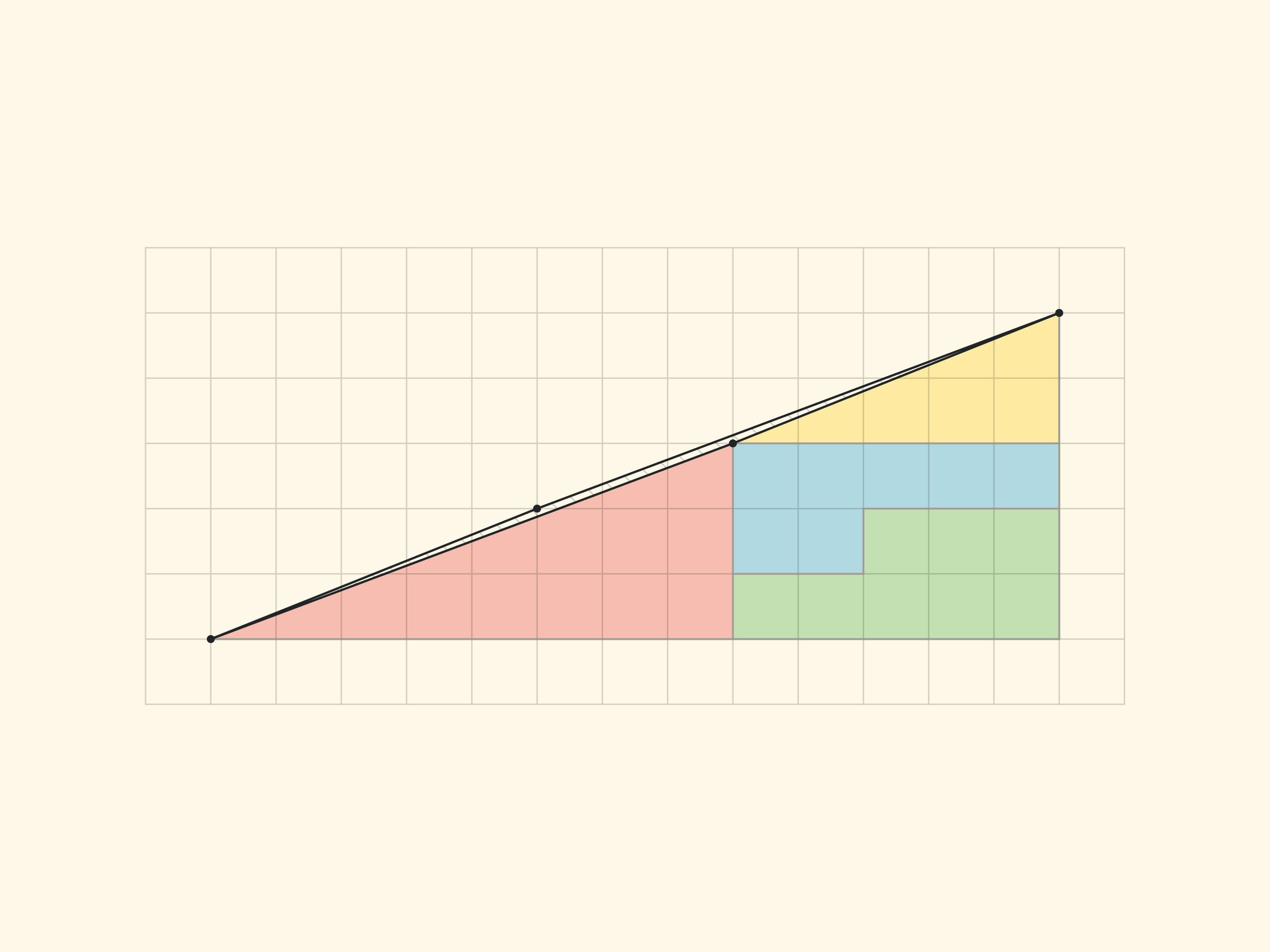
A square $8\times 8$ can be cut into four parts from which a rectangle $5\times 13$ of area $65$ is formed!
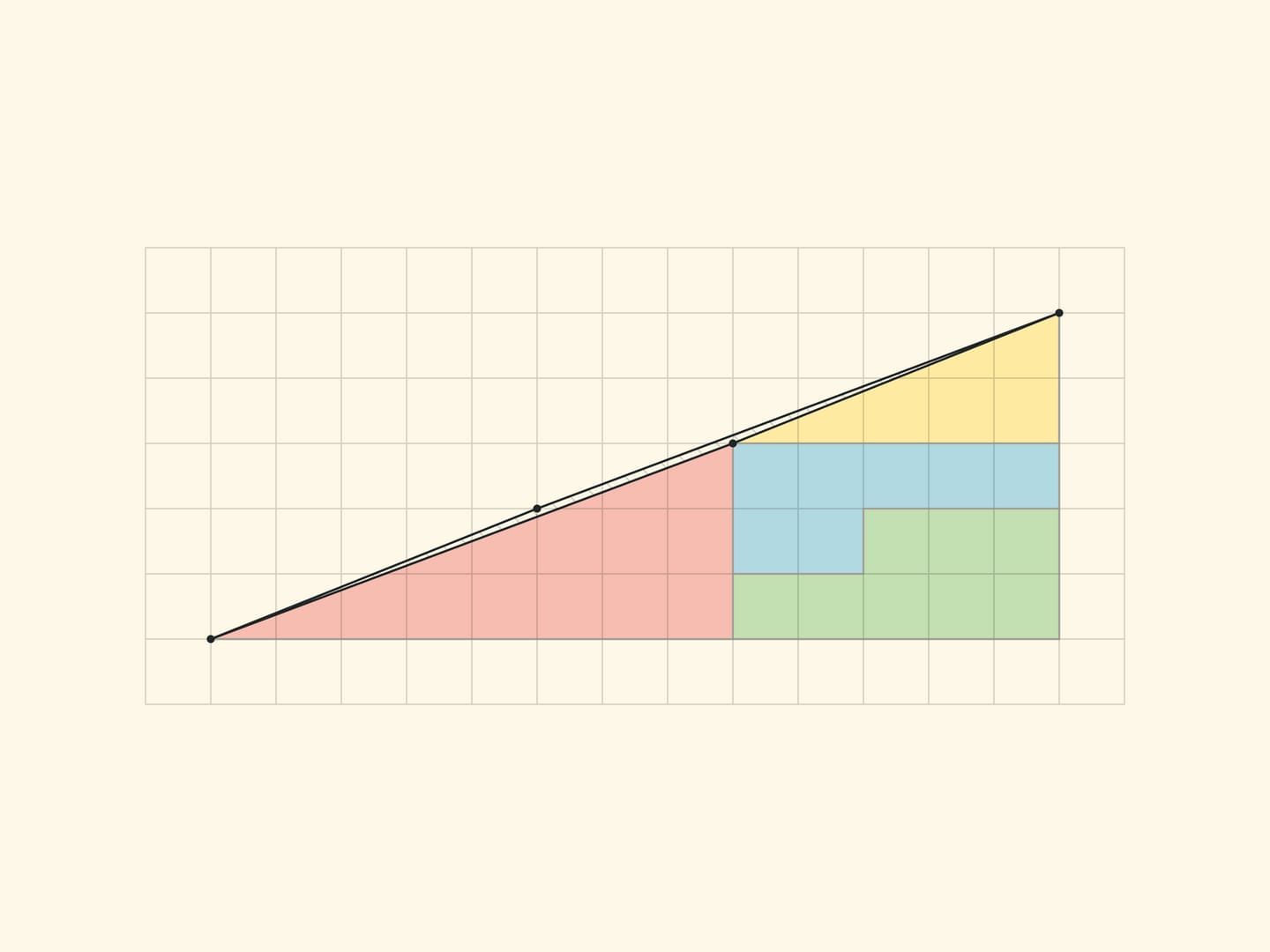
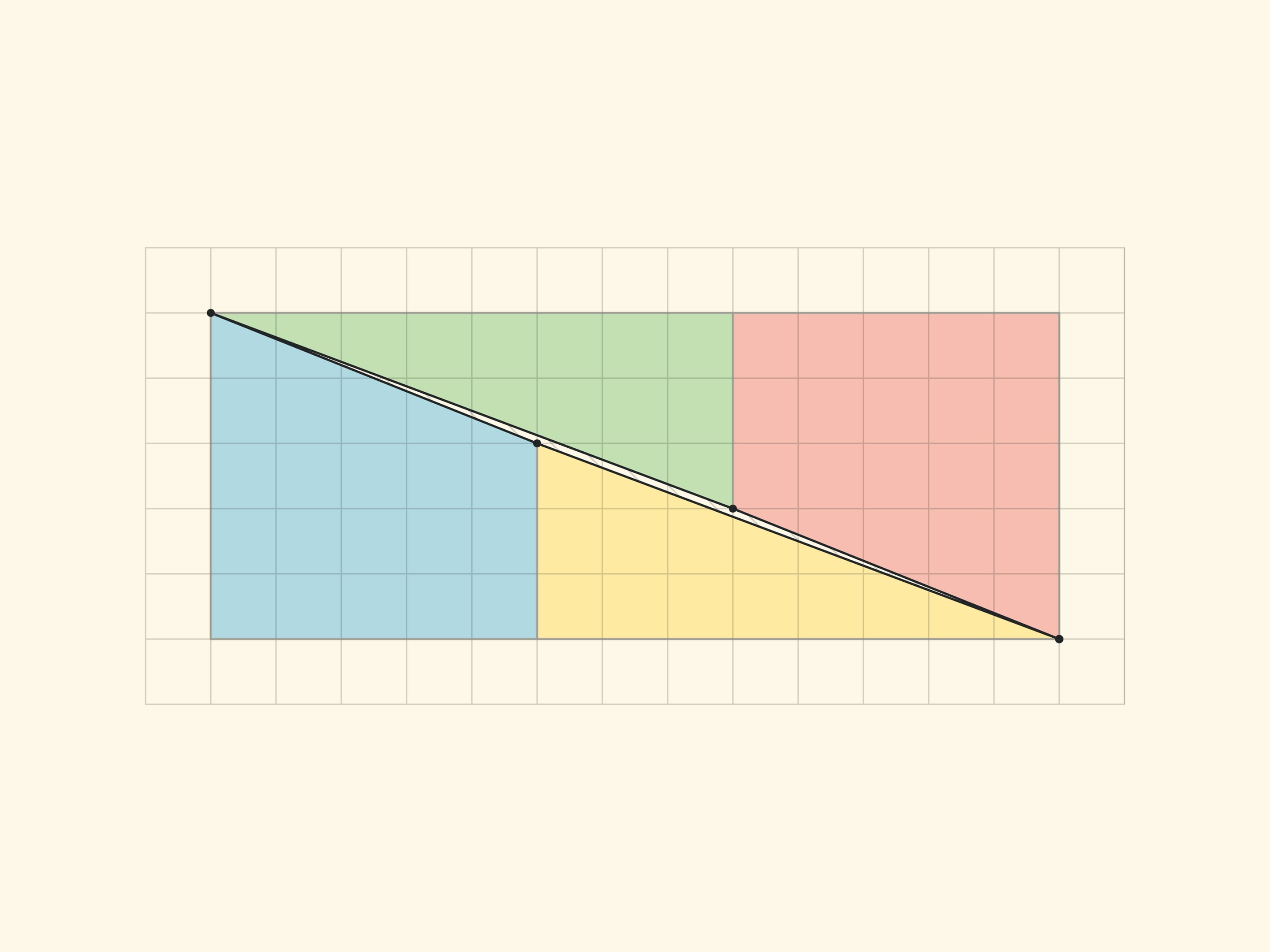
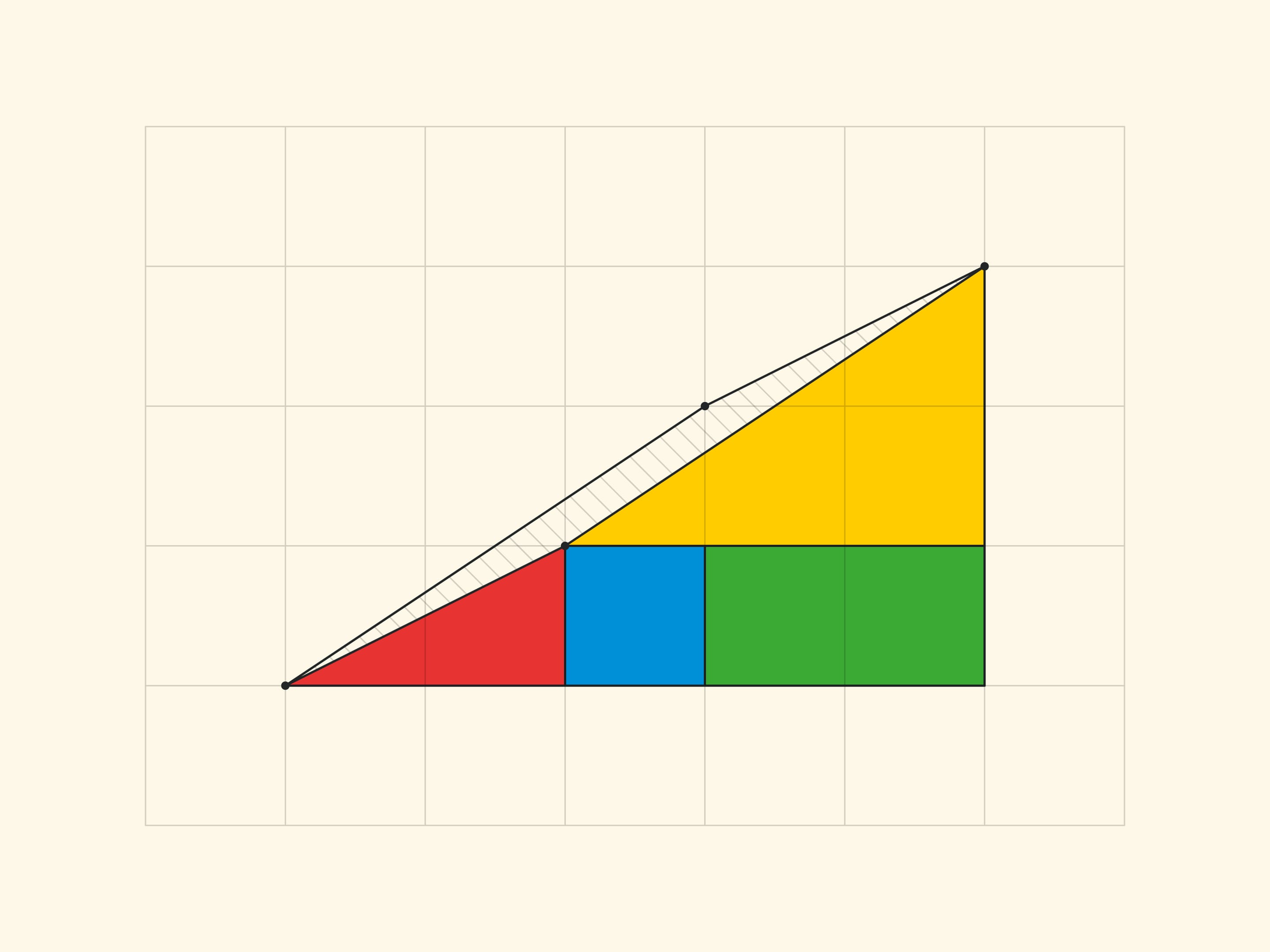
Another well-known geometric sophism: a right triangle with cathetuses of $5$ and $13$ is being cut into four parts, which make up the same right triangle, but with one empty cell!
But wait, the area of the figure is equal to the sum of the areas of the parts of which it is made up. So it can’t change when you rearrange it. What is the discrepancy?
The explanation of the paradox in both cases is essentially the same — the pieces being considered are not the ones described. In the “Chessboard Paradox”, presented by chess player and puzzle author Samuel Loyd in the mid XIX century at the Chess Congress, the square is transposed not into a rectangle, but into a rectangle without an elongated, almost imperceptible to the eye, parallelogram of a unit area (stretched along the diagonal of the rectangle). In the triangle paradox, invented by Martin Gardner in the middle of the XX century, both hypotenuses (of the original triangle and the resulting triangle) are not actually straight lines: the figure made up of them is also a parallelogram of unit area.
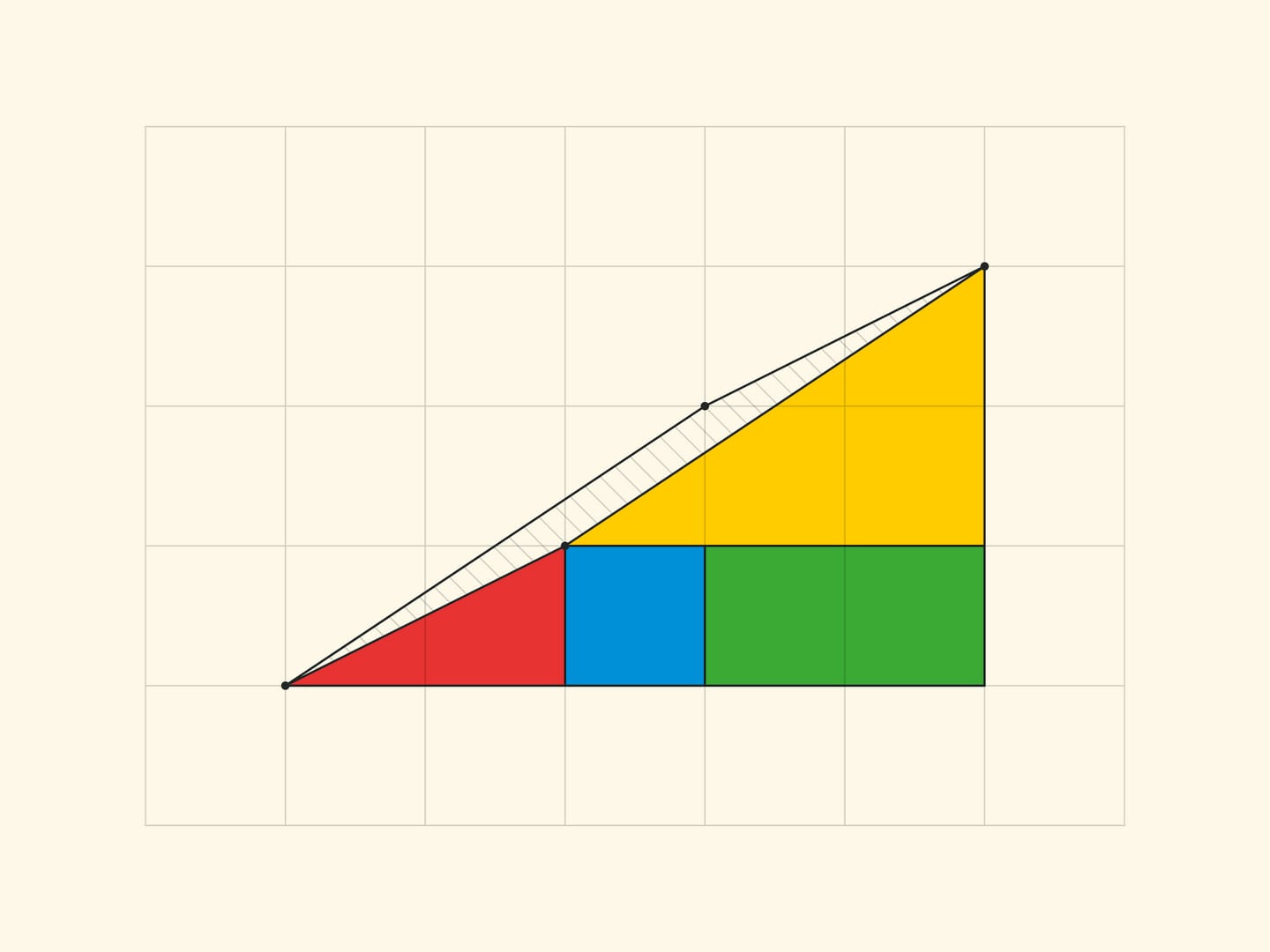
To make it easier to see this parallelogram, let us look at an analogue of a smaller Gardner triangle — with sides of $3$ and $5$.
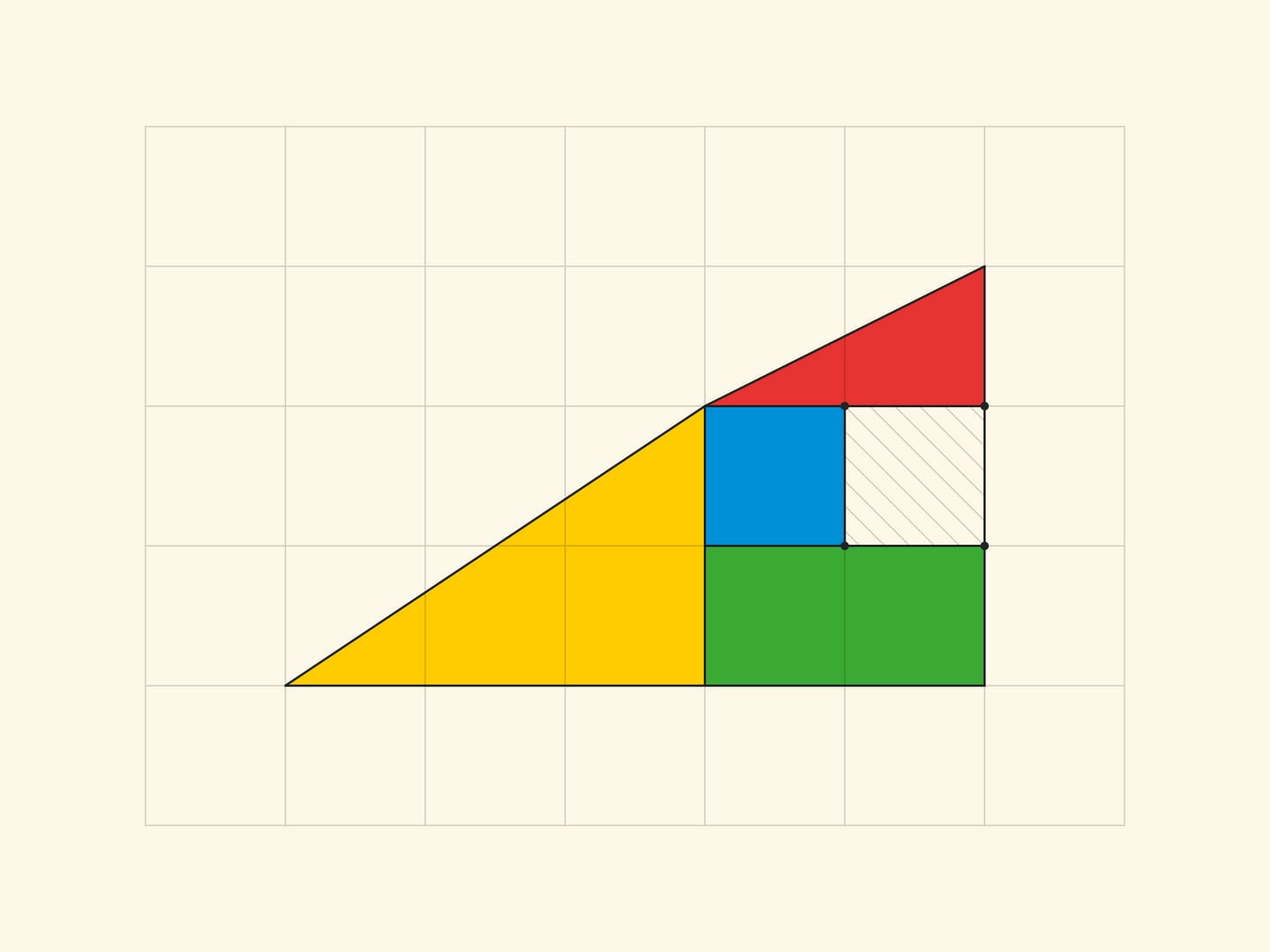
All the vertices of all the parts lie in the nodes of the square grid. And it is easy to make sure that the borders of the parts do not add up in a straight line, but form the sides of a parallelogram (with vertices in the nodes) by counting the slope of each segment by the cells. In the rectangle $5\times 13$, in the yellow triangle the ratio of the cathetuses is $\tg \alpha=\dfrac{3}{8}$, and for the blue trapezium the tangent of the “same angle” is $\dfrac{2}{5}$. For the triangle sophism: in Gardner’s variant $\dfrac{2}{5}\ne \dfrac{3}{8}$, in the smaller version $\dfrac{1}{2}\ne \dfrac{2}{3}$. In all cases the sides of the parallelogram are, as they should be, pairwise equal and parallel. The vertices of the parallelogram lie in the nodes of the grid, but there are no nodes inside the parallelogram. Which, however, is not surprising, if we remember that the area is equal to one and the Pick’s formula.
Having solved the inconsistency, let us think how to construct such sophisms. We may notice that the numbers encountered, $1,$ $2,$ $3,$ $5,$ $8,$ $13$, are the beginning of the famous sequence of Fibonacci numbers
$ \{1,$ $1,$ $2,$ $3,$ $5,$ $8,$ $13,$ $21,$ $34,$ $55,$ $89,\ \dotso\}.$
This sequence is given by the recurrence relation $$ F_n=F_{n-1}+F_{n-2} $$ and a pair of prime numbers $F_0=1$, $F_1=1$.
There are many interesting relations between the Fibonacci numbers. In the year $1680$ a French astronomer of Italian origin, Giovanni Domenico Cassini, who discovered the satellites of Saturn and a gap in its rings, noticed this relation: $F_{n+1}\cdot F_{n-1}-F_n^2=(-1)^n$, which now goes by his name.
When $n=6$ the equation obtained is $5\cdot 13-8^2=1$ — the familiar numbers from “The Chessboard Paradox” and the familiar increase by one! But to take a Fibonacci number with an odd number as a side of the square is impossible — the parts can be added to the corresponding rectangle only with an overlap (the intersection is still the same parallelogram of unit area).
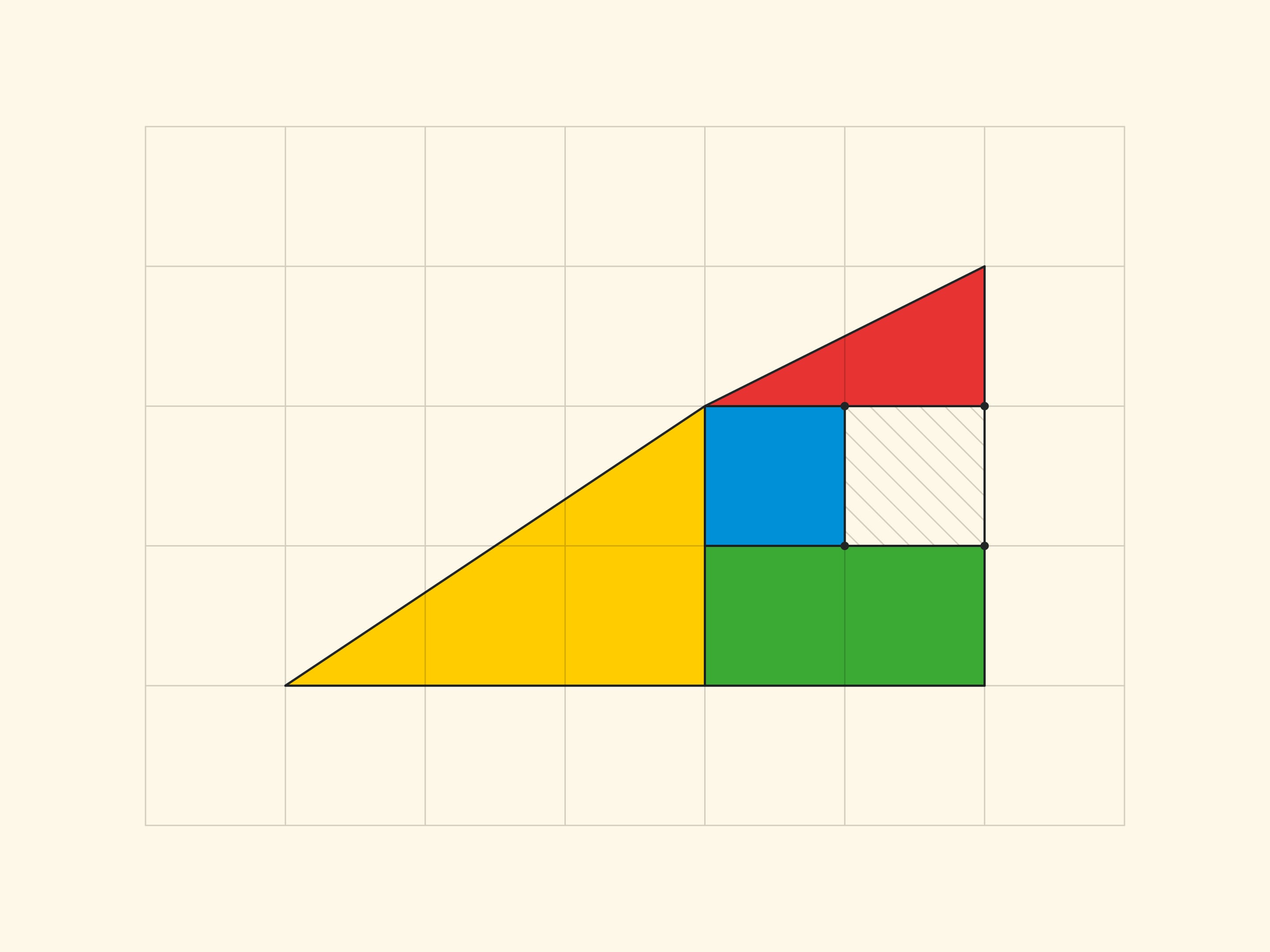
In the “Gardner triangle” the cathetates of the small (real and not changing area) triangles are Fibonacci numbers: the red one has 3 and 8, the yellow one has 2 and 5. Correspondingly, the sides of the rectangle (in which the increase per cell occurs) are: before rearrange, 3 and 5, and after rearrange, 2 and 8. The increase in the area of the rectangle per cell provides the ratio by four consecutive Fibonacci numbers: $F_{n}\cdot F_{n-3}-F_{n-1}\cdot F_{n-2}=(-1)^n$, which can be obtained from the Cassini relation and the recurrence relation. For $n=6$ the resulting equality is $8\cdot 2-5\cdot 3=1$, on which the “Gardner triangle” relies.
Thus sophisms are built on the fact that the sizes of figures and parts of which they are composed are several consecutive Fibonacci numbers. On the basis of these relations we can construct similar sophisms for figures of larger sizes. In Loyd’s variant one should not forget about parity, and in Gardner’s variant, if one wants to make the square gather into a square cell, one should increase the number of parts of which the basic rectangle is made up.
For Fibonacci numbers there is also an explicit, not recurring, assignment, called the Binet formula: $$ F_n=\frac{1}{\sqrt{5}}\Big(\frac{1+\sqrt{5}}{2}\Big)^n-\frac{1}{\sqrt{5}}\Big(\frac{1-\sqrt{5}}{2}\Big)^n. $$ Note that although Fibonacci numbers are integers, there is an irrational number in the formula for them — the golden ratio $\phi=\dfrac{1+\sqrt5}2$.
The first parenthesis in the Binet formula equals nearly $1{,}618$, and the second parenthesis is a negative number and modulo less than one (approximately $-0{,}618$). So the Fibonacci numbers are rapidly increasing, or, more precisely, $F_n\sim\dfrac1{\sqrt5}\varphi^n$. This explains why as the slit in the form of a parallelogram gets narrower and narrower and more difficult to notice (compare for example the small and large “Gardner triangles”). Indeed, the slopes of different segments in sophisms have the form $\dfrac{F_{n+2}}{F_n}$, and as $n$ grows these relations become closer and closer to $\phi^2$ and practically indistinguishable.
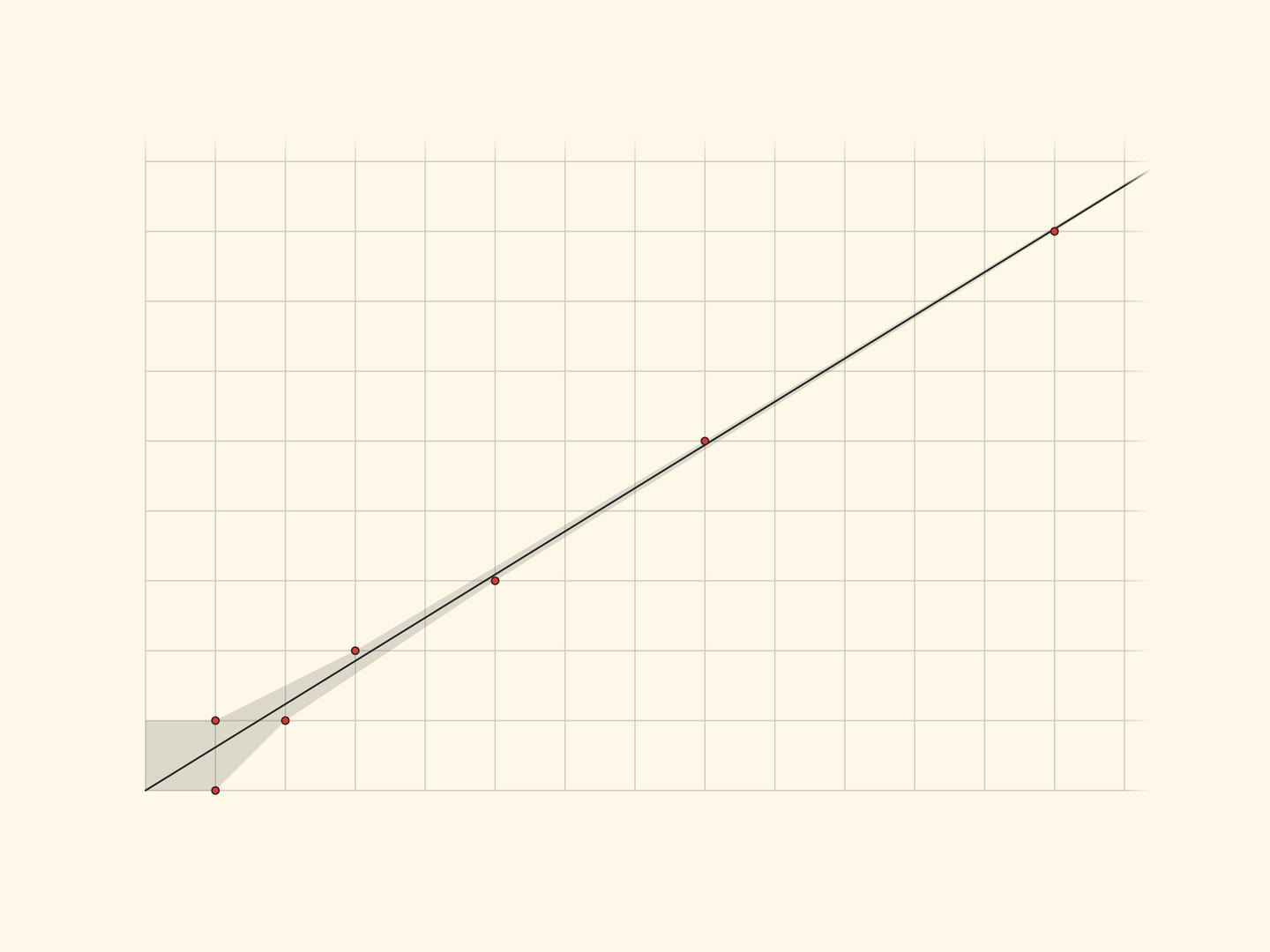
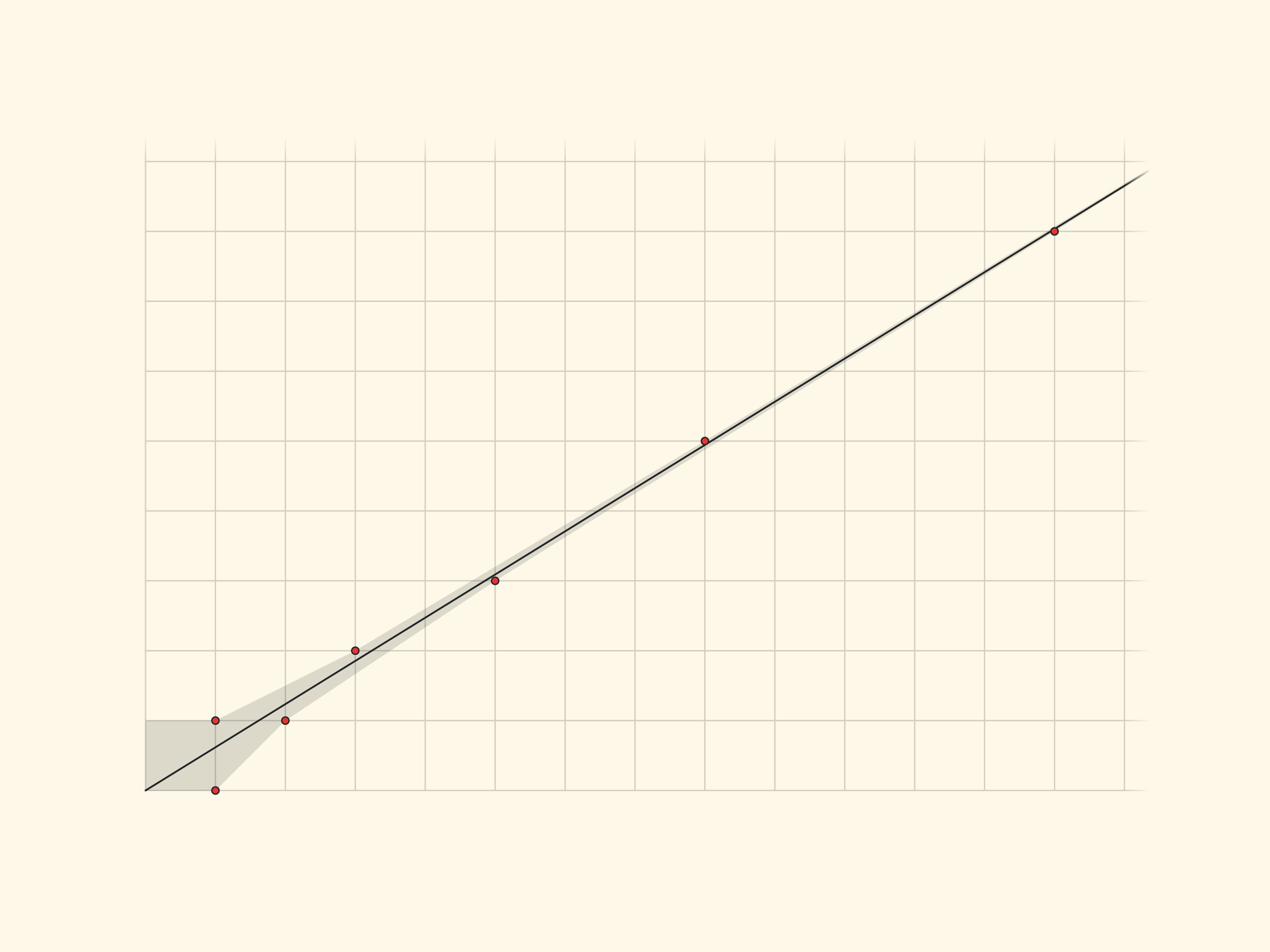
The unit parallelogram and its diagonal are the objects of a beautiful science begun by Hermann Minkowski — geometry of numbers. More precisely, geometric interpretation of chain fractions.
The figure shows the $x=\dfrac{1+\sqrt{5}}2y$ line and marks the nodes of the grid closest to it. Their coordinates are adjacent Fibonacci numbers, and the points themselves, jumping one after another above and below the line, approach it. And the relations of neighbouring Fibonacci numbers give in some sense the best rational approximations to the Golden Section... The reader, intrigued, may refer to the brochure “Chain Fractions” by Vladimir Igorevich Arnold.
It may seem just a trick, just a picture, walking around the Internet… But they contain so much non-trivial mathematics!