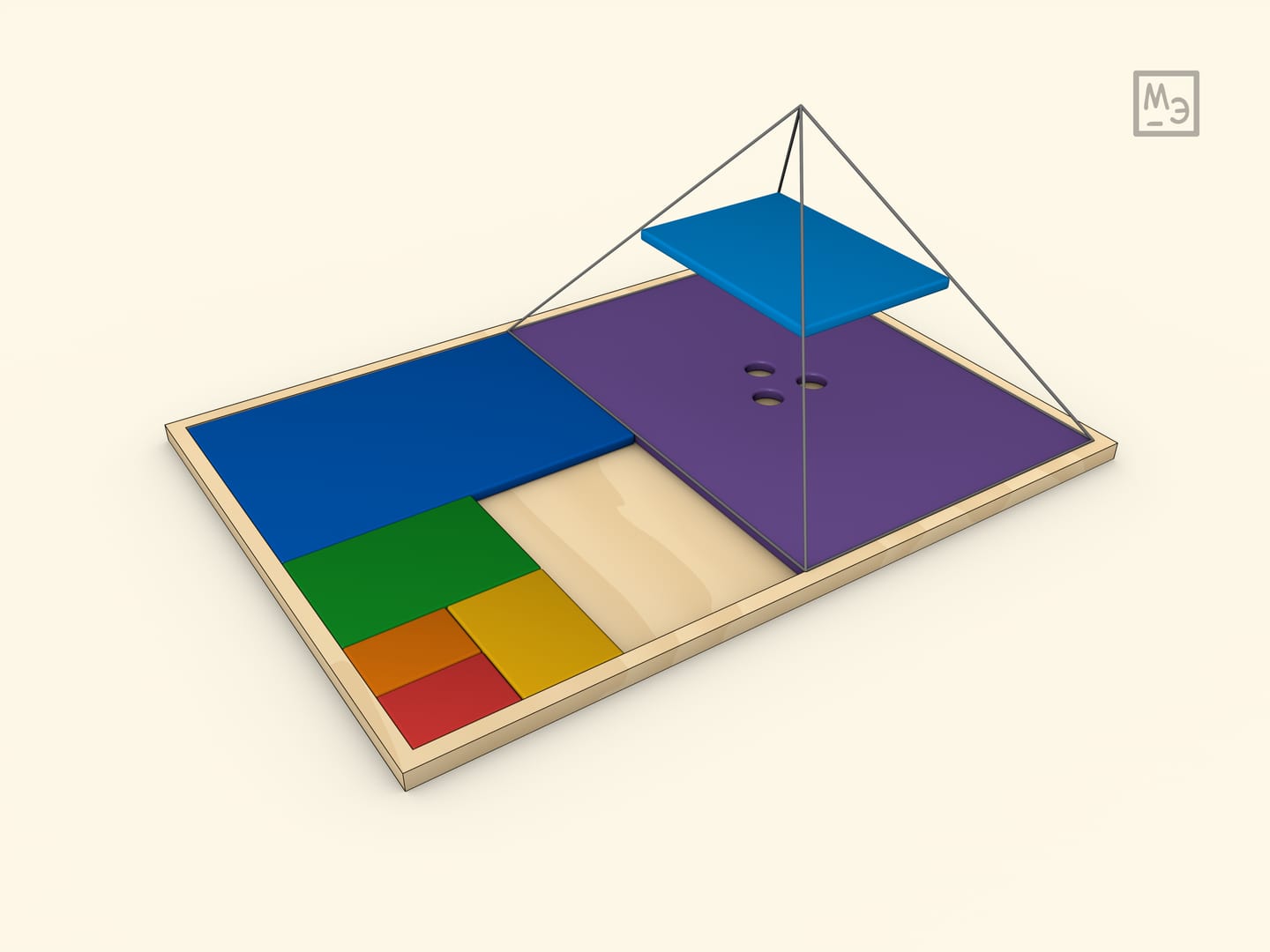
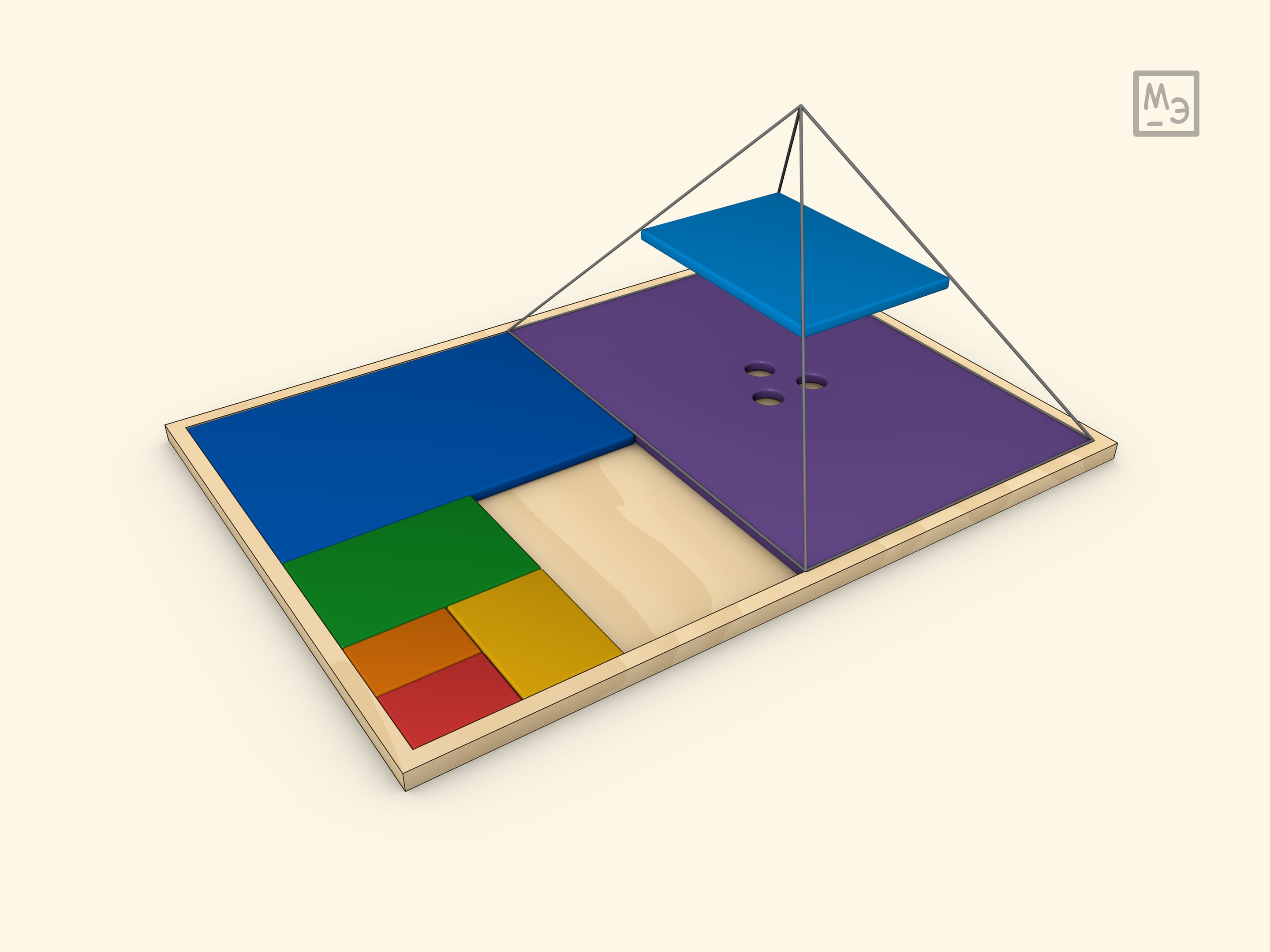
The sum of an infinite geometric progression is equal to $b_1/(1-q)$, where $b_1$ — the first term of the progression, and $q$ — its common ratio ($|q|<1$). When $q=1/2$, the sum can be “calculated” geometrically.
If we take the area of the larger part as 1, then the sum of the areas of all parts obviously equals 2.
If the field is not arbitrary, but has an aspect ratio of $\sqrt{2}$, then all the resulting parts, when divided in half, will be similar to each other.
The model can be made of wood or cardboard. For secondary school pupils it can serve as an illustration of both the sum of an infinite geometric progression with a common ratio of $1/2$ and the sum of powers of two. And for younger students — a puzzle.