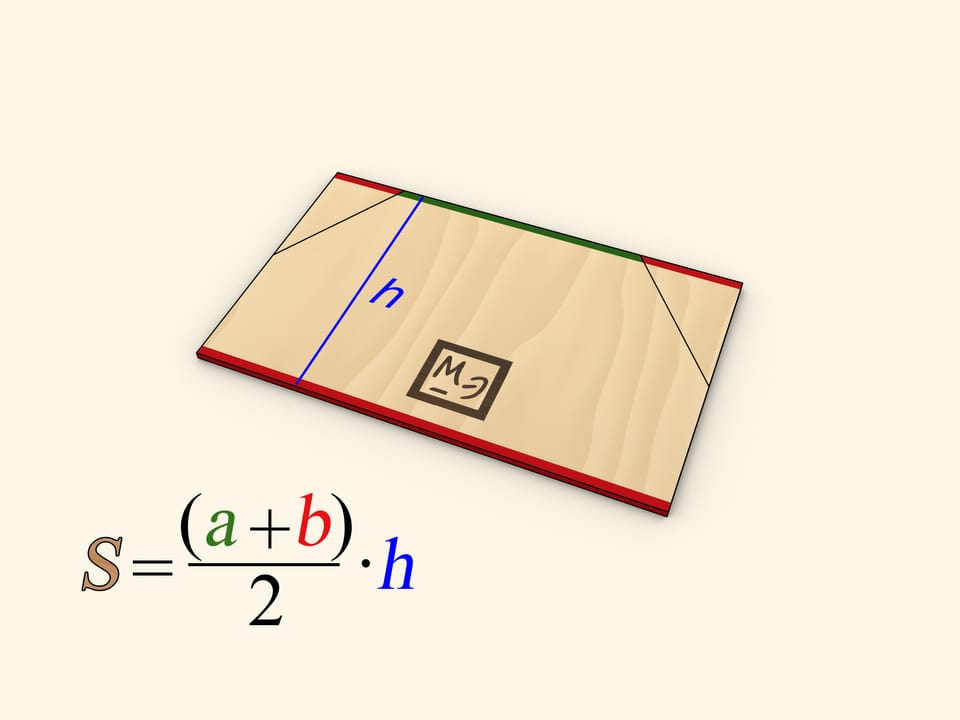
Area of a trapezoid with bases of lengths $a$ and $b$ and of height $h$ equals $S=(a+b)/2 \cdot h$. One can make sure of that using the formula for the area of a triangle. To achieve it, the trapezoid should be cut into several pieces that can be rearranged to form a triangle or rectangle.
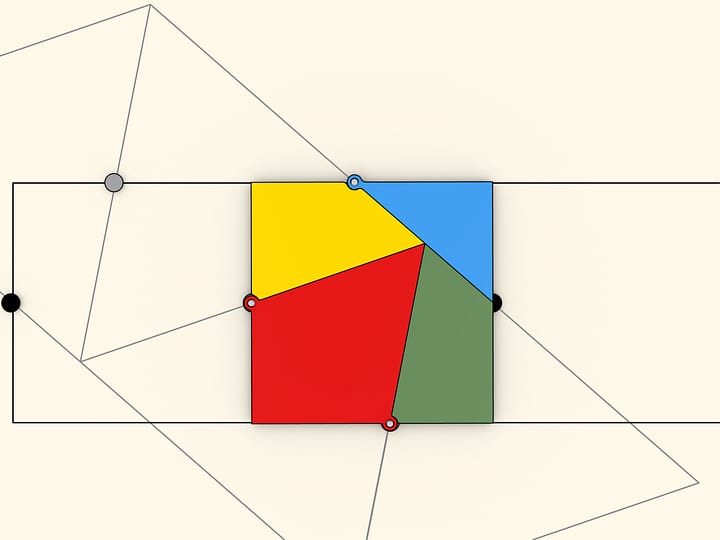
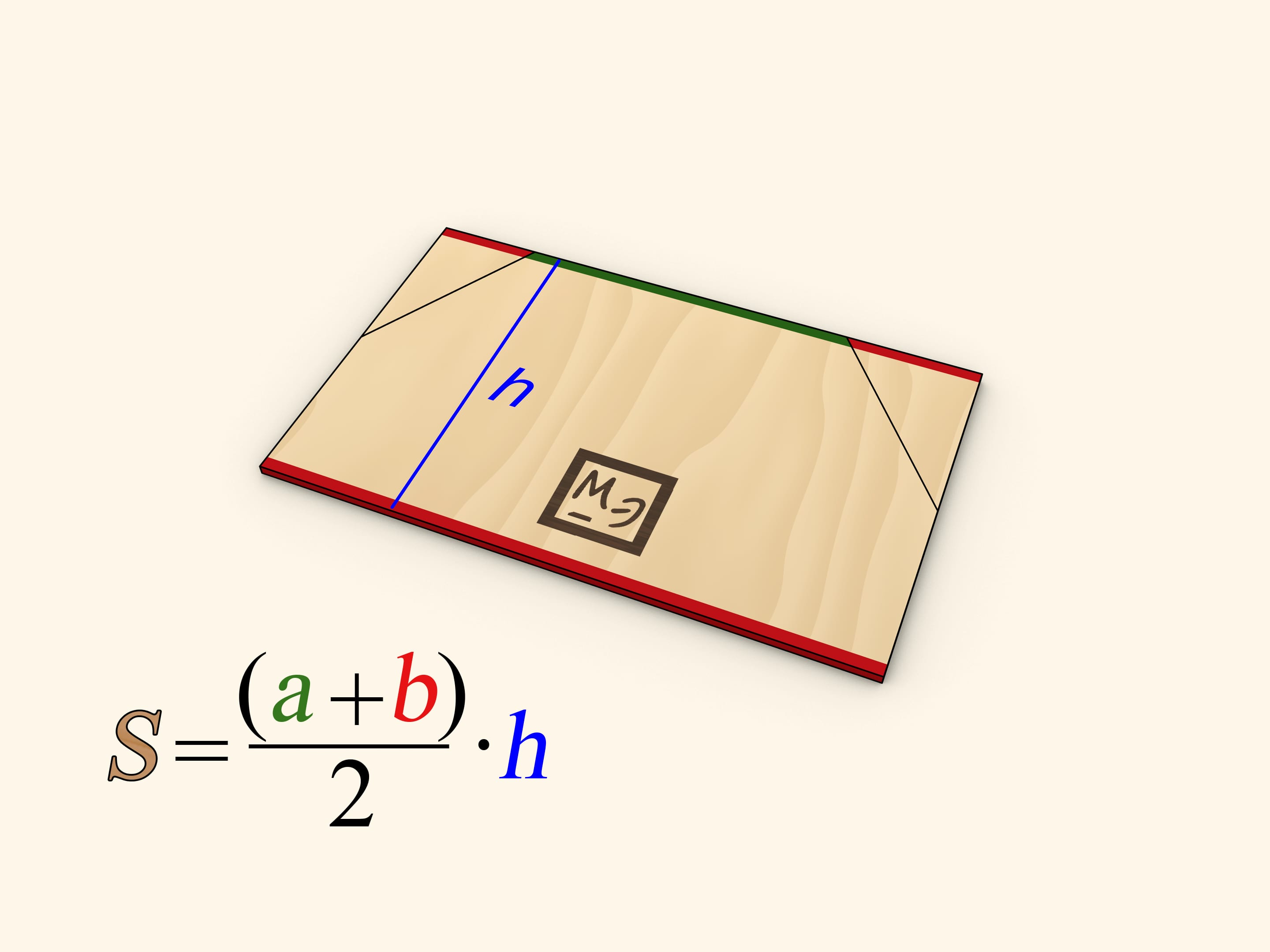
This formula can be illustrated using the formula for the area of a rectangle. Drop the altitudes to the longer base at the midpoints of trapezoid's legs and then cut the trapezoid along the altitudes. Attach the two cut off right triangles's hypothenuses to the remaining parts of the legs. The shape obtained is a rectangle.
One of the rectangle's sides is as long as $h$ — the trapezoid's height. Sum of two other sides' lengths equals sum of the trapezoid's bases' lengths, thus one side is as long as half of that sum, that is $(a+b)/2$. So the triangle's area, and so the area of the initial trapezoid, equals $ S = (a+b) / 2 \cdot h$.
To prove that completely one still should make sure that the shape obtained after rearranging the triangles is indeed a rectangle — each short side and each composed long side is a line segment, and the corresponding lines are parallel. The fact that the angles obtained are right is provided by the cutting method itself — cuts are made along the altitude perpendicular to the base.
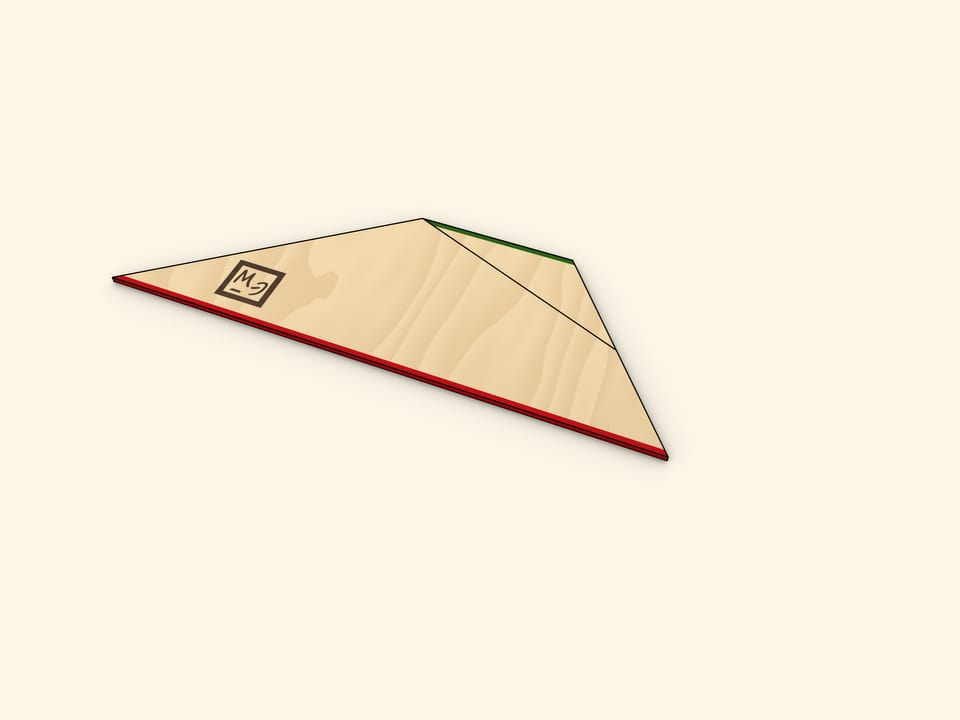
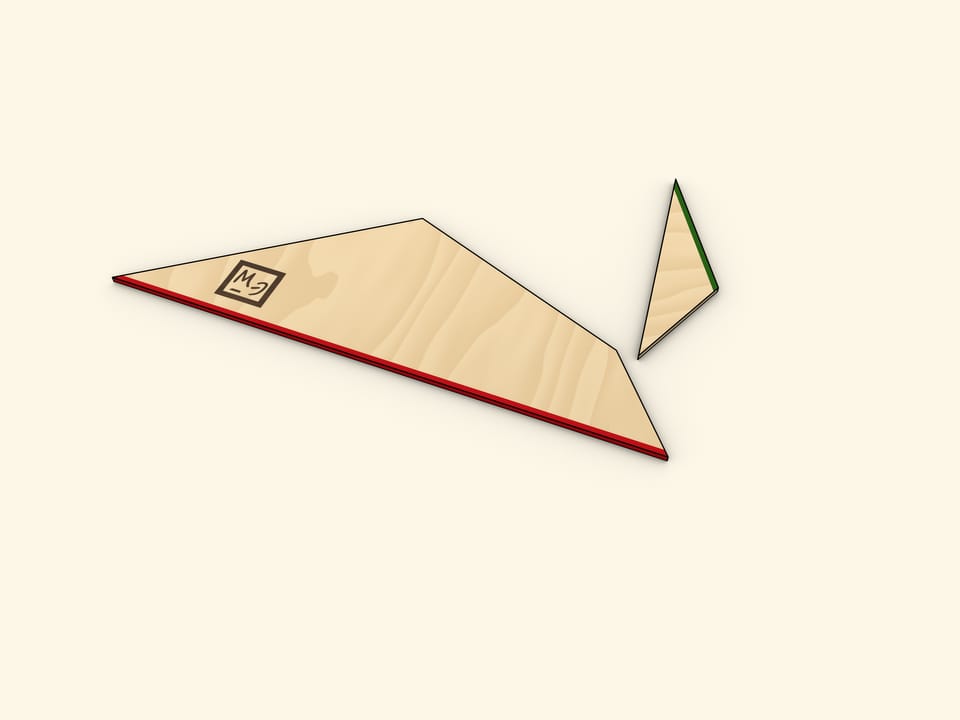
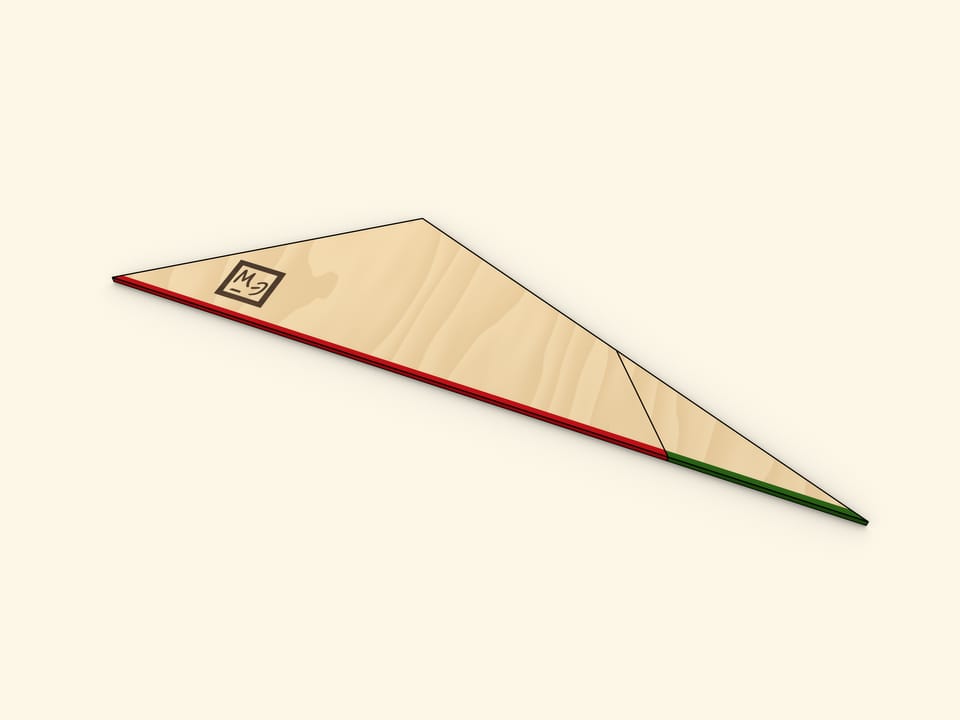
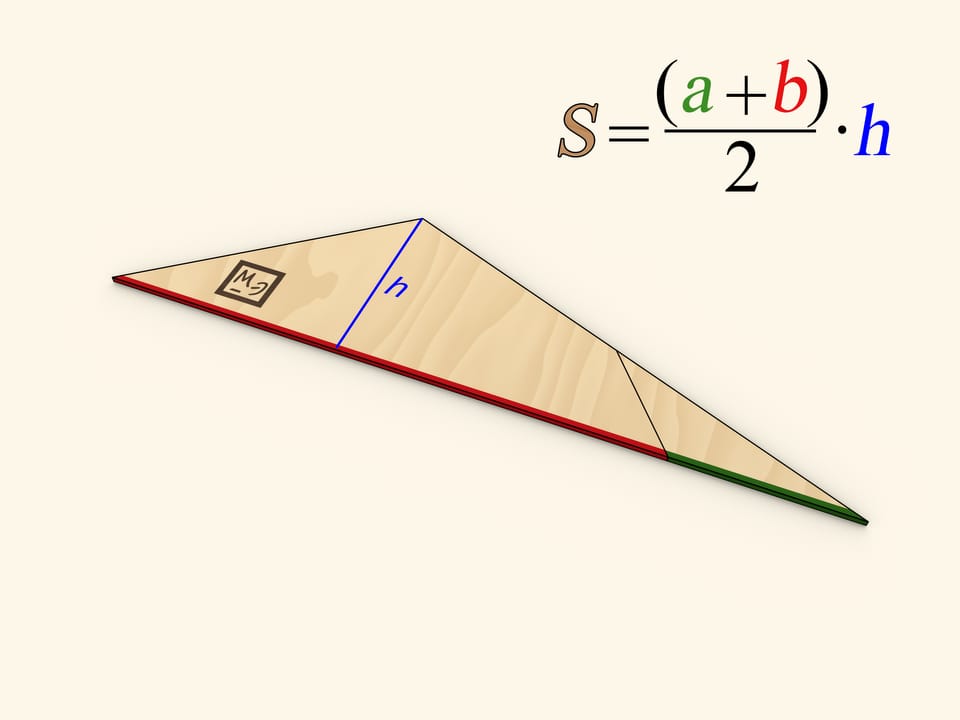
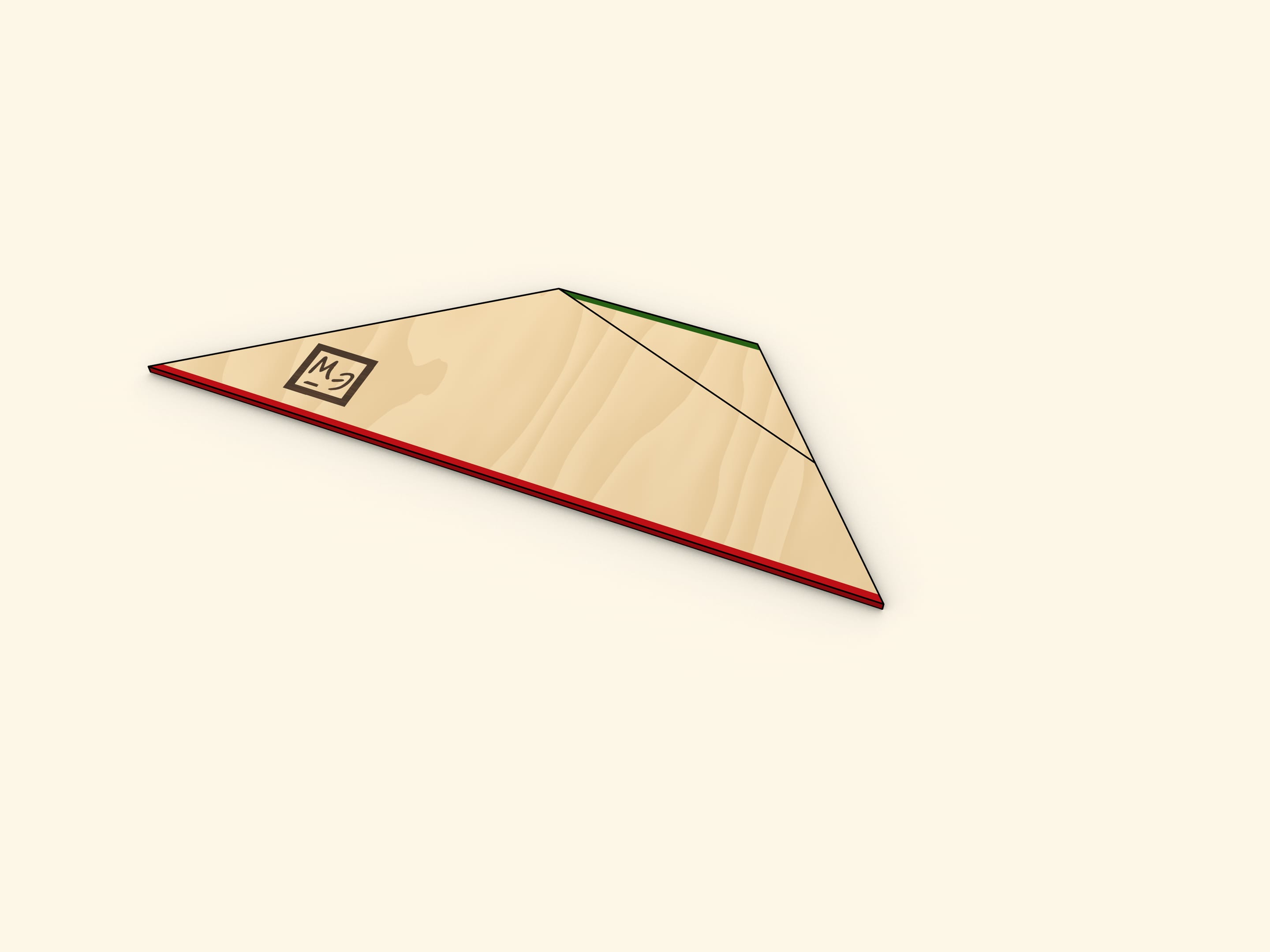
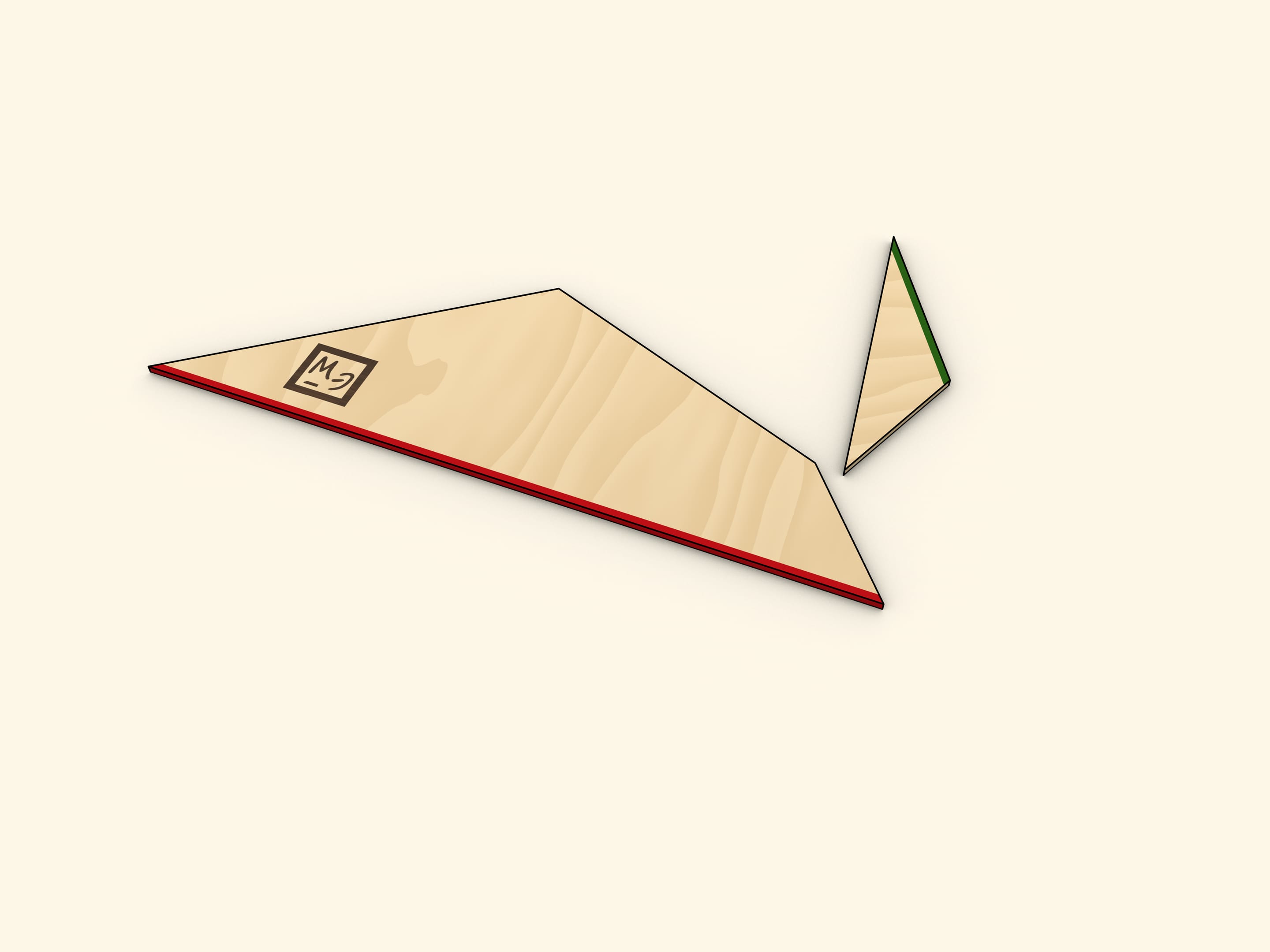
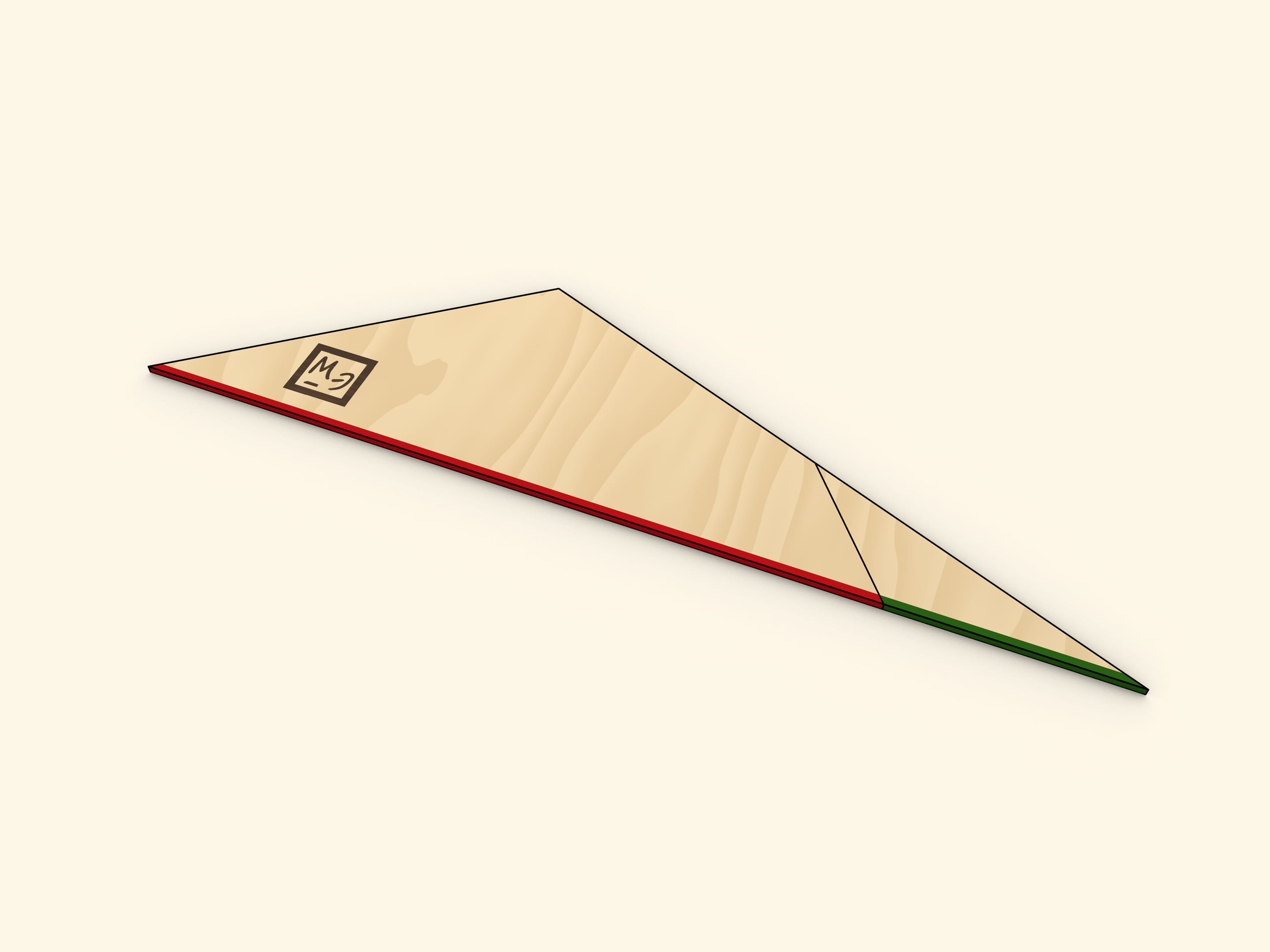
Cut the triangle along the line connecting its vertex with the midpoint of the opposite side. Rotate the cut off triangle up to a moment when both bases of the trapezoid are along the same line. Make sure that in this the two halves of the cut side also lie on the same line, so indeed that forms the triangle.
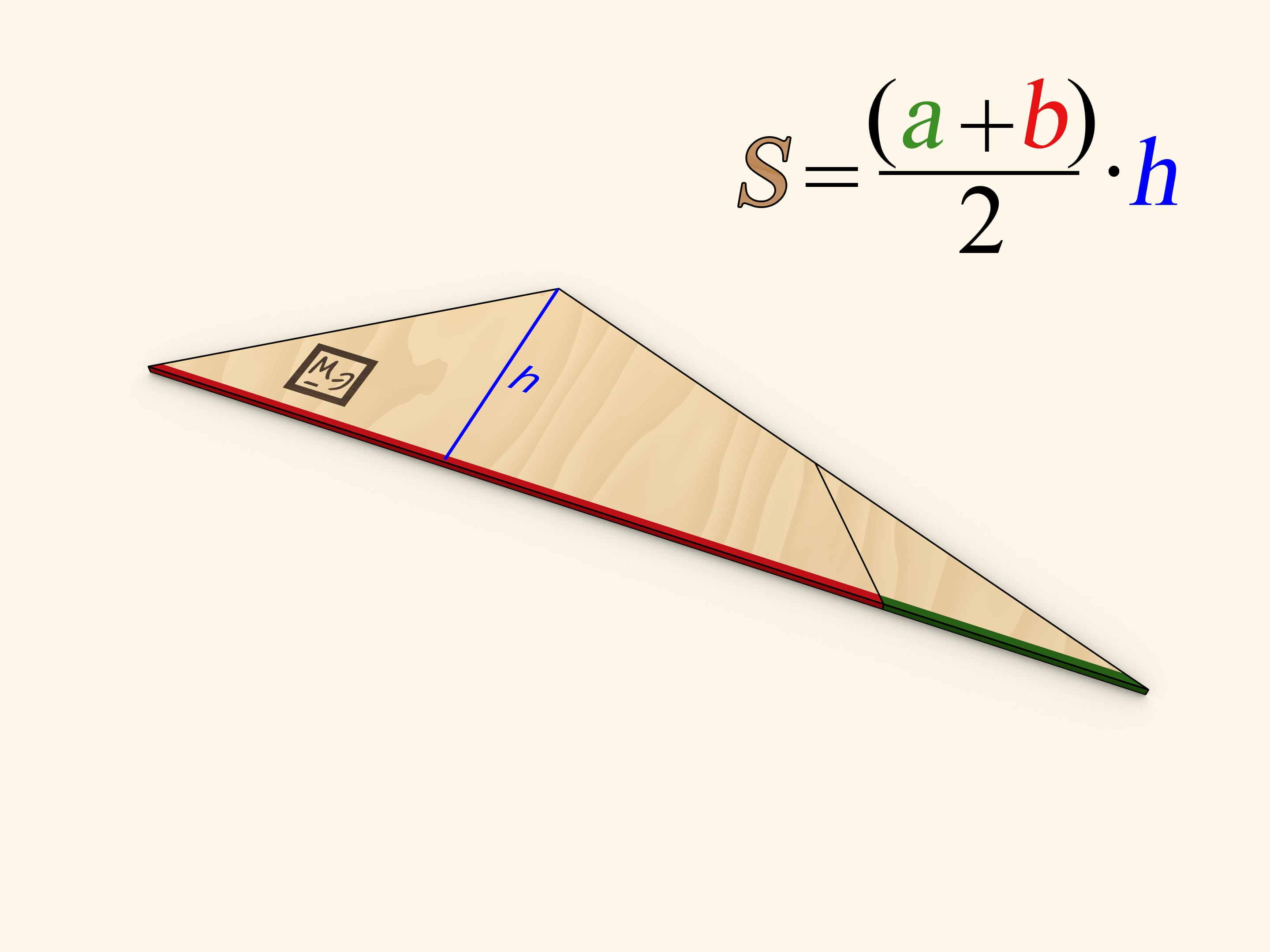
One of the sides of the triangle obtained is as long as the sum of trapezoid's bases' lengths, and the altitude dropped at that side is as long as the trapezoid's height.
One of the methods of finding the area of a triangle is finding the half of a product of a side length and the length of an altitude dropped at that side. Using this method gives the familiar formula for the trapezoid area.
Both models can be built from an approximately 10 mm thick wooden board. For the convenience of demonstration, the two parts it was cut into can be attached together with the help of magnets.