Cubism — a nonobjective school of painting and sculpture developed in Paris in the early 20th century, characterized by the reduction and fragmentation of natural forms into abstract, often geometric structures usually rendered as a set of discrete planes.
The American Heritage Dictionary of the English Language: Fourth Edition. 2000
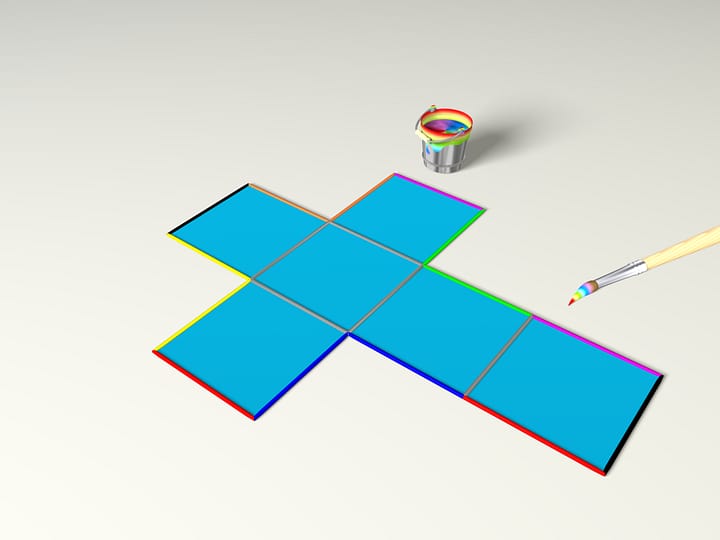
In how many ways can we cut a cardboard cube along the edges so that we can place the resulting parts on a plane. In geometric language, how many nets does a cube have?
It turns out that there are eleven. Think up a proof of the fact that there is no more and we will show you all of them in our cartoon.
It's interesting that any of them can be used to parquet your room. In order to do that we have to place planks without overlaps and so that every single point is covered.
Every time we'll prove it in the following way. First we construct an infinitely long (in one direction) stripe (sometimes with smooth, but generally with uneven border). Then we mention that a copy of the stripe can be placed closely to the first one and repeating this construction we can fill the whole plane.