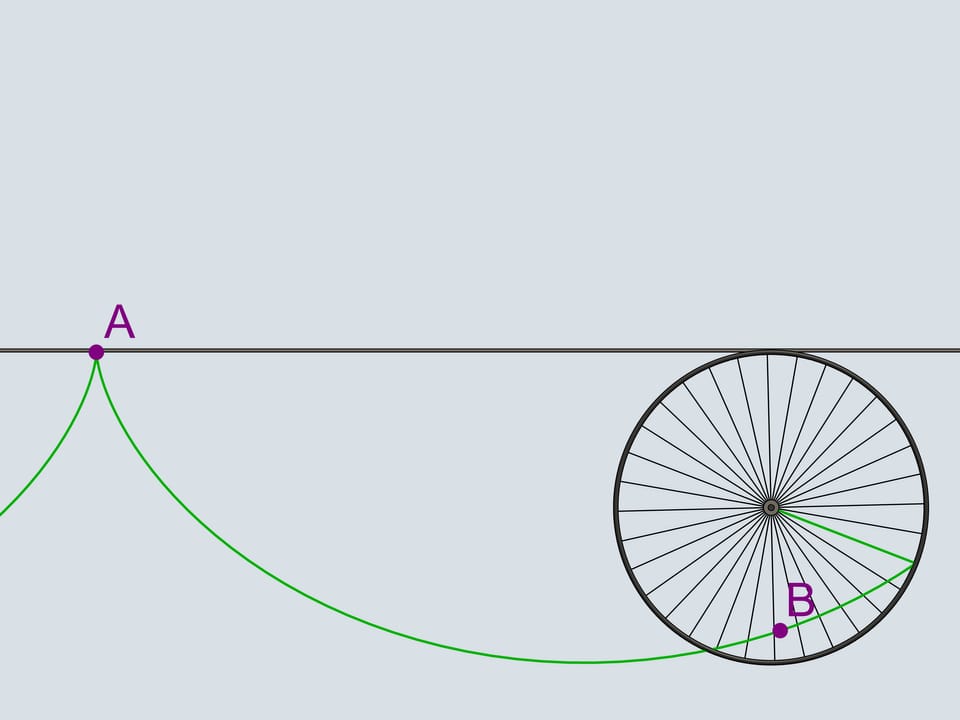
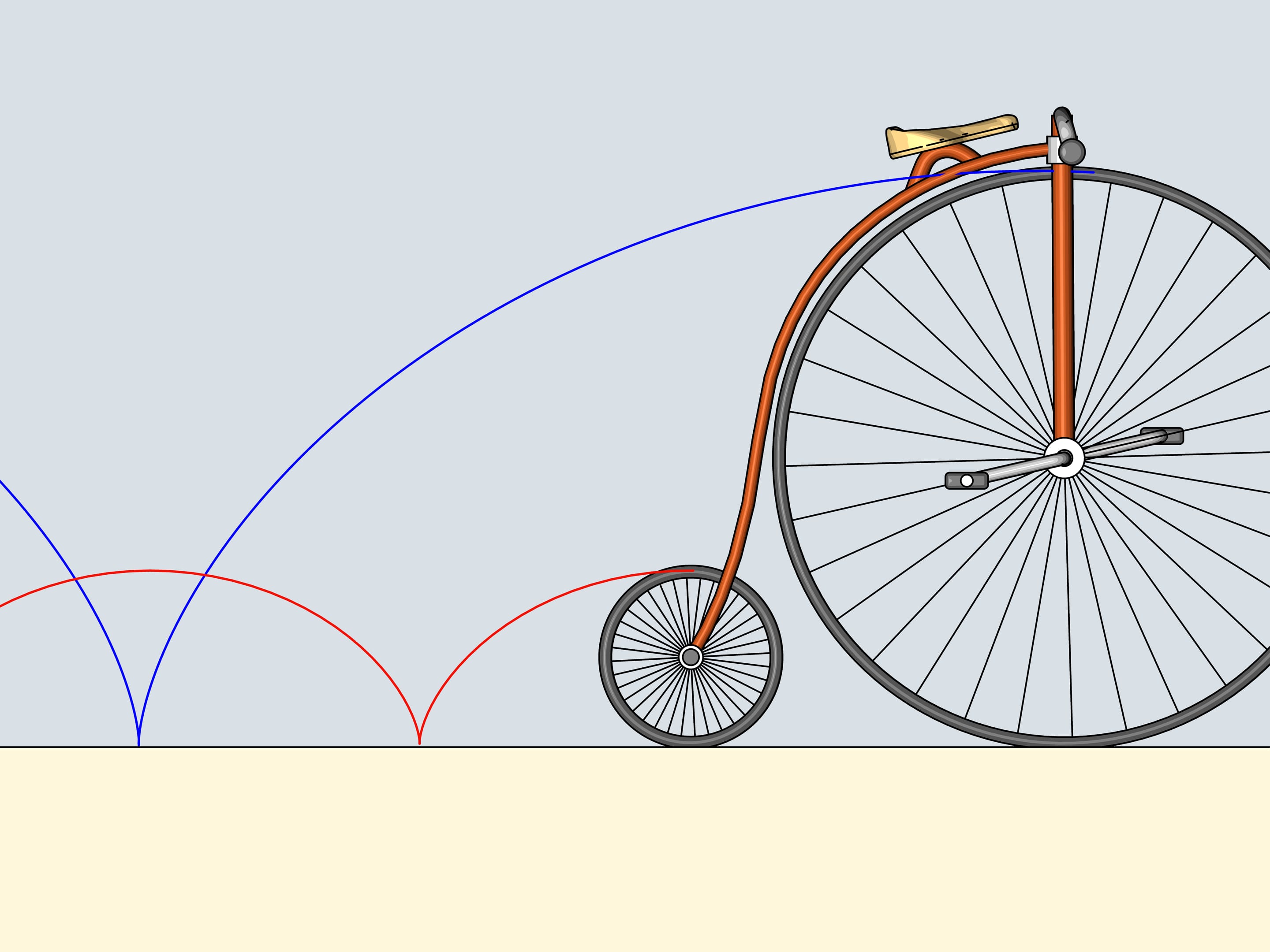
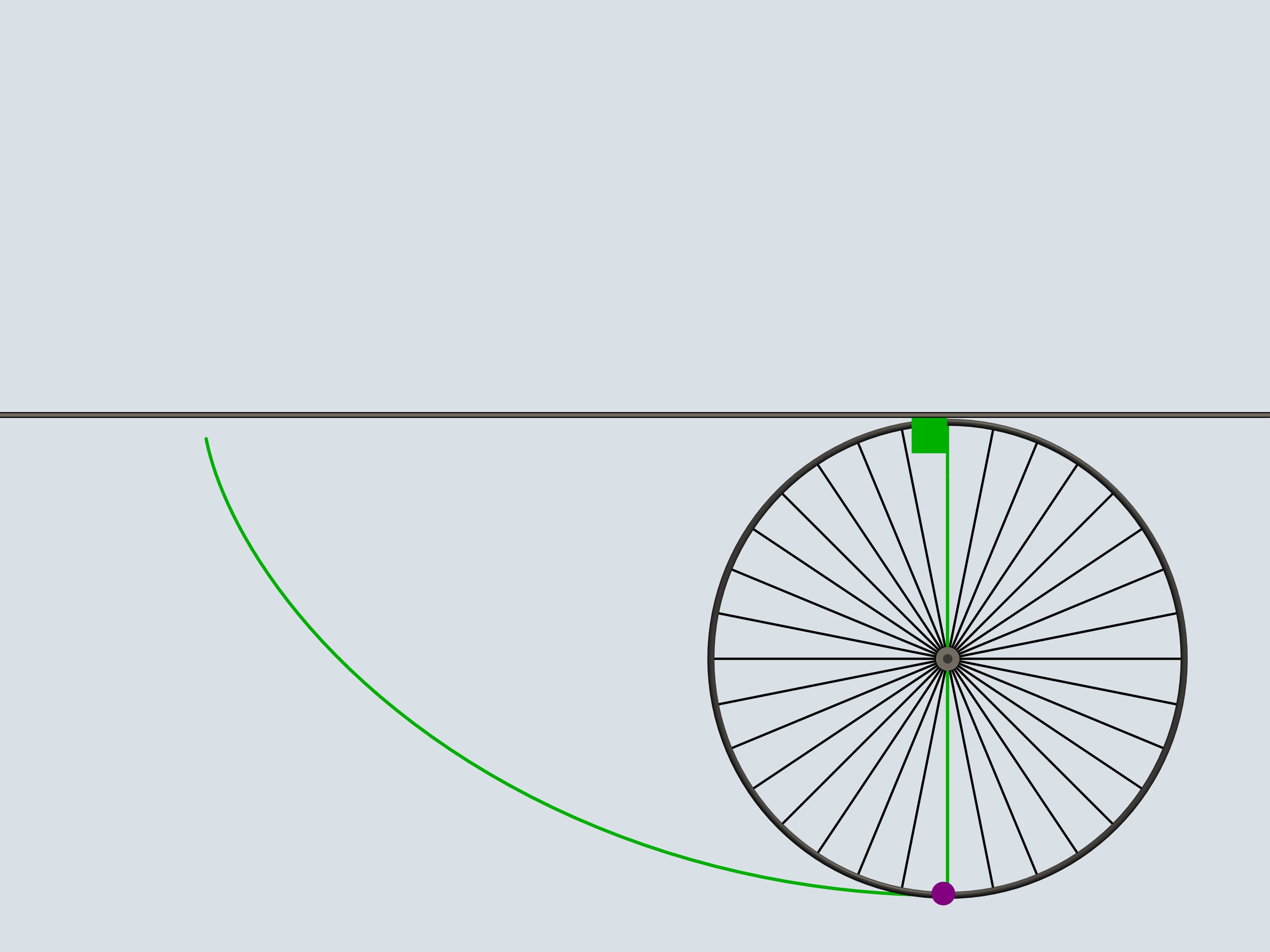
Do you remember plastic cat's eyes, light reflectors that we attach to the bicycle wheels? Attach one adjoining the border of the wheel and follow its trajectory. The curves we obtain belong to the family of cycloids.
The wheel is the cold the generating disk (or circle) of the cycloid.
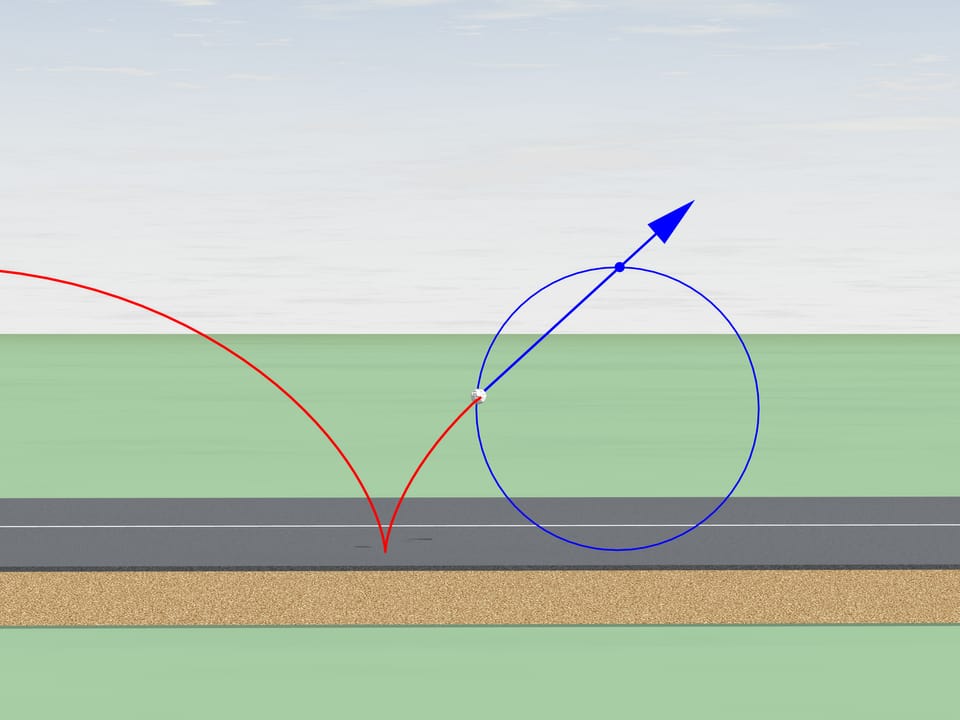
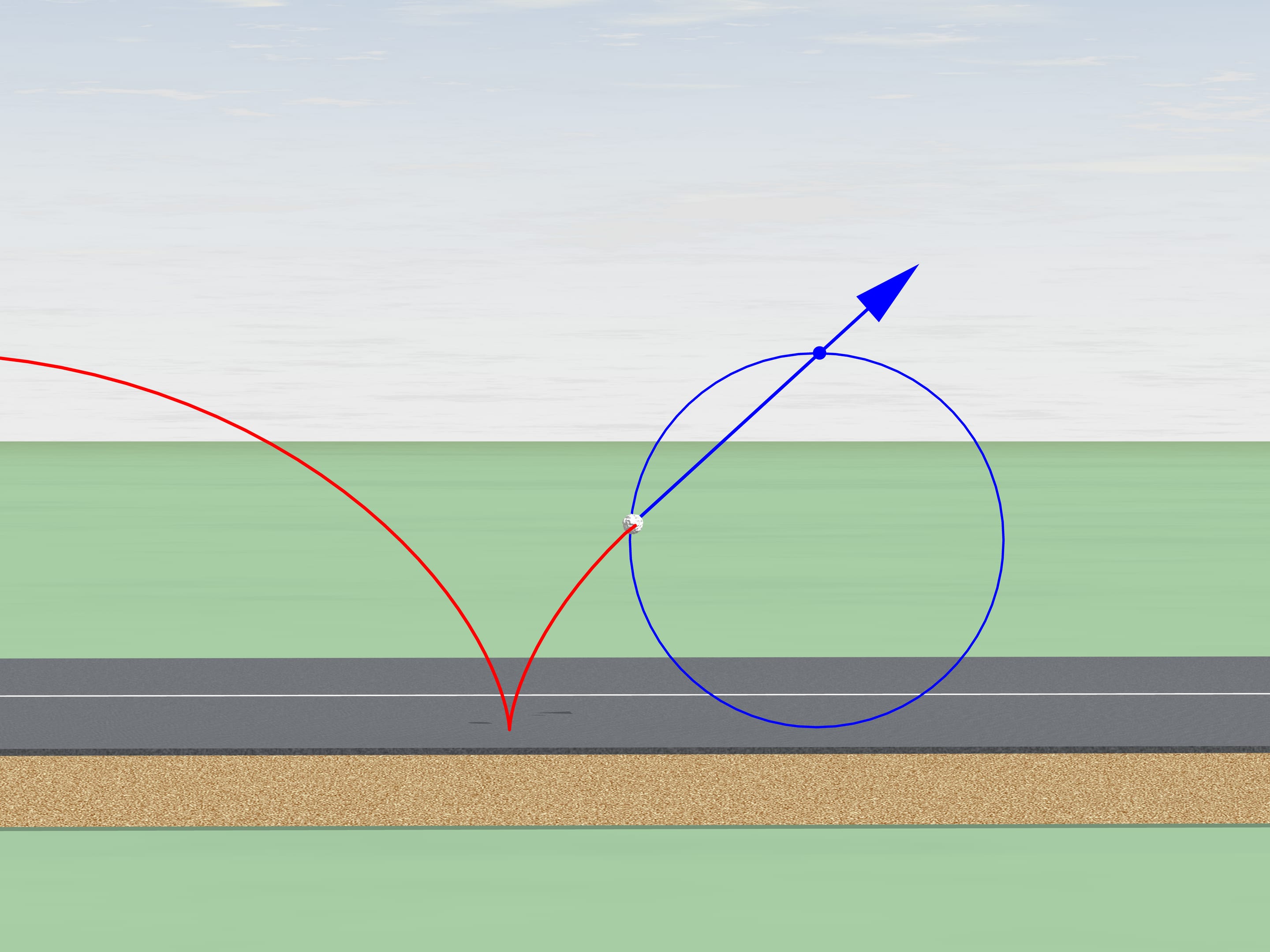
But let's return to our century and take use modern technique. There is a stone on the bikes way that got stuck in the wheels tread. In what direction will it fly after several turns when it leaves the tread? In the direction of the bike or in the opposite?
As we know, the motion should start tangent to its old trajectory. A tangent to a cycloid has always the same direction as the bike and passes through the top point of the generating circle. It will fly in the same direction.
Do you remember driving your bicycle over the puddles without a back wing in your childhood? A wet stripe on your back was an every-day confirmation of this result.
The XVII century is the century of the cycloid. The best scientists were studying its properties.
Which trajectory moves a body with gravitation acting on it for one point to another in the shortest time? This was one of the first problems of the branch of science which is now called variational calculus.
One can minimize (or maximize) different parameters: the length of a path, speed, time. The problem of brachistochrone is to minimize time (which is accentuated by the name: brachistos means the shortest, and chronos means time in Greek).
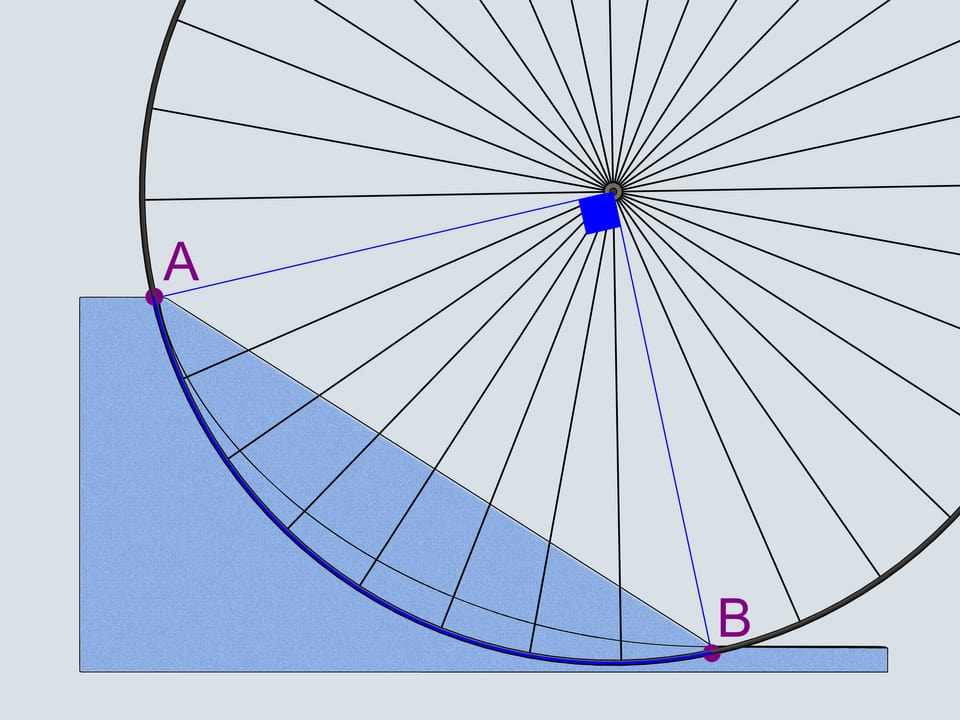
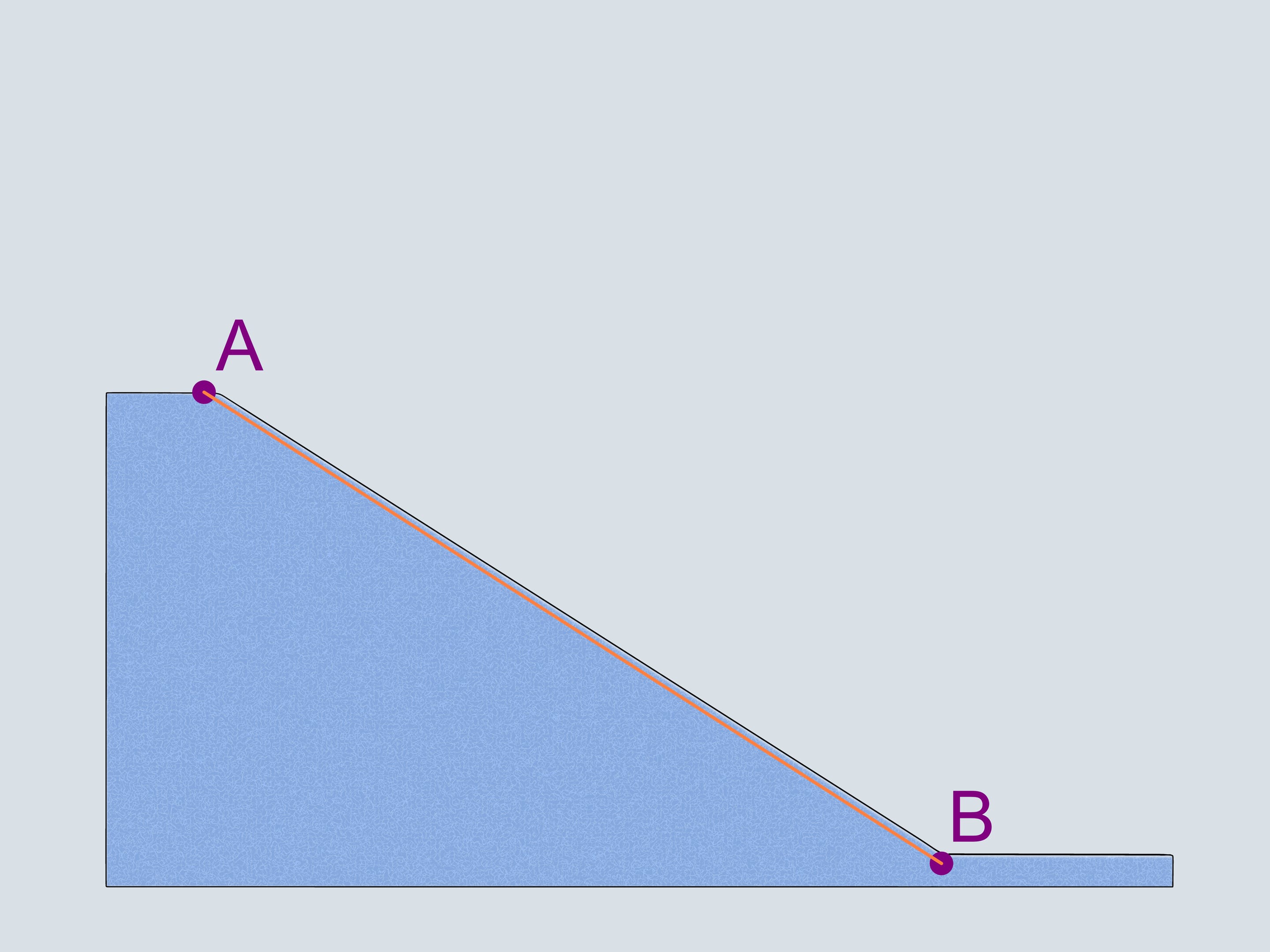
The first that comes to mind is a straight-line trajectory. Let's also consider a reversed cycloid with the cuspidal point in the upper of two given points. And, following Galileo Galilei, a — quarter of a the circle connecting our points.
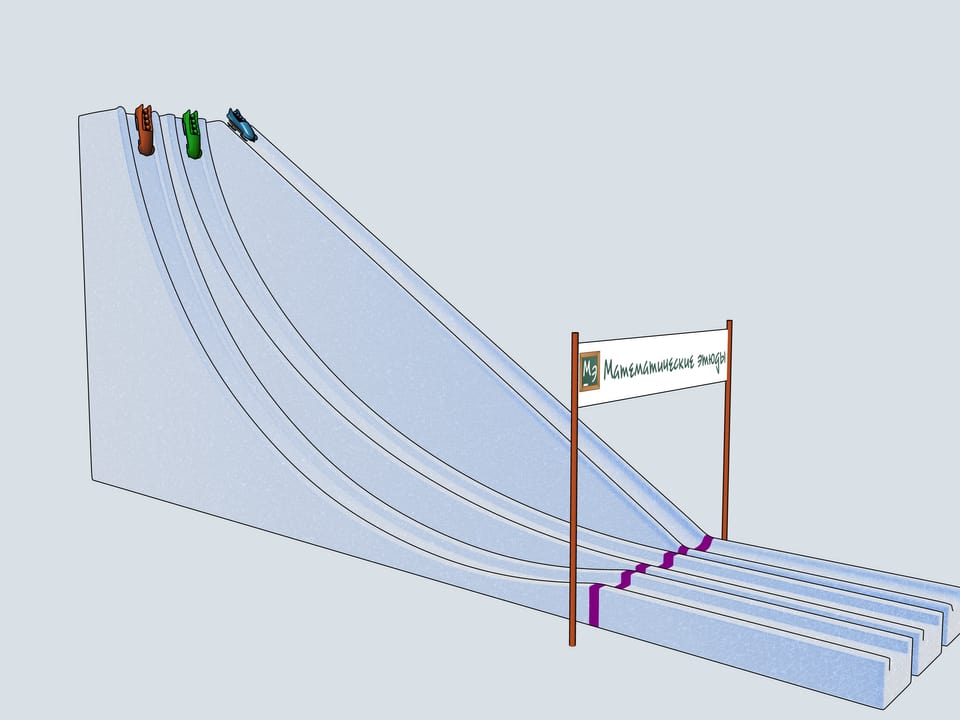
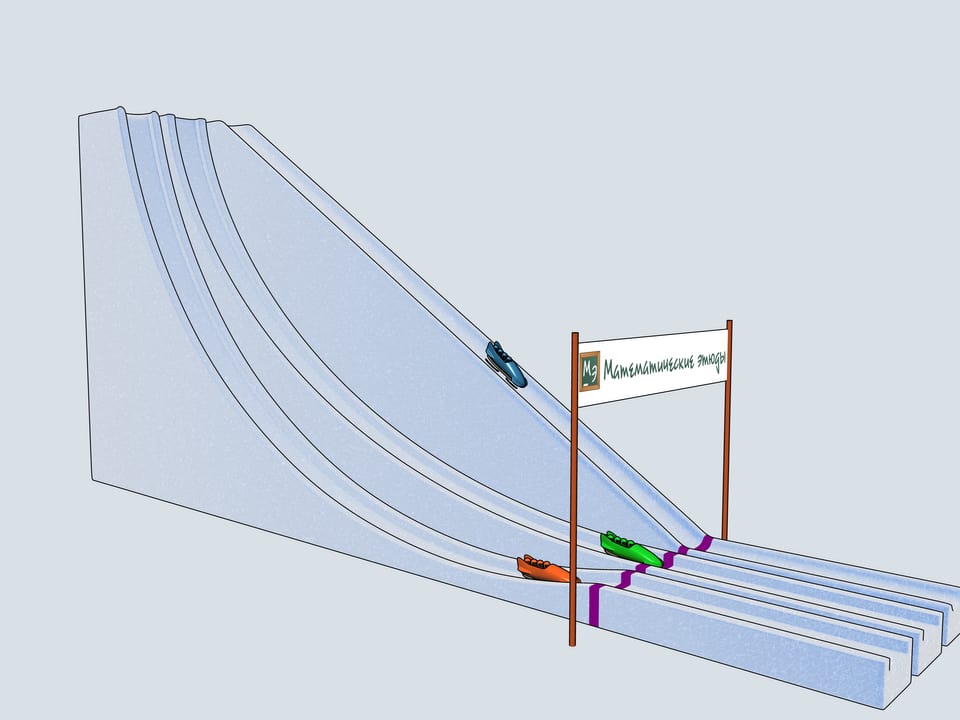
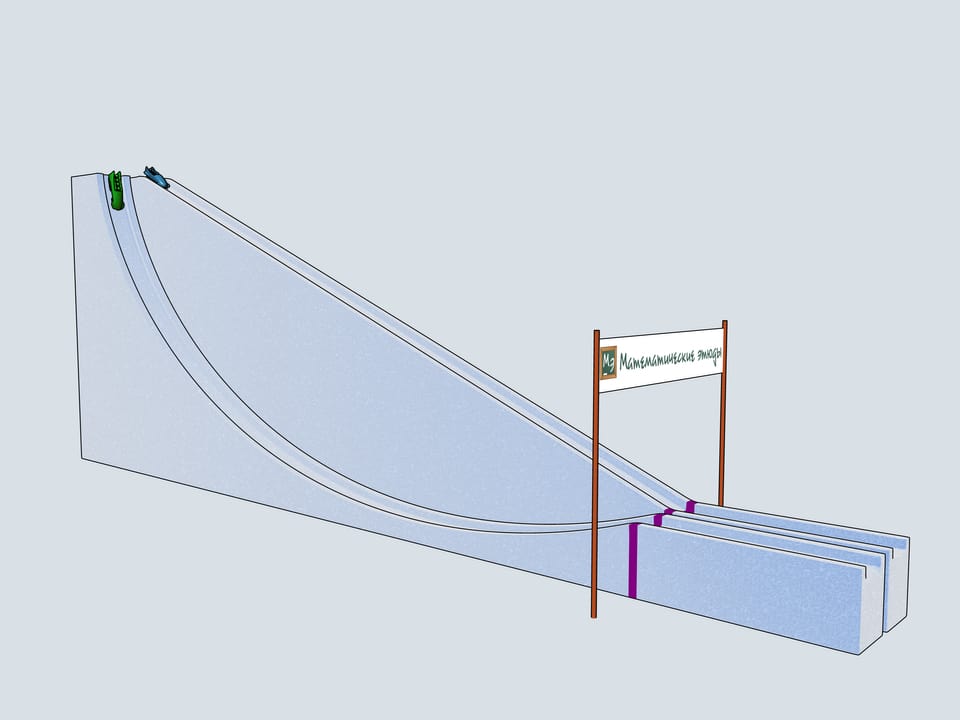
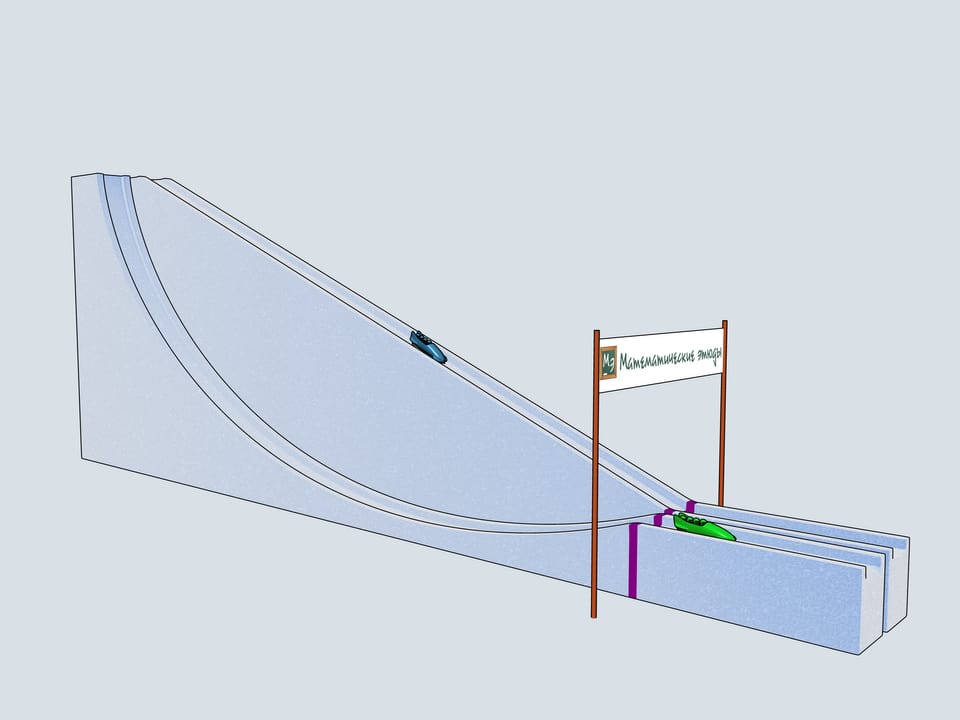
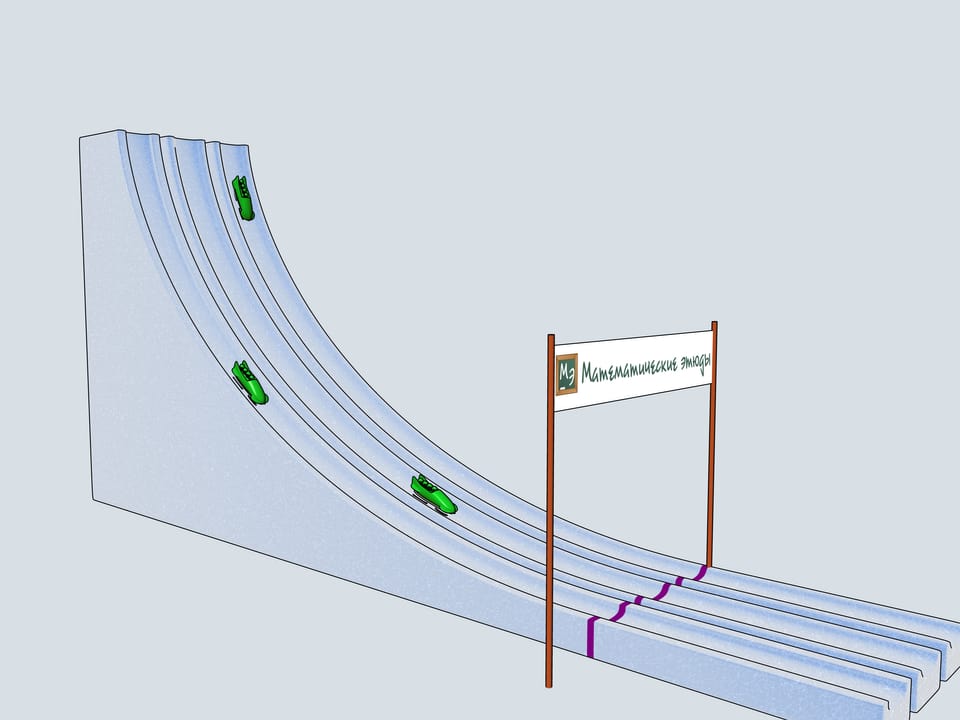
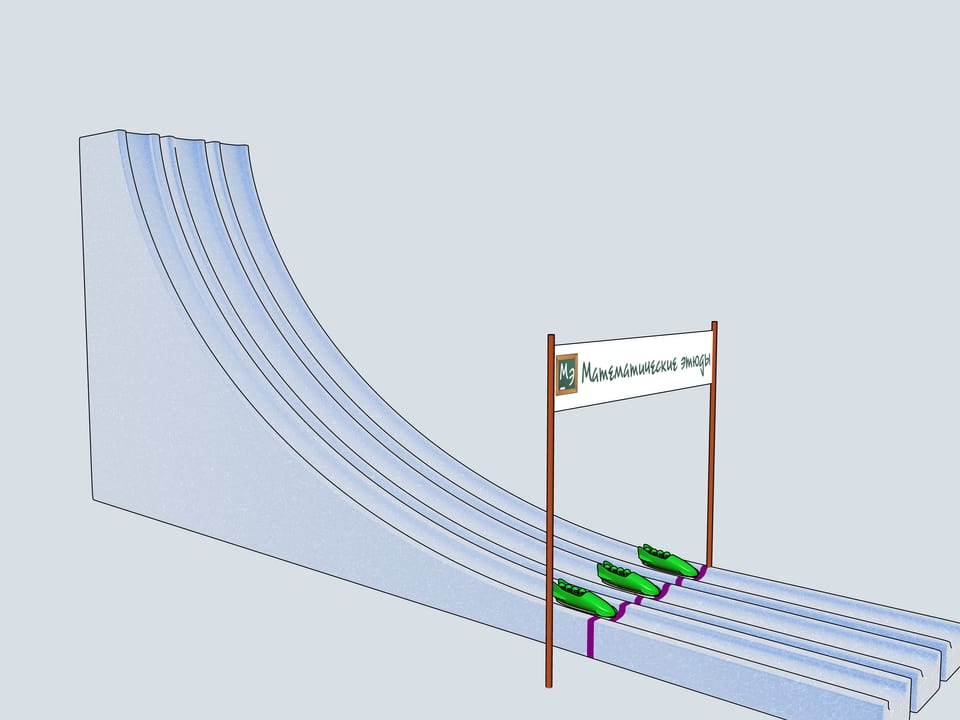
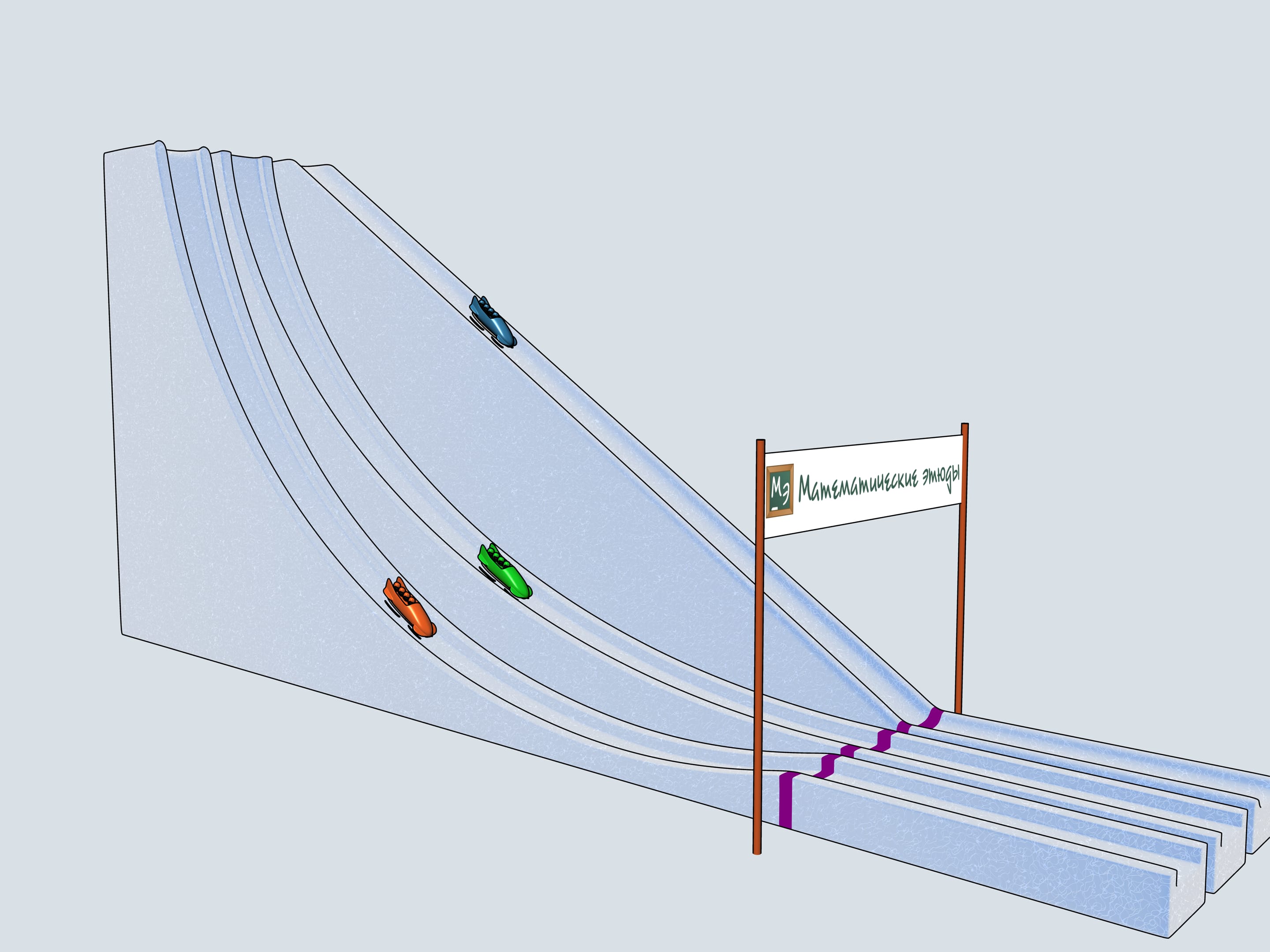
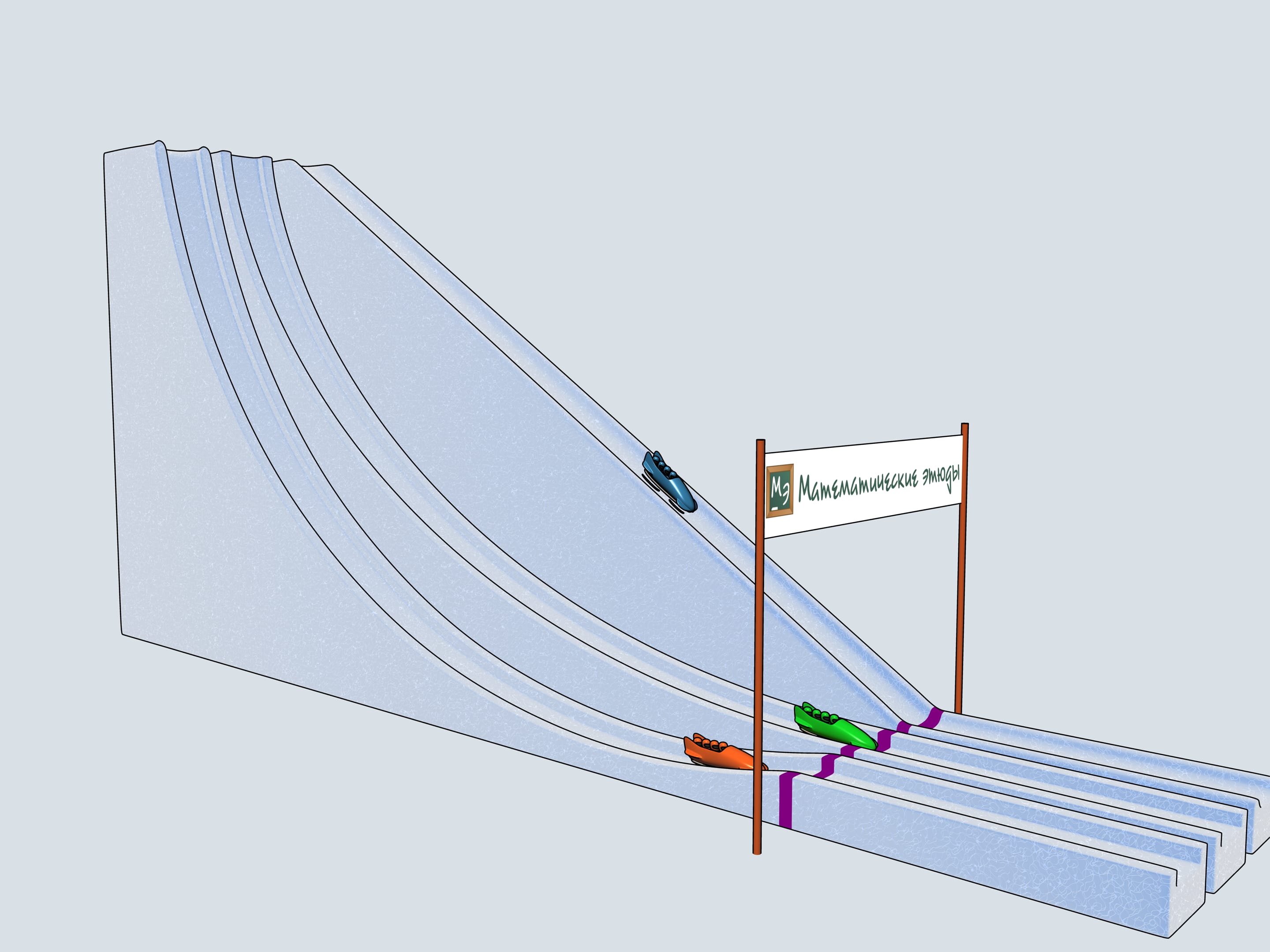
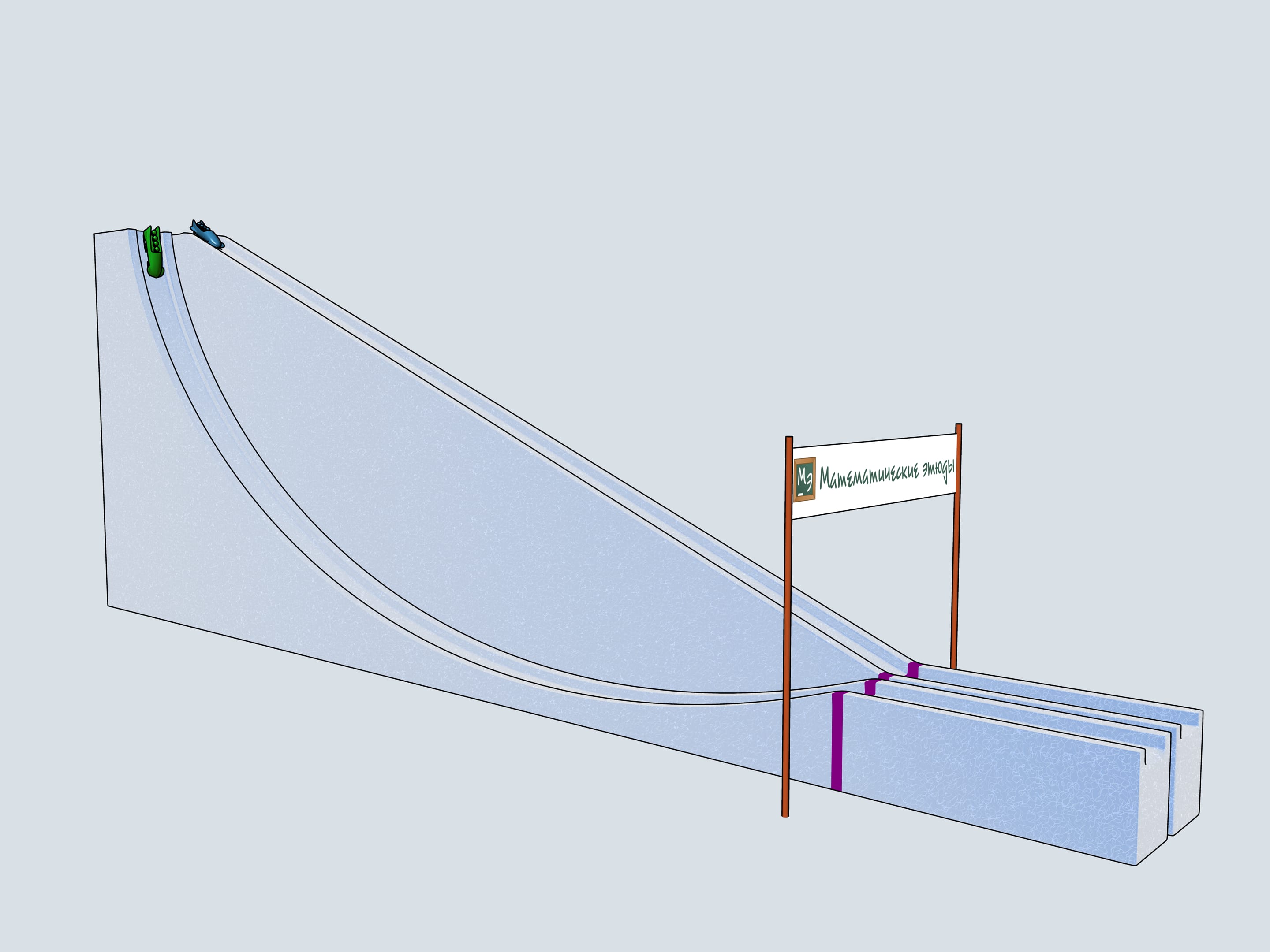
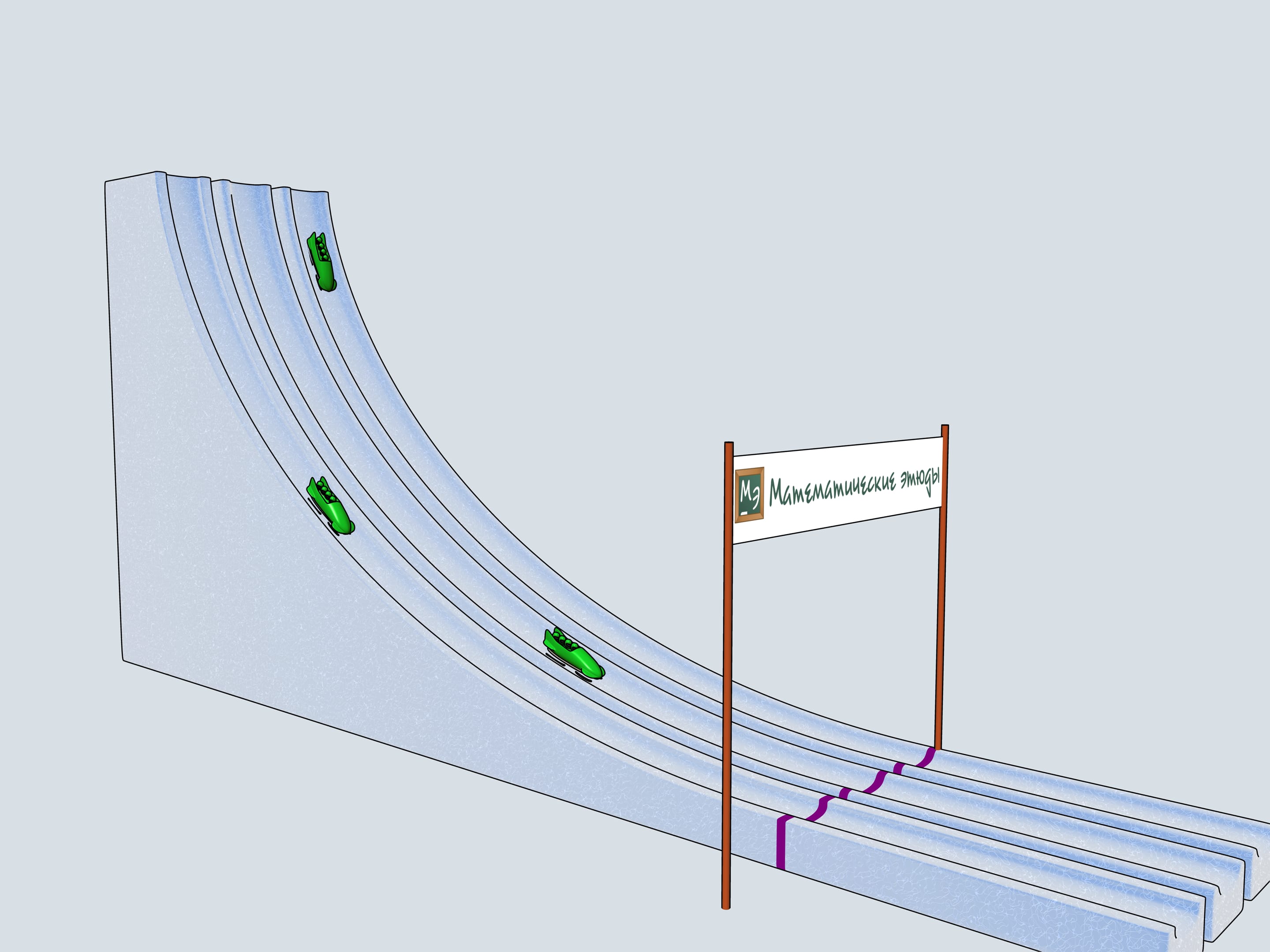
Build bobsleighing tracks of this shapes and watch which of the bobsleigh comes the first.
The history of bobsleighing rises to Switzerland. In 1924 in a french town Shamonie the First Winter Olympics take place. The have already bobsleighing competitions included for couples and quadruples. The only year when a bobsleighing team consisted of 5 persons was 1928. Since then only teams of two and four men compete. There is a lot of interesting in the bobsleighing rules. Of course, there is a limit on the bobsleigh weight, but there are even limitations on the materials one can use in bobsleigh blades (the front pair of them is connected to the wheel and the back pair is fixed). For example, one can not use radium to make his blades.
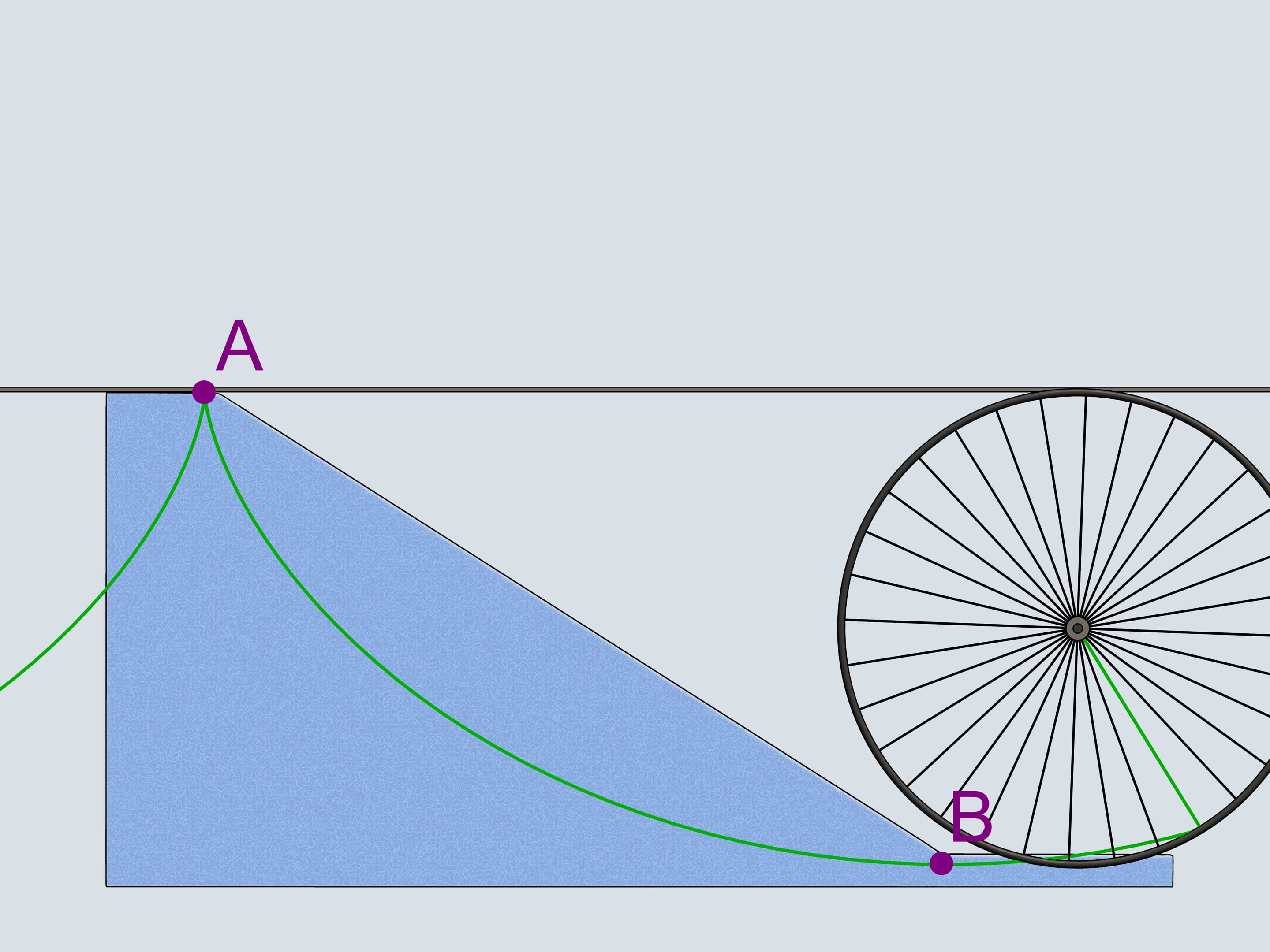
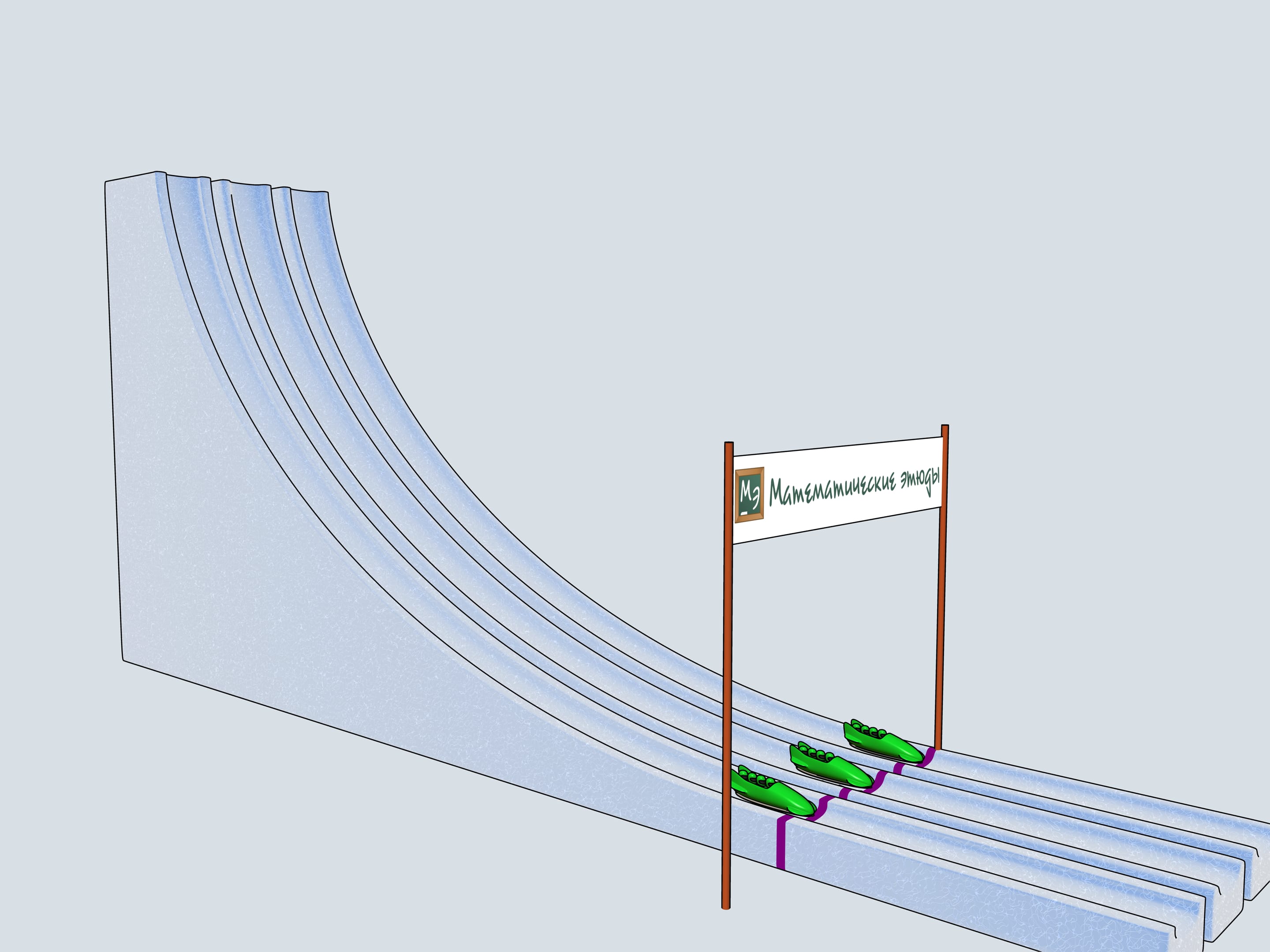
Let's start our quadruples. Which of the bobsleighs comes the first? The green one, sponsored by Mathematical etudes, on the cycloidal track wins!
Why Galileo Galilei considered a quarter of a circle as the best trajectory in the sense of timing? He was inscribing polylines in it and mentioned that increasing the number of edges decreases the time of descent. This is how Galilei naturally came to a circle but made a wrong conclusion that this trajectory is the best among all the others. As we've seen, the best one is a cycloid.
One can draw a single cycloid passing through two give points such that the upper of them is a cuspidal point of the cycloid. Even when the cycloid has to grow up in order to pass through the second point, it remains the curve of the shortest descent!
Another beautiful problem connected to the cycloid is the problem of tautochrone. In Greek tauto means equal, and as we already know, chronos means time.
Build three similar cycloid-shaped slides so that the end of the slide is the peak of the cycloid. Put three bobsleighs on different heights and let them go. An amazing fact is that all of them will finish simultaneously!
In winter you can build a slide of ice and check this property yourself!
The problem of tautochrone is to find such a curve that the time of descent doesn't depend on the starting point.
Christian Huygens proved that the cycloid is the only tautochrone curve.
Of course, Huygens wasn't interested in sliding. At his times scientists couldn't work just for the fun of it. The problems they studied were rising from the demands of engineering. In the XVII century one does long sea voyages. Amazingly, sailors could already determine latitude quite accurately, but couldn't determine their longitude at all. One of the proposed methods to determine latitude was based on accurate chronometers.
The first one to think of an accurate pendulum clock was Galileo Galilei. However, at the moment he starts its construction, he is already old, blind, and his last year of life isn't enough to build one. He entrusts this to his son but he also waits till his death and has no time to finish. The next key character is Christian Guygens.
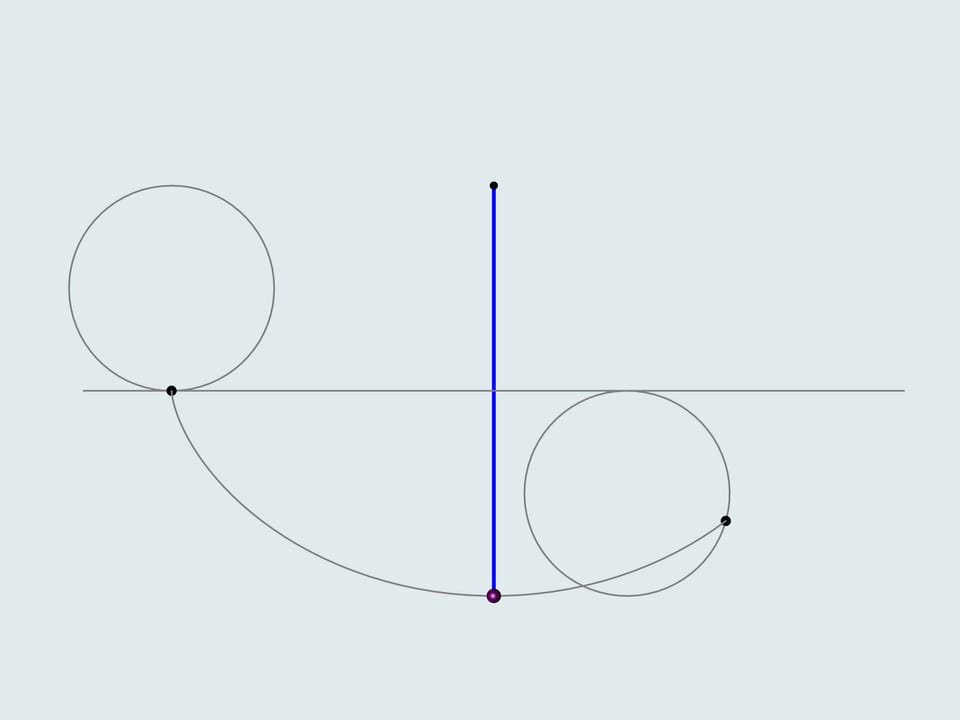
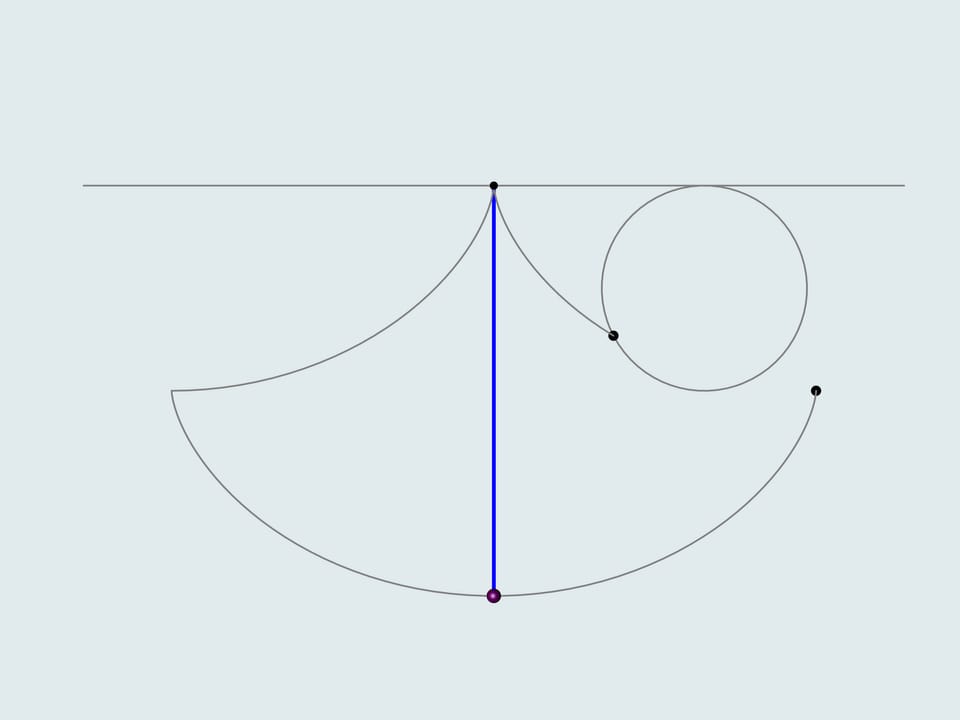
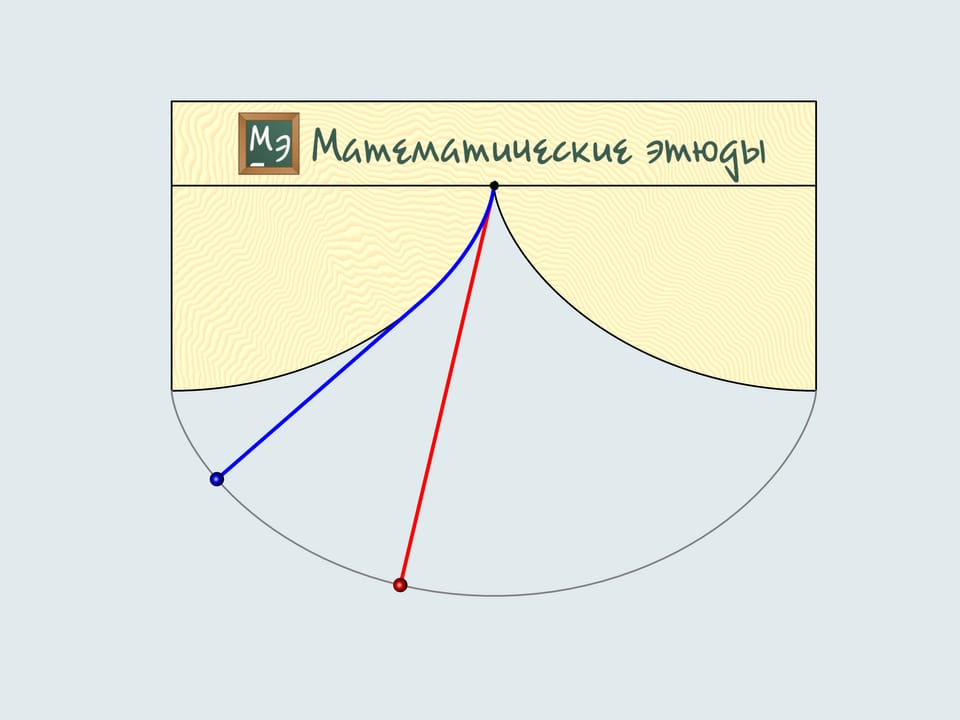
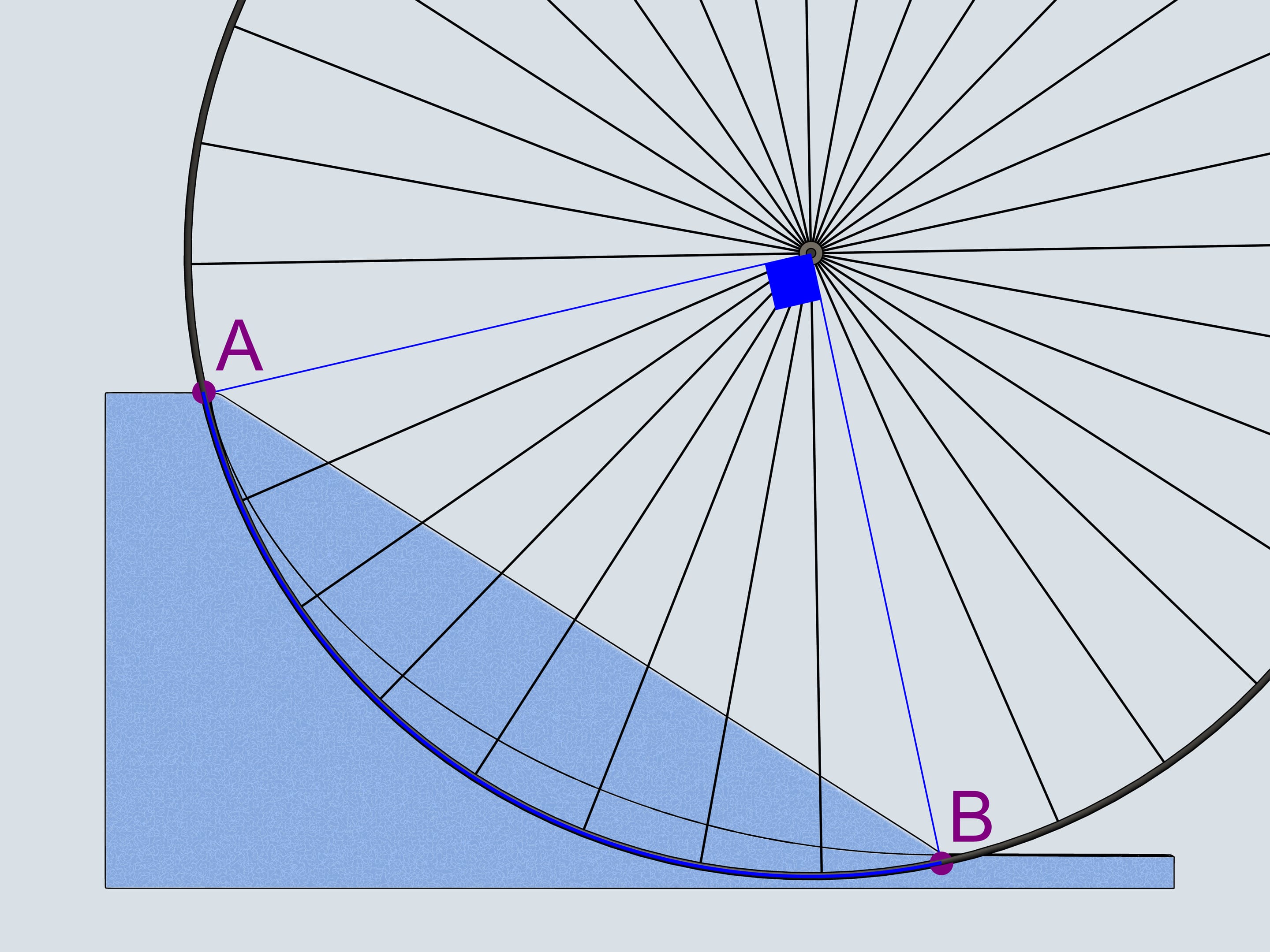
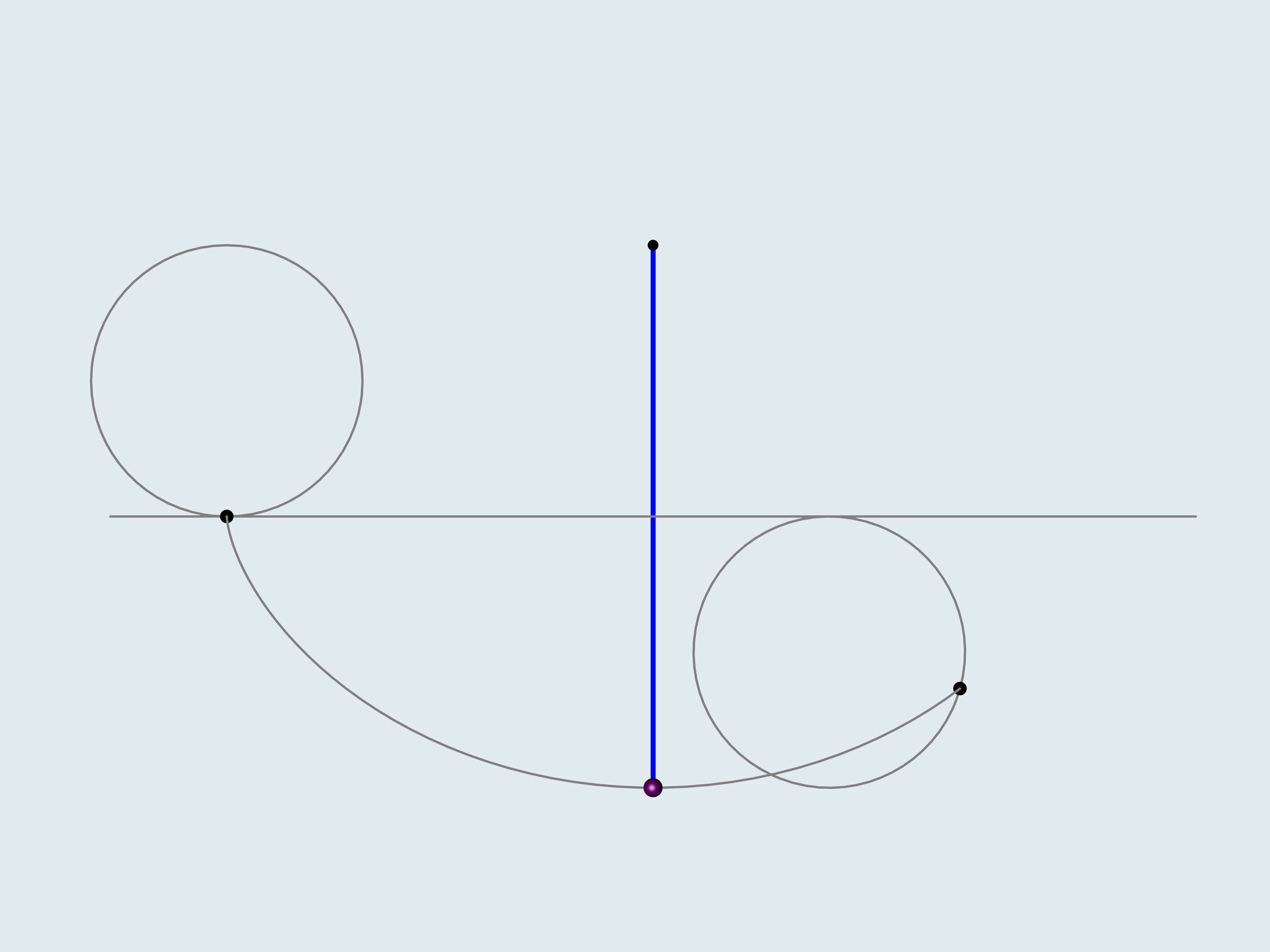
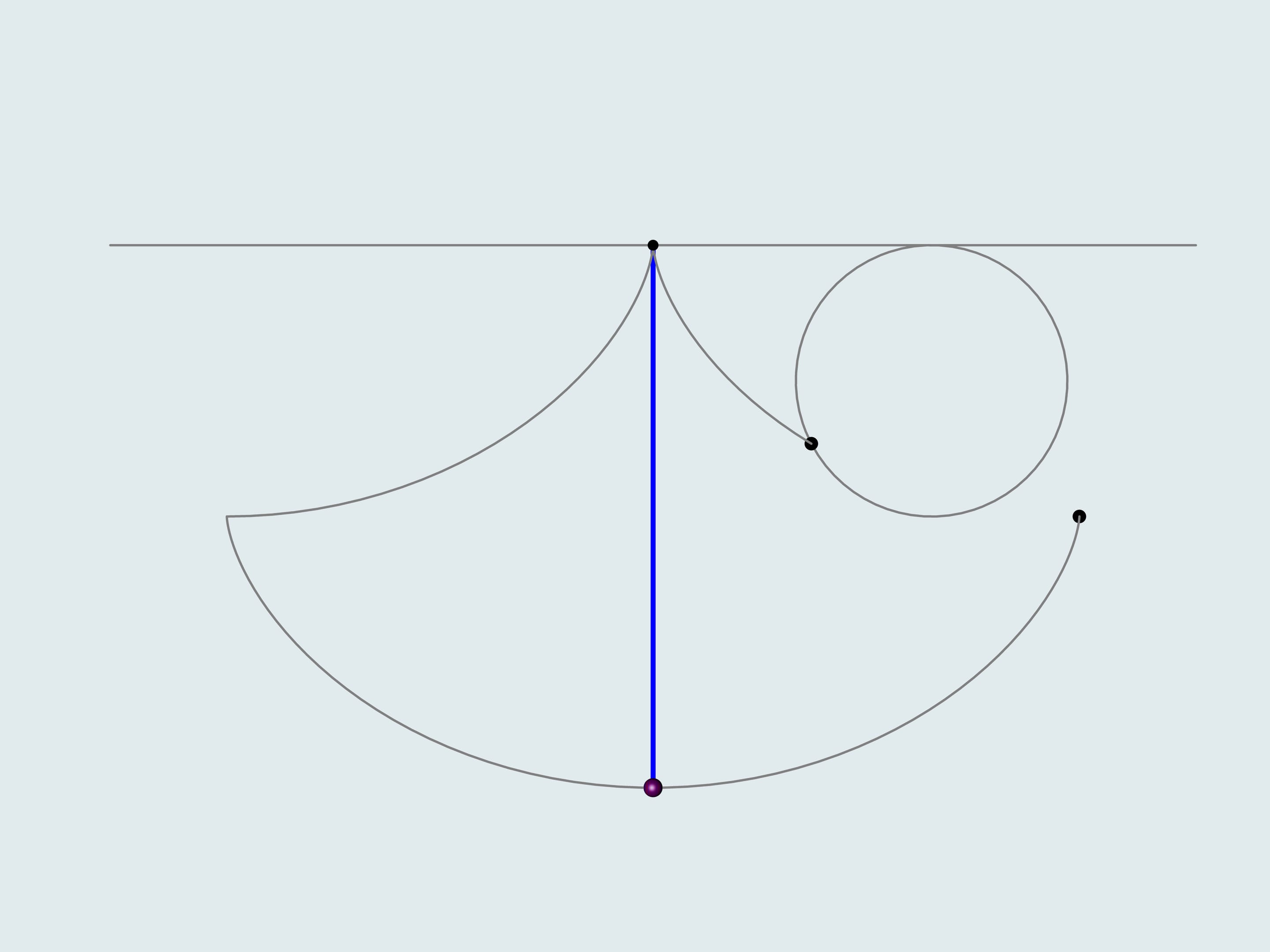
He noticed that the period of swing of an ordinary pendulum, considered by Galilei, depends on the starting point, i.e. the amplitude. Thinking of what the trajectory of the lead weight should be, so that the period doesn't depend on the amplitude, he solver the tautochrone curve problem. But how to make the weight move along a cycloid? Translating theory into practice, Guygens makes cheeks the sting winds on and solves a number of mathematical problems. He proves that the «cheeks» should also have a shape of cycloid showing that the evolute of a cycloid is a cycloid with the same parameters.
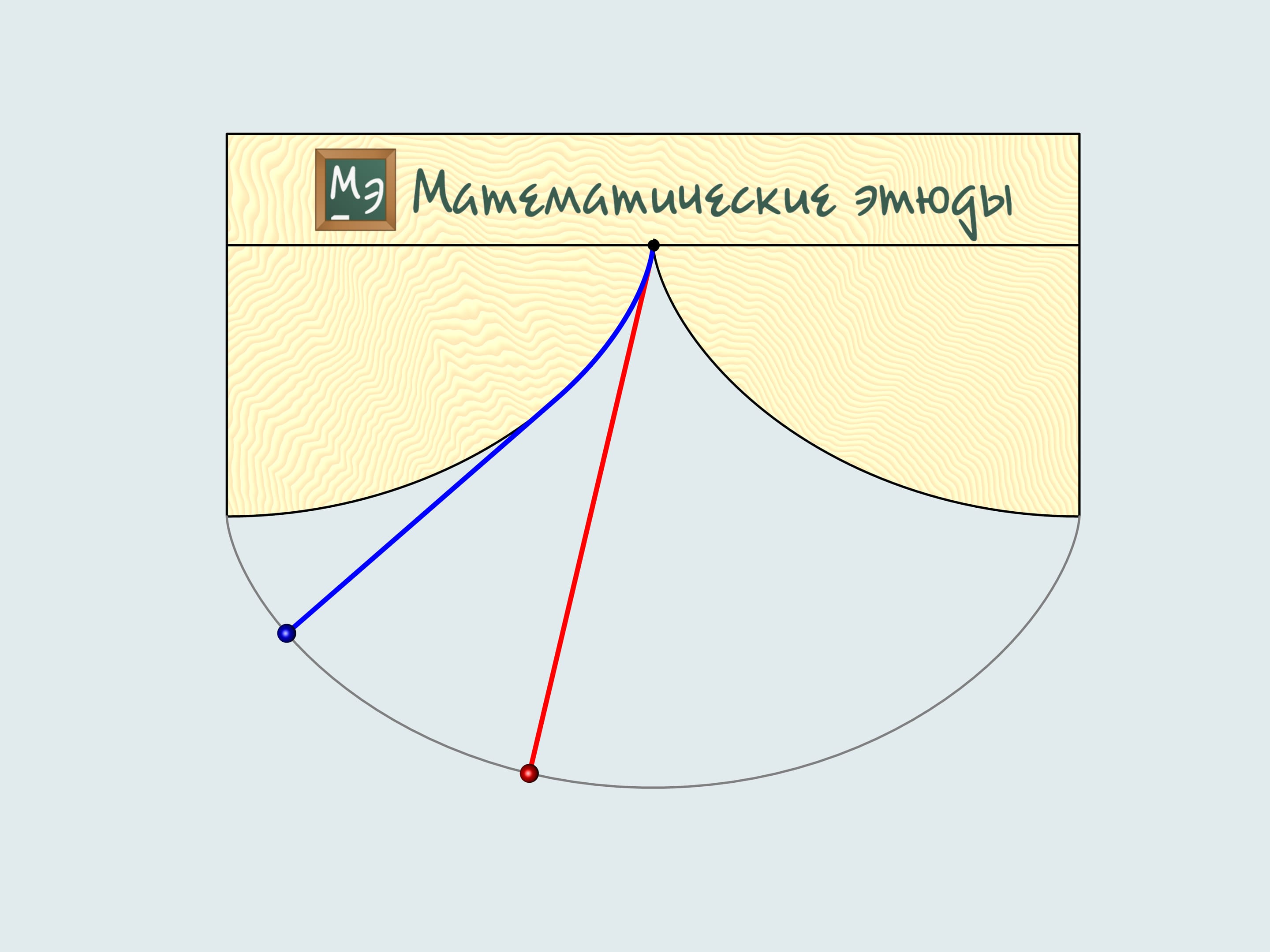
Additionally, the construction of a cycloidal pendulum proposed by Guygens helps to determine its length. If one deflects the blue string, whose length equals four times the radius of the generating circle, it's end will be in the point of intersection of the cheek cycloid and the trajectory, i.e. in the peak of the cheek cycloid. As it's a half of the cycloid's arc, the total length equals eight times the radius of the generating circle.
Christian Guygens constructed a pendulum and the such a clock was tested in sea voyages, but didn't become widespread. As well as the clock with an ordinary pendulum, by the way.
Why do we still have clockworks with an ordinary pendulum? If one looks hard, for small declinations the cheeks almost do not affect the string. Thus, the motions along a cycloid and a circle almost coincide for small declinations.