If you had to construct a wardrobe at home, you remember that while the back is not nailed, it back is put in place, a wardrobe which is a non-closed polyhedron with boundary becomes rigid. If you add the front or add another detail, closing the polyhedron, it will for sure remain rigid.
Are there closed flexible polyhedra?
No one could answer this question for a long time. As always happens in science, one should consider an easier case. In the problem of flexible polyhedra one should work in the plane where polyhedra are replaced by polygons.
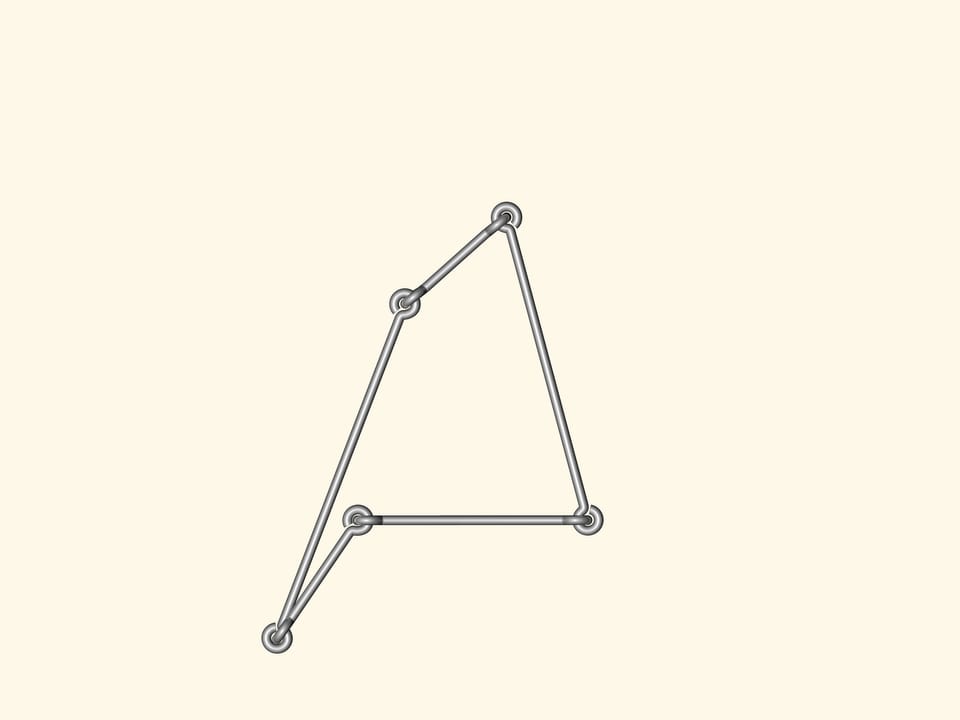
Are there flexible polygons? I.e. such that their sides are fixed, but the angles can change so that the polygon shape changes? Anyone can make such a model from wire using a standard linking in the corners.
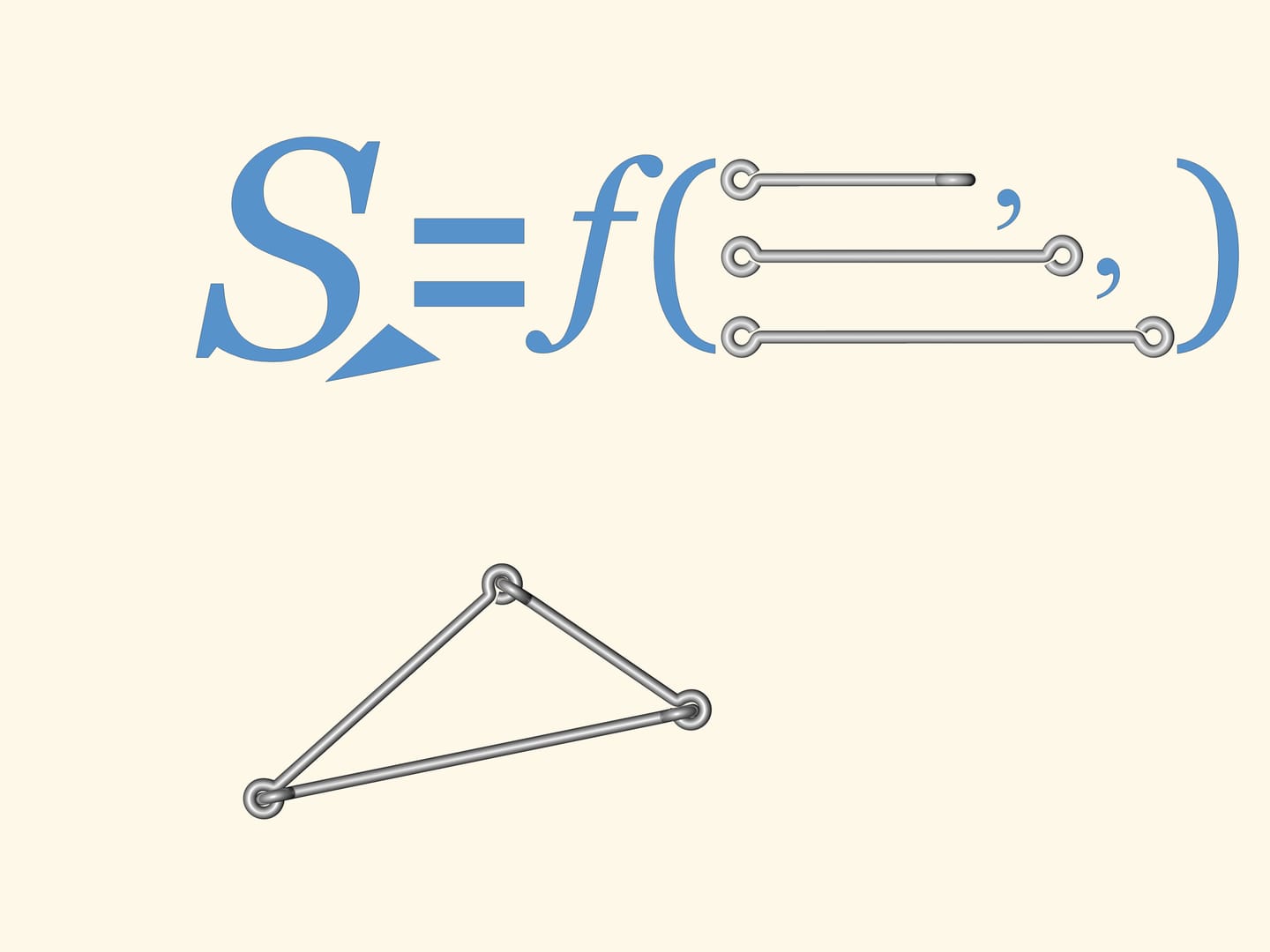
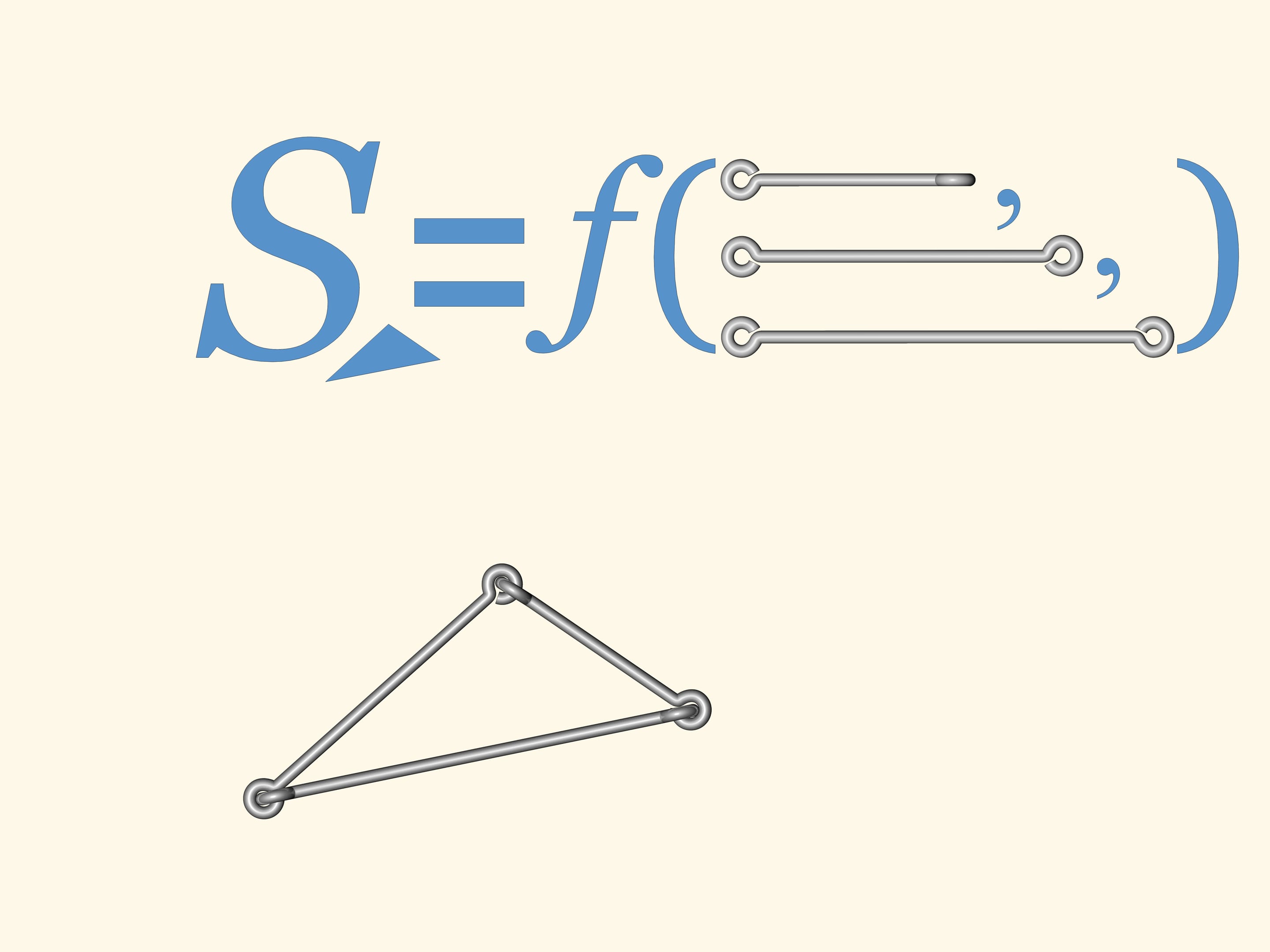
If one makes a triangle, it will not bend. I.e. the lengths of the sides determine completely the triangle. And so, determine its area: the Heron's formula allows to calculate it from the side lengths.
If one makes a wire quadrangle or a pentagon or a polygon with a bigger number of vertices, any of them will bend. As a consequence, there is no Heron's formula, computing the area from the side lengths, for the number of angles greater than three.
Let's return to the space. What is a flexible polyhedron if it exists? Analogically to the flat case, the faces (being of one dimension less than the space) should be rigid plates. And dihedral angles connecting the faces should be able to change, as if the edge (a face of dimension one) was realized as a hinge.
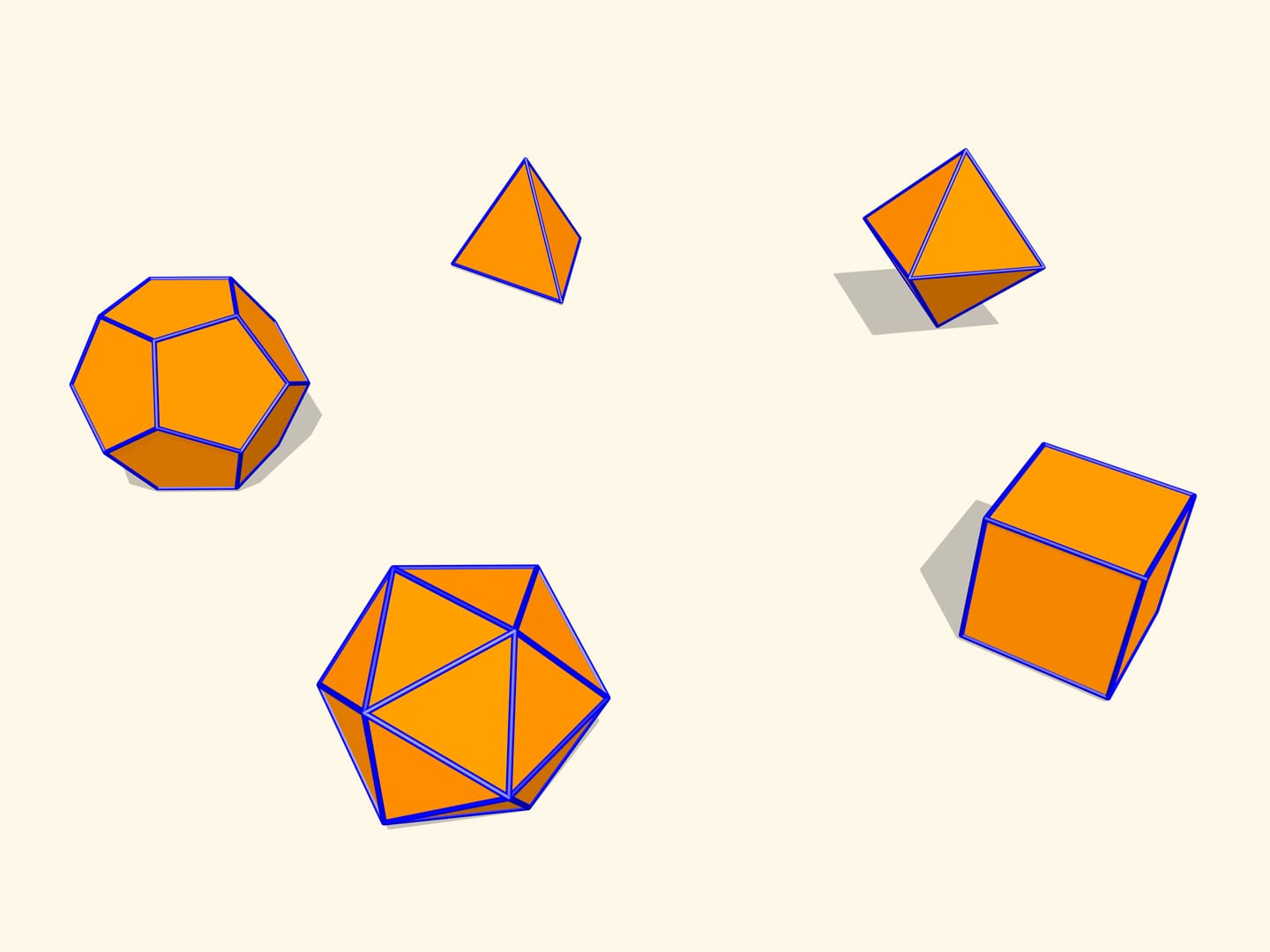
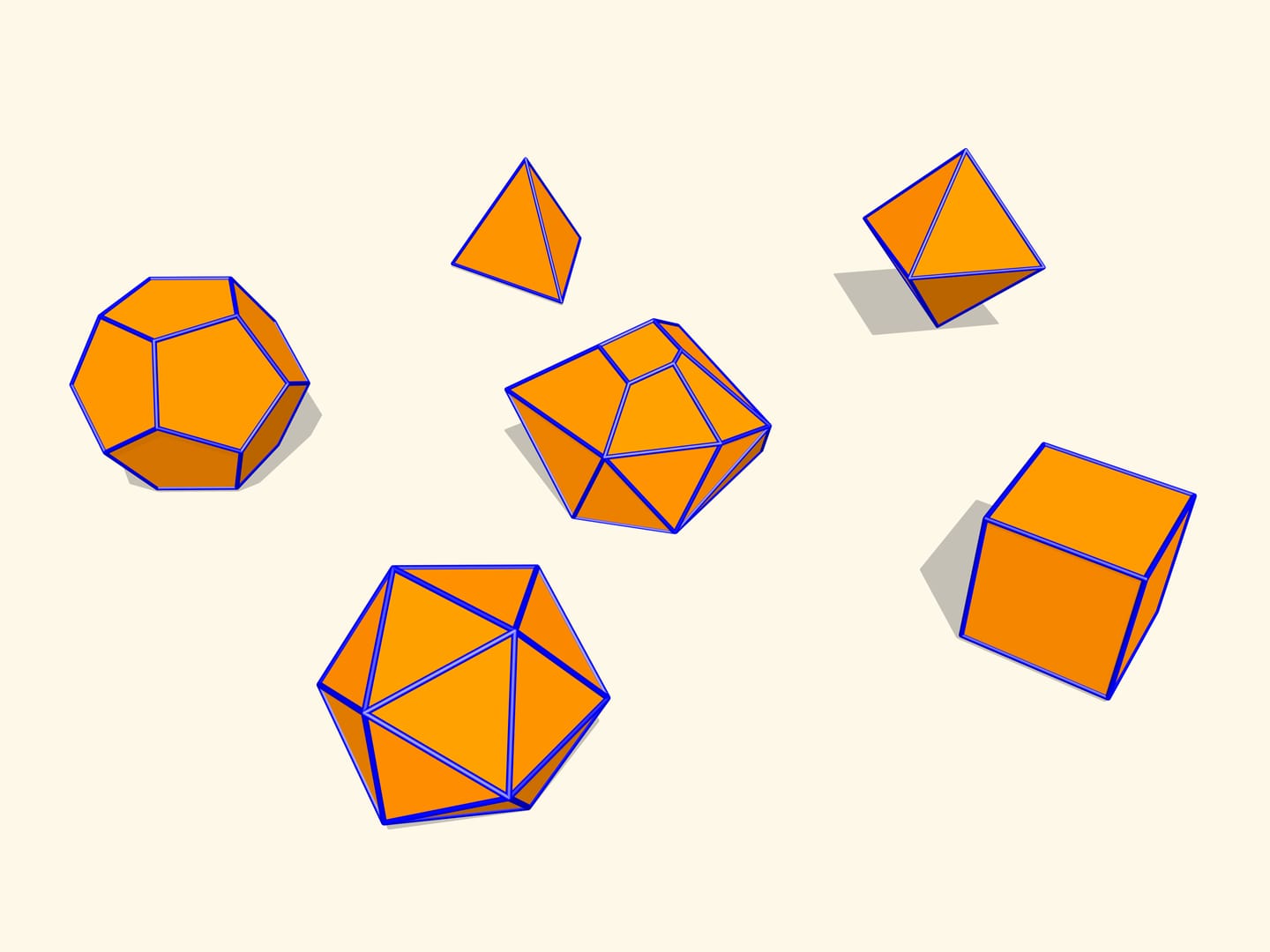
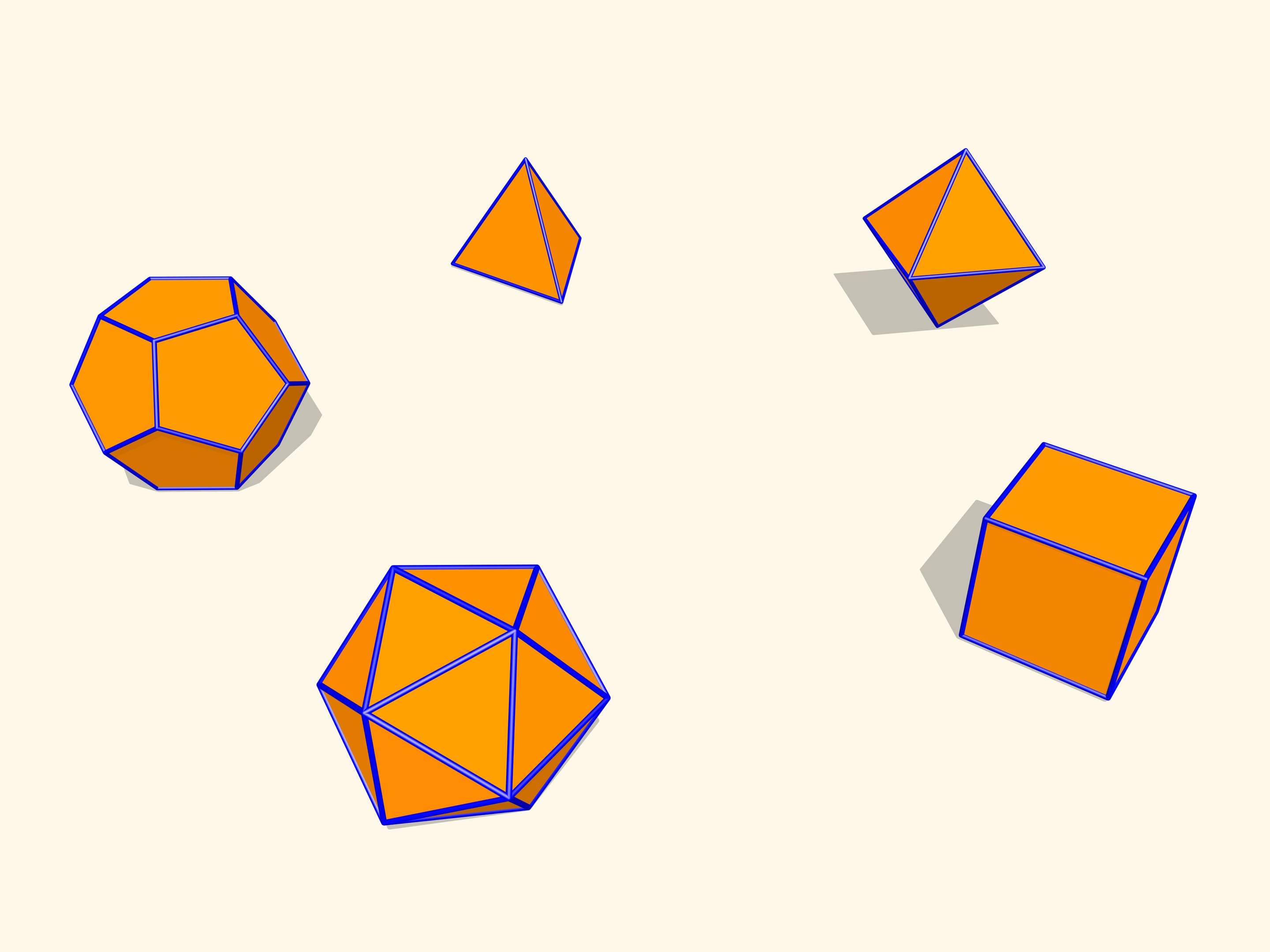
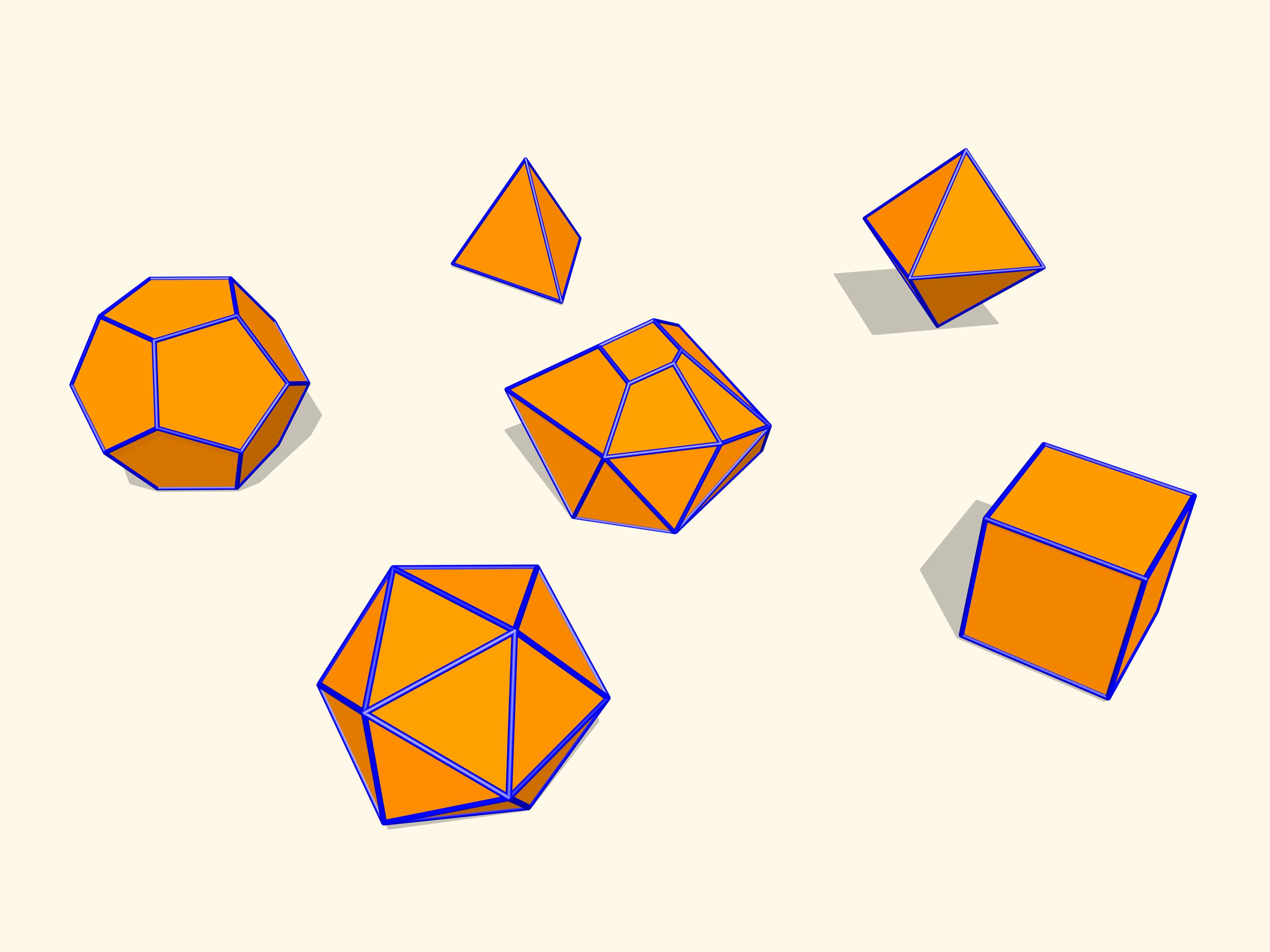
Let's consider regular polyhedra. If one makes their models with hinges as edges, one can check that they will not bend. It turns out that this is a general fact for convex polyhedra. A theorem proved by a french mathematician Augustin-Louis Cauchy (1789 – 1857) in 1813 states that a convex polyhedron with a given set of faces and gluing conditions is unique. I.e. a convex polyhedron can not be flexible.
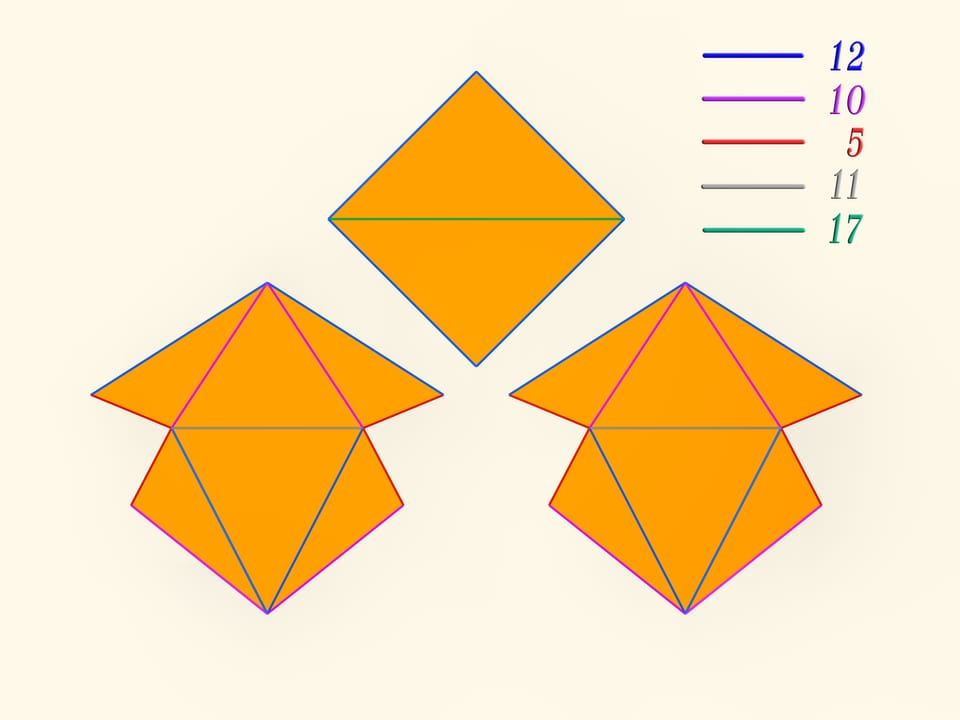
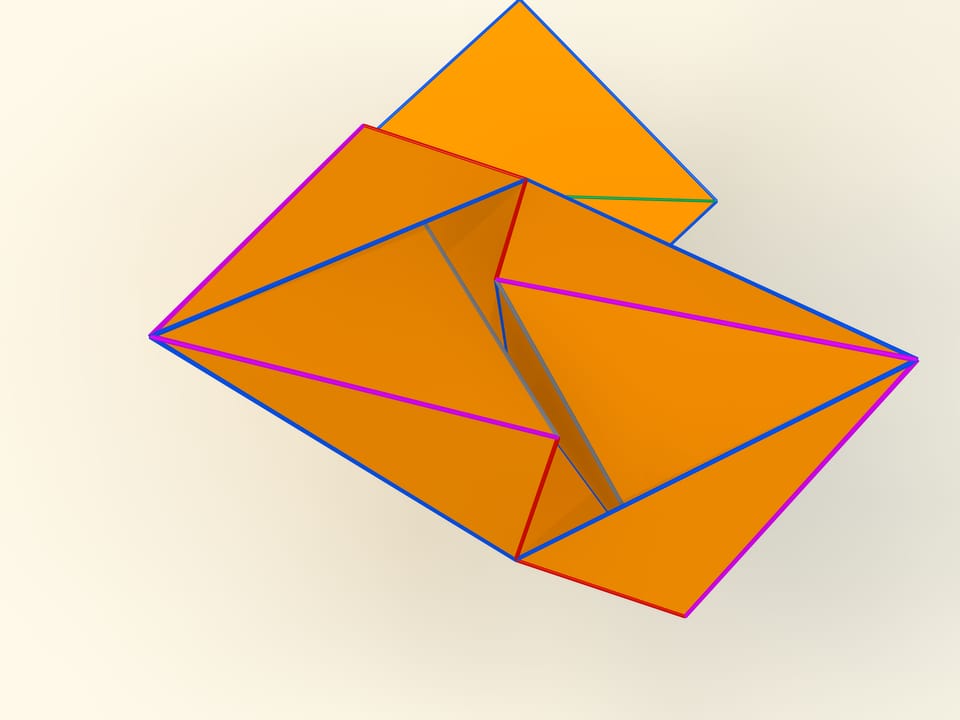
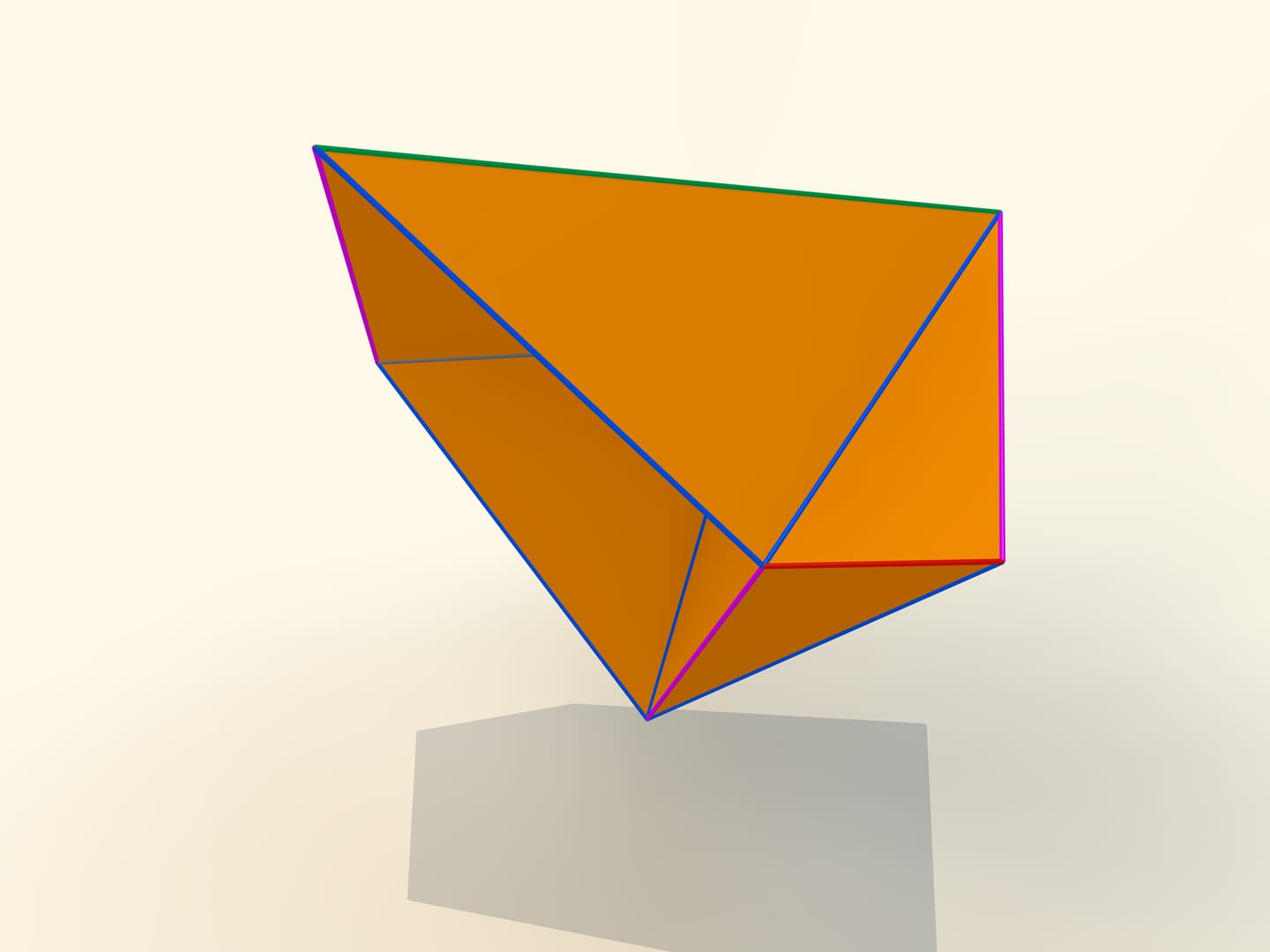
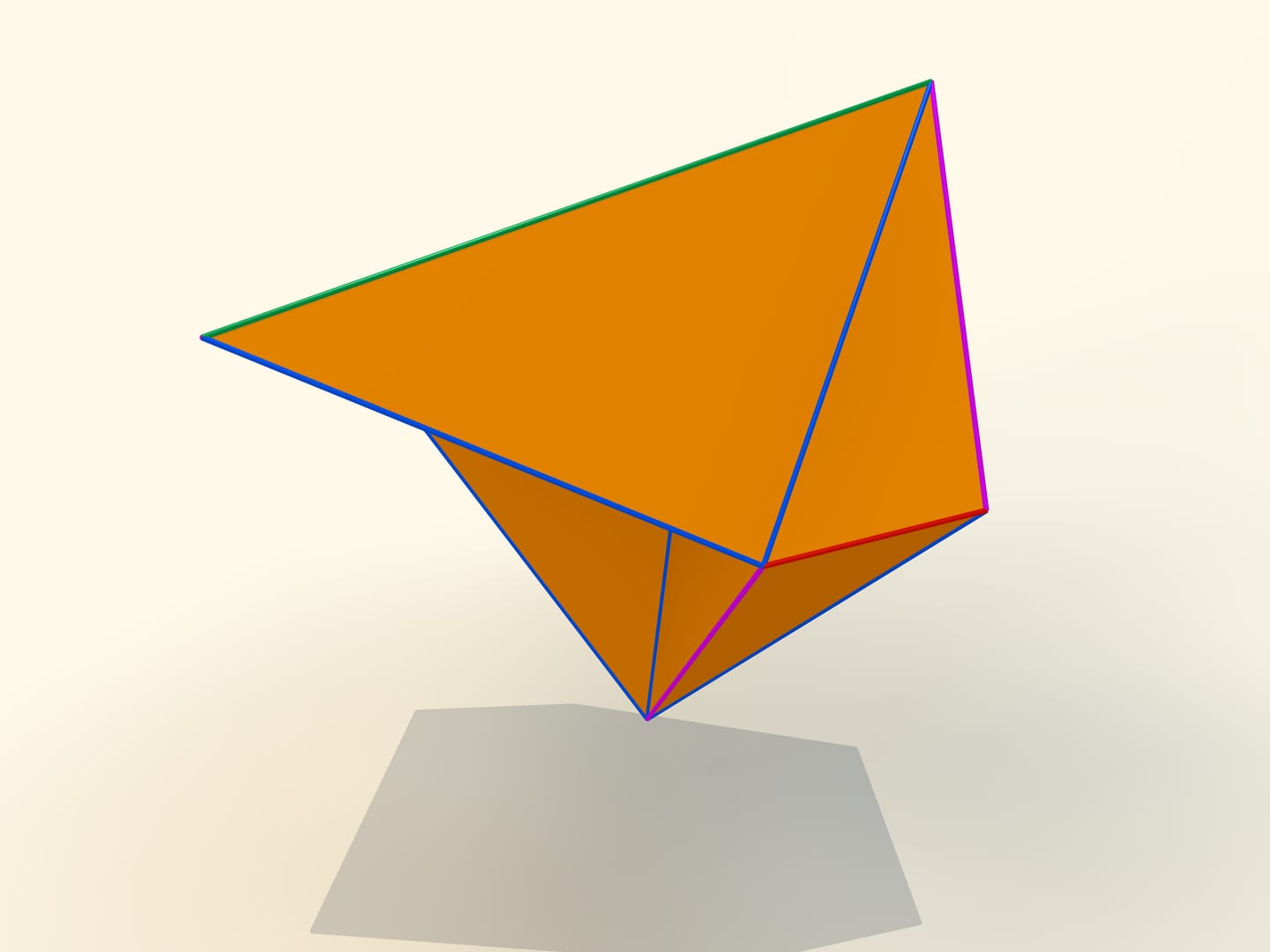
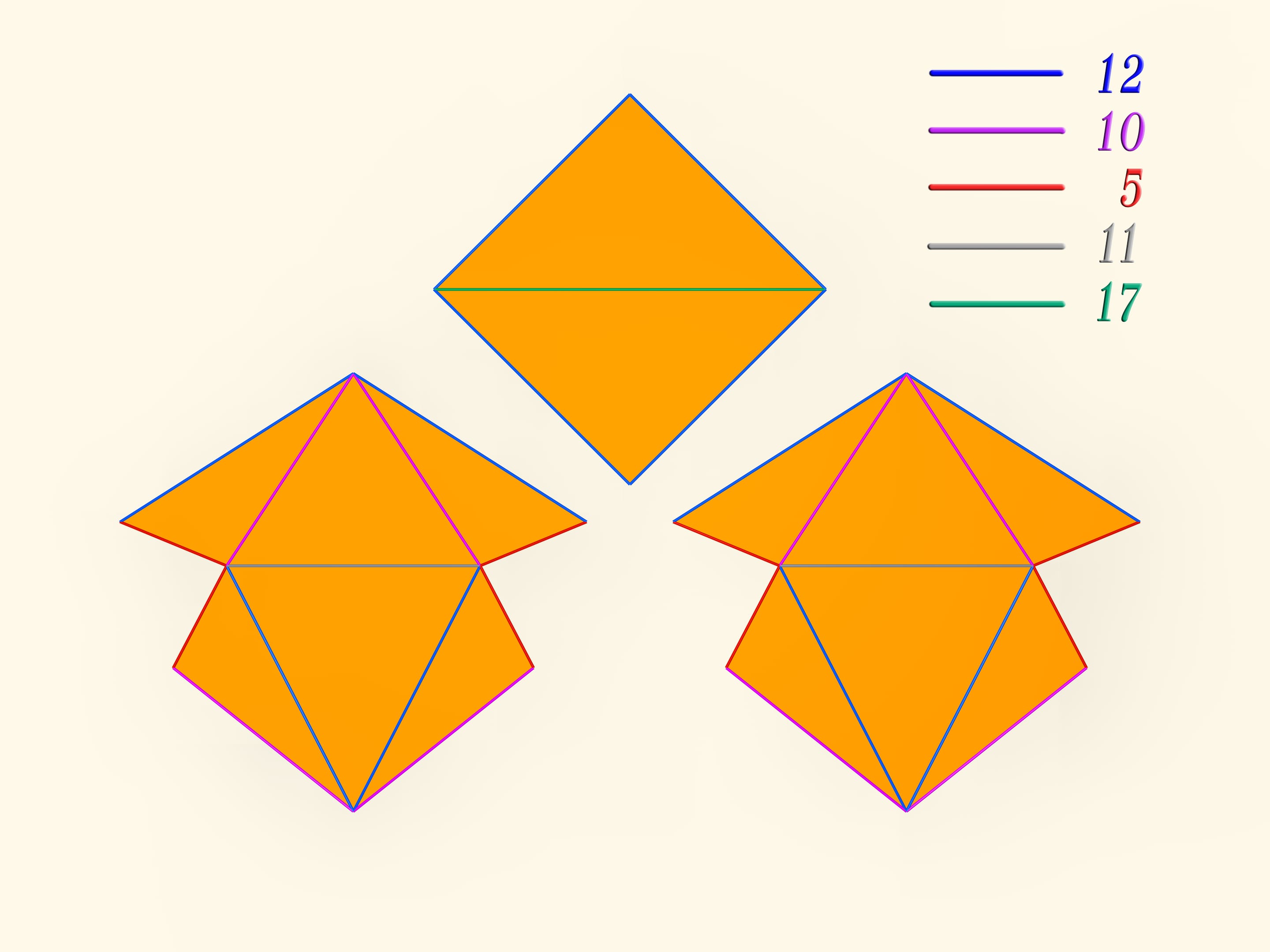
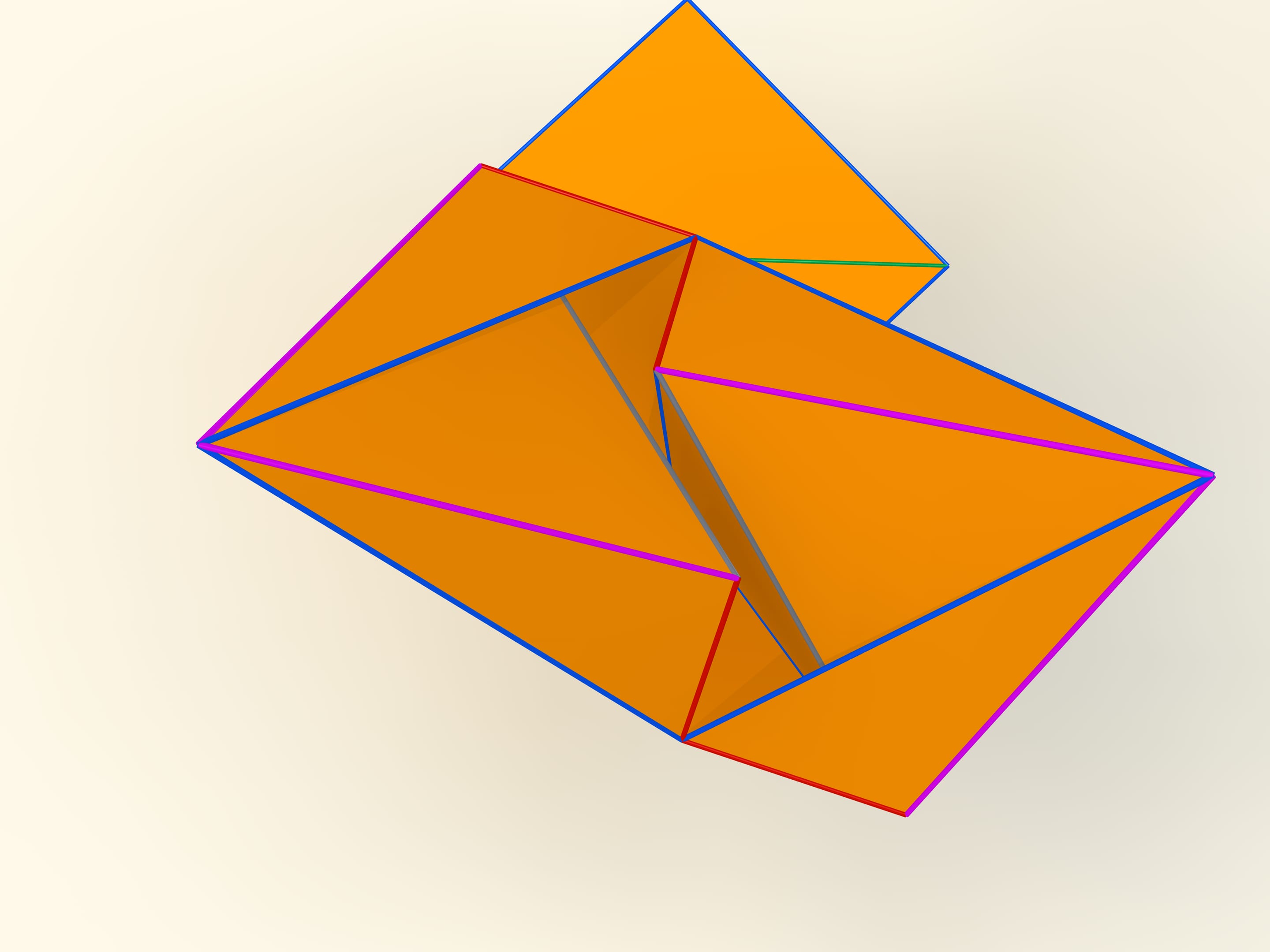
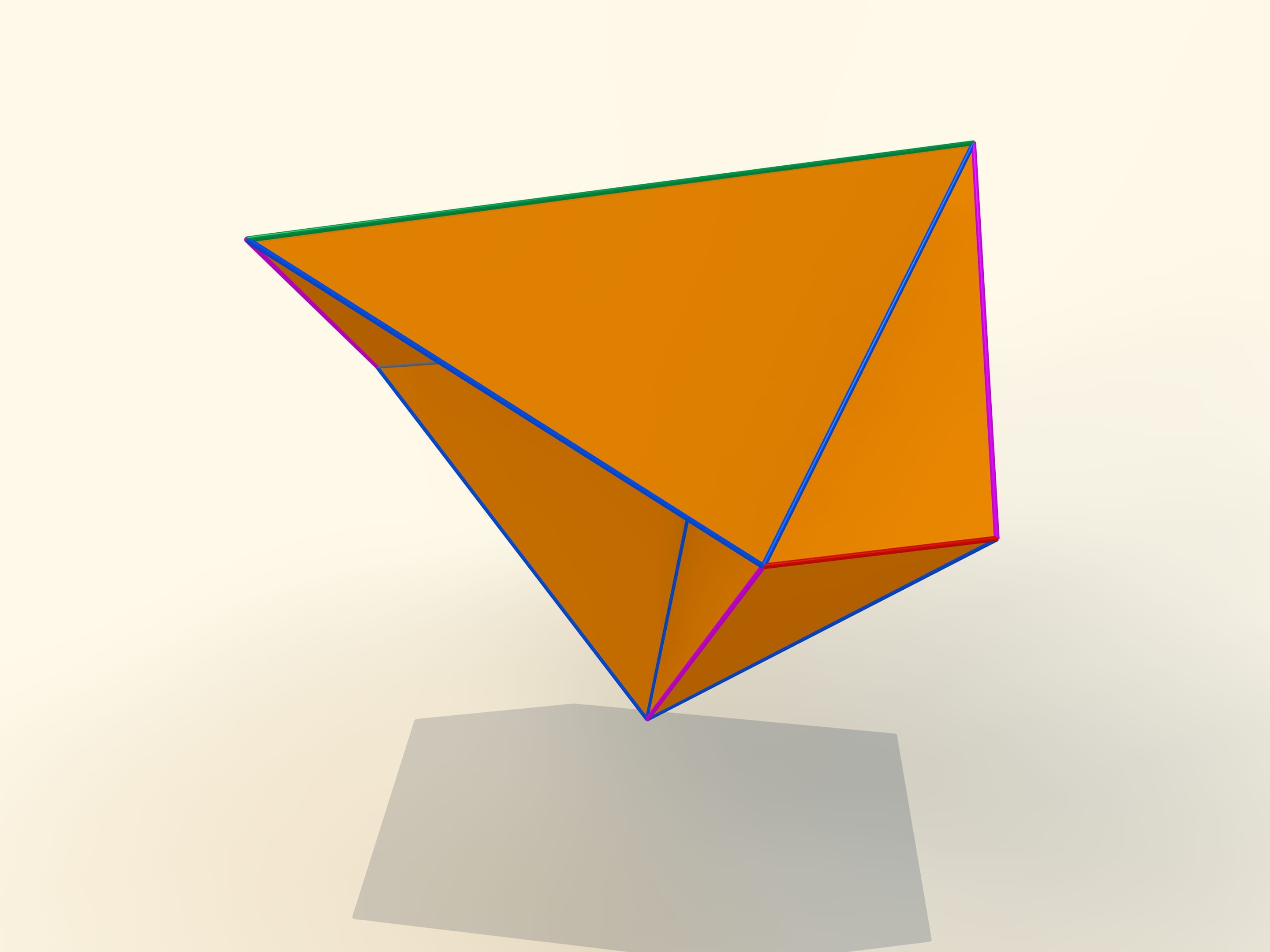
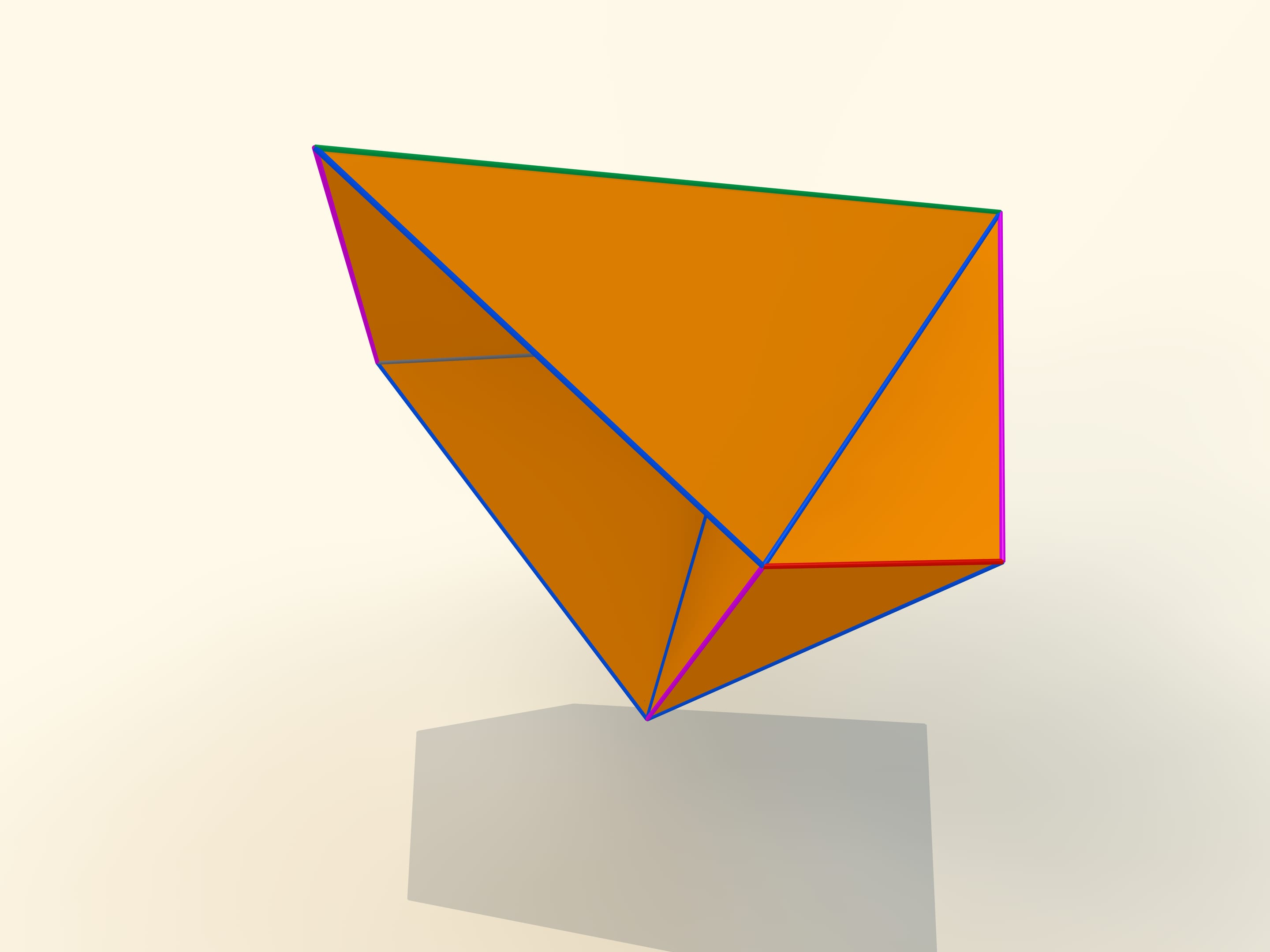
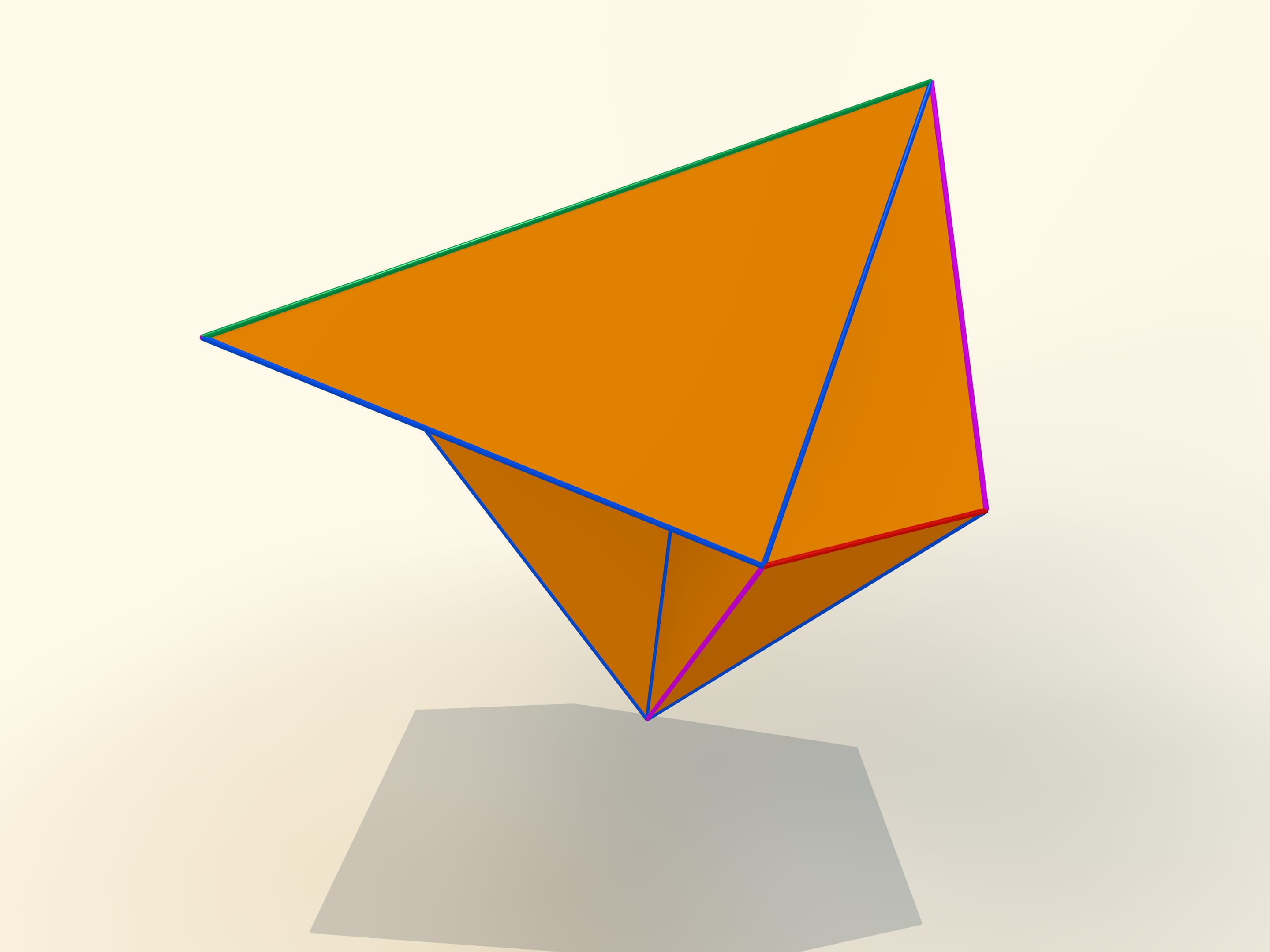
The first mathematical examples of bendable polyhedra, of course, non-convex, as well as the classification of such objects, were constructed by a belgian engineer R. Bricard in 1897. Mathematical, because these polyhedra were not only non-convex, but also self-intersecting: their faces intersected each other. For the point of view of a mathematician, this is also a polyhedron that can not be realized in our three-dimensional space. In 1975 an american mathematician R. Connelly found a way to get rid of self-intersections and the first real flexible polyhedra appeared. The simplest known today, consisting of 9 vertices, 17 edges and 14 faces, will be now constructed. It was invented in 1978 by a german mathematician Claus Steffen.
A net of the Steffen polyhedron consists of two similar parts and a «cover». If you remember the shape of the net, but not the lengths of the edges, it's hard to build such a polyhedron yourself: an ability to bend is exceptional for polyhedra and there is not a lot of them.
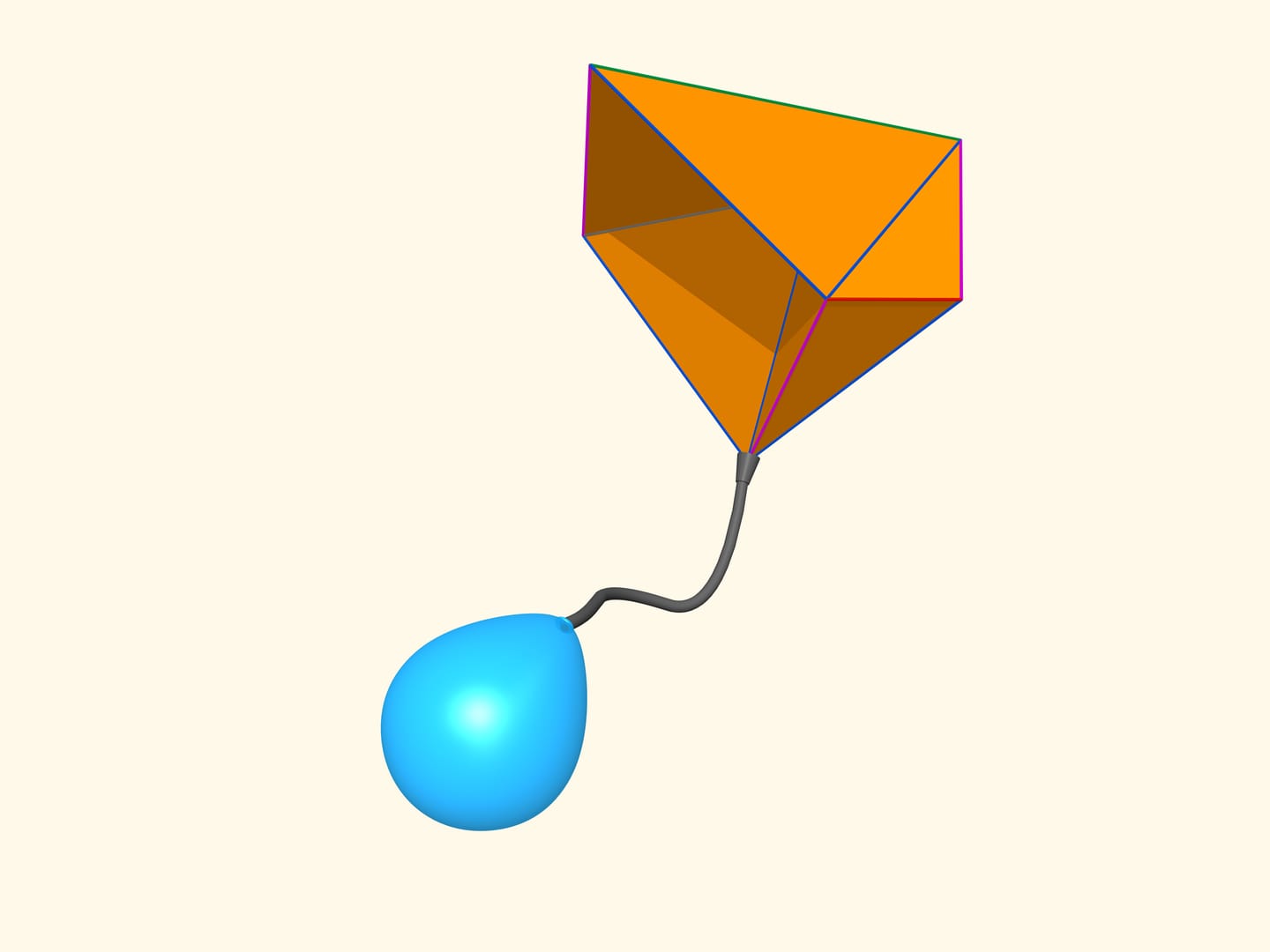
When mathematicians found out that such polyhedra exist, they asked a question which is now called «bellows conjecture». Why do bellows fan the coals? Why does the internal volume change. And what about flexible polyhedra: will their volume change while bending? Can one build an accordion or bellows out of rigid plates and not of leather?
In the end of the XX century the question was fully answered by a russian mathematician I.H. Sabitov. It turns out that there is a Heron type formula for the volume of polyhedra, so for flexible ones. Namely, there exist a polynomial of one variable such that it's coefficients depend only on the edge lengths of the polyhedron and the volume is a root of this polynomial. As edges of flexible polyhedra do not change while bending, the polynomial and its roots do not change either. But different roots of this polynomial are some particular numbers situated at some distance one from another. Small bending should provide small changes of volume, so it can't jump from one root of the polynomial into another. Thus, the volume of flexible polyhedra doesn't change while bending!
We considered both the cases of flexible polyhedra in the plane and in the space. But what happens in greater dimensions? There are also some flexible polyhedra, but much less. And the question about the constancy of volume of flexible polyhedra in higher dimensions is still open and waiting for its researcher.