A picture you know from childhood. Kaleidoscope. Its name comes from the ancient Greek words καλός — beautiful, εἶδος — view, σκοπέω — watch, observe. This optical gadget was invented by a scientist in the early XIX century and has quickly become a popular entertainment in many countries, including Russia.
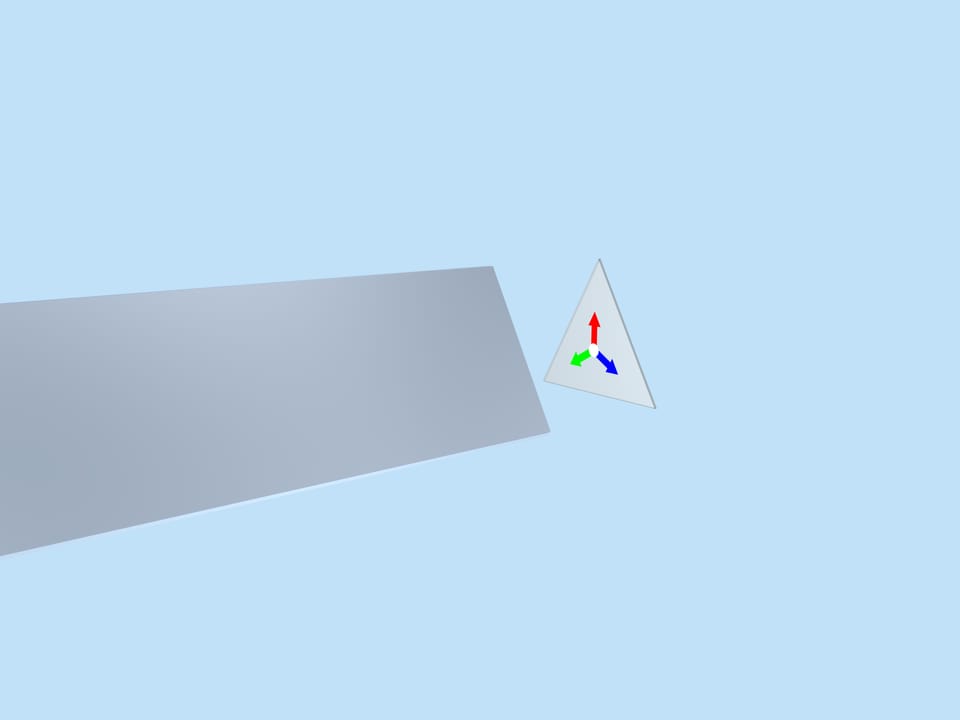
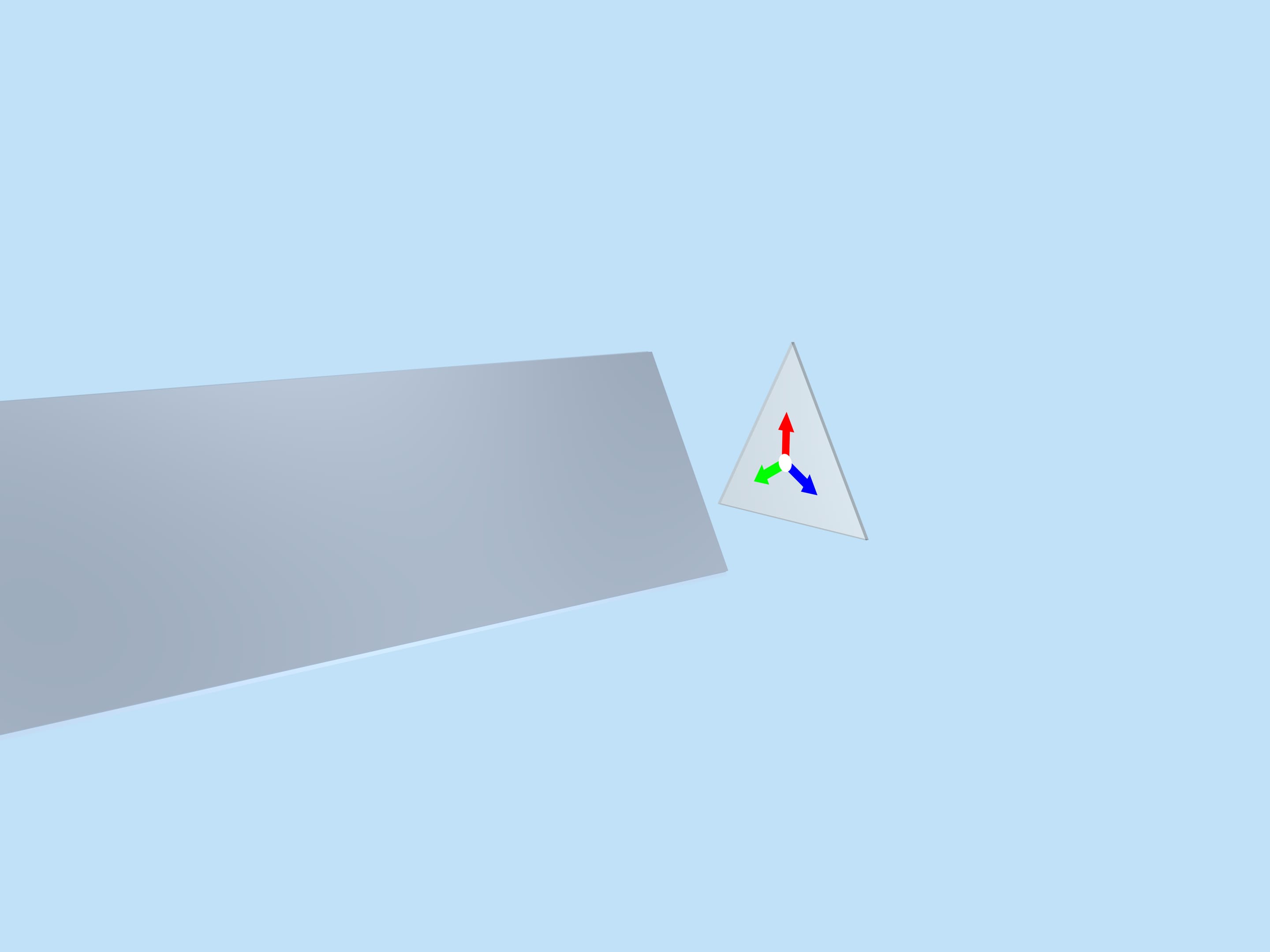
Those who used to take apart a kaleidoscope as a child for the “research purposes” will remember that there are three mirrors in the shape of long rectangles inside cylindrical tube. They form a reflective triangular prism. Behind the triangle at the base of the prism (we will call it the fundamental triangle), there is a container in which, as the kaleidoscope rotates, small coloured objects are shuffled around forming a random image. The image formed in the fundamental triangle is reflected in mirrors and fills the whole image plane in a beautiful way.
The word “beautiful way” means something different for each person, but let’s try to distinguish some mathematical properties in the image formed in the kaleidoscope.
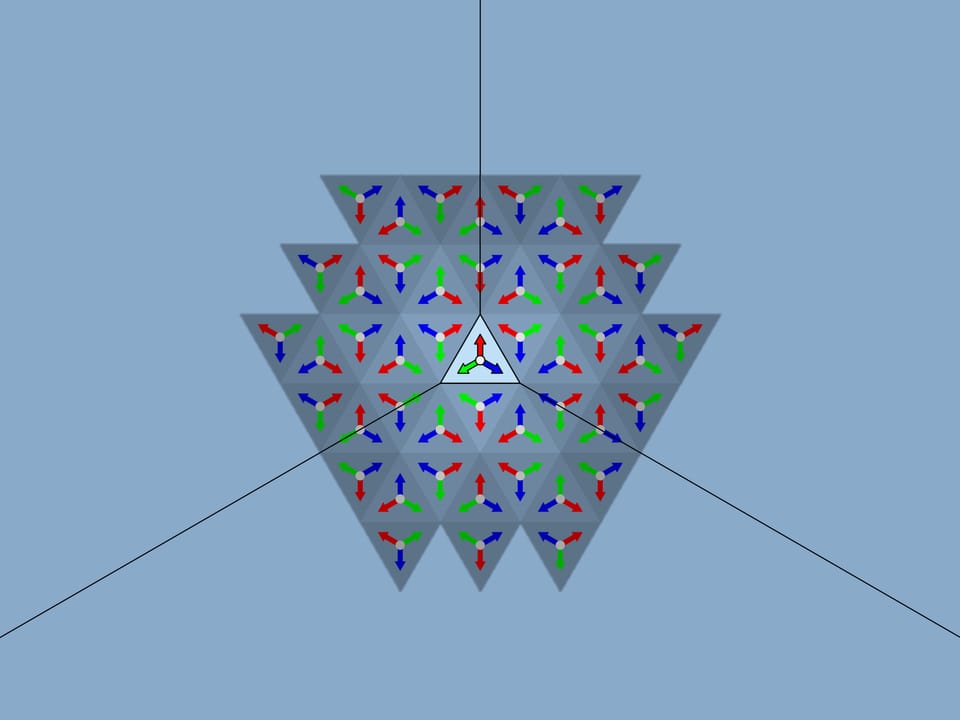
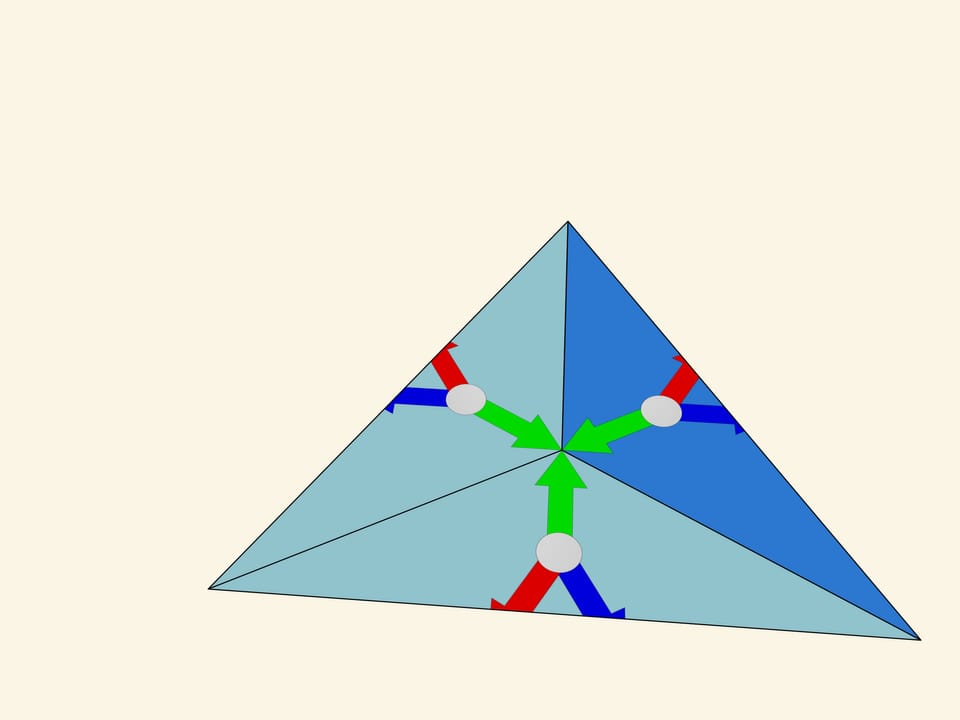
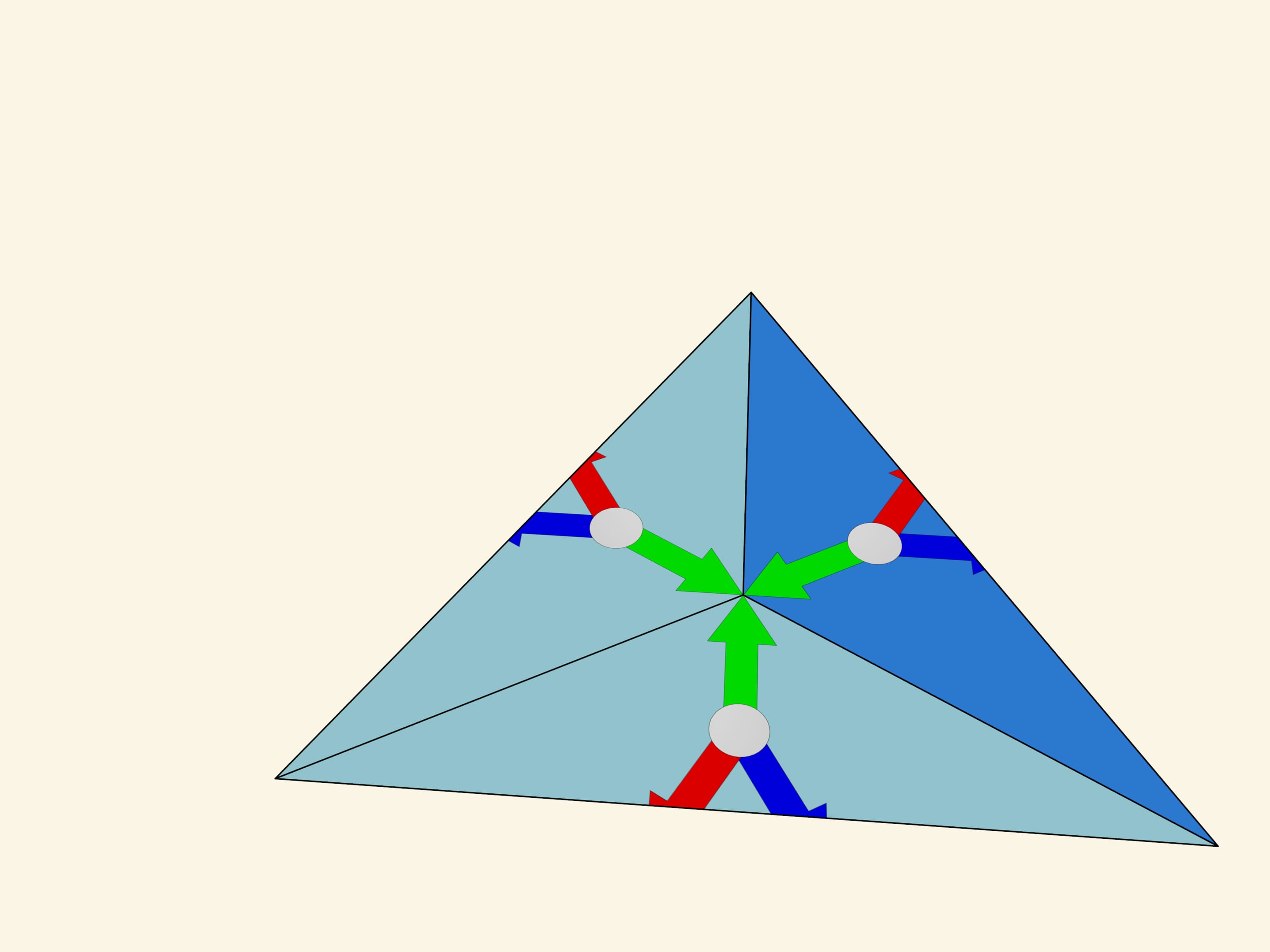
The image formed in the fundamental triangle at a particular moment, of course, affects the beauty of the overall image, but it is random and changes with rotation, and thus our considerations should not depend on it. Let’s replace it with a simpler one, mathematically related to the fundamental triangle itself — three multi-coloured arrows of equal length, laid out from the triangle centre perpendicular to the mirrors.
The “beauty” of the image in the kaleidoscope depends on which fundamental triangle is reflected in the mirrors. The resulting image must fill the whole plane, the different copies-reflections of the fundamental triangle must not overlap each other, creating a mishmash, must not be cropped. And the main property of a “correct” kaleidoscope is that an observer should see the image formed after the reflection in the mirrors as a real object: the image should not change if one moves relatively to the mirrors.
What can be angles of the fundamental triangle (angles between mirrors) so that the properties stated above are fulfilled?
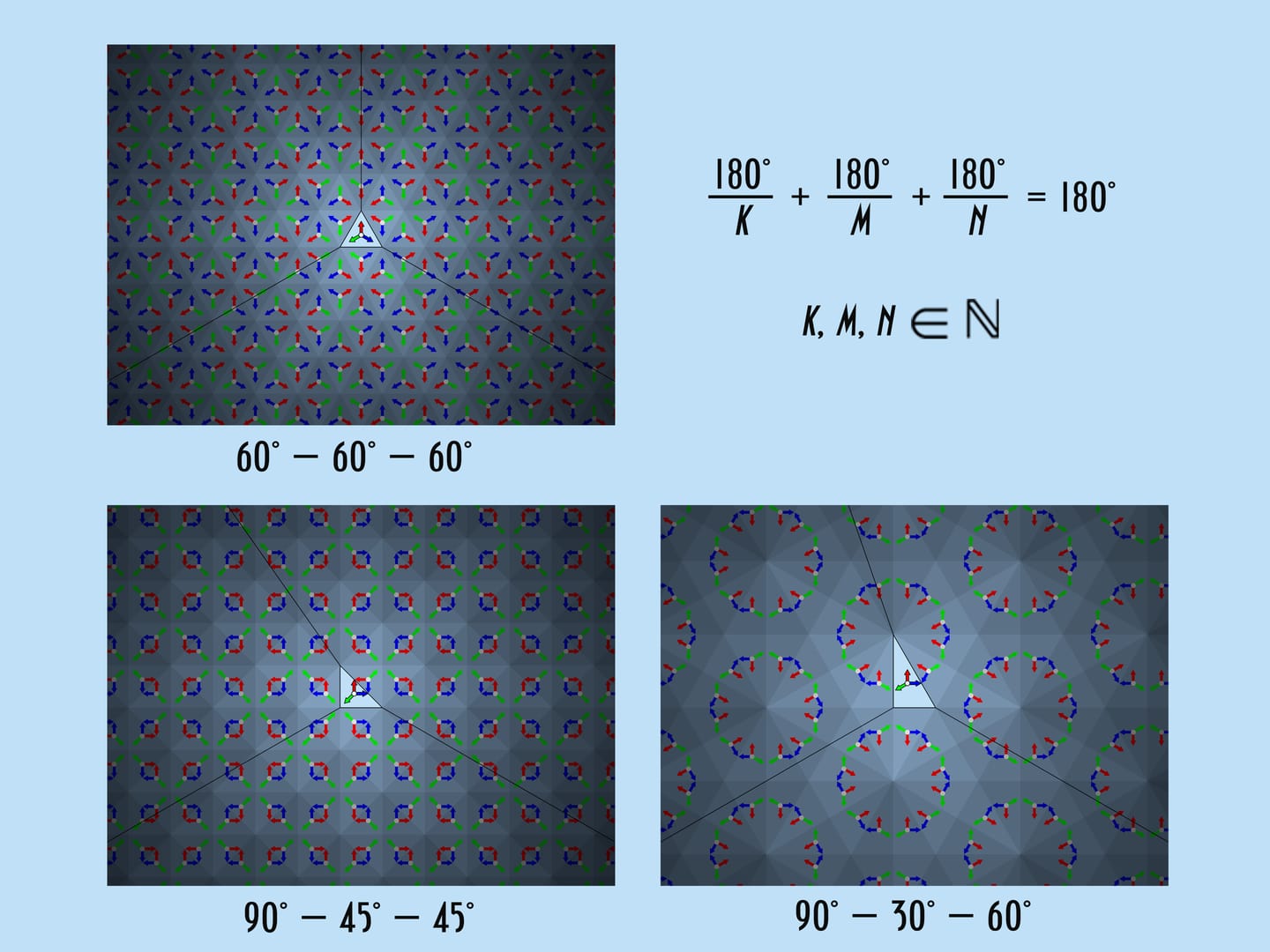
In the most common type of kaleidoscope, the triangle at the base of the prism is equilateral, with angles $60^\circ $—$60^\circ $—$60^\circ$. This is also convenient from a manufacturing point of view — all mirrors are the same. Are any other sets of angles possible?
Let’s try to make a mirror prism with a base as an arbitrary triangle. After reflections, the observer will see a lot of debris of the image formed in the fundamental triangle and the whole image won’t be nice. So a beautiful image is a big success.
Besides the equilateral triangle with angles $60^\circ $—$60^\circ $—$60^\circ$ there are only two other triangles that give a beautiful image. They are right triangles with angles $90^\circ $—$45^\circ $—$45^\circ$ and $90^\circ $—$30^\circ $—$60^\circ$. To verify this, let’s mathematically build the image appearing in the kaleidoscope.
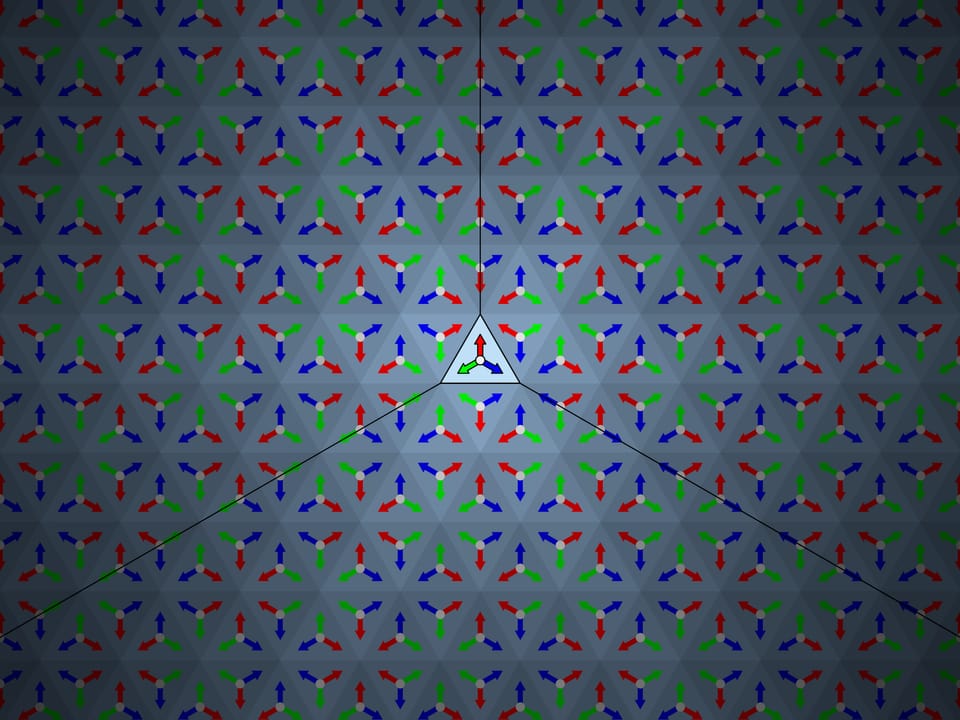
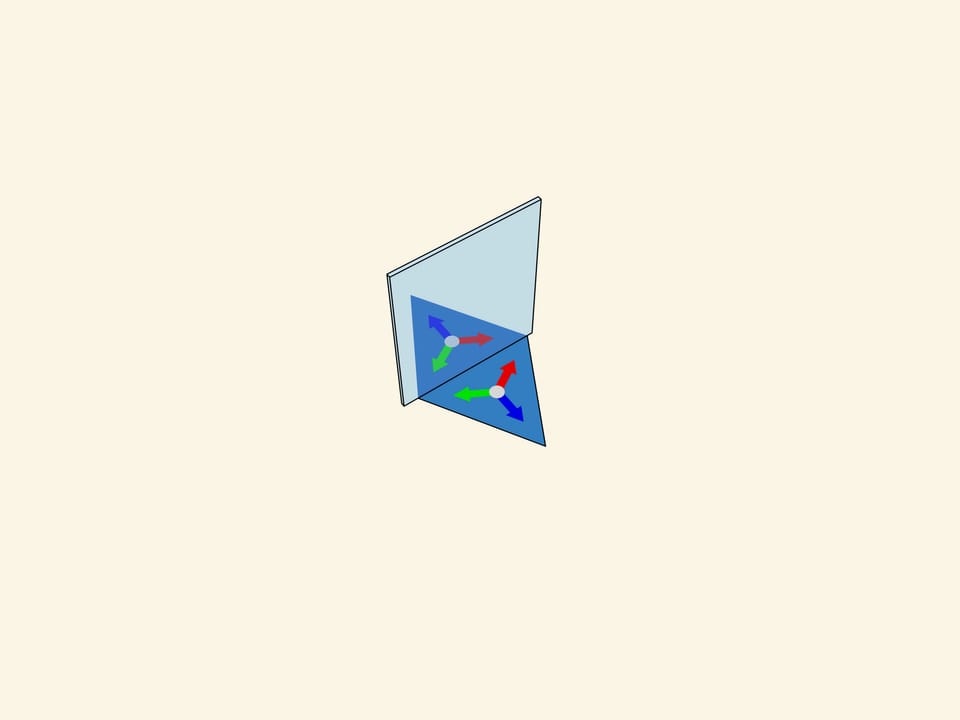
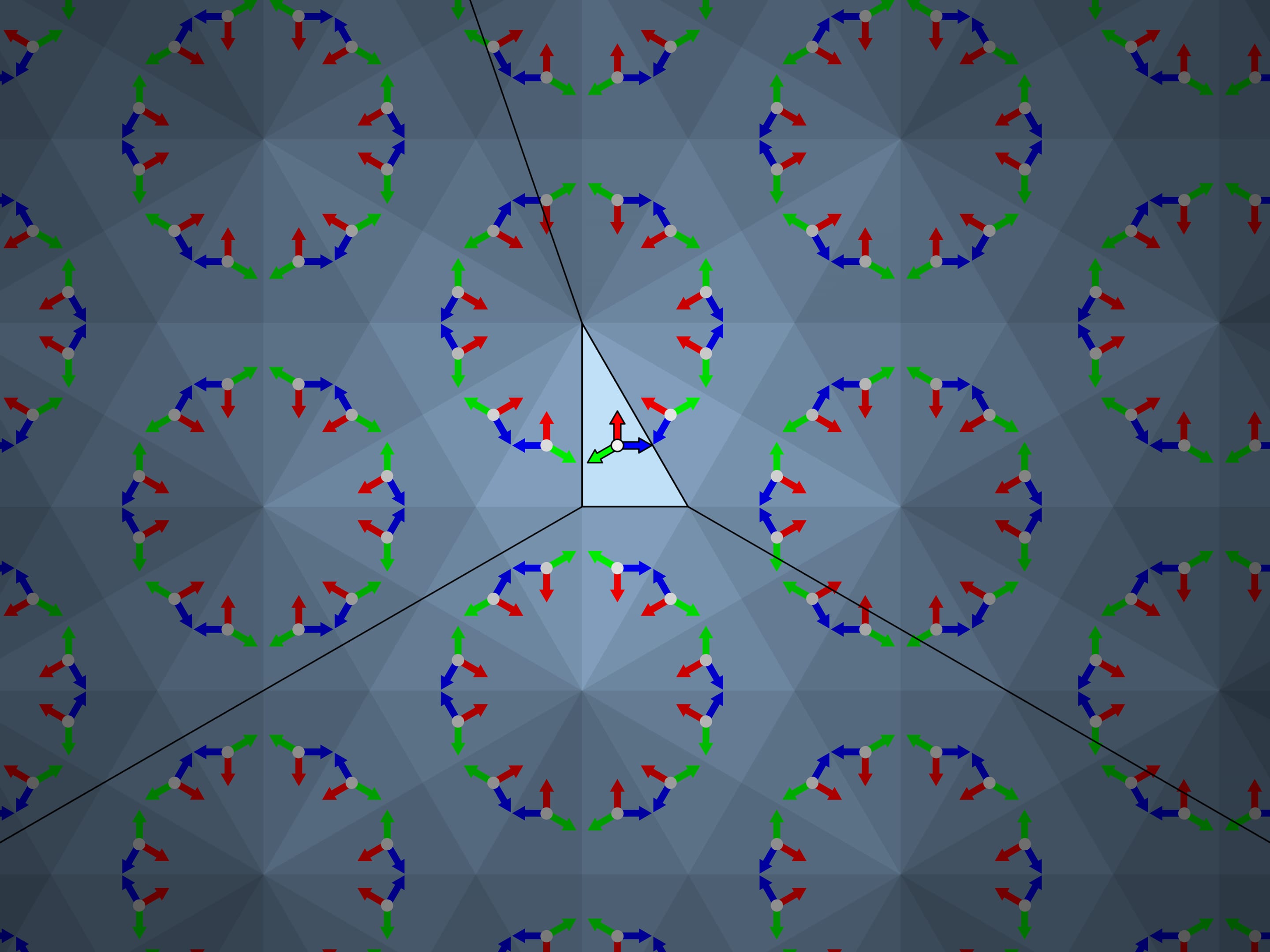
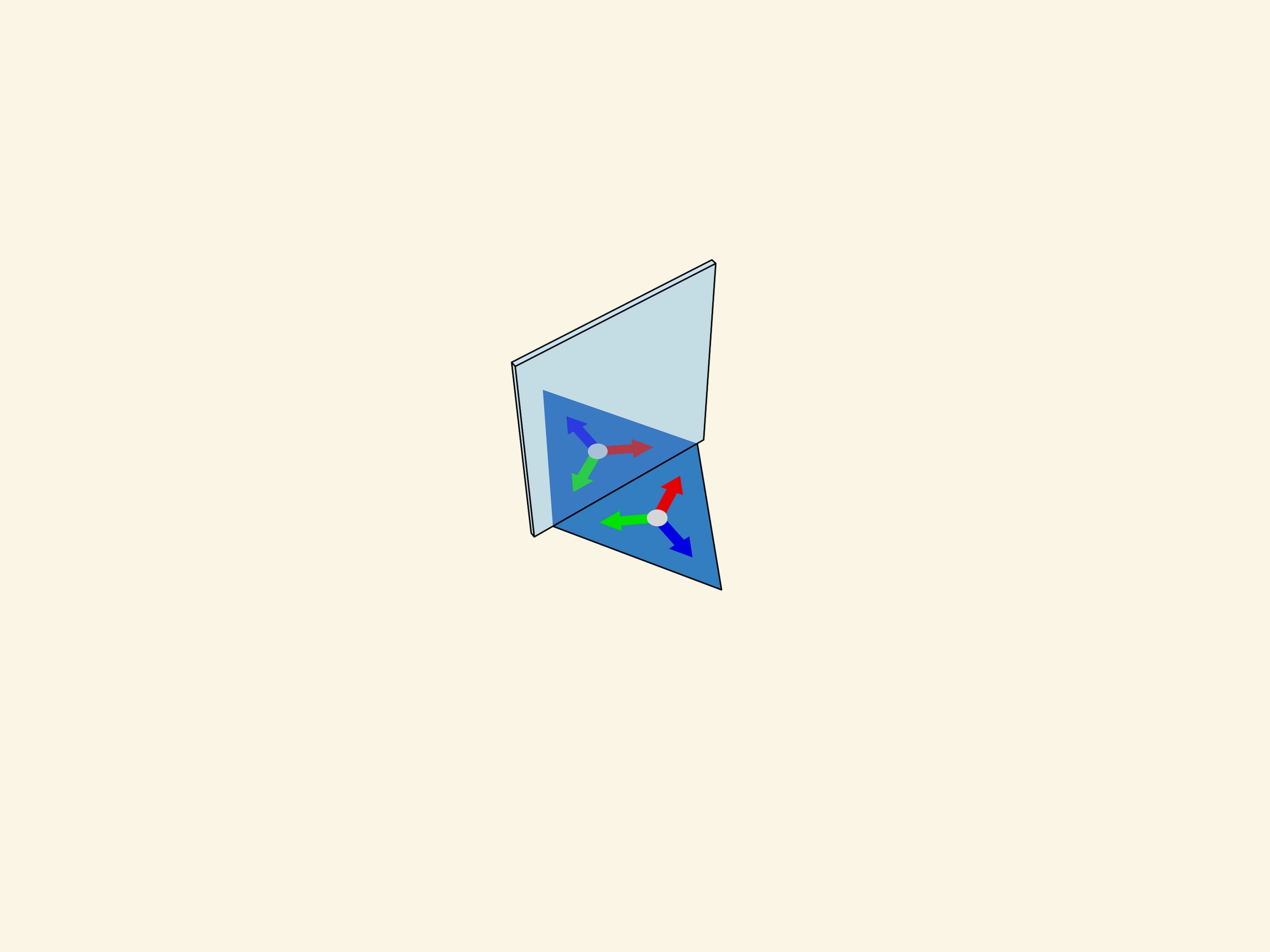
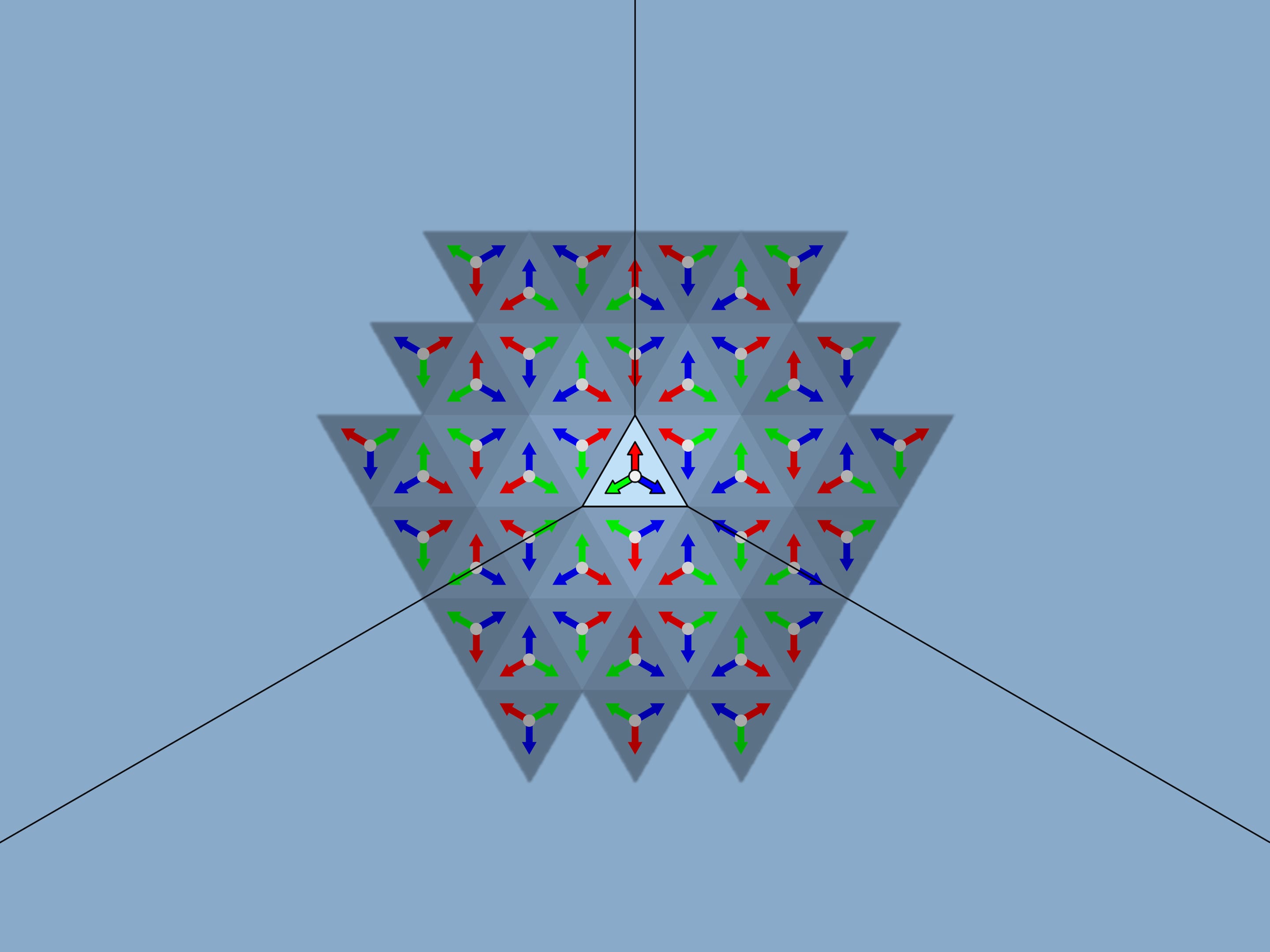
Let’s take the standard fundamental triangle with angles $60^\circ $—$60^\circ $—$60^\circ$. In mathematical terms, what does the physical reflection of a triangle in a mirror containing its side and perpendicular to its plane mean? It is the addition of a triangle symmetric to the original triangle relative to the side along which the mirror is placed. If we had a single mirror, this would be the end of it; the whole image would consist of the fundamental triangle and its image in the mirror. But in the case of kaleidoscope all three sides of the fundamental triangle are mirrored, so the observer will certainly see the fundamental triangle itself and its three copies symmetric relatively to its sides. In fact, as we know from experience, the image will be much bigger.
The truth is that mirror reflections in a mirror once again “work” like a mirror. So nature continues to reflect copies of triangles symmetrically relatively to their “virtual” sides.
That is the first condition on the fundamental triangle: with sequential symmetries relatively to all its sides and then the sides of its copies, the images must sweep (cover without overlap) the whole plane. At the same time, the order in which the reflections are made during sequential construction of the image should not affect the final result — our eye sees all the rays forming the reflections of the first order, the reflections of the second order, etc. at once.
The image observed in a traditional equiangular kaleidoscope is indeed the same as that obtained by the mathematical method discussed. And it is stable: if you sway the kaleidoscope, the image will not change. Even where an edge between the mirrors of the kaleidoscope moves relatively to the image, the image remains static regardless of the position of the kaleidoscope and its edges.
Kaleidoscopes built on fundamental triangles with angle sets $90^\circ $—$45^\circ $—$45^\circ$ and $90^\circ $—$30^\circ $—$60^\circ$ also satisfy all the described properties. Are there any other cases?
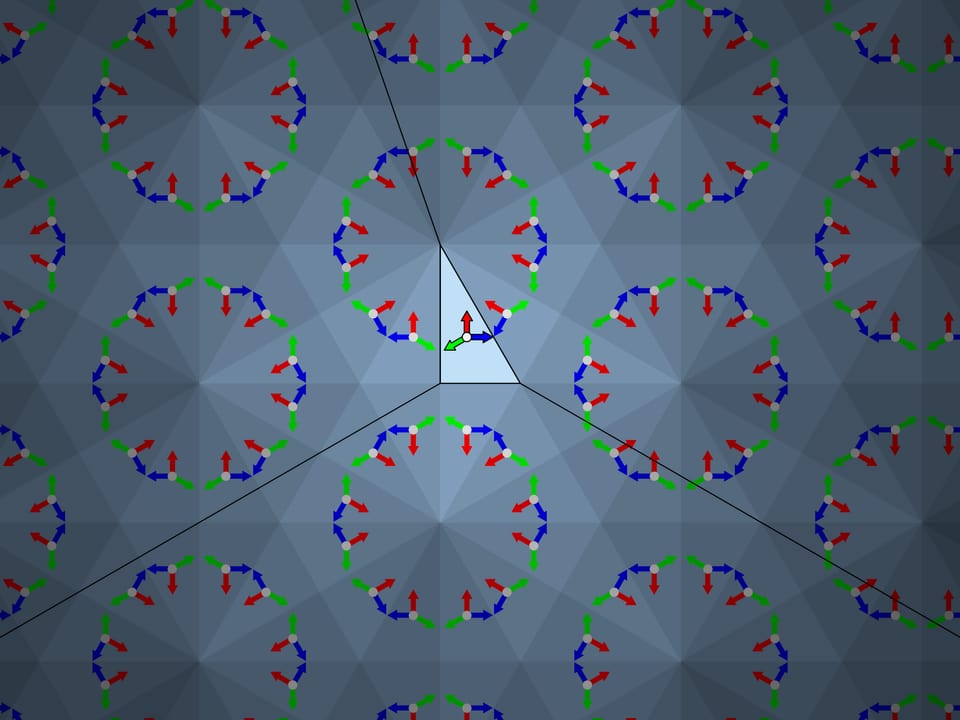
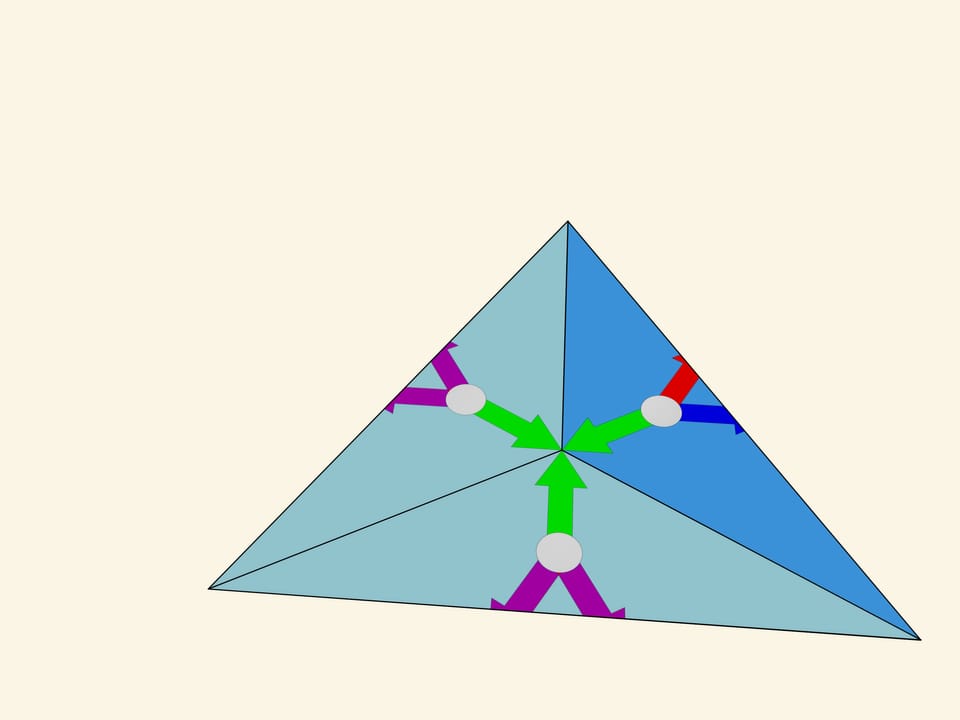
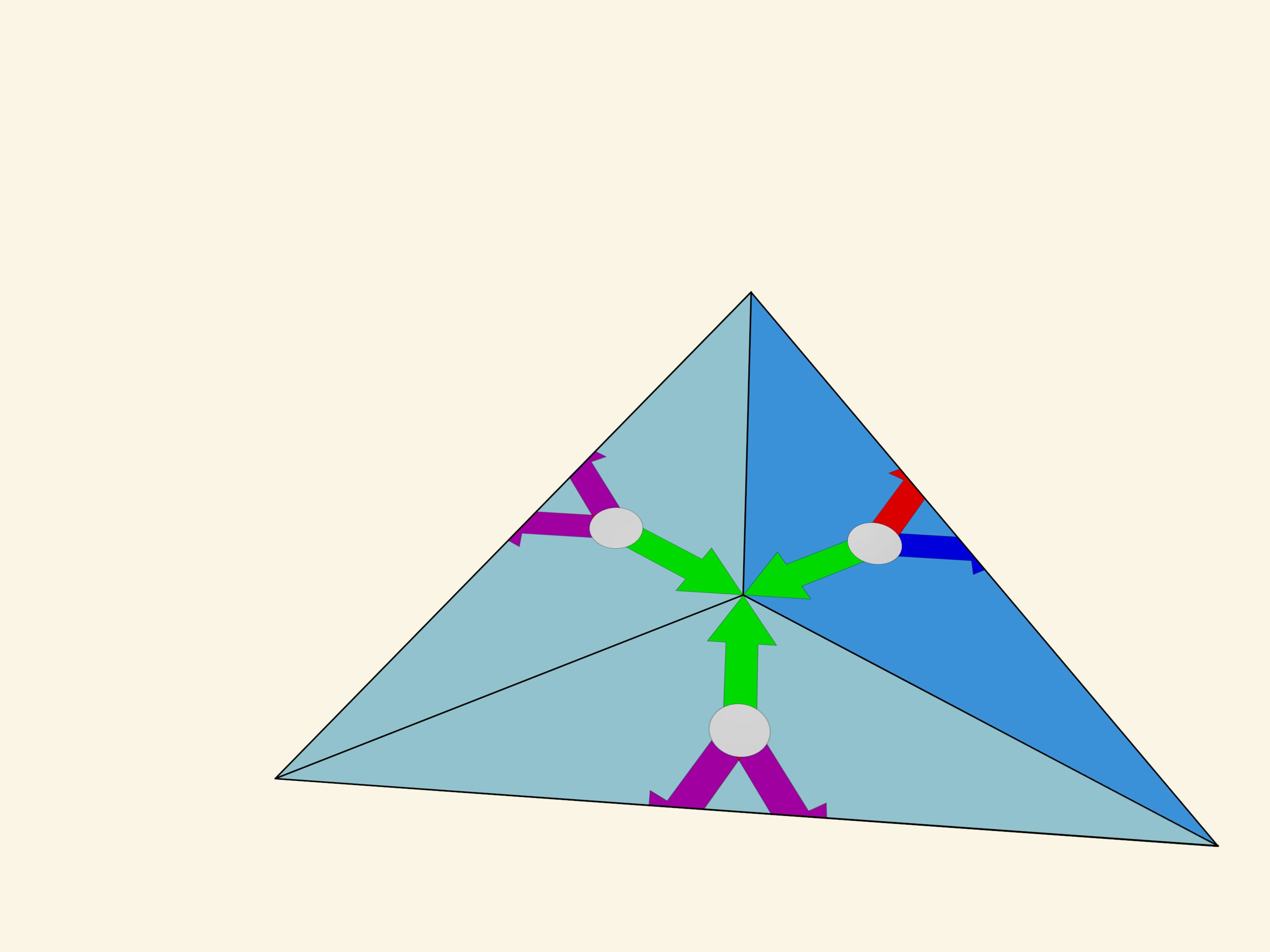
Consider a triangle with angles $120^\circ $—$30^\circ $—$30^\circ$. Geometrically this triangle seems to be suitable, the reflections relative to its sides produce a plane tiling. But let us start reflecting... An attentive observer may notice that even in the reflections of the first order — relative to the sides of the fundamental triangle itself — there is an inconsistency. The images obtained by the reflections with respect to the sides adjacent to the $120^\circ$ angle are not symmetric. Thus the image obtained by mathematical construction depends on the order in which the reflections are made. Specifically, if all possible reflections are considered, the image will be the “sum” of the original image and its mirror copy.
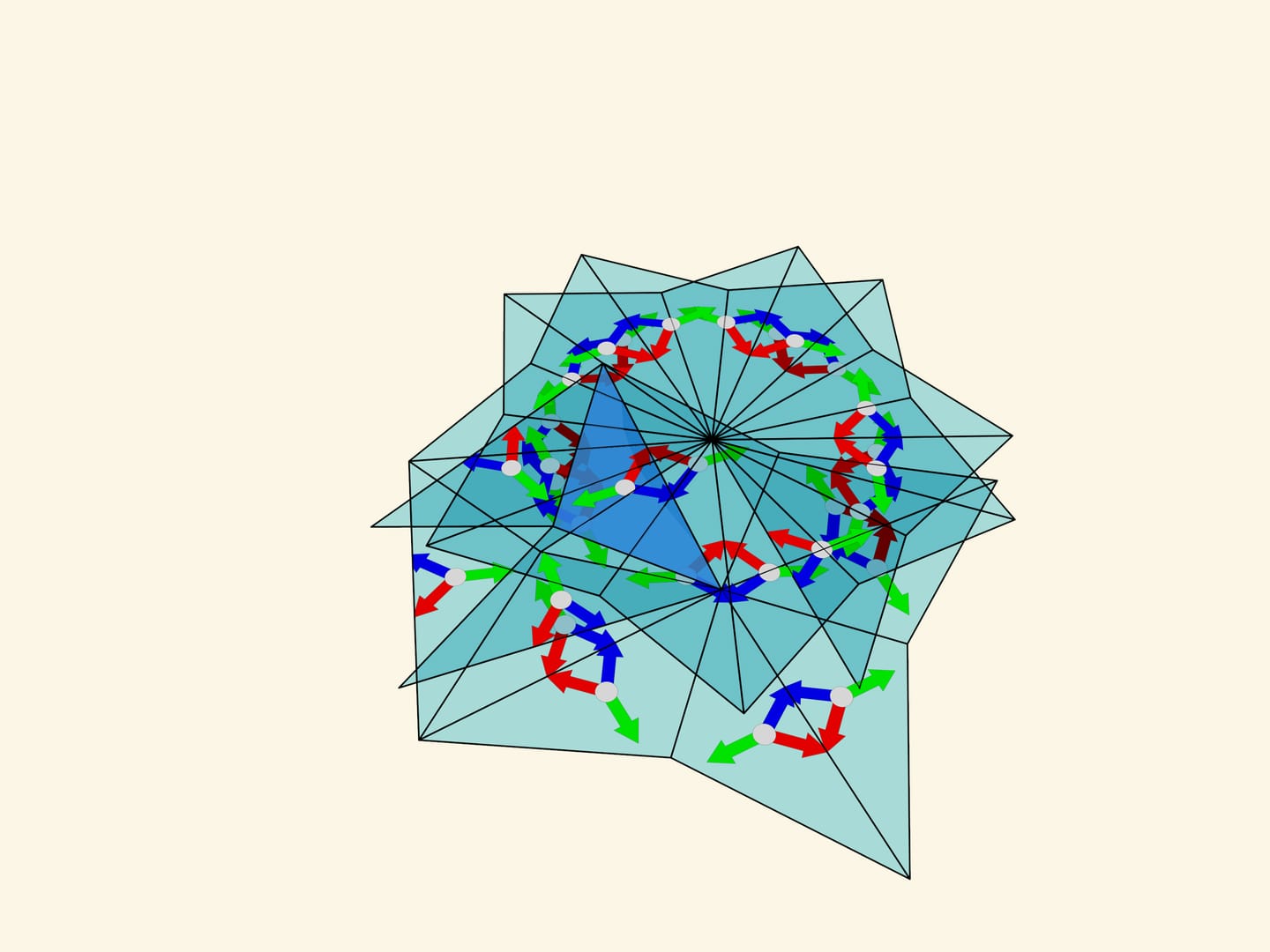
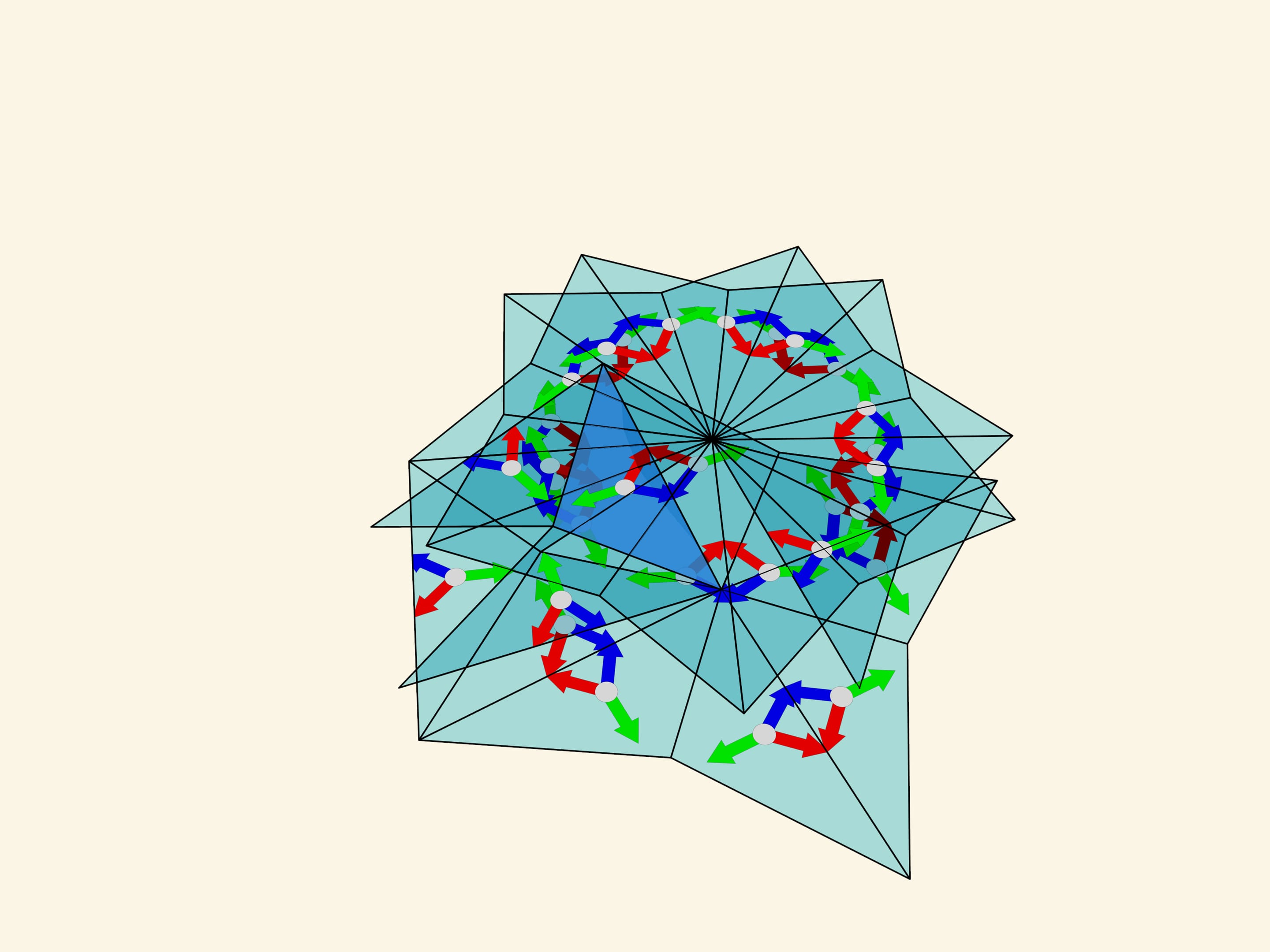
The surprises of the $120^\circ $—$30^\circ $—$30^\circ$ triangle don’t end there. If you make a kaleidoscope with these angles, at first sight it would seem that, unlike the mathematical construction which says that the image will, albeit well, overlap, the resulting optical system, gives a beautiful image. However, that is not true. We notice that even the simplest image (colored arrows perpendicular to the mirrors) is reflected unequally even in small orders of reflection. Somewhere the arrows of one color are seen near the centers of the formed hexagons, and somewhere the arrows of another color. Moving farther away from the fundamental triangle, there are other irregularities. So the real image does not coincide with the mathematically predicted one. The fact is that the image is formed in each of the mirrors separately according to the already mentioned principle “the image of the mirror in the mirror, works like a mirror again”. But the image formed in one of the mirrors is not re-reflected in the other mirror.
If we sway a kaleidoscope built on a fundamental triangle with angles $120^\circ $—$30^\circ $—$30^\circ$, we see that the image depends on the mutual position of the observer and the kaleidoscope axis — the image changes near the mirror prism edge as we sway.
In the case of an arbitrary triangle, if you start making all kinds of reflections of it on the plane, they will overlap each other and you can’t speak about any beautiful image. If one builds an optical system as a mirror prism over such a triangle, the whole image will be composed of somehow shuffled fragments of the original image and will not be regular.
So, a kaleidoscope can be constructed using a triangle with angles $60^\circ $—$60^\circ $—$60^\circ$, $90^\circ $—$45^\circ $—$45^\circ$ or $90^\circ $—$30^\circ $—$60^\circ$ as the base of the prism. How can we mathematically understand that a triangle with angles $120^\circ $—$30^\circ $—$30^\circ$, suitable geometrically for plane tiling using symmetries, is not suitable for constructing a kaleidoscope? Are all possible triangles already listed?
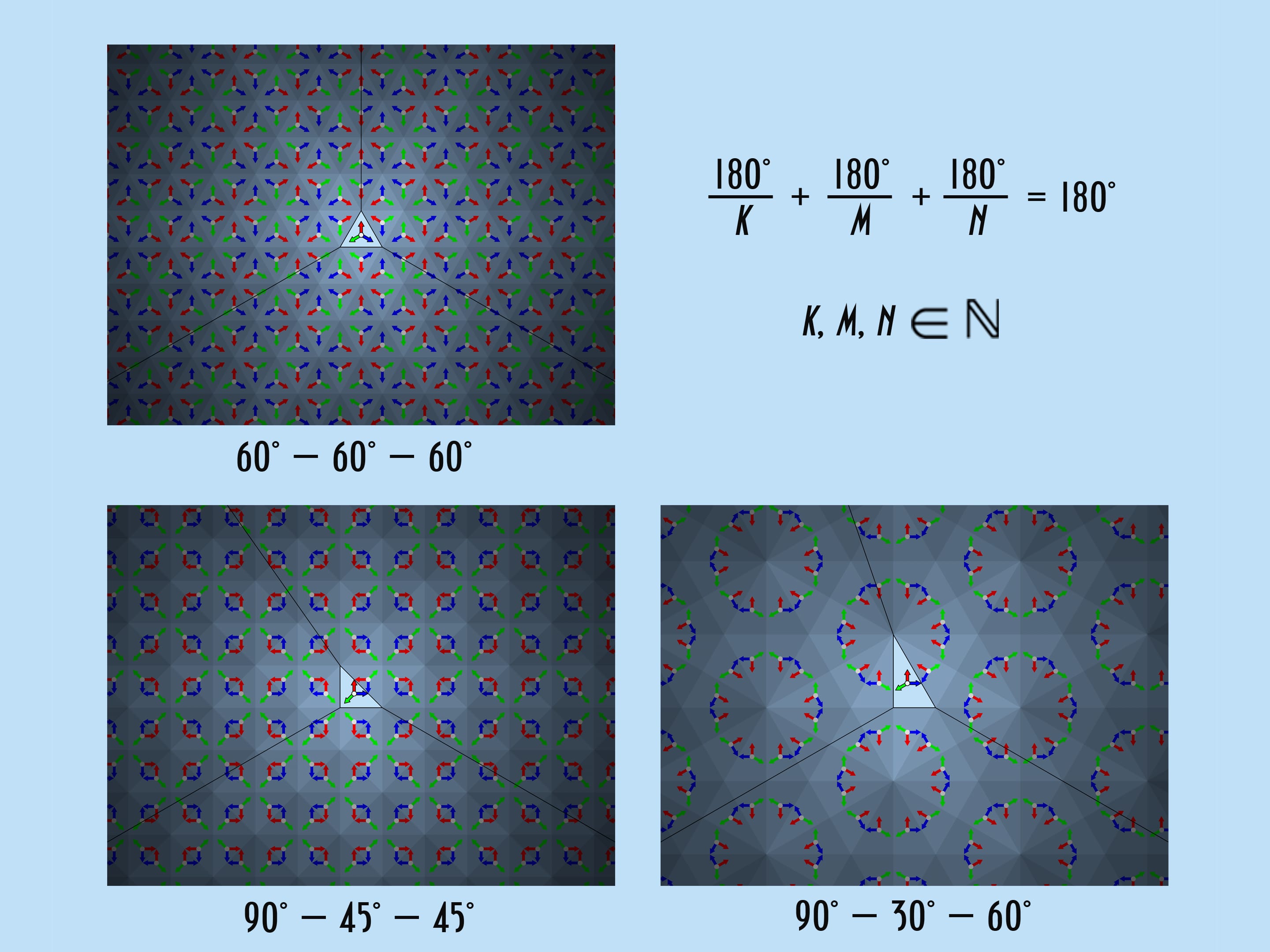
The requirements on the resulting image in the kaleidoscope can be stated explicitly: The triangle at the base must have angles $\frac{180^\circ }{k}$, $\frac{180^\circ}{m}$, $\frac{180^\circ}{n}$, where $k$, $m$, $n$ are natural numbers, and $\frac{180^\circ}{k}+\frac{180^\circ}{m}+\frac{180^\circ}{n}=180^\circ$. If we ignore the order, the only solutions $\{k, m, n\}$ of this equation are the triples $\{3, 3, 3\}$, $\{2, 4, 4\}$ and $\{2, 6, 3\}$, giving the already familiar sets of angles $60^\circ $—$60^\circ $—$60^\circ$, $90^\circ $—$45^\circ $—$45^\circ$ and $90^\circ $—$30^\circ $—$60^\circ$. There are no other “kaleidoscopic” triangles.
If the base of the mirrored prism is not a triangle but an arbitrary polygon, the right kaleidoscope is only possible by using four mirrors placed at the sides of the rectangle.
This reasoning about the principle of kaleidoscope is the starting point of a very interesting area of mathematics, the theory of reflection-generated groups.