Lipkin linkage⁠

Since James Watt invented the steam engine there was a problem of trans­forming rotary motion of one hinge into perfect straight-line motion of another. Thus, a straight-line mech­a­nism.

During a long time scien­tists and engi­neers couldn't solve this problem, were constructing approx­i­mate solu­tions drawing not perfect straight lines. And only beau­tiful math­e­matics helped finally to solve this problem.

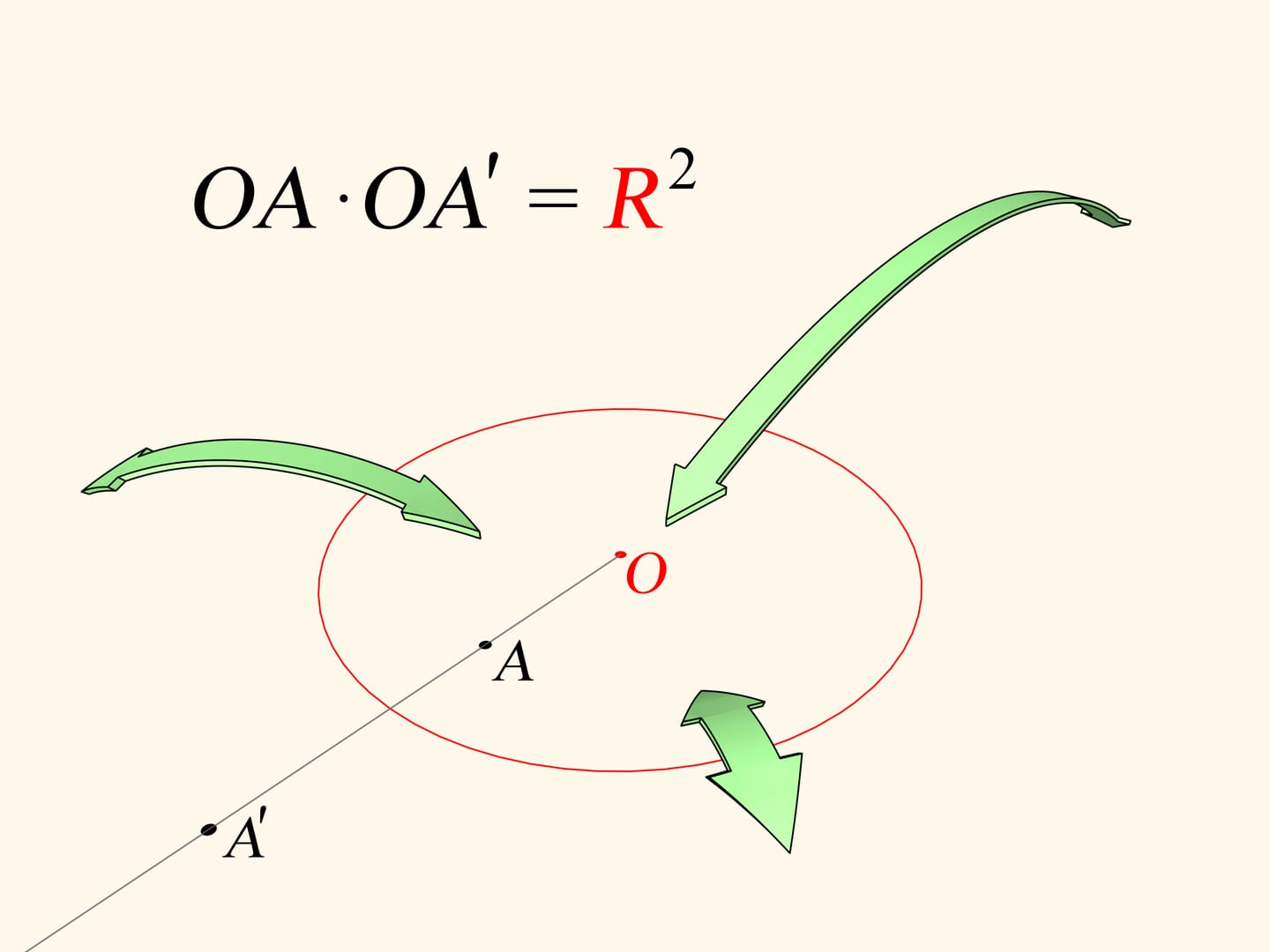
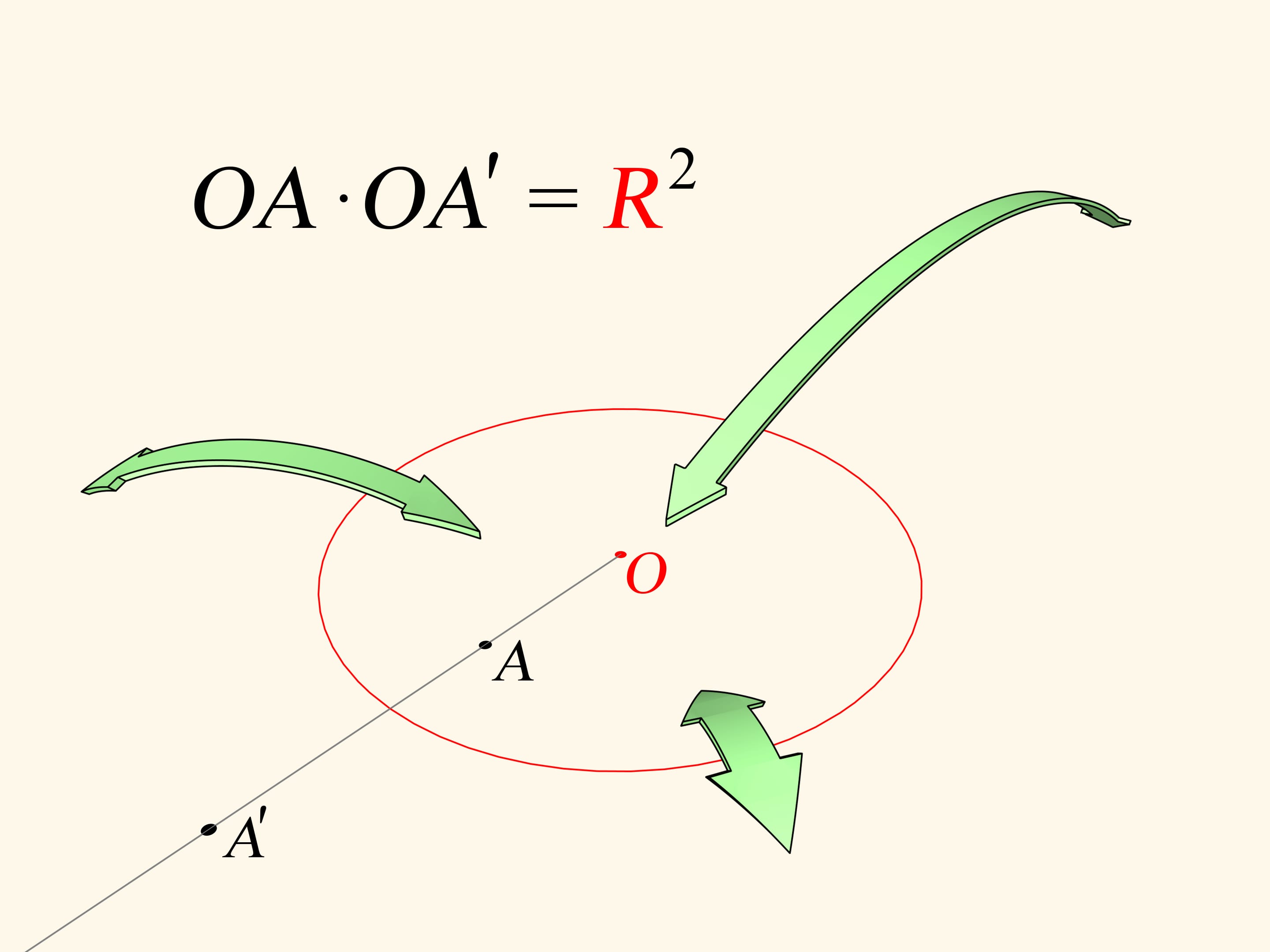
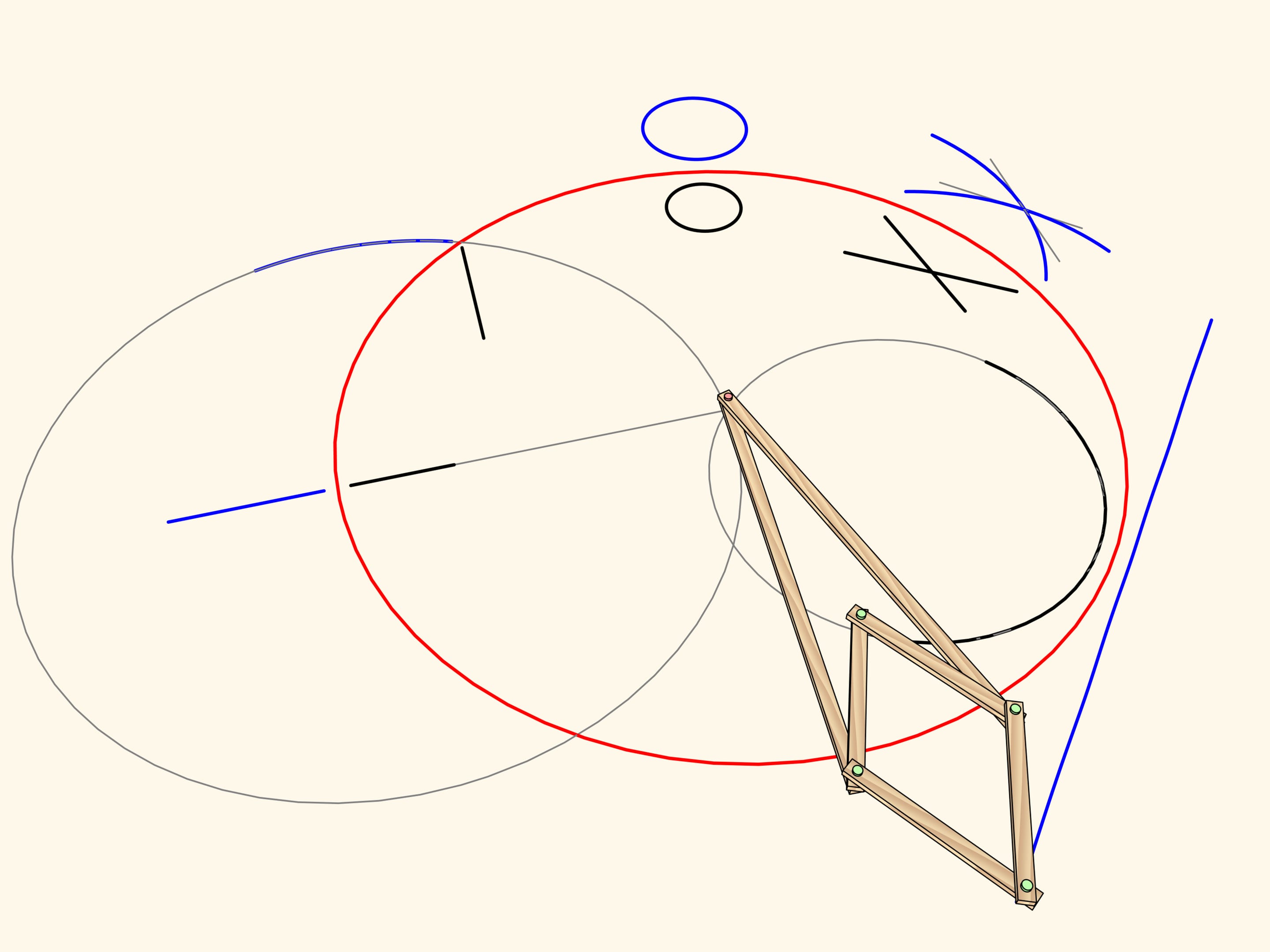
Let's recall that plane circle inver­sion is a bijec­tive mapping of the inner part of the circle (except a single point, the center) onto the outer part. The image of the point $A$ is the point $A’$ lying on the ray starting at the center and passing through $A$. Its posi­tion is deter­mined by the equality $OA \cdot OA'=R^2$. Inver­sion helps to solve many inter­esting prob­lems in geom­etry. As we'll se, it helps not only in theo­ret­ical ques­tions.

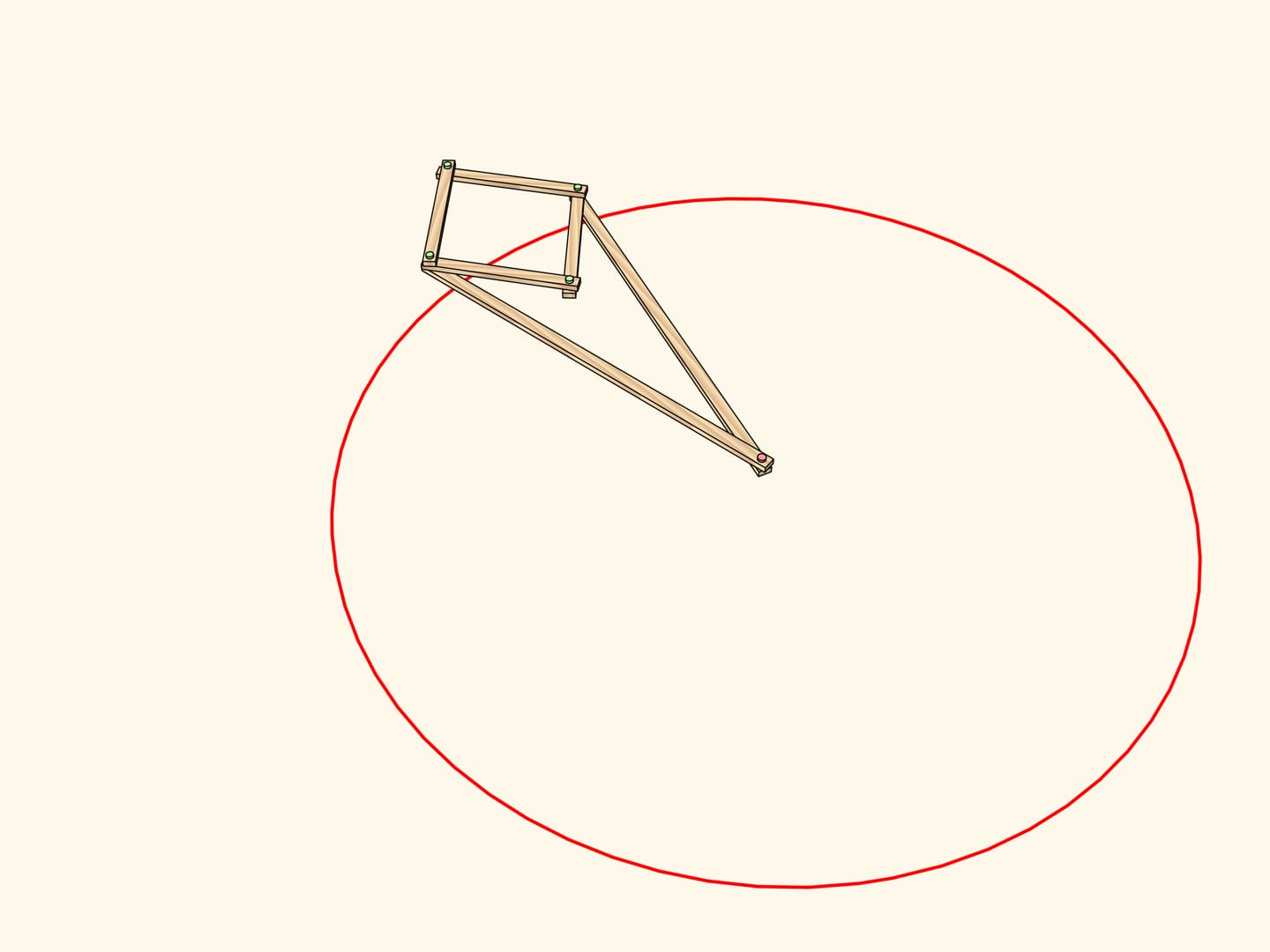
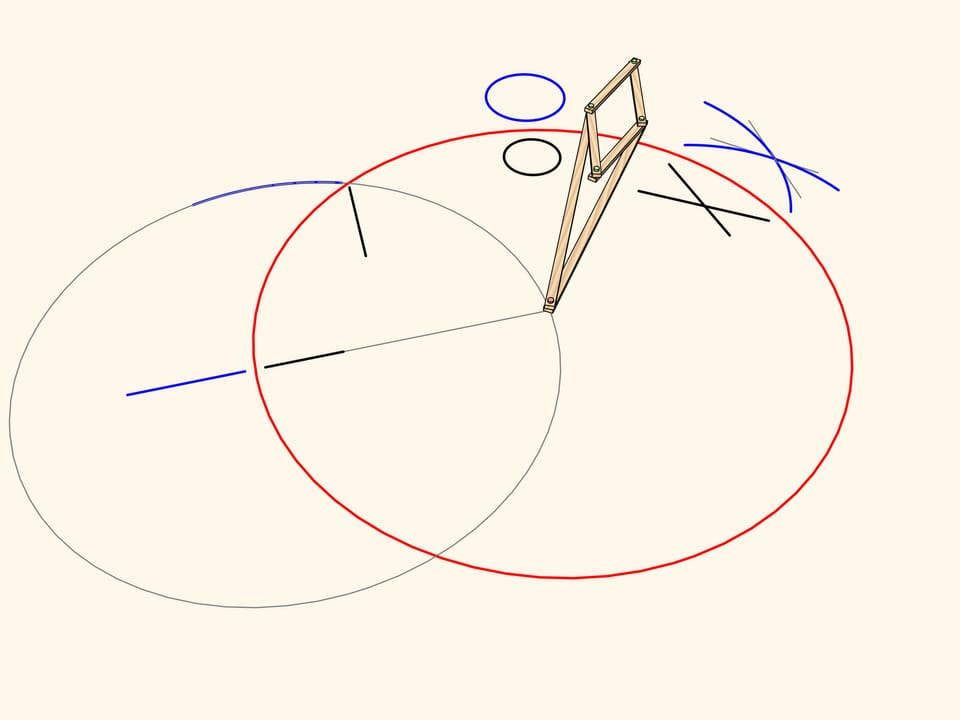
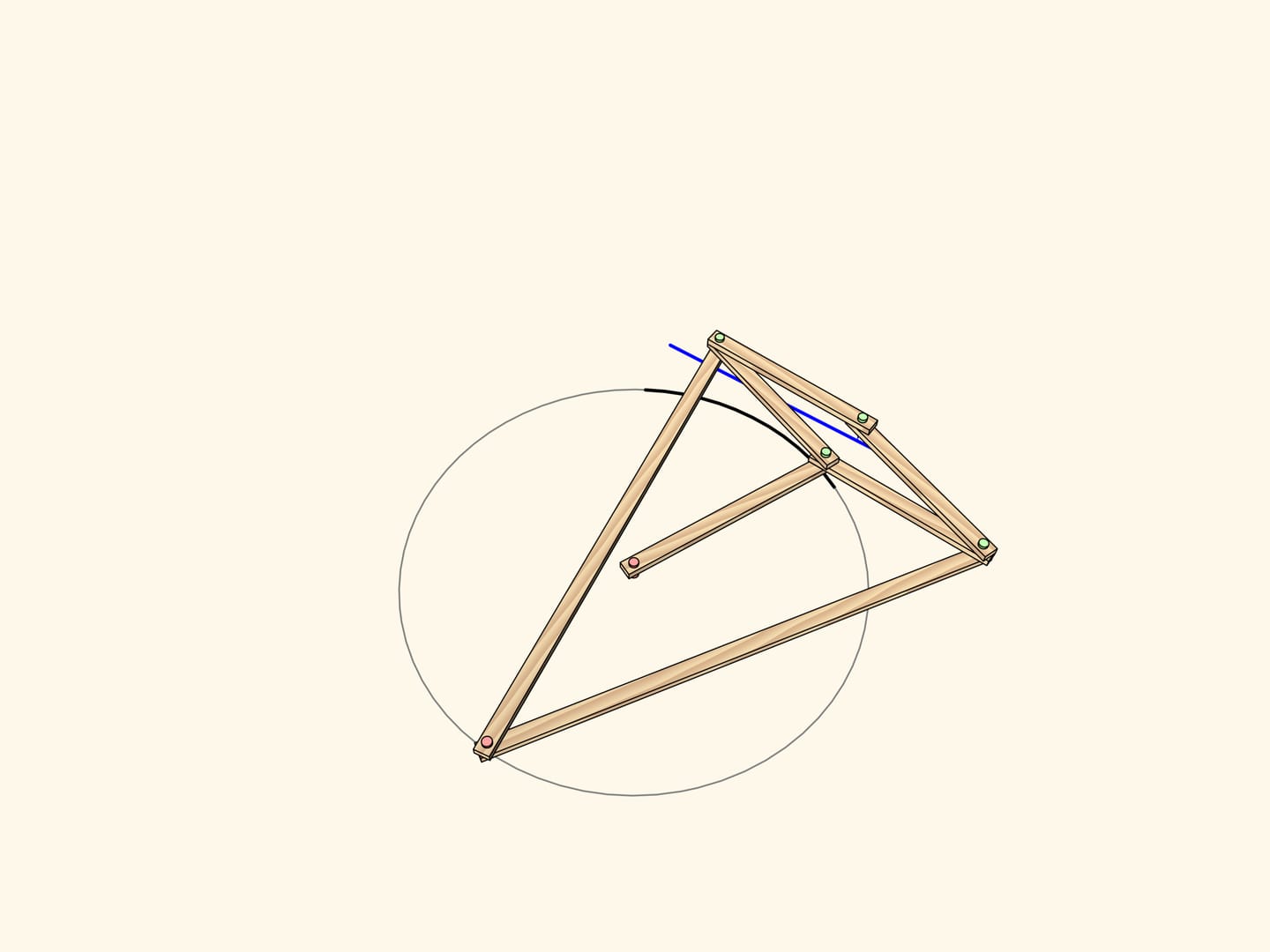
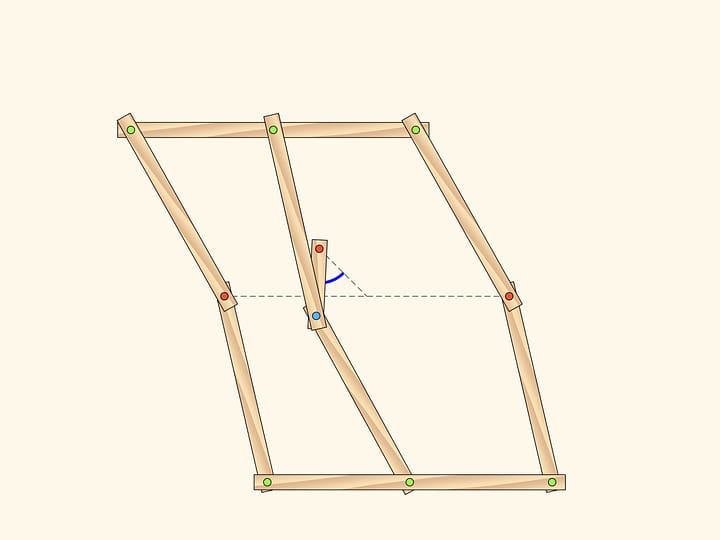
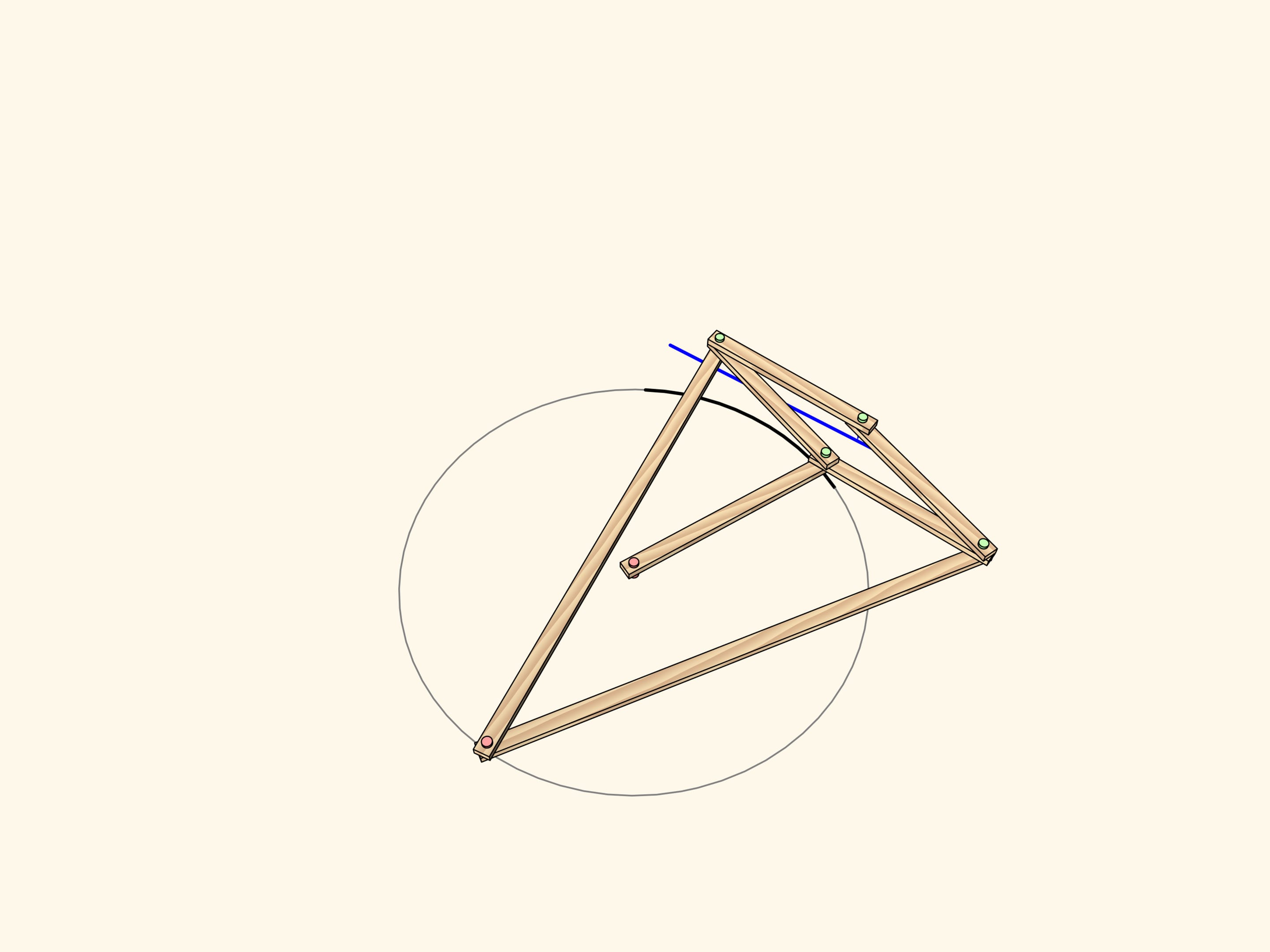
Consider a linkage with one fixed red hinge. The ends of two equal edges are attached to a hinged rhomb.

This mech­a­nism imple­ments inver­sion with respect to a circle centered in the fixed hinge and radius depending on the edge lengths.

Let's see using our mech­a­nism what prop­er­ties inver­sion has.

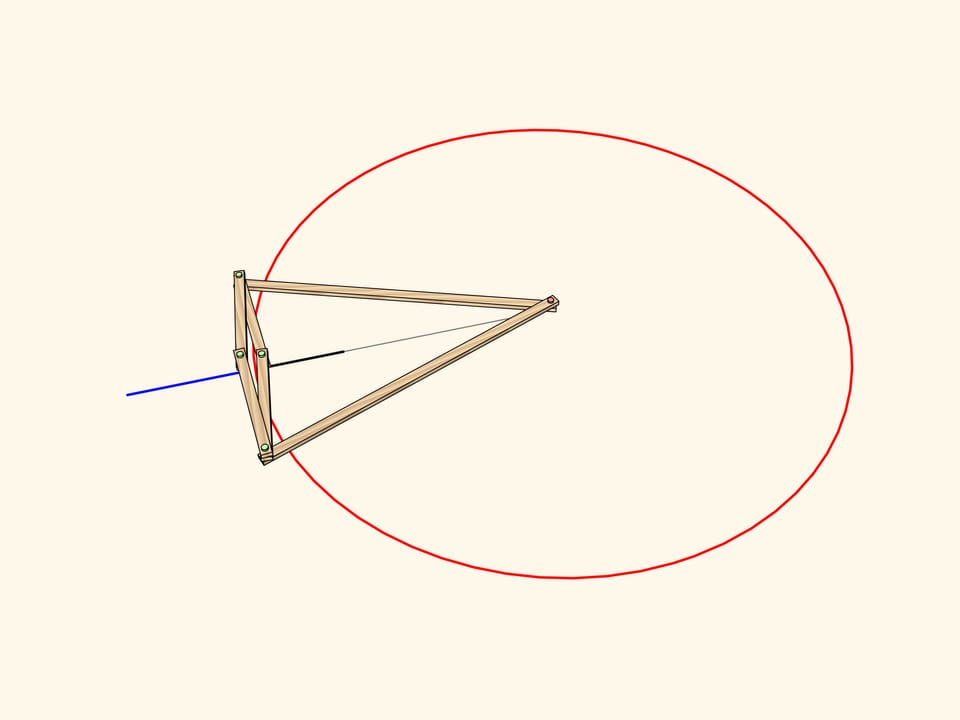
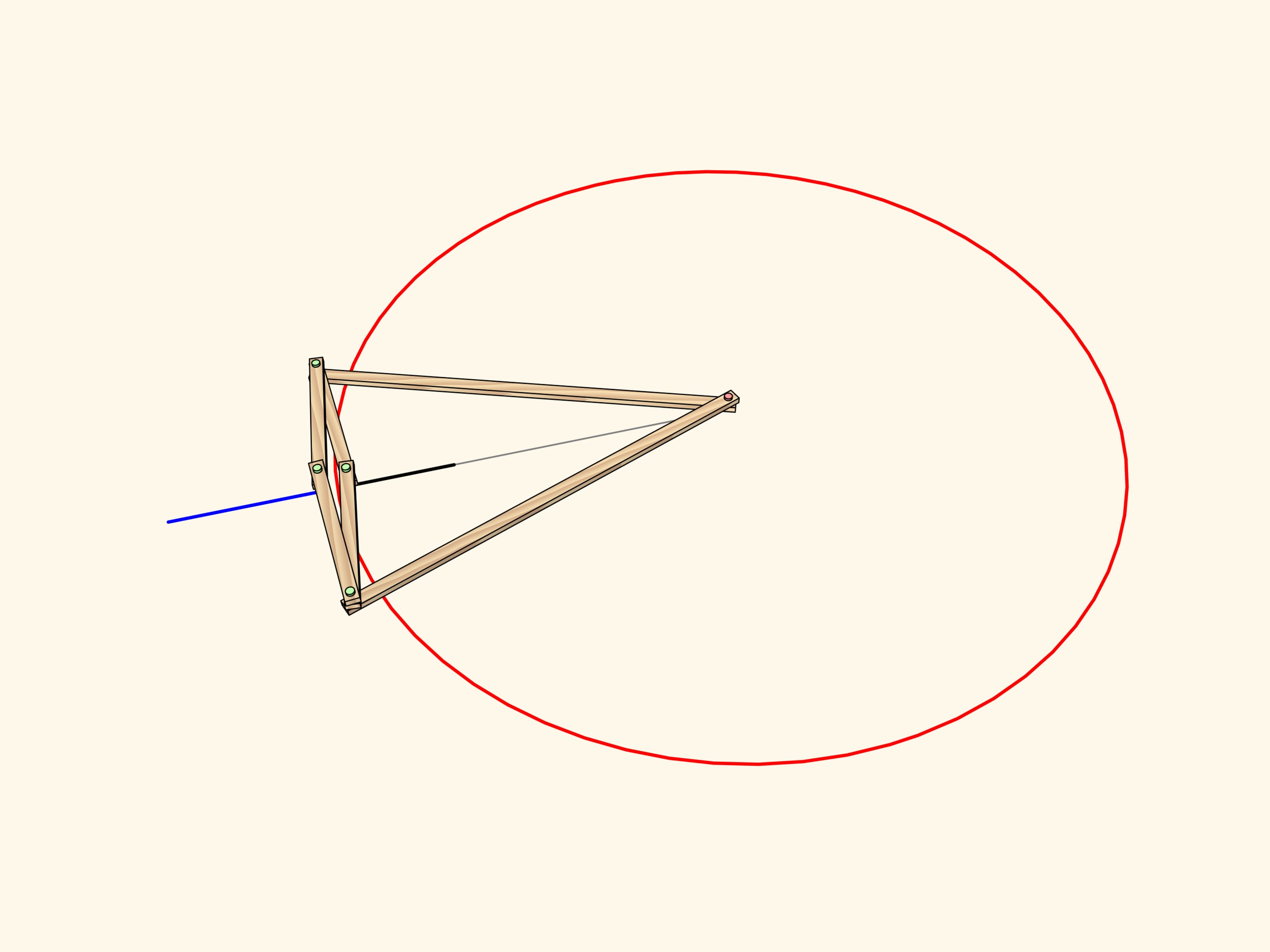
From the defi­n­i­tion of inver­sion it is clear that the image of a segment of a line passing through the center is mapped again to a segment lying on the same line.

The image of a segment of a line not passing through the center is an arc of a circle, passing through the center of inver­sion.

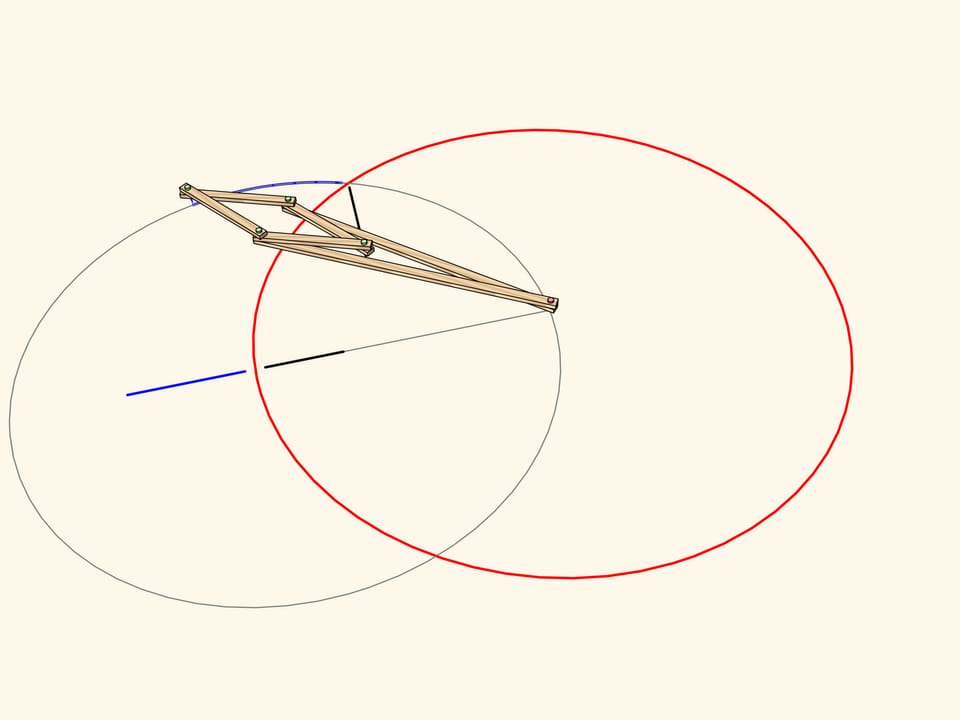
A circle not passing through the center of inver­sion and not inter­secting the inver­sion circle maps again to a circle.

Inver­sion changes orien­ta­tion. Similar trans­for­ma­tions in math­e­matics are called anti-conformal (conformal are those that preserve both angles and their orien­ta­tion).

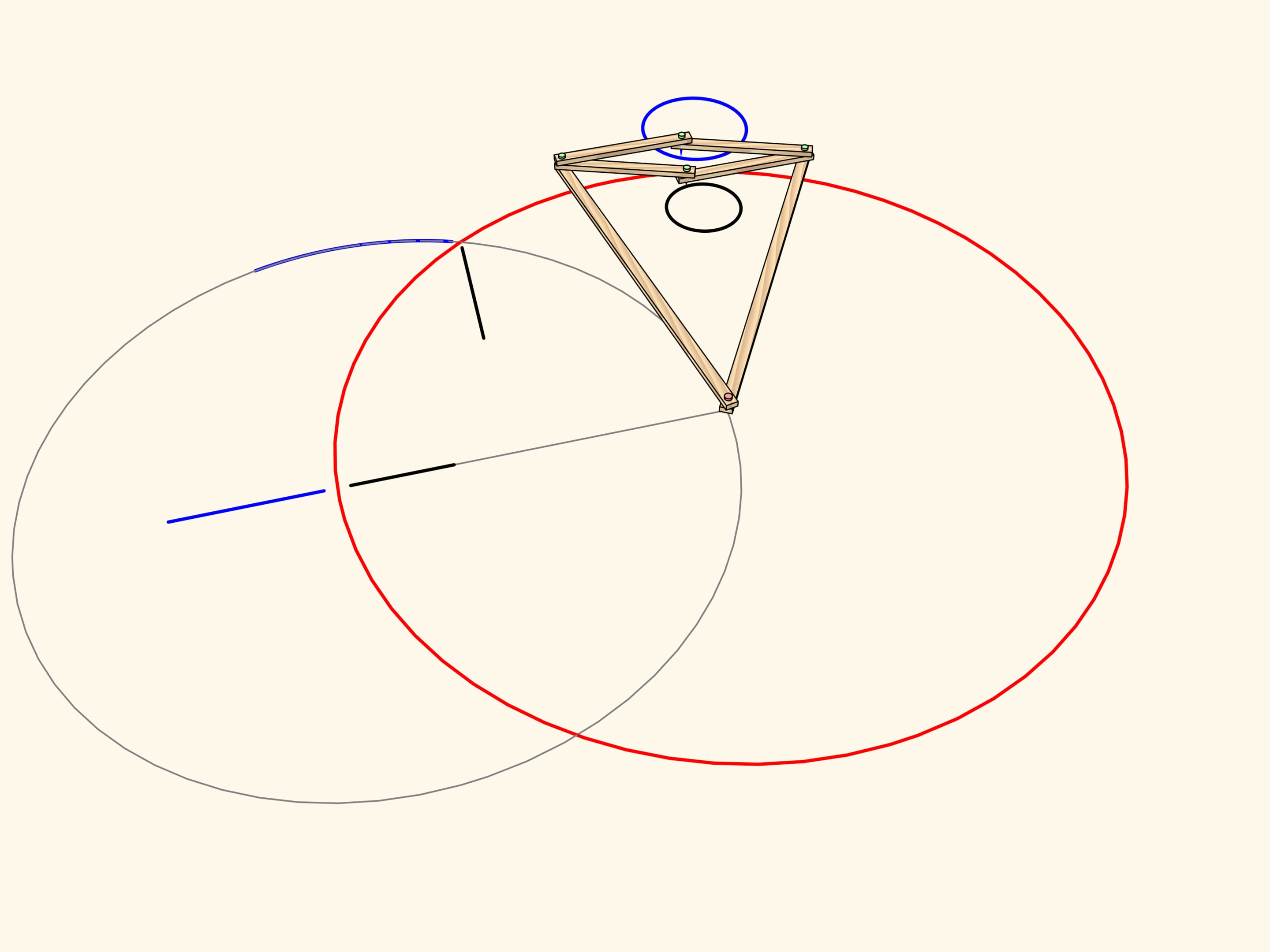
An arc of a circe passing through the center of inver­sion maps to… a strict straight-line segment!

Exactly this prop­erty has been used to construct the straight-line linkage. Add a fixed hinge in the center of the circle and an edge of radius length so that the leading hinge follows the circular path. Thus, the driven hinge will always follow a straight-line segment. This kind of mech­a­nisms are often called inver­sors.

In 1864 in a private letter an engi­neer of the French army Charles Nicolas Peaun­cel­lier (1823—1913) announced his construc­tion of an inversor. However, he didn't mention any details. In 1868 a student of P. L. Tcheby­shev, Lipman Lipkin (1846—1876), invents an inversor. His detailed paper was published in 1870 and only in 1873 Peaun­cel­lier publishes his one describing exactly the same mech­a­nisms and citing Lipkin.

After­wards, there were other link­ages constructed based on other math­e­mat­ical ideas. However, the inversor is notable for its beauty, good mechan­ical prop­er­ties and is widely used in tech­niques.