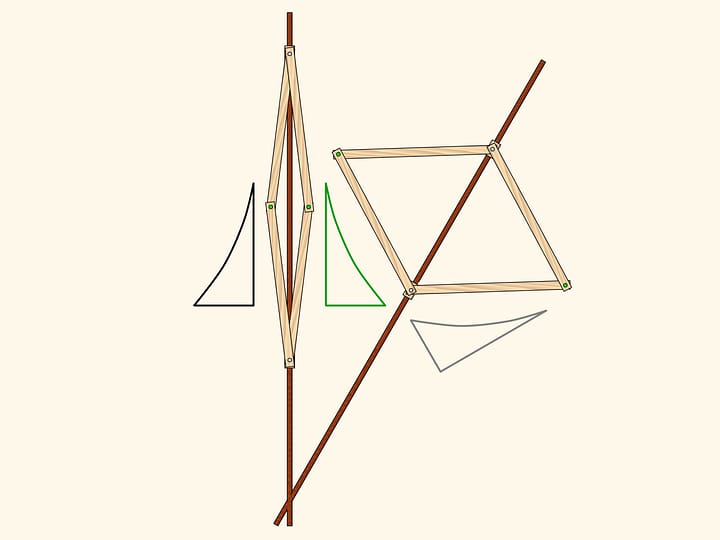
A parallelogram is a quadrilateral whose opposite sides are pairwise parallel. One of the few school definitions that we remember all our lives, and, as it turns out, for a good reasons — many objects around us work habitually due to the parallelogram properties.
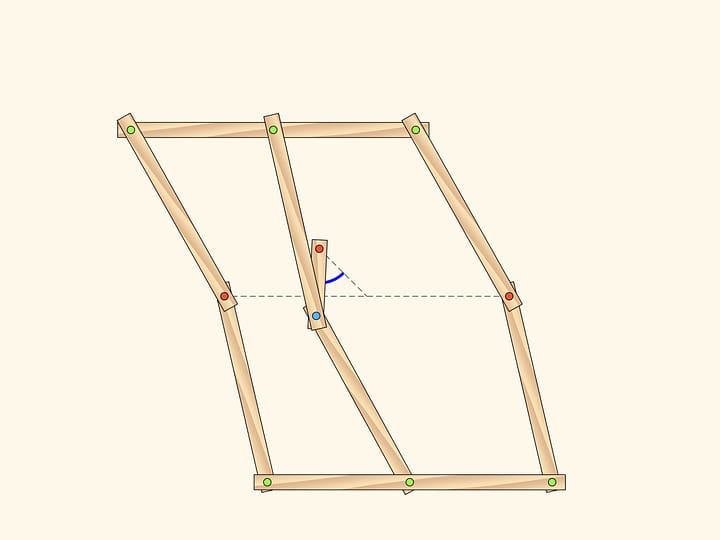
The equality of the parallelogram's opposite sides is already a consequence of the given definition, i.e. the parallelism of the sides. And even if you build a hinged parallelogram, for ex. using a child's building set, the sides will always remain parallel when the parallelogram is skewed. By the way, this simple model demonstrates that, unlike a rectangle, the parallelogram area is defined not by the sides' lengths alone: when skewed, sides' lengths don't change, but the area does.
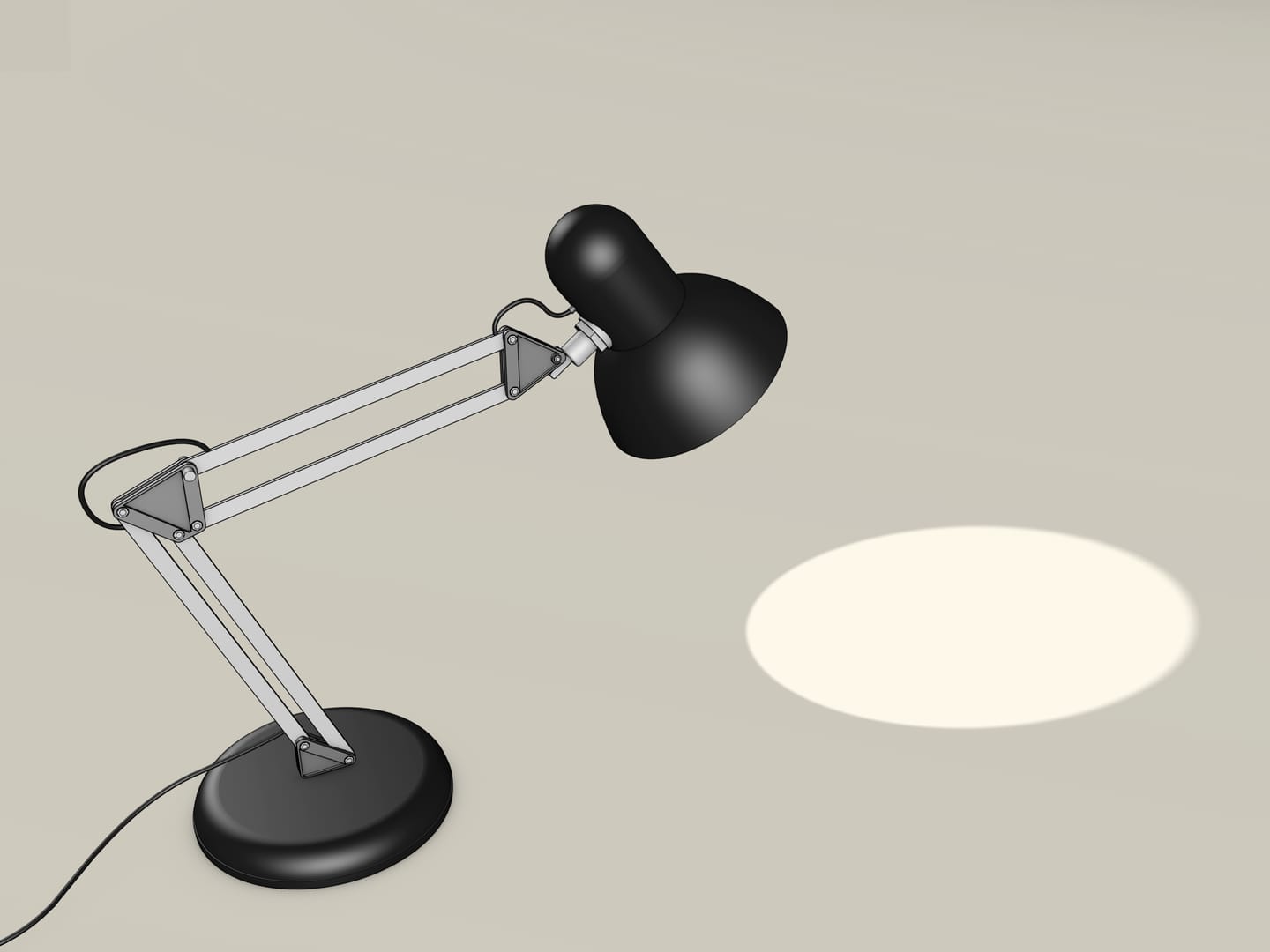
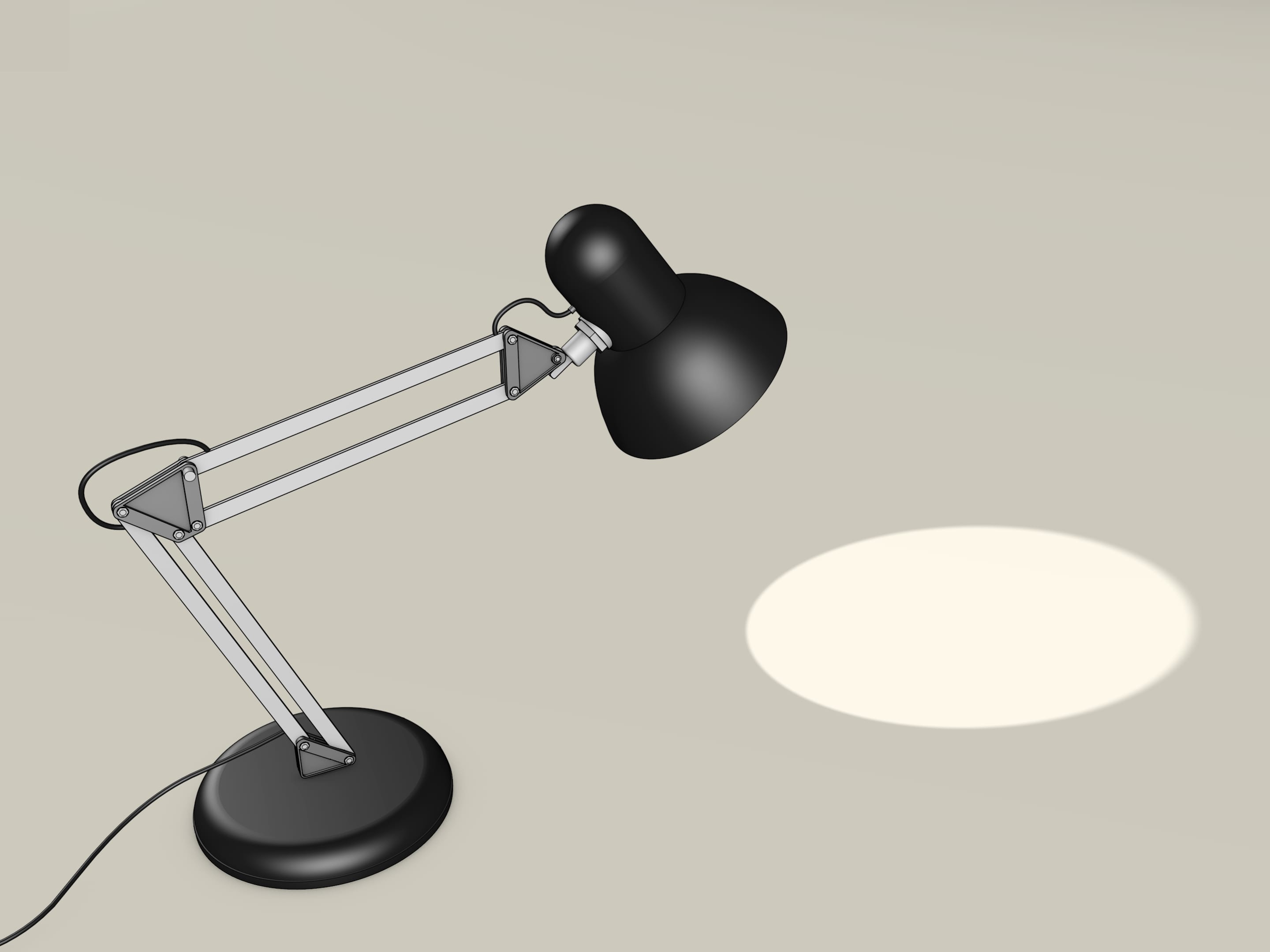
The desk lamp has a solid base and lampshade connected by one, but more often by two parallelograms. This design allows you to change the lamp position without changing it's tilt angle relative to the table. The same behavior has, for example, pantograph stands for studio microphones.
The hinged parallelogram allows you to change the position of the lamp while maintaining the tilt angle: the side of the parallelogram to which the lampshade is connected always remains parallel to the opposite side that does not change its direction. But if the stand is made as a single parallelogram, the movement of the lamp is predetermined — it may only move in a circle. A double (hinged) parallelogram — two parallelograms with a common side, or connected with a piece that doesn't change its geometry — allows you to maintain the lamp tilt angle and still move it to an arbitrary point in a fairly large area of space.
In 1669 at the Paris Academy of Sciences, Gilles Roberval demonstrated his balance whose readings remain independent of the item's position on its plates. By the way, it is the same Roberval who calculated the area under the arch of the cycloid, bringing that area to the area under the sine wave.
And the core of the Roberval balance is the hinged parallelogram yet again! Its sides, on which the plates are mounted, always remain vertical. Exactly due to the usage of the parallelogram, the balance's readings are independent of where on the plates the items are placed. Roberval himself, being both a mathematician and a mechanic, discovered this experimentally, and the strict kinematical proof did not appear until the beginning of the 19th century. Balance, as an important tool in the life of society, has been improved numerous times, and there are now numerous designs of different complexity. But most of them, in one way or another, to this day still use the properties of the parallelogram.
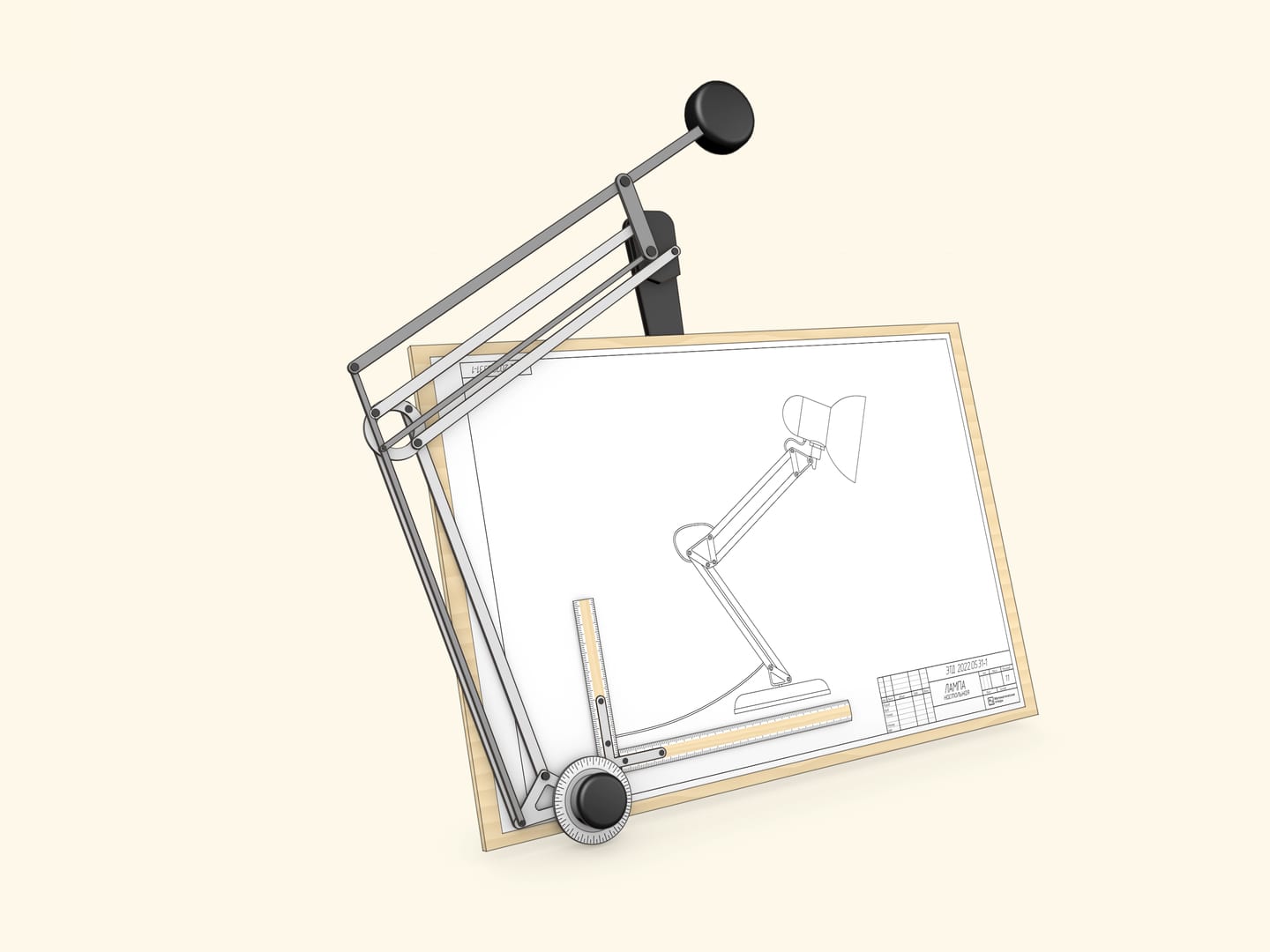
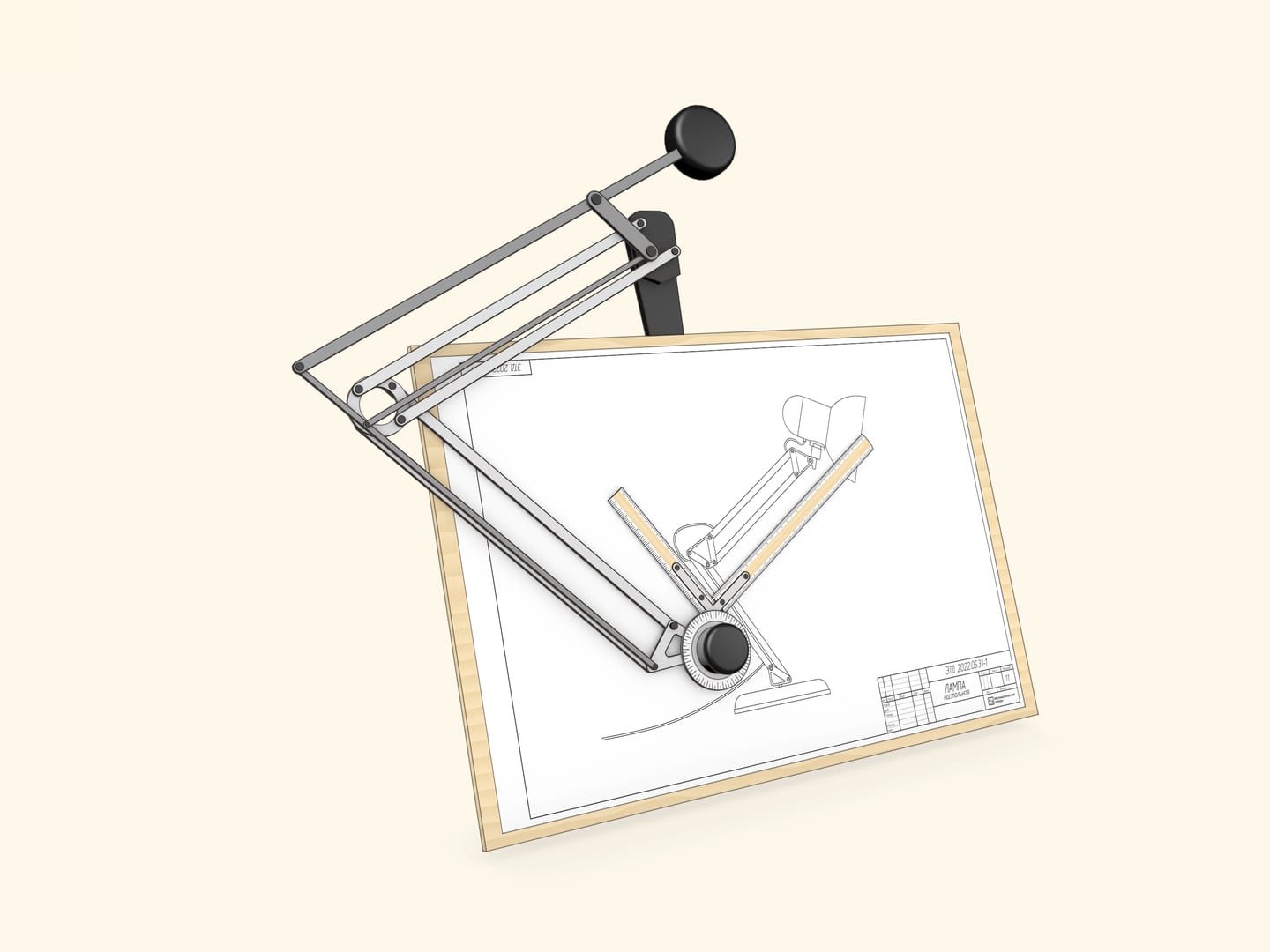
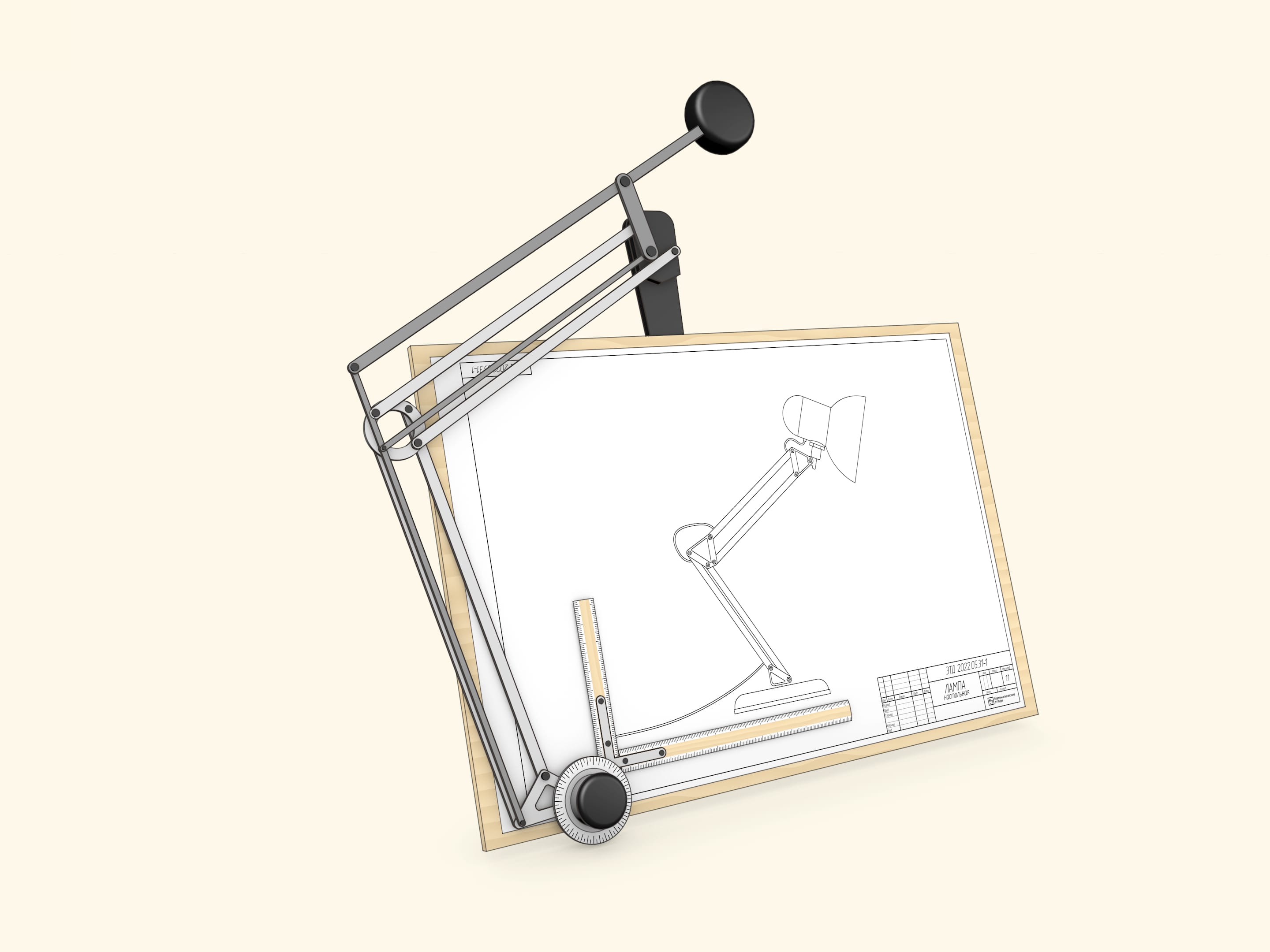
From the beginning of the 20th century until the advent of computers, the primary drawing tool for engineers all over the world was the drafting tables. This device consists of a drawing board and a drafting machine.
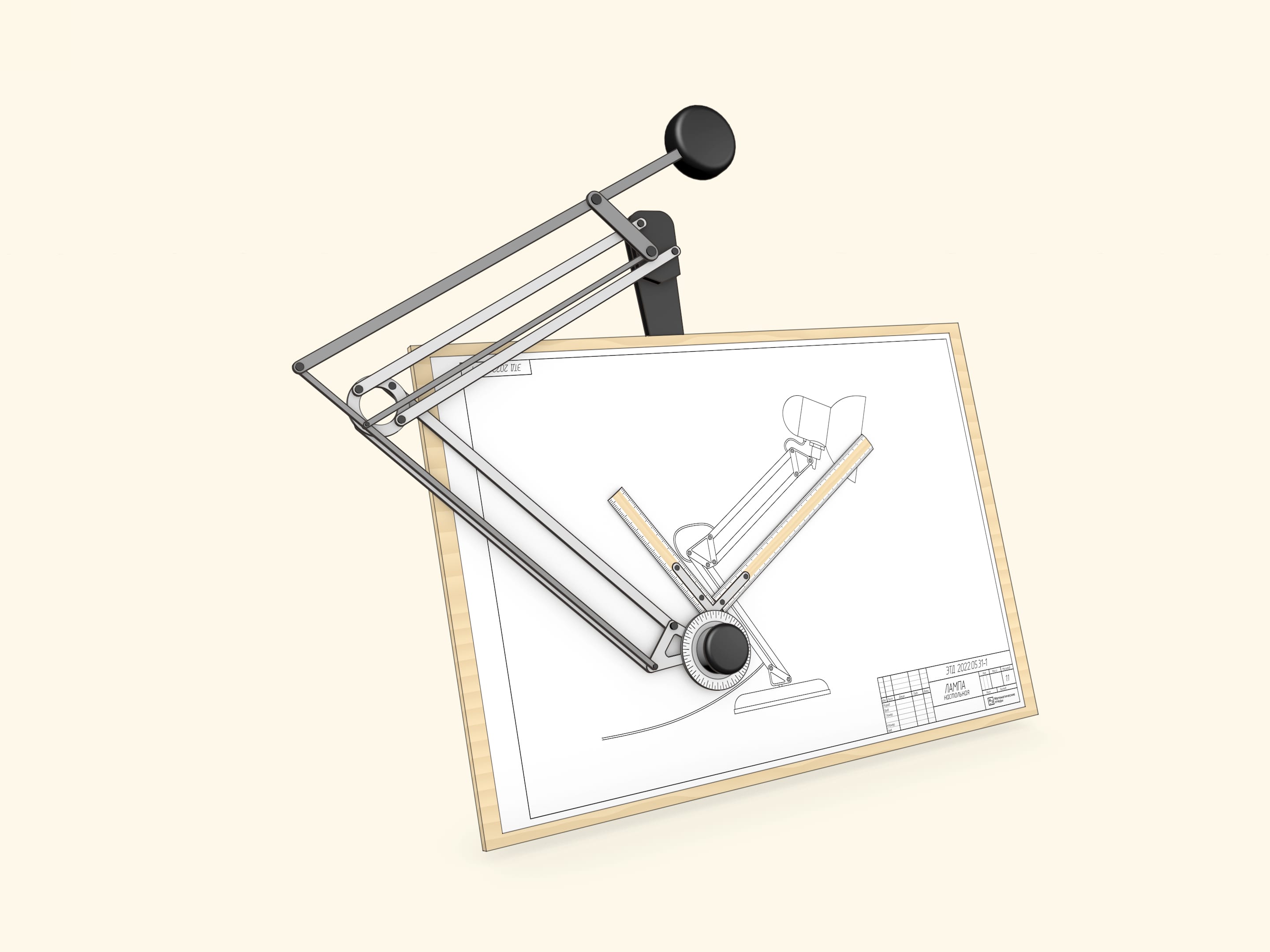
And the core of the drafting machine is (yet again) the double parallelogram. The double parallelogram, rigidly attached by one side to the drawing board and fitted with a pair of scales mounted to form a right angle on an articulated protractor head, allows you to draw straight lines at any angle. In particular, to draw parallel lines... of which the parallelogram itself is composed.