Regular polyhedrons have been the subject of interest for many great scientists. And this interest went far beyond mathematics. Plato (427 BC — 347 BC) saw them as the basis of the structure of the Universe, Kepler (1571—1630) tried to link the regular polyhedrons with the movement of the planets of the solar system (of which there) were known five at his time. Perhaps it was the beauty and harmony of the regular polyhedrons that made the great scientists of the past suggest some kind of deeper purpose for them than just geometric objects.
A regular polyhedron is a polyhedron all of whose faces are regular polygons, all of whose planar angles are equal to each other and whose dihedral angles are equal to each other. (The planar angles of a polyhedron are the angles of polygon-faces, the dihedral angles of a polyhedron are the angles between faces that have a common edge.)
Note that the convexity of a regular polyhedron follows automatically from this definition, which in some books is included in the definition.
In three-dimensional space, there are exactly five regular polyhedrons: tetrahedron, octahedron, cube (hexahedron), icosahedron, dodecahedron. The fact that there are no other regular polyhedrons was proved by Euclid (about 300 BC) in his great “Elements”.
The tetrahedron (from Greek τετρά, in compound words — four, and έδρα — facet) is a regular polyhedron with four triangular faces. It has four vertices, six edges. Since the faces of the tetrahedron are regular triangles, its planar angles are $\pi/3$. The dihedral angles of the tetrahedron are $\arccos(1/3) ≈ 70{,}53^\circ$.
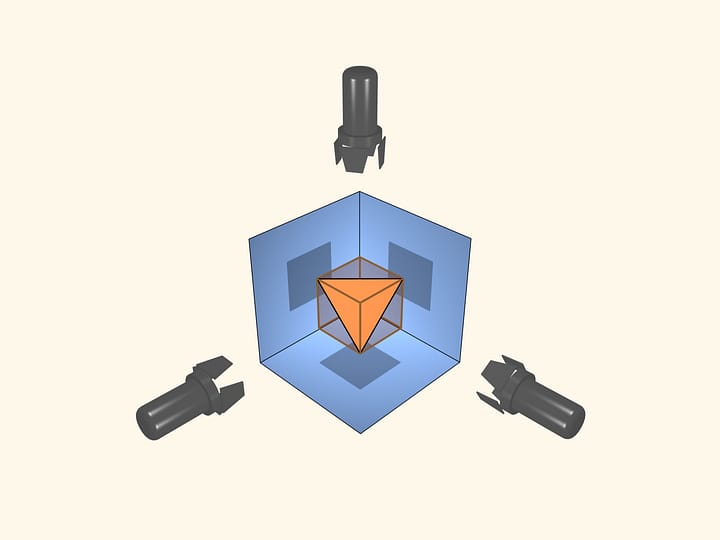
Let’s take the midpoints of the each tetrahedron face and connect them to each other with segments. These segments are equal in length and form equilateral triangles. The points are the vertices, the segments are the edges, and the triangles are the faces of another tetrahedron.
A similar construction is applicable in the more general case. Consider an arbitrary convex polyhedron and take the midpoints of its faces. Connect points of adjacent faces with segments. Thus, the points are vertices, the segments are edges and the polygons that are bounded by these segments are the faces of another convex polyhedron. This polyhedron is called dual to the original polyhedron.
As shown above, the dual to a tetrahedron is a tetrahedron.
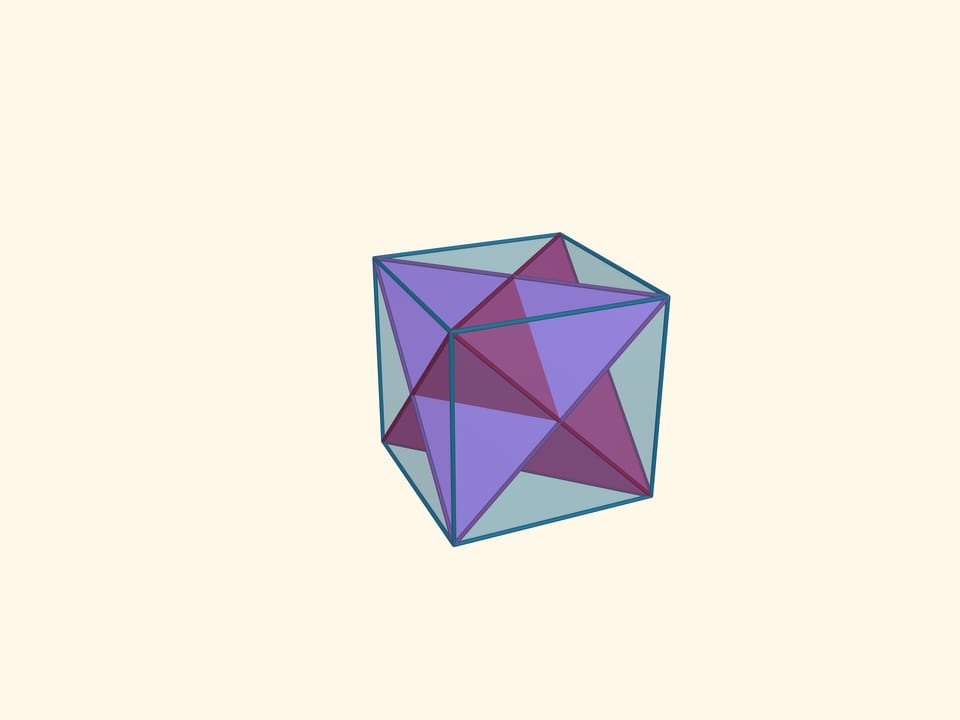
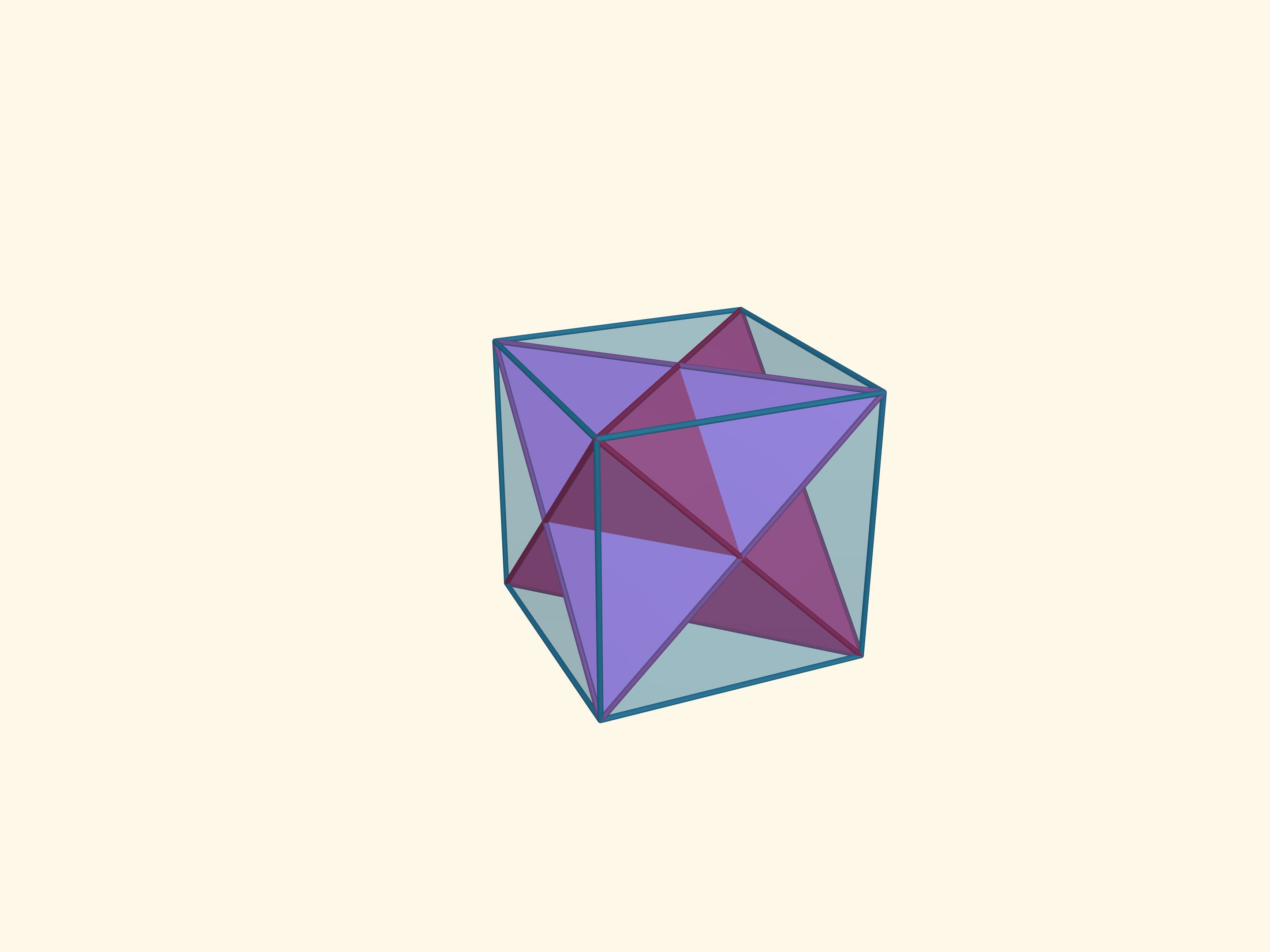
Let’s increase the size of the tetrahedron, whose vertices are the midpoints of the original tetrahedron faces, to the size of the latter. Eight vertices of such a tetrahedrons are the vertices of the cube.
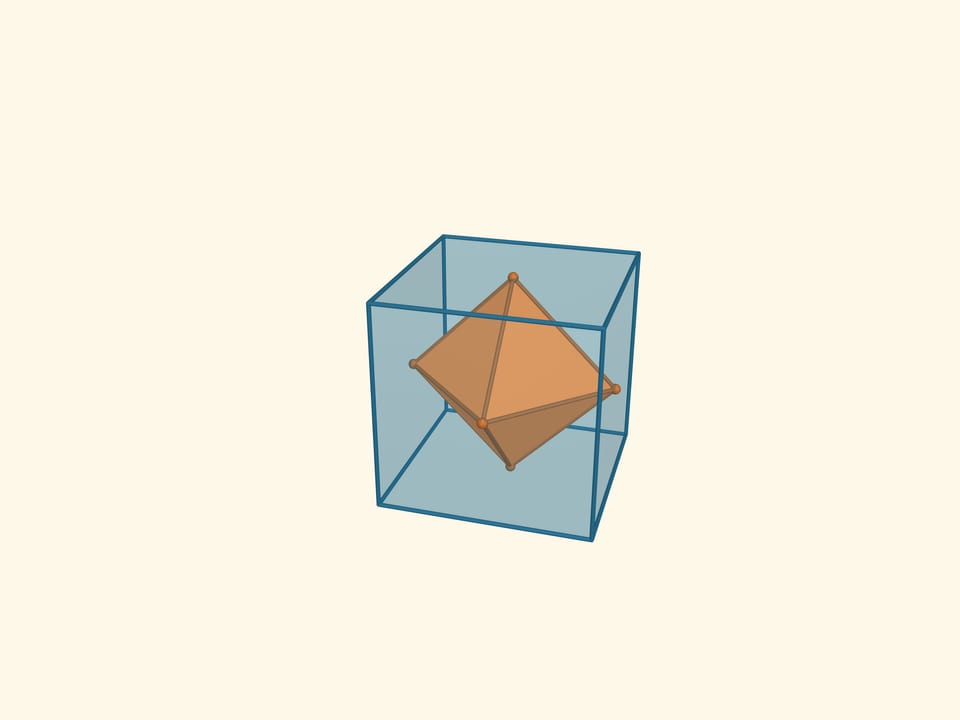
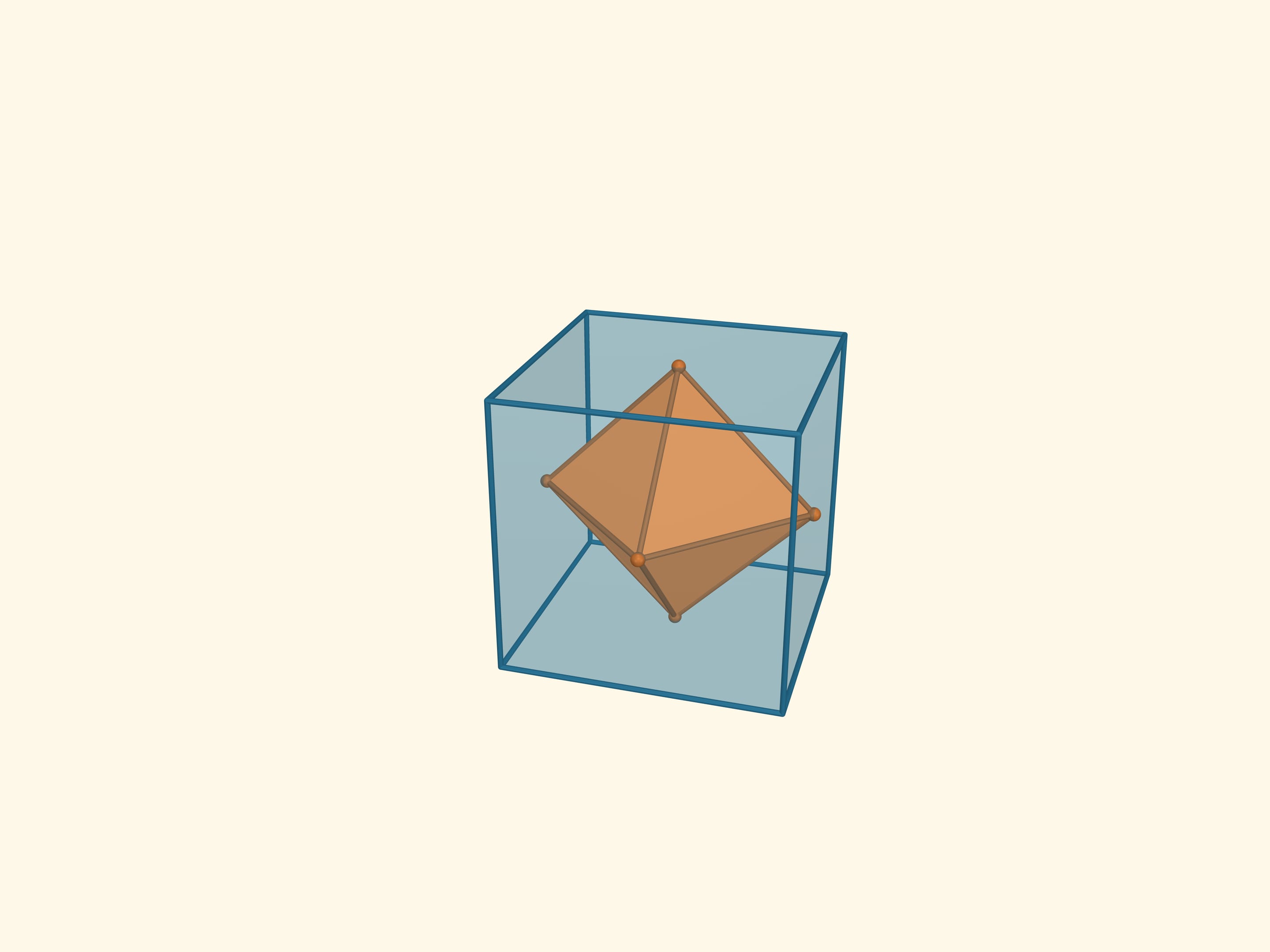
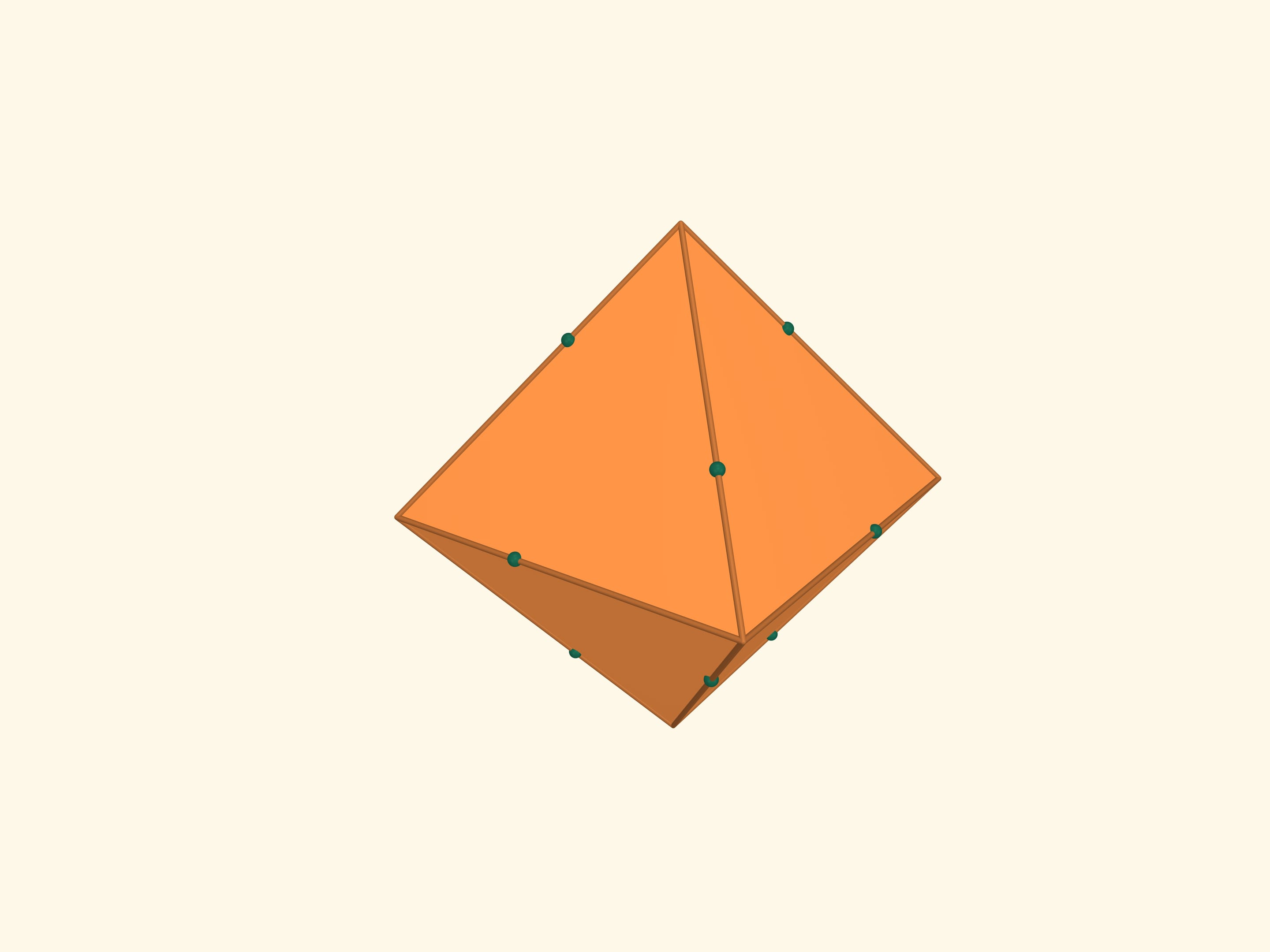
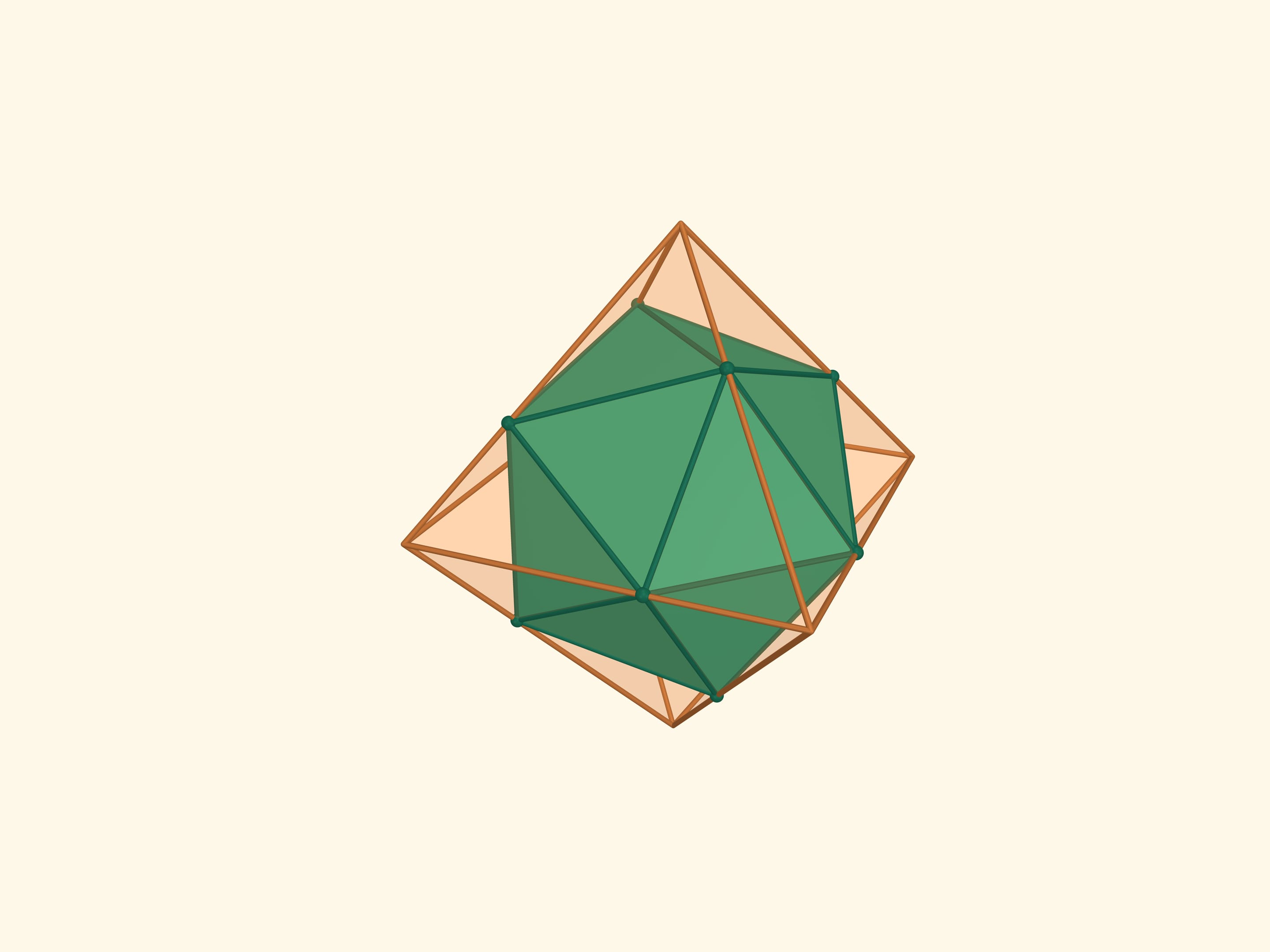
The intersection of these tetrahedrons is another regular polyhedron, the octahedron (from Greek οκτώ — eight). An octahedron has 8 triangular faces, 6 vertices and 12 edges. The flat angles of the octahedron are $\pi/3$ because its faces are right triangles, the dihedral angles are $\arccos(-1/3) ≈ 109{,}47^\circ$.
Let’s mark the midpoints of the octahedron faces and proceed to the polyhedron that is dual to the octahedron. This is a cube or hexahedron (from Greek εξά, six). A cube has edges which are squares. It has 6 faces, 8 vertices and 12 edges. The flat angles of the cube are $\pi/2$, the dihedral angles are also $\pi/2$.
If we take the midpoints of the cube faces and consider its dual polyhedron, it turns out to be an octahedron. The more general statement is correct: if we construct a dual polyhedron for a convex polyhedron and then a dual to the convex polyhedron, it will be the original polyhedron (with exact congruence).
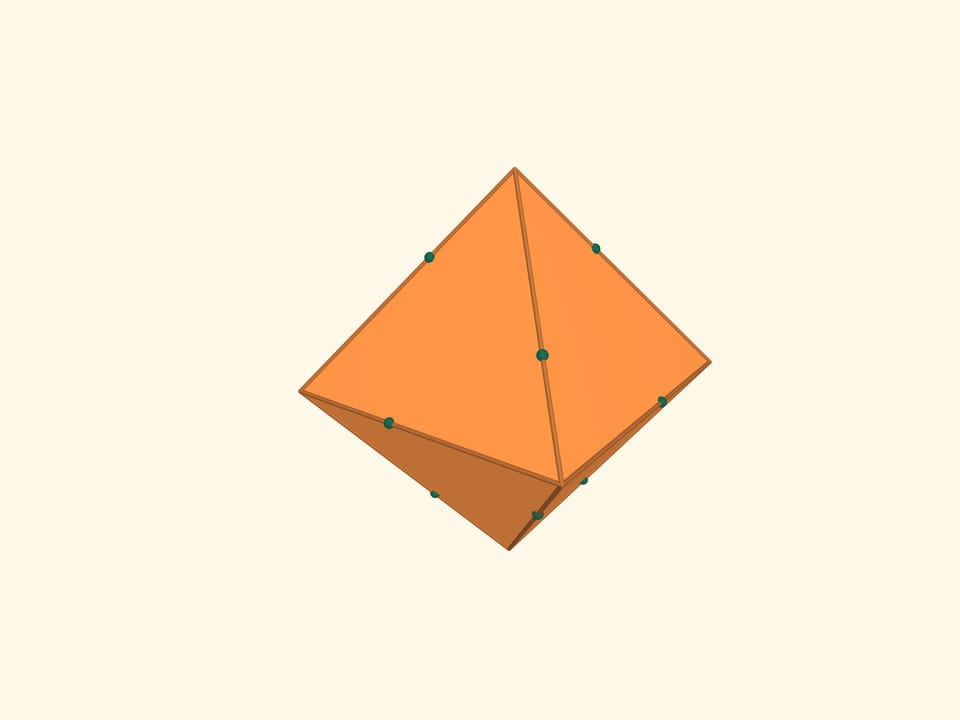
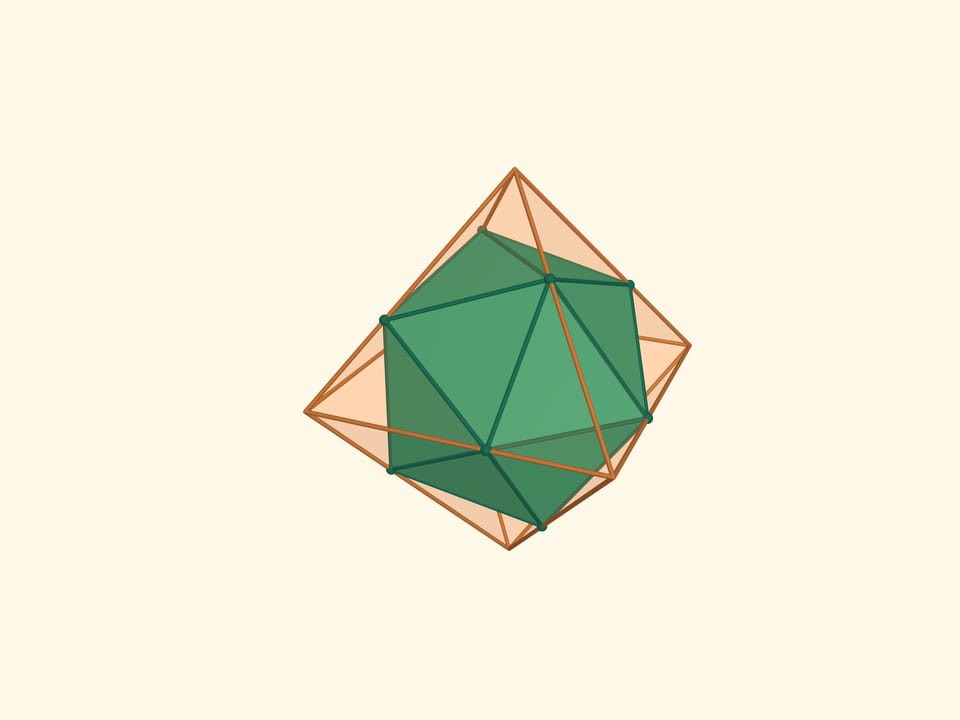
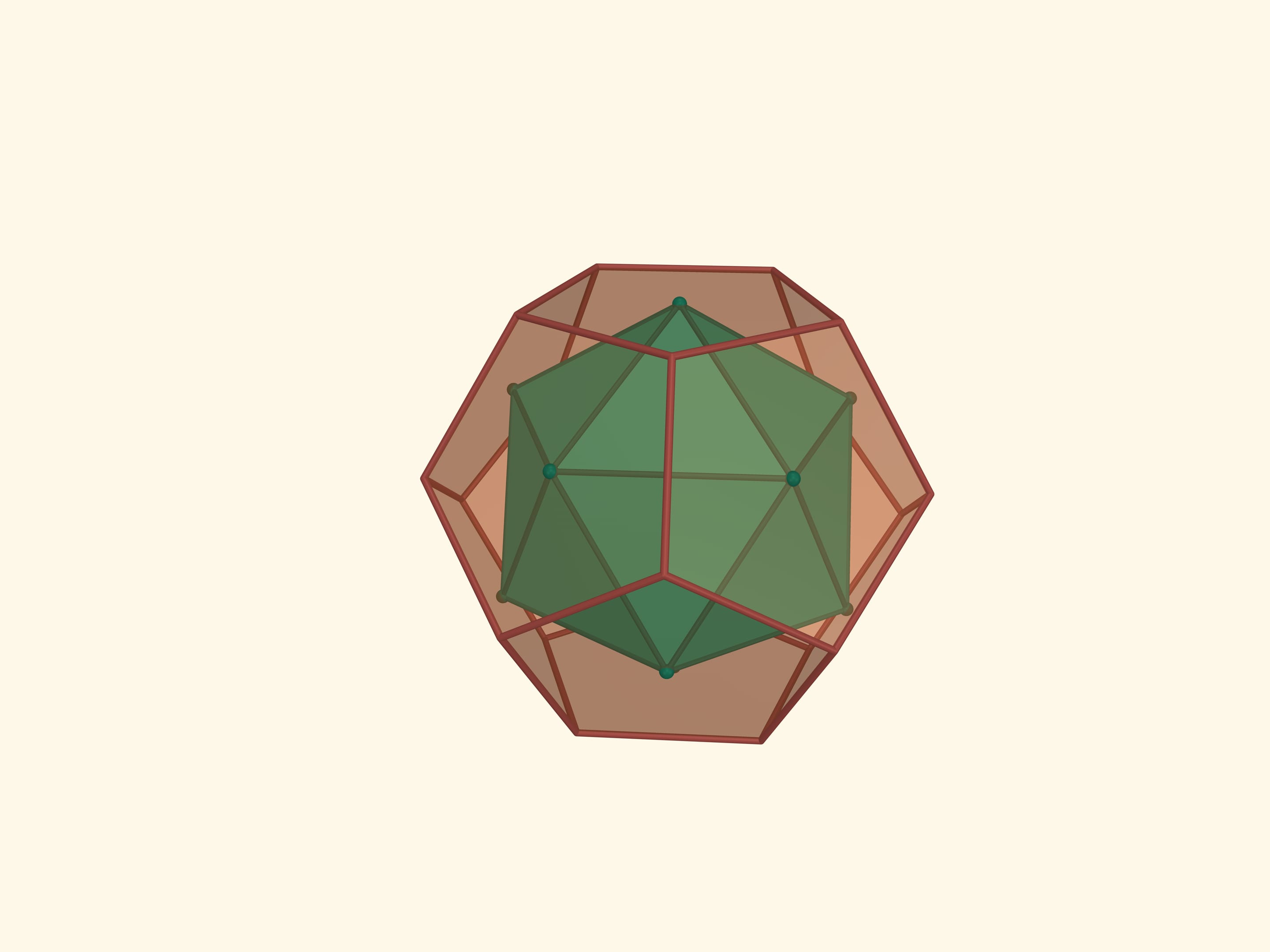
Let’s take the points on an edges of an octahedron with the condition that each edge is divided by this point in the ratio $1:(\sqrt5+1)/2$ (the Golden Section) and the points belonging to one edge are the vertices of a regular triangle. The resulting 12 points are the vertices of another regular polyhedron — icosahedron (from Greek είκοσι — twenty). An icosahedron is a regular polyhedron with 20 triangular faces. It has 12 vertices and 30 edges. The flat angles of the icosahedron are $\pi/3$, the dihedral angles are $\arccos(-1/3\cdot\sqrt5) ≈ 138{,}19^\circ$.
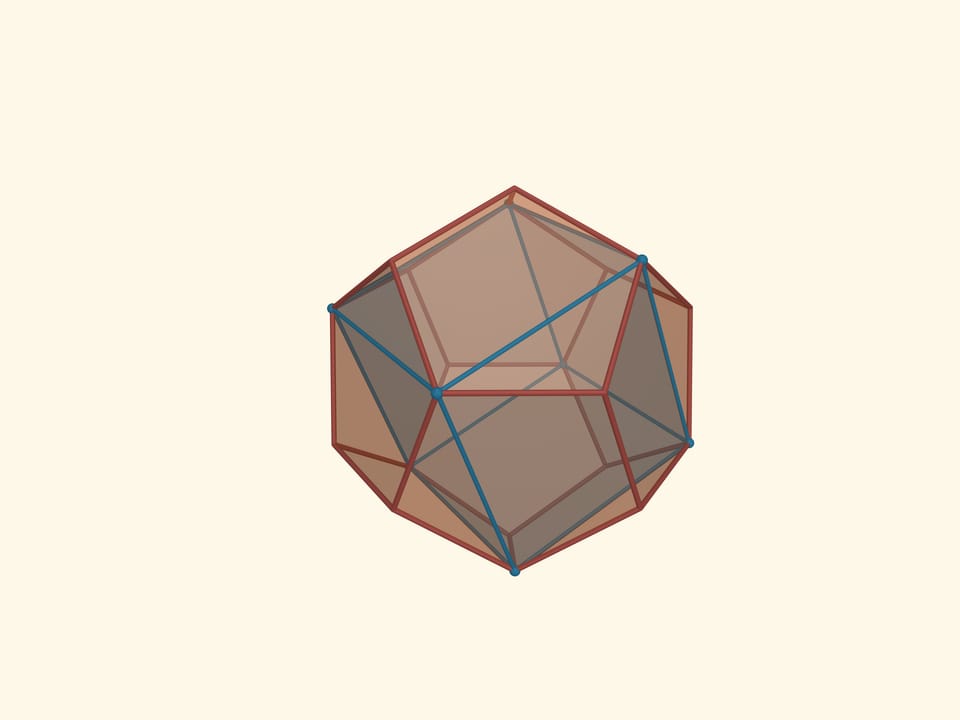
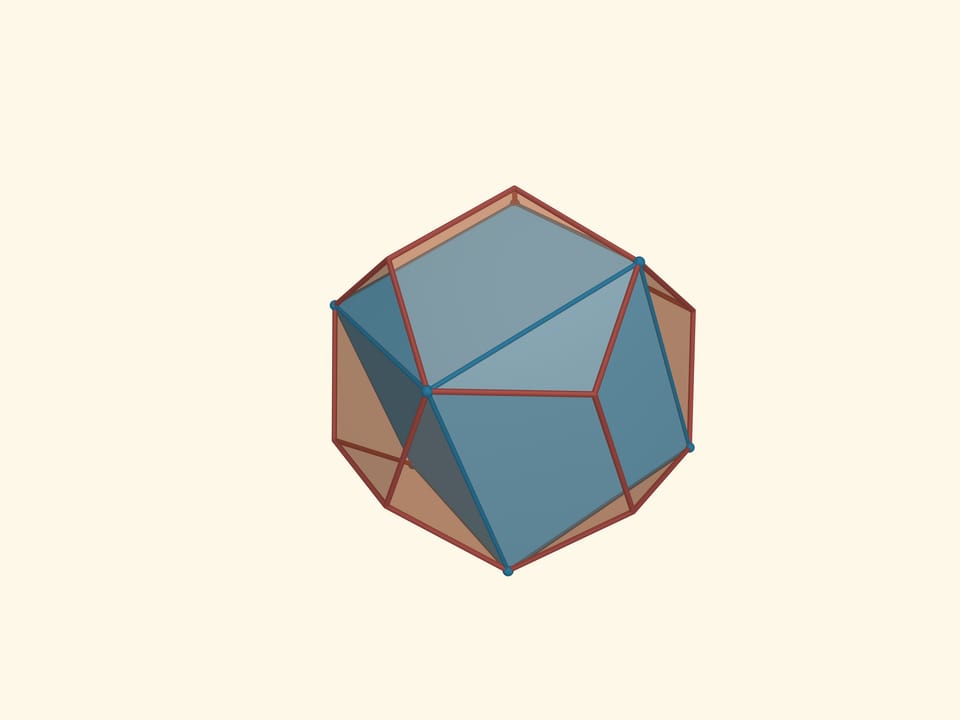
The icosahedron can be inscribed into a cube. Each face of the cube will have two vertices of the icosahedron.
Let’s rotate the icosahedron, “putting” it on a vertex, to get its more “familiar” appearance: two hats of five triangles at the south and north poles and a middle layer made of ten triangles.
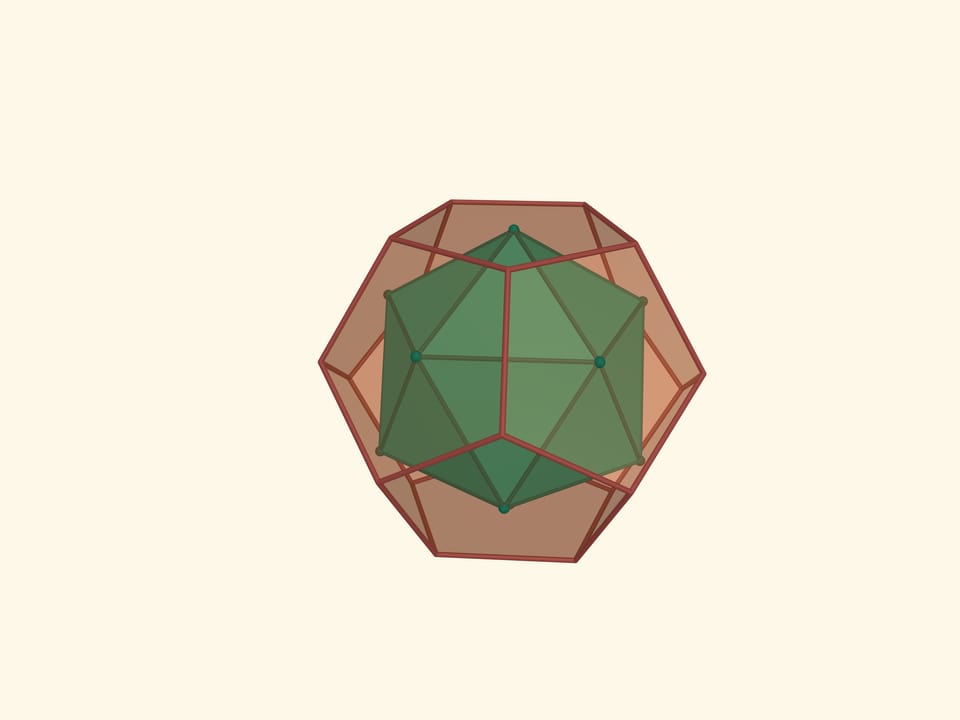
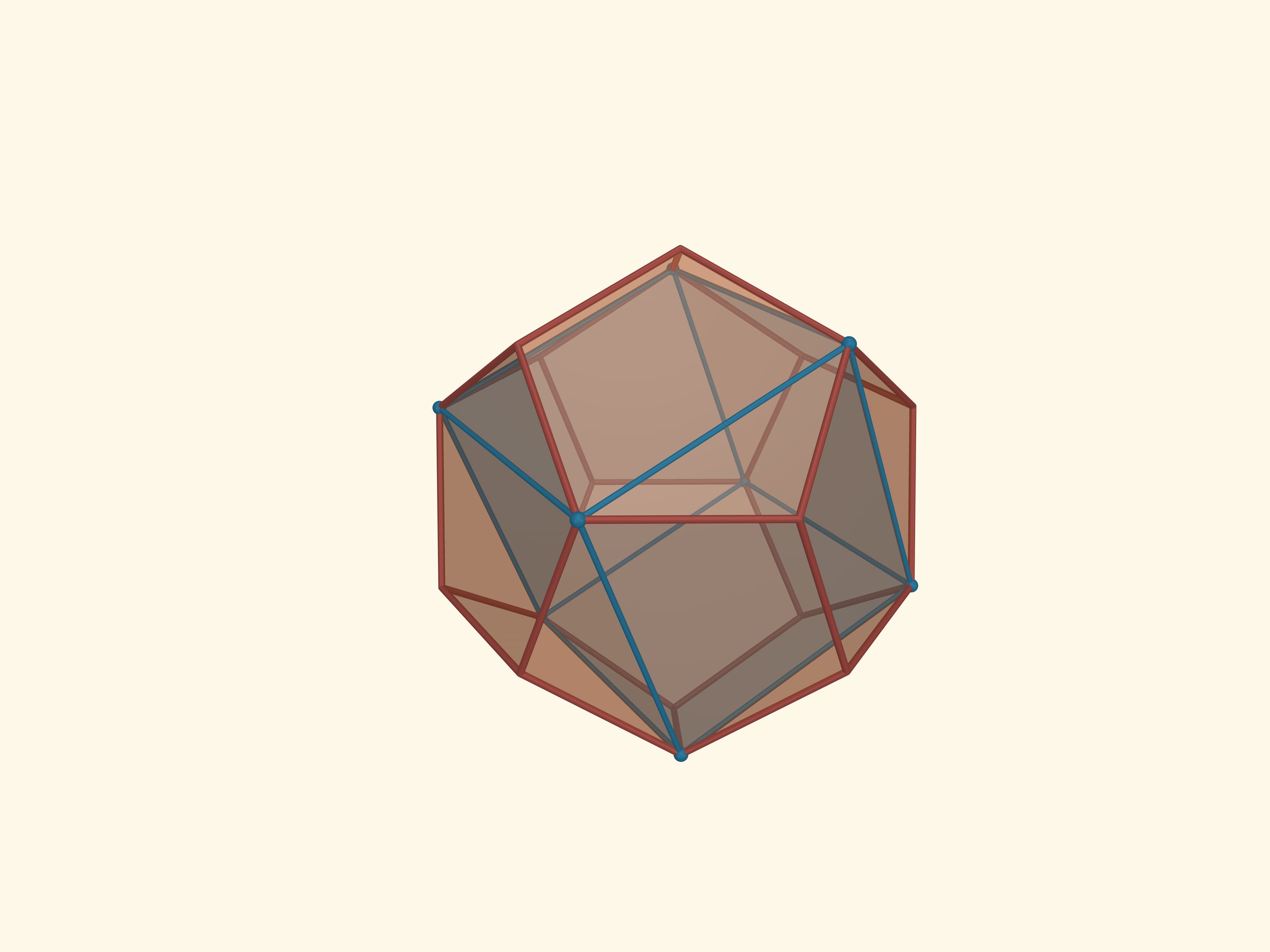
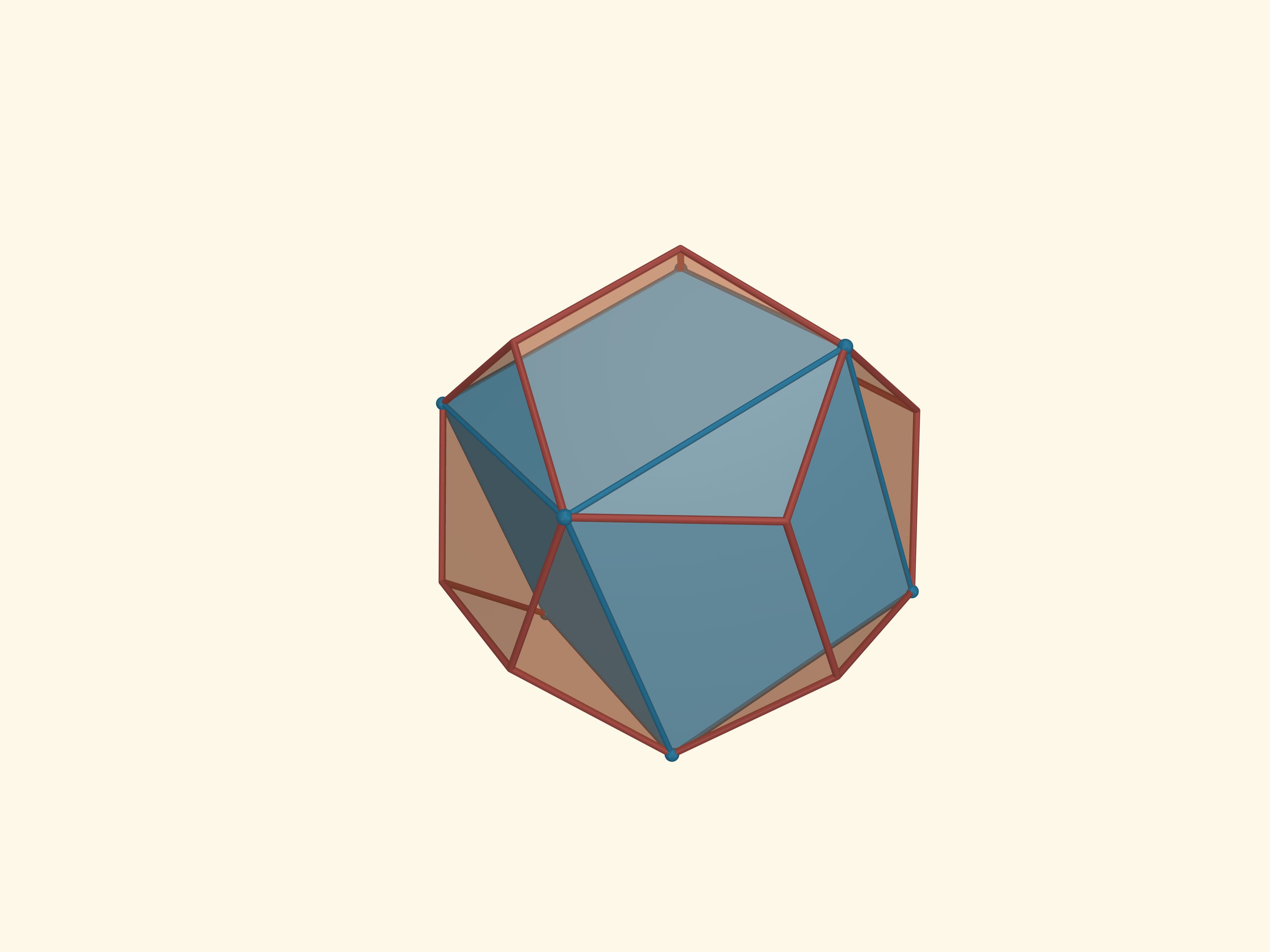
The icosahedron faces’ midpoints are the vertices of another regular polyhedron, the dodecahedron (from the Greek δώδεκα — twelve). The faces of the dodecahedron are regular pentagons. Thus its planar angles are $3\pi/5$. The dodecahedron has 12 faces, 20 vertices and 30 edges. The dihedral angles of the dodecahedron are $\arccos(-1/5\cdot\sqrt5) ≈116{,}57^\circ$.
Taking the midpoints of the decahedron faces and going to its dual polyhedron, we get the icosahedron again. So the icosahedron and the dodecahedron are dual to each other. Yet again this illustrates the fact that the dual to the dual will be the original polyhedron.
When going to a dual polyhedron, note that the vertices of the original polyhedron correspond to the faces of the dual polyhedron, the edges correspond to the edges of the dual polyhedron, and the faces correspond to vertices of the dual polyhedron. If an icosahedron has 20 faces then its dodecahedron has 20 vertices, and they have the same number of edges, If a cube has 8 vertices then its dual octahedron has 8 faces.
There are different methods for regular polyhedrons to be inscribed into each other, which lead to many remarkable constructions. Interesting and beautiful polyhedrons are also obtained by combining and intersecting them.
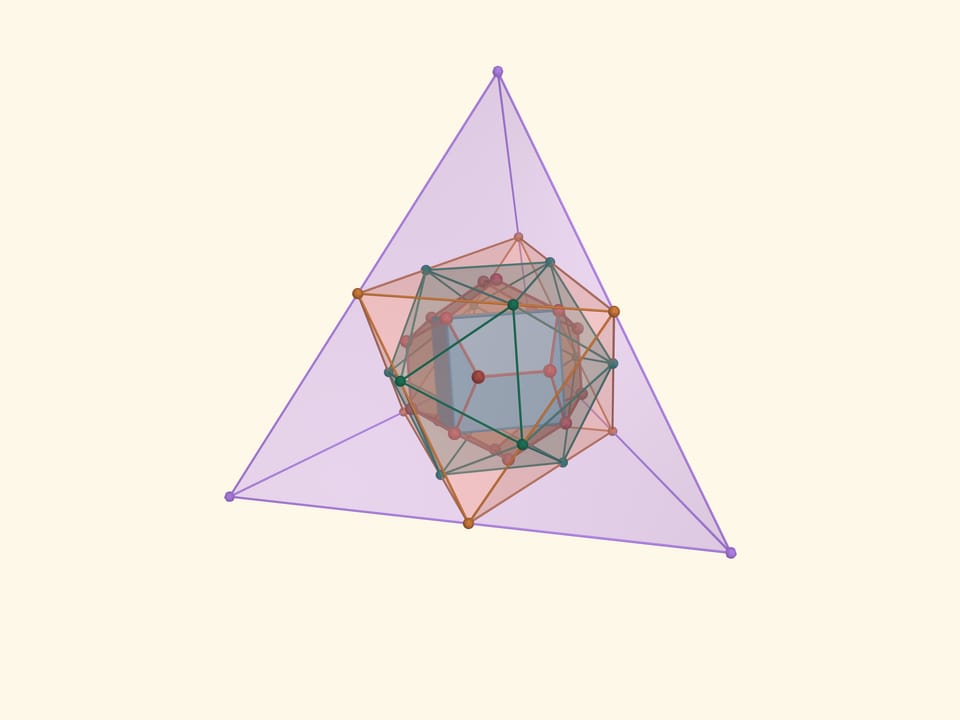
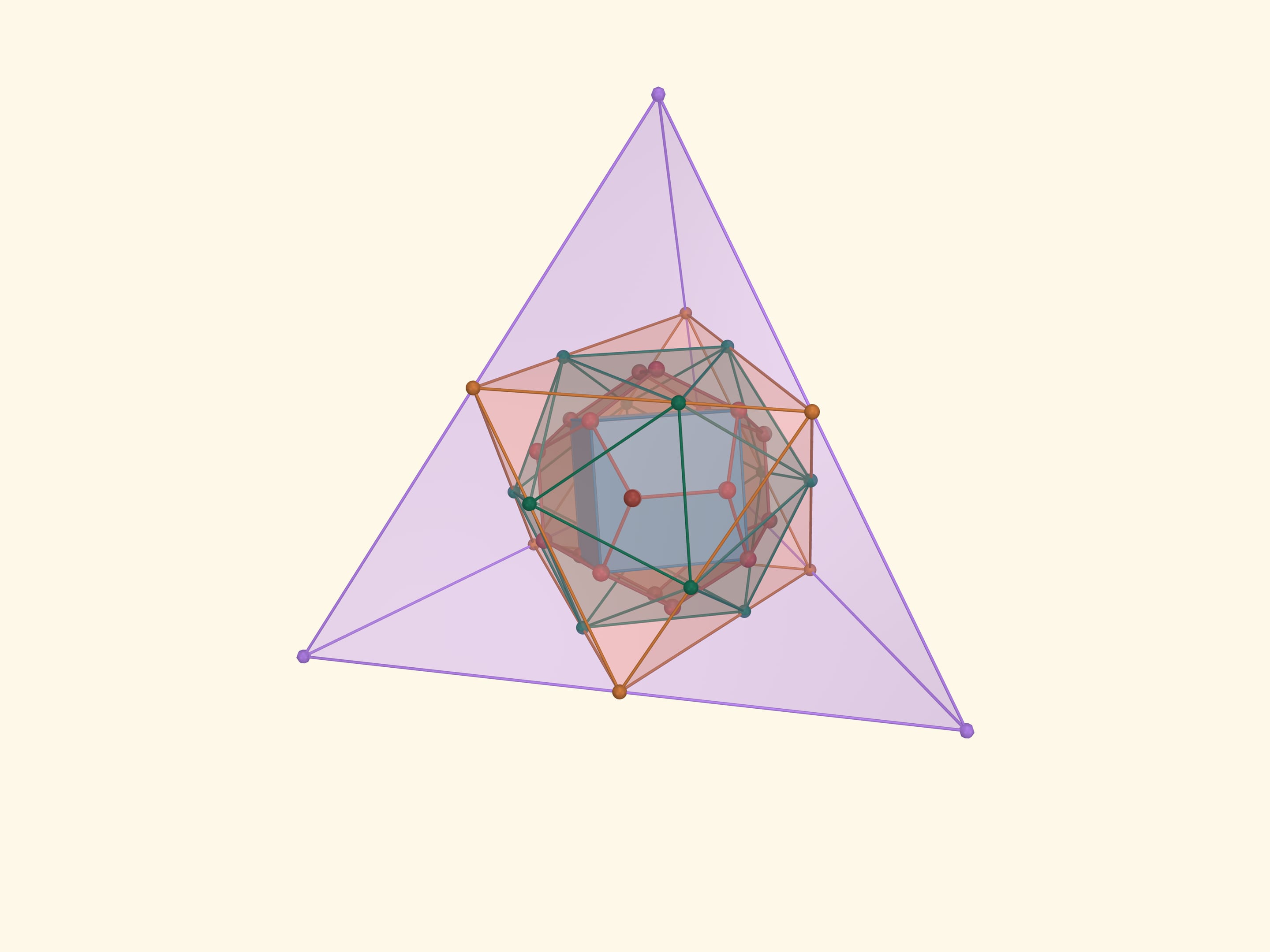
In a dodecahedron, we inscribe a cube so that all 8 vertices of the cube coincide with vertices of the dodecahedron. Then we circumscribe the icosahedron around the dodecahedron so that its vertices are in the midpoints of the icosahedron edges. Then circumscribe an octahedron around the icosahedron so that the vertices of the icosahedron rest on the edges of the octahedron. Finally, circumcircle the octahedron around the tetrahedron so that the vertices of the octahedron rest on the midpoints of the tetrahedron edges.
This construction was made from pieces of broken wooden ski sticks by the great mathematician of the 20th century, V. Arnold, in his childhood. Vladimir Igorevich kept it for many years, and then gifted it to the laboratory for popularization and propaganda of mathematics at the Steklov Mathematical Institute.