There is a whole variety of nets for the most usual polyhedra. But is it really possible to fold a regular tetrahedron of this sheet of cardboard?
Unfold the tetrahedron into a traditional net.
Draw a segment connecting a vertex of the the big triangle and the center of the opposite side (which is a vertex of the initial tetrahedron) and cut the cardboard along this segment. Turn a part of the net around the point that represents the vertex of the tetrahedron. Doing that we'll glue two edges, but in the initial tetrahedron they were glued in the same way, so we didn't break the gluing conditions. Now we have an additional part of the border that we'll mark as red.
Let's repeat this operation.
Once again, draw a segment from the corner to the center of the opposite side and Turn and glue. We get the same sheet of cardboard we saw in the beginning of the movie!
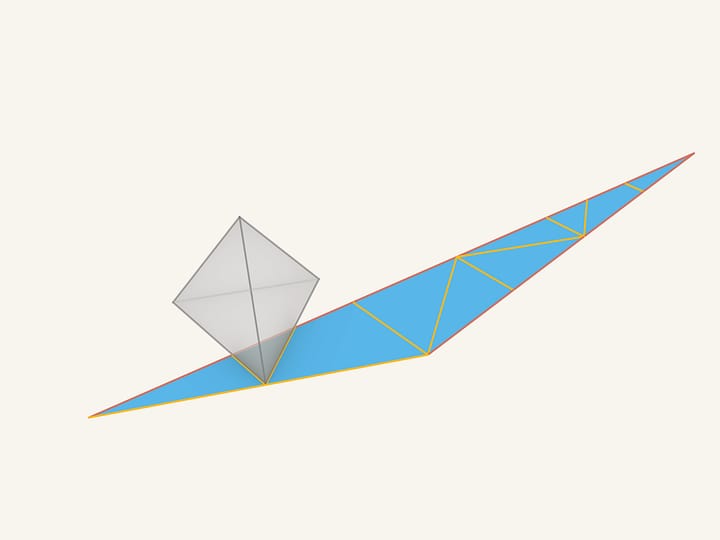
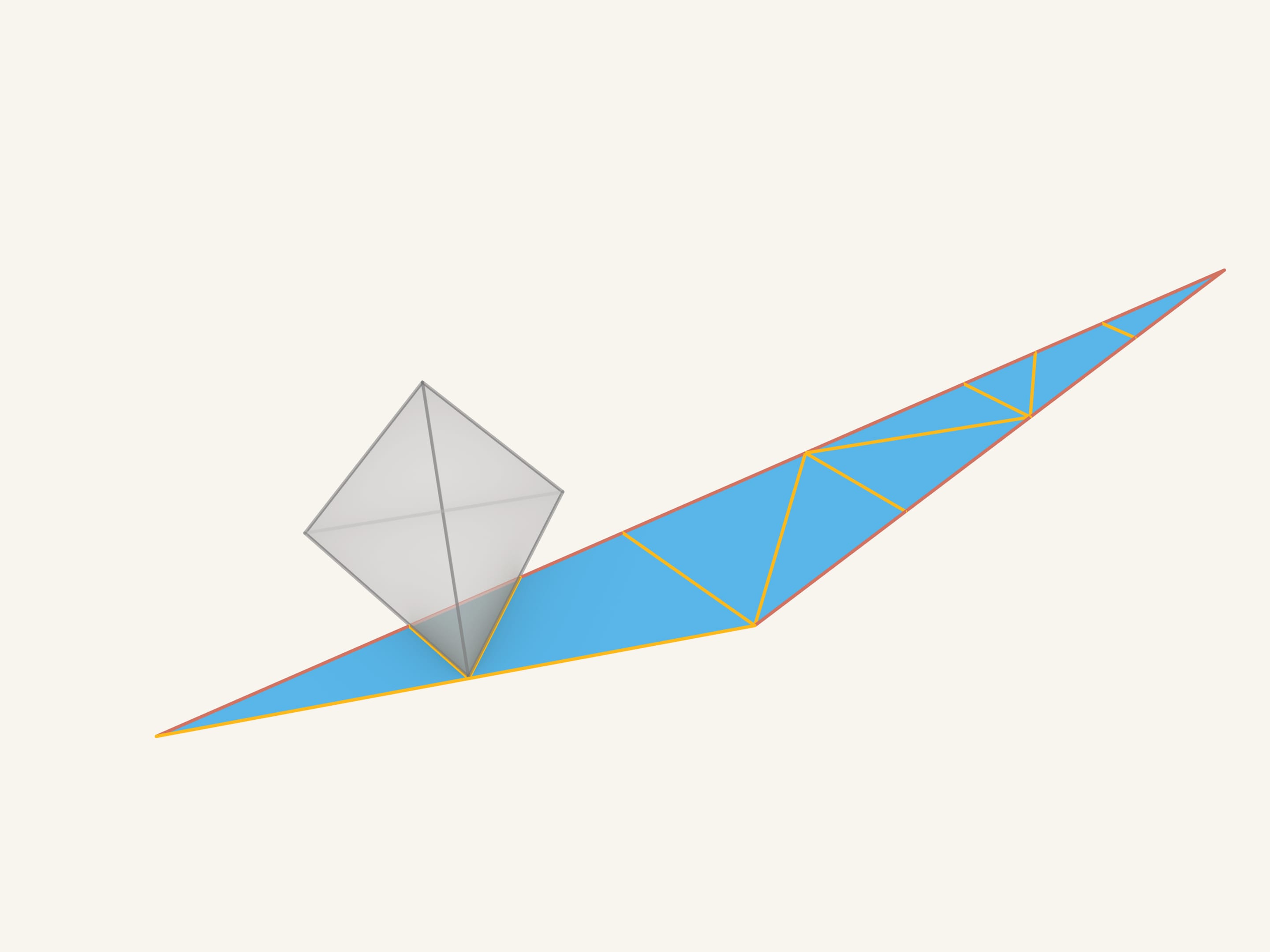
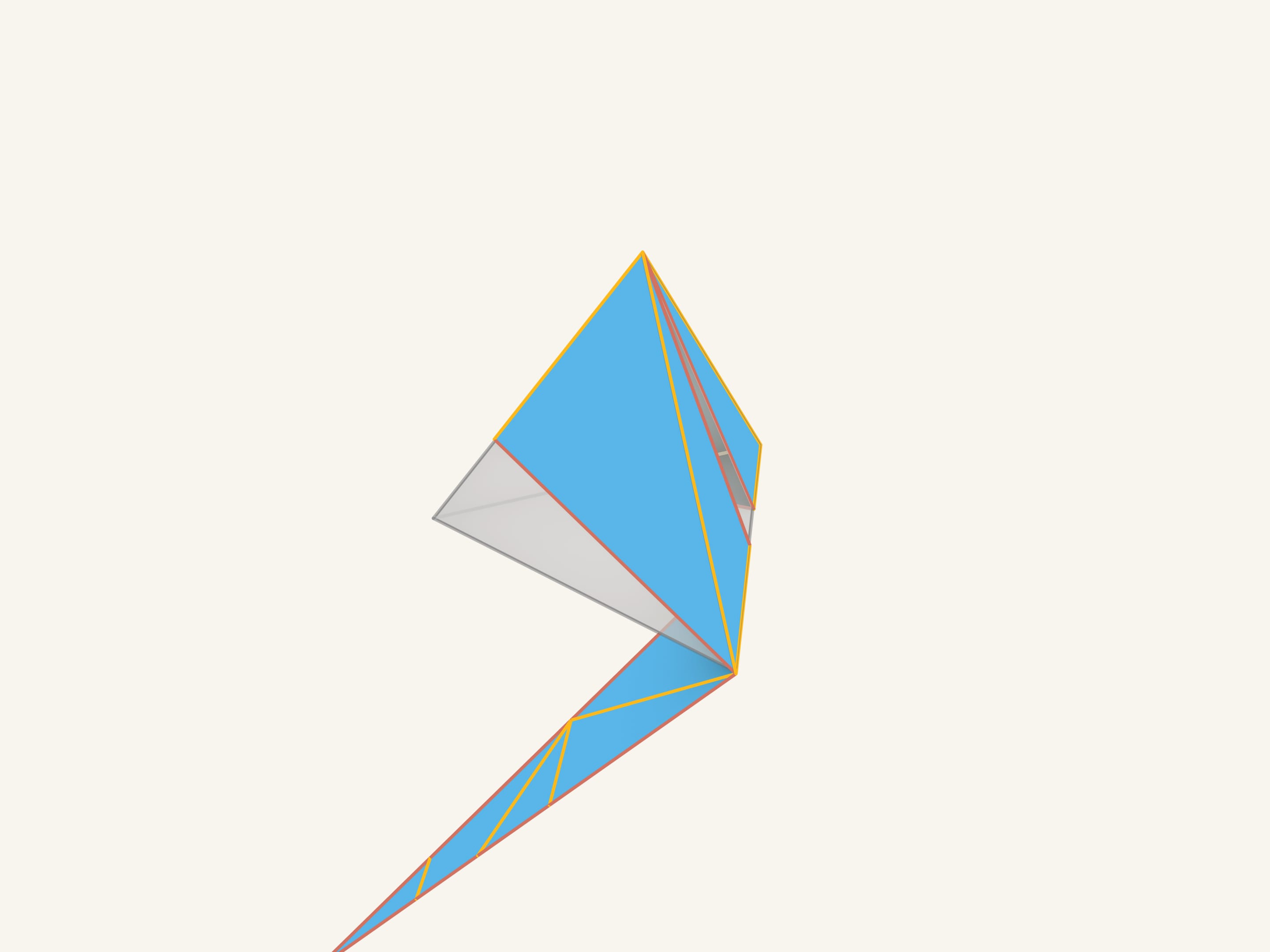
Let's make sure that the resulting sheet of cardboard is a net of the initial polyhedron. In the left upper part of the triangle there are pieces that remain unmoved from the beginning. One of the small triangles corresponds to a part of the initial tetrahedron's base. Let's match them.
And now we'll wind the figure round the tetrahedron. As we see, everything matches!
All the segments of the red «false» edges connect the triangles that lie in the same plane, that means that after gluing they will disappear. Those segments that were painted in yellow lie on the edges of the tetrahedron and are the real edges.
The question whether one can fold a convex polyhedron out of the given sheet of cardboard is answered by a theorem of a great Russian mathematician Alexander Danilivich Alexandrov. It is possible to figure out where the future vertices are. But we still don't know how will the real edges go from vertex to vertex. But it is another story for another movie…
Other etudes in “Polyhedra’s inner geometry”
