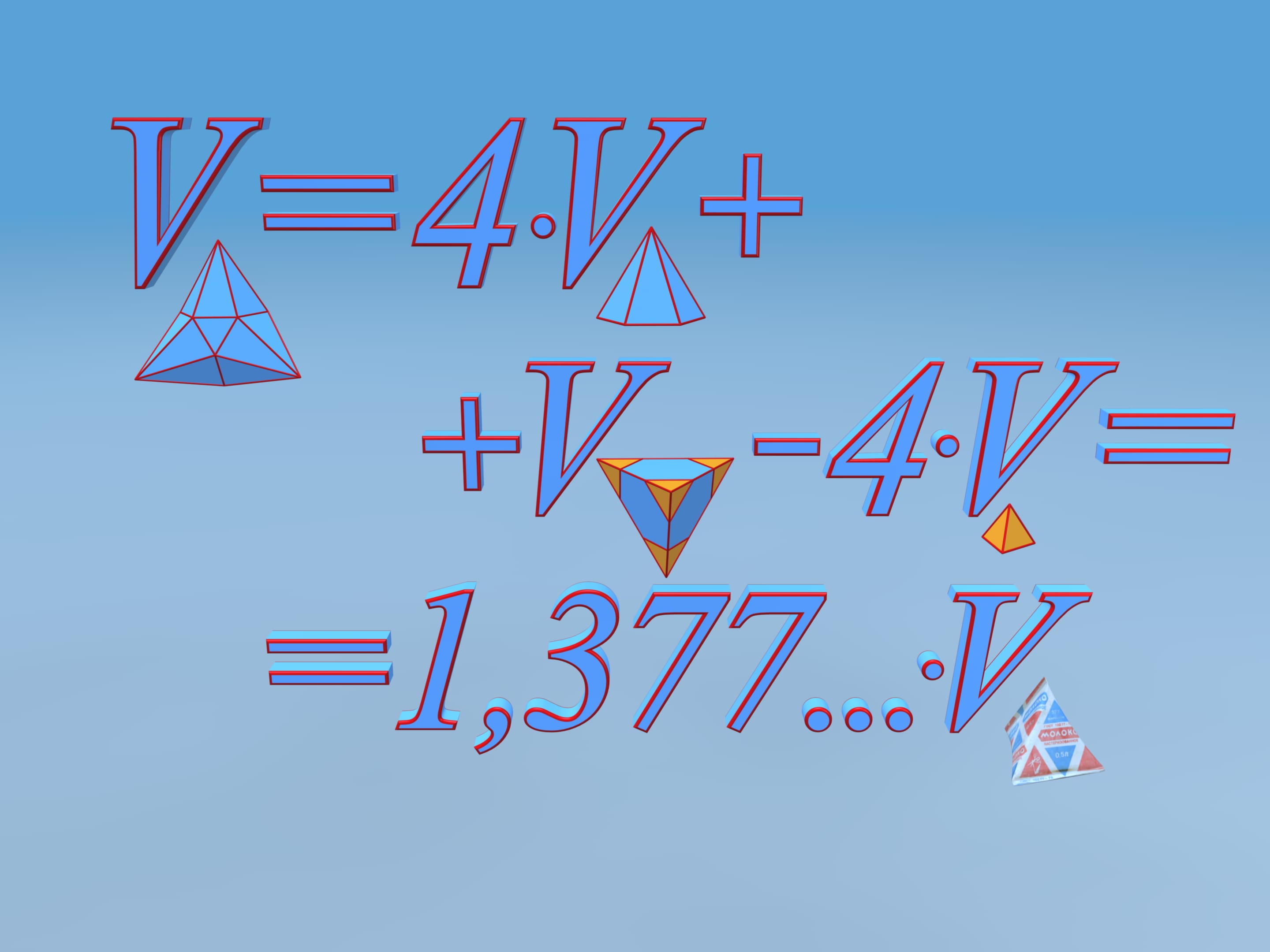Can you remember how a milk package looked like in Soviet times? Surprisingly, few people remember what was drawn on it, though the whole country bought them almost every day for over than 20 years.
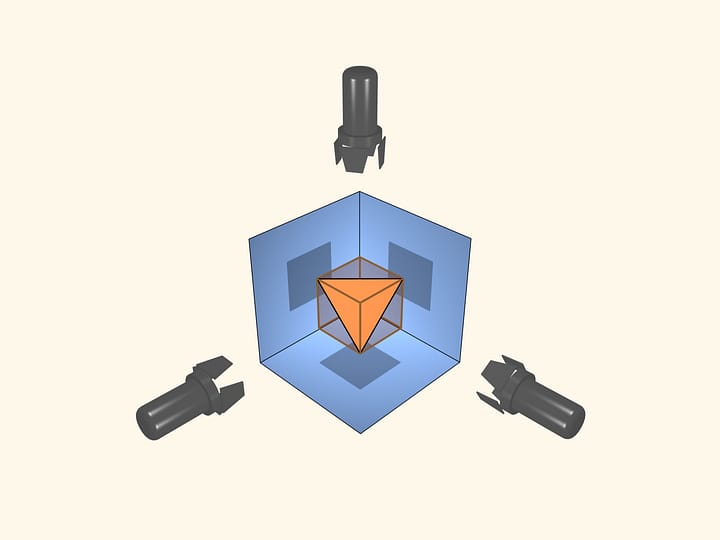
Anyway, everyone remembers that milk package was tetrahedral (in the form of regular triangular pyramid). These packages were invented by Tetra Pak in the 1940s. In those days Tetra Pak brought two innovations. First, it started to pour out edible liquids into pasteboard packages. Second, the production of tetrahedral packages was so easy that it became possible to manufacture them right at the milk plants.
The most common milk package in the Soviet Union looked like this.
Is it possible to fold a piece of pasteboard of which a milk package is made into a package of greater volume?
Mathematically saying, is it possible to fold a development of a tetrahedron into a polyhedron with a greater volume?
A theorem of A. Aleksandrov sais that it's not possible to fold it into a convex polyhedron with greater volume. However, we may be able to make a nonconvex polyhedron with greater volume.
Surprisingly as it may seem, it is possible!
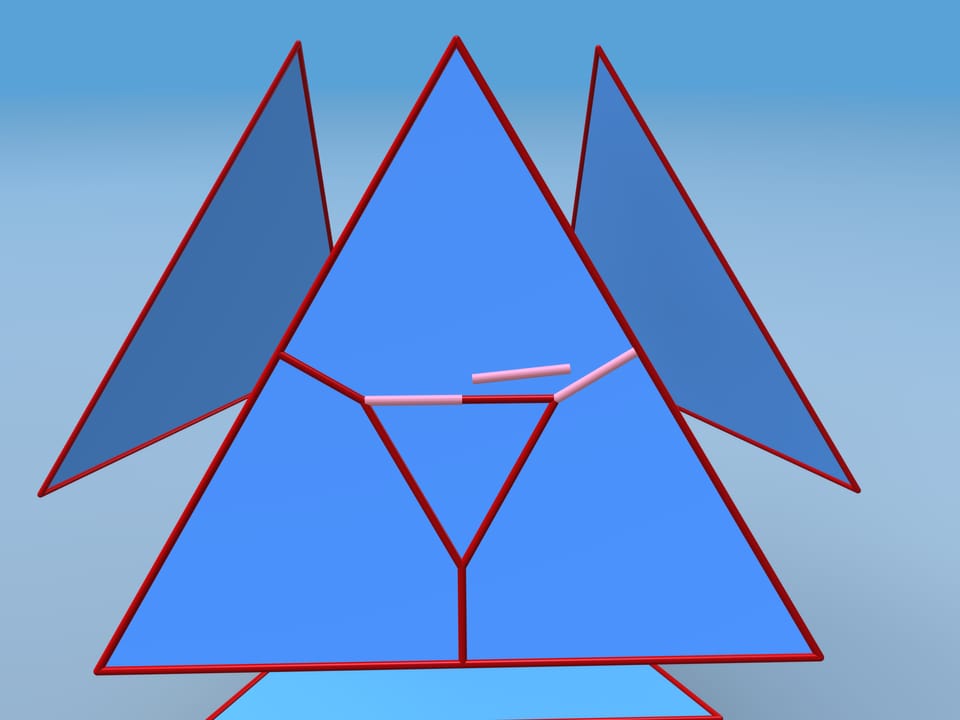
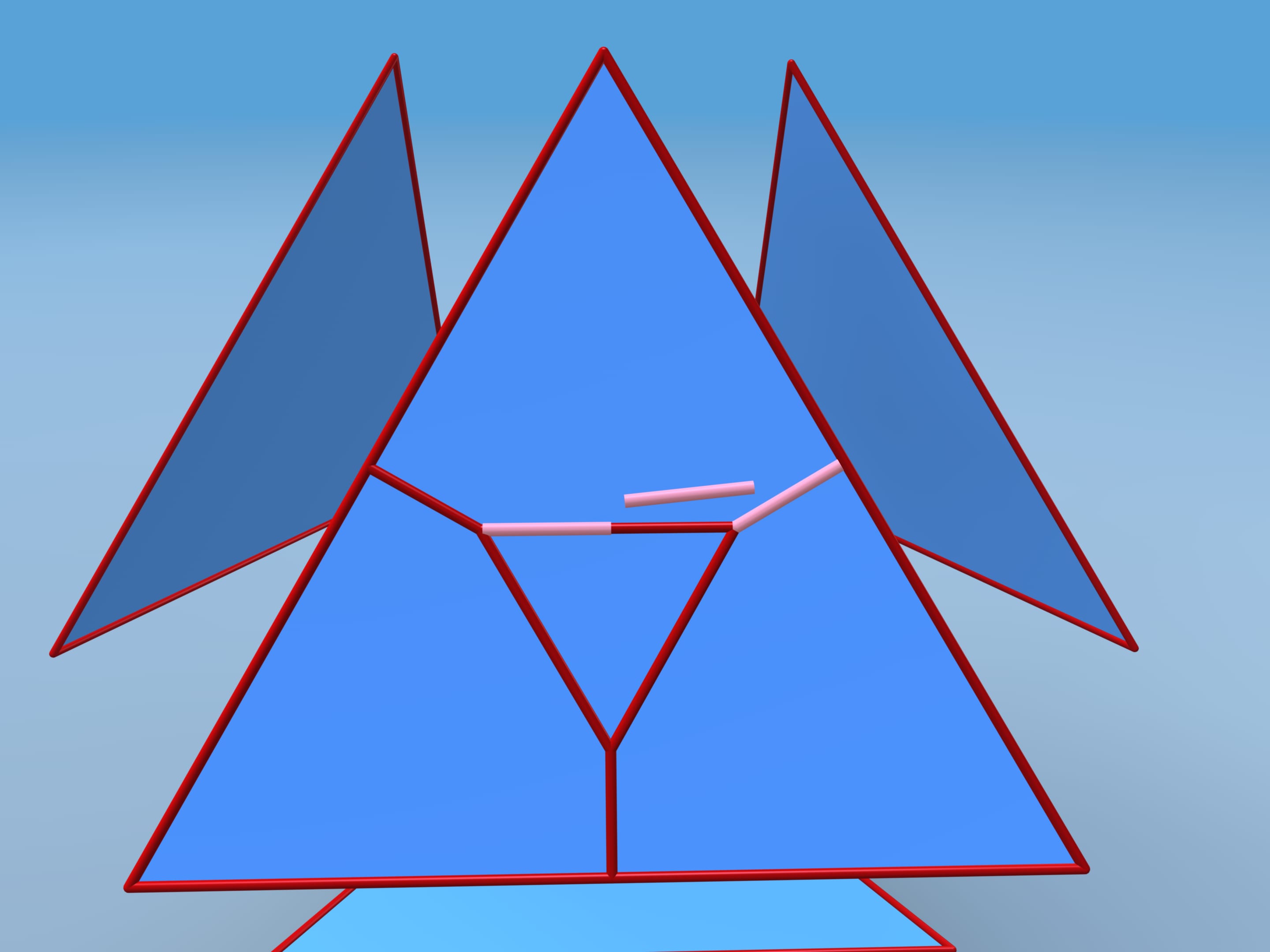
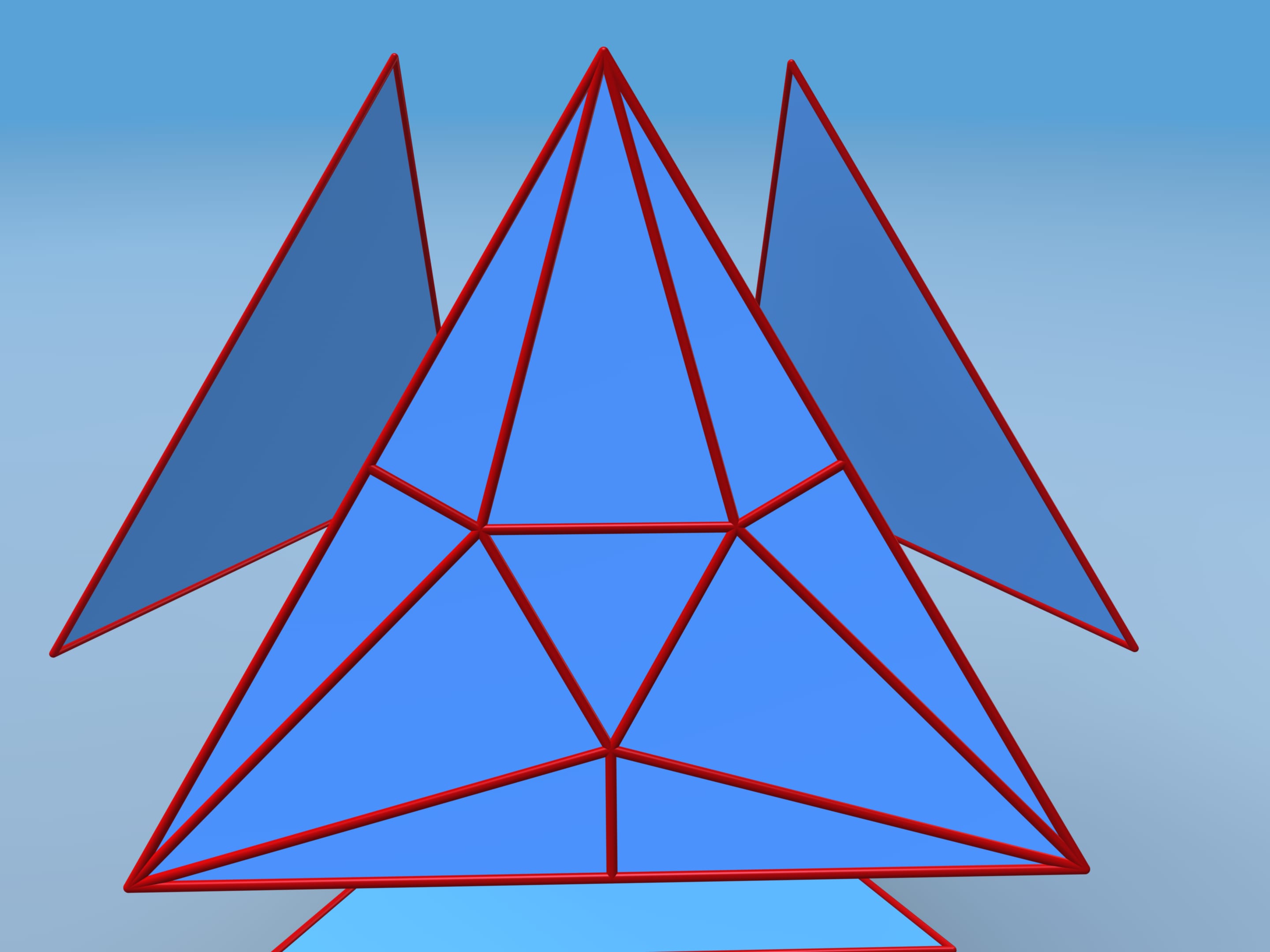
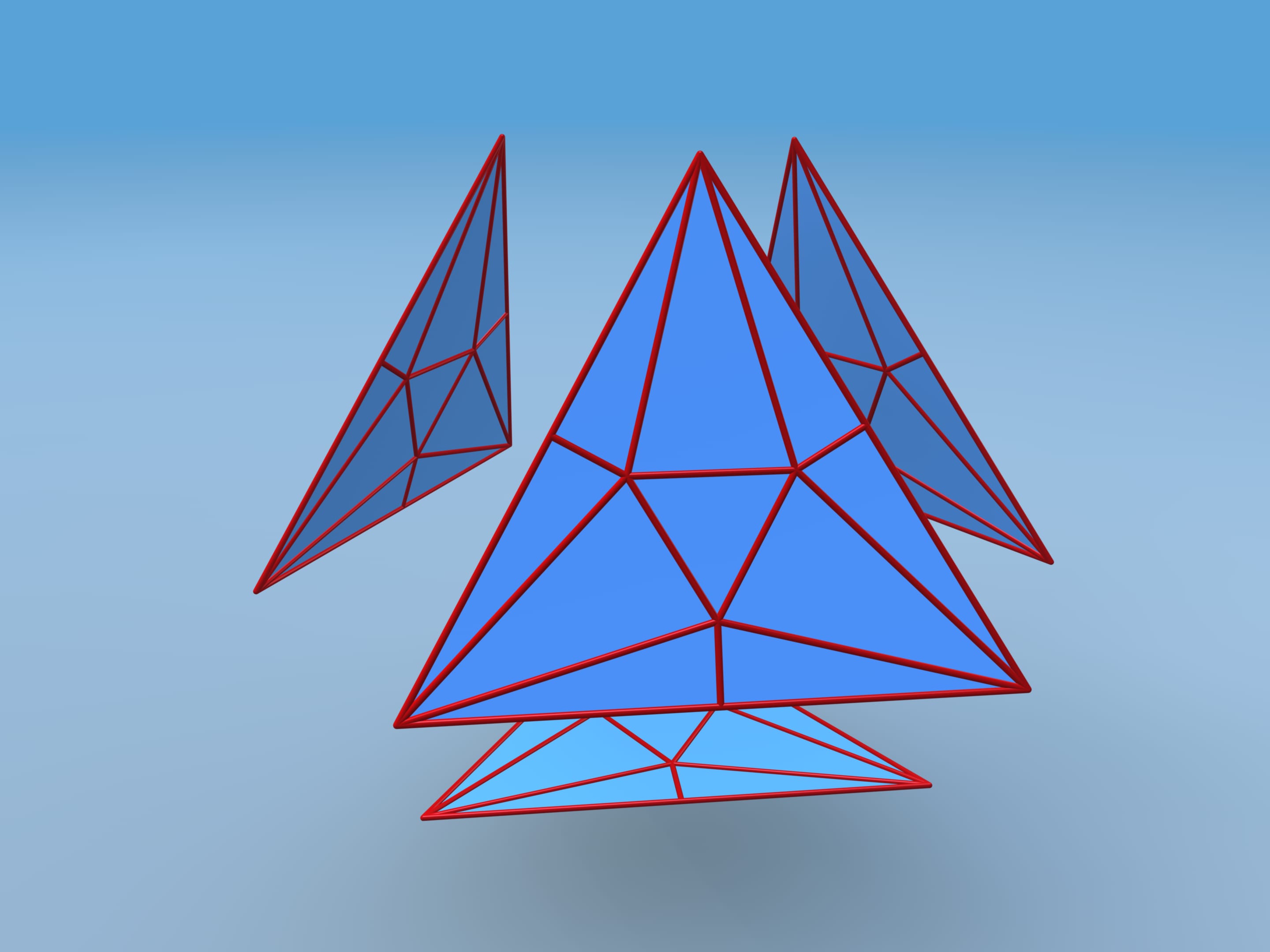
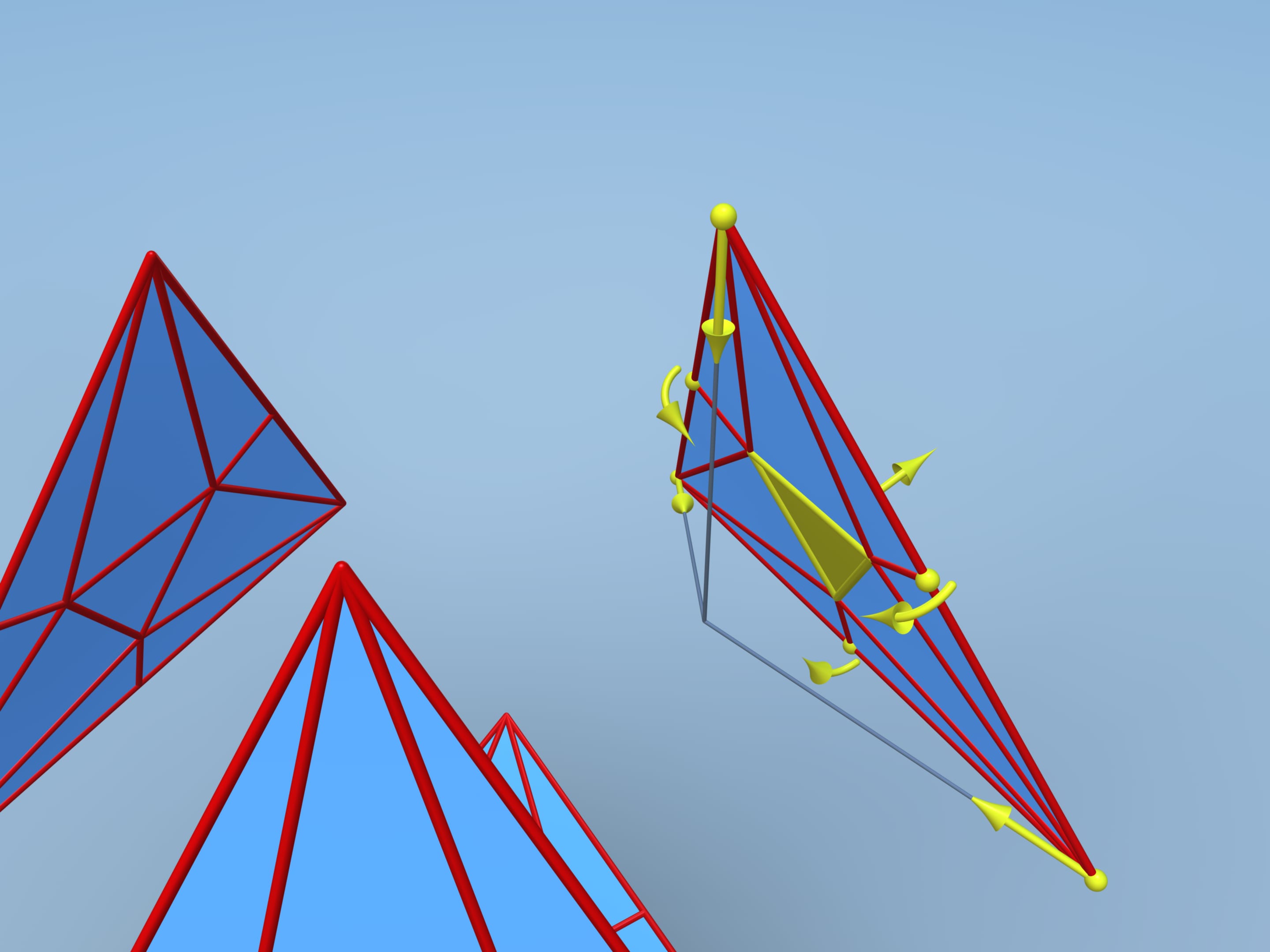
Let us follow David D. Bleecker's construction, suggested in 1996. Move faces apart and add vertices and edges on each face. Consider the central regular triangle with side length additional edges.
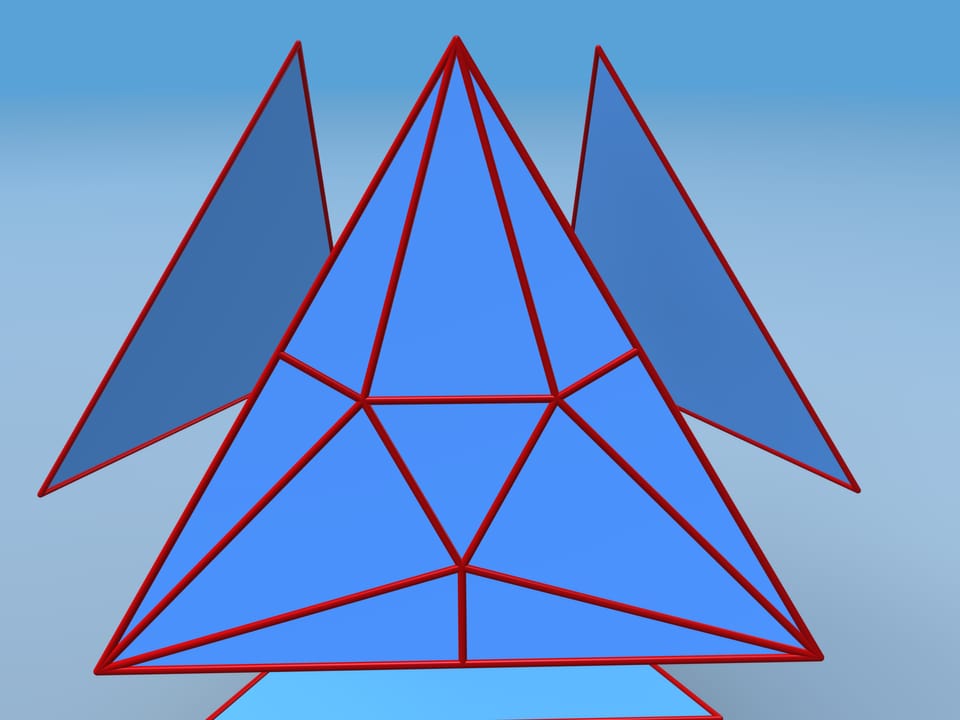
Repeat the coplanar and the edges between them disappear.
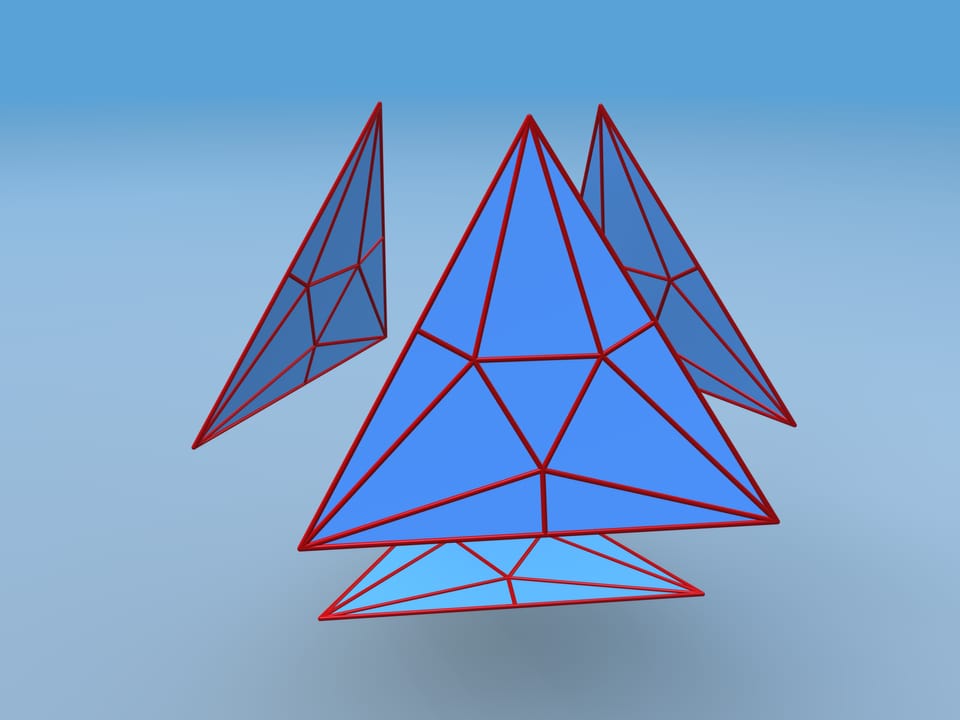
Let's calculate the volume of this polyhedron. We shall divide it into pieces. Our polyhedron consists of 4 equal hexagonal pyramids and truncated tetrahedra. To simplify the calculation, attach small tetrahedra to our tetrahedron and then subtract their volume away the whole volume.
It turns out that the volume of the constructed polyhedron is 37.7% greater than that of the initial one. Hence, a piece of paper from which tetrahedral packages were made can be folded into a package over a third more capacious!
Surprisingly, this tetrahedron is not an exception. It turns out that a development of any convex polyhedron with triangular faces can be folded into a polyhedron with greater volume. This theorem was proved by D.Bleeker in 1996. He proposed an algorithm to do it.
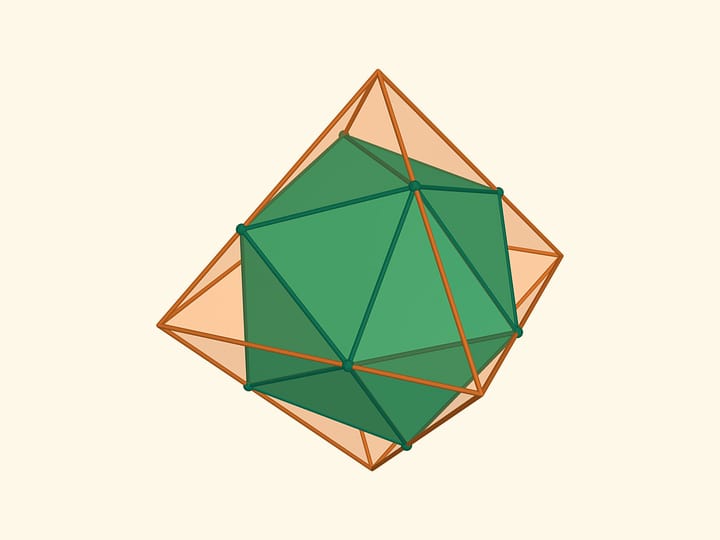
In his article D. Bleecker considered, besides polyhedrons with triangular faces, two polyhedra that do not belong to this class: the cube and the dodecahedron. Their developments can also be folded into nonconvex polyhedrons which enclose more volume than the initial ones.
Hypothesis
Development of any convex polyhedron can be folded into a nonconvex polyhedron with greater volume.
Open problem
Prove (or disprove) the hypothesis.