Sun. Rain. Rainbow.
Scientists of different times have tried to explain this natural phenomenon. A complete theory of the rainbow goes beyond geometric and even wave optics and requires a powerful mathematical apparatus. The film gives the first insight into the rainbow, which is nevertheless remarkable and by no means simple. This insight is based on the work of René Descartes and Isaac Newton.
René Descartes had explained the geometry of the rainbow: its shape and location in the sky. Isaac Newton “colored” the rainbow by explaining its colors.
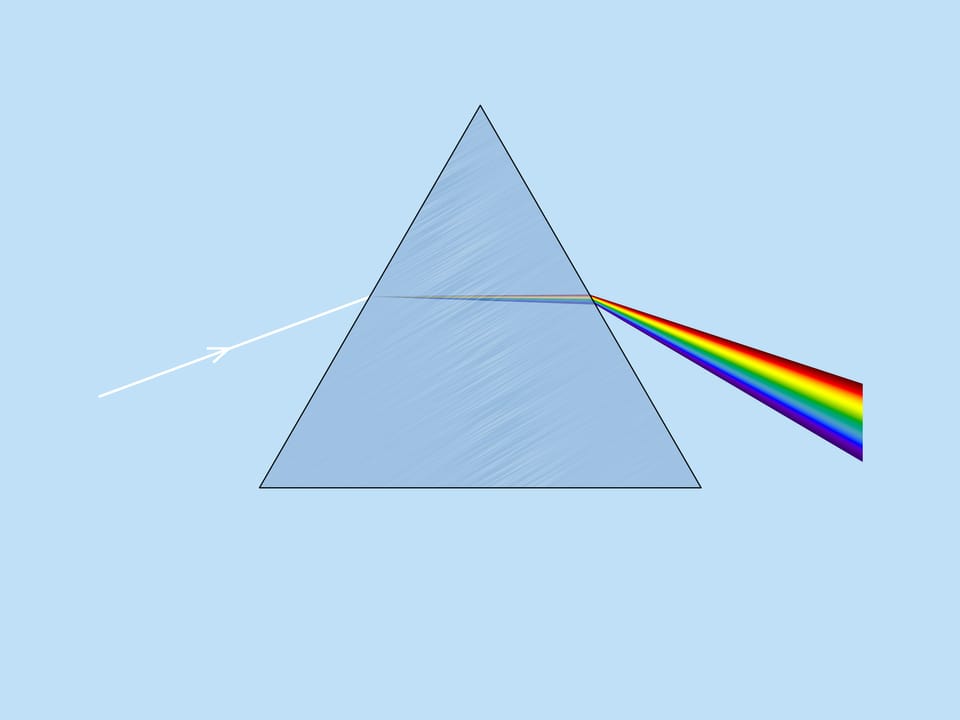
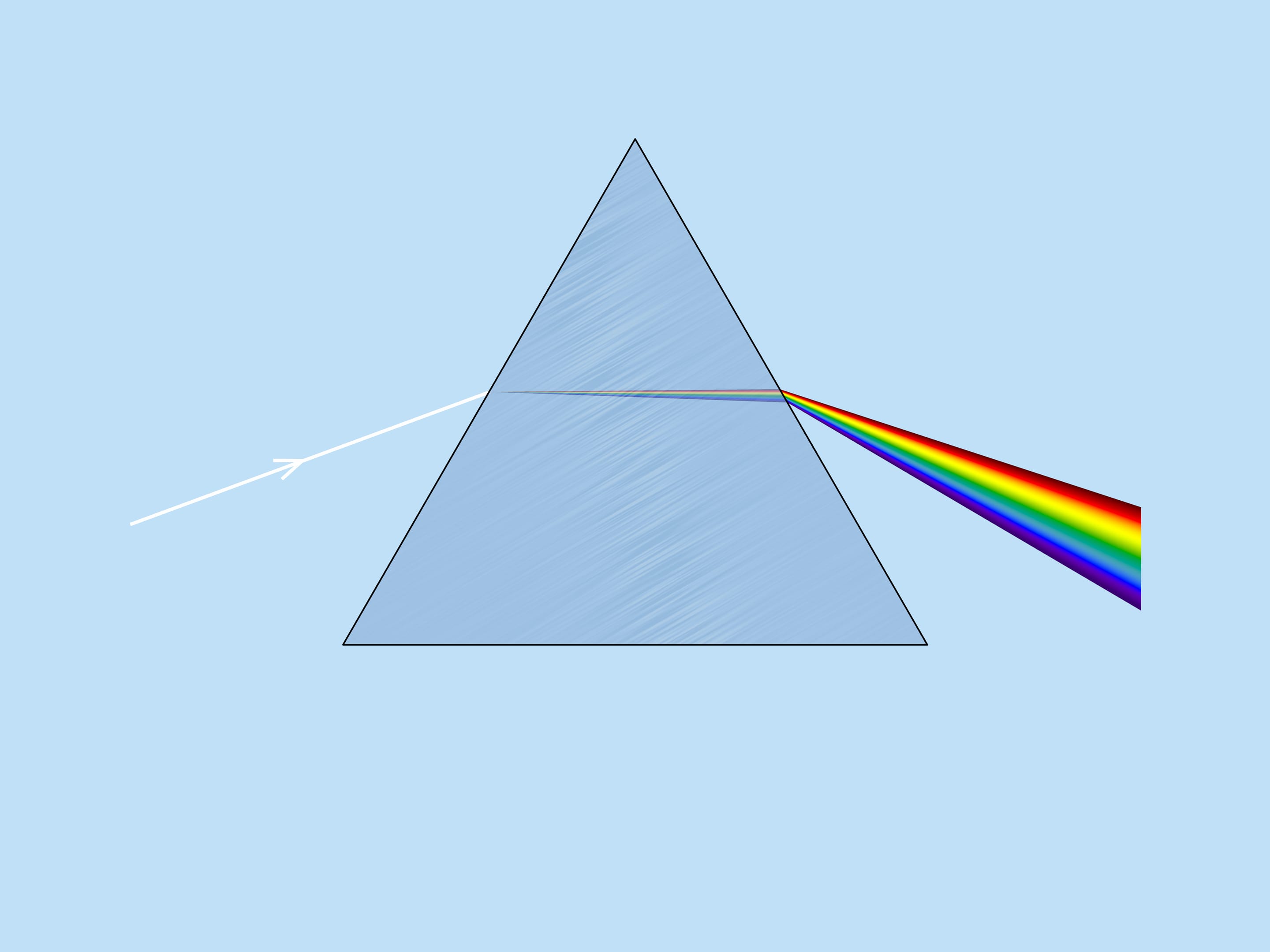
The great Isaac Newton, in his famous experiment with the glass prism, which is now essential to physics lessons, broke down the white sunlight into its color components and showed that the different colors correspond to different refractive indices. This effect is called light dispersion. And it is because of the dispersion the rainbow is multicolored.
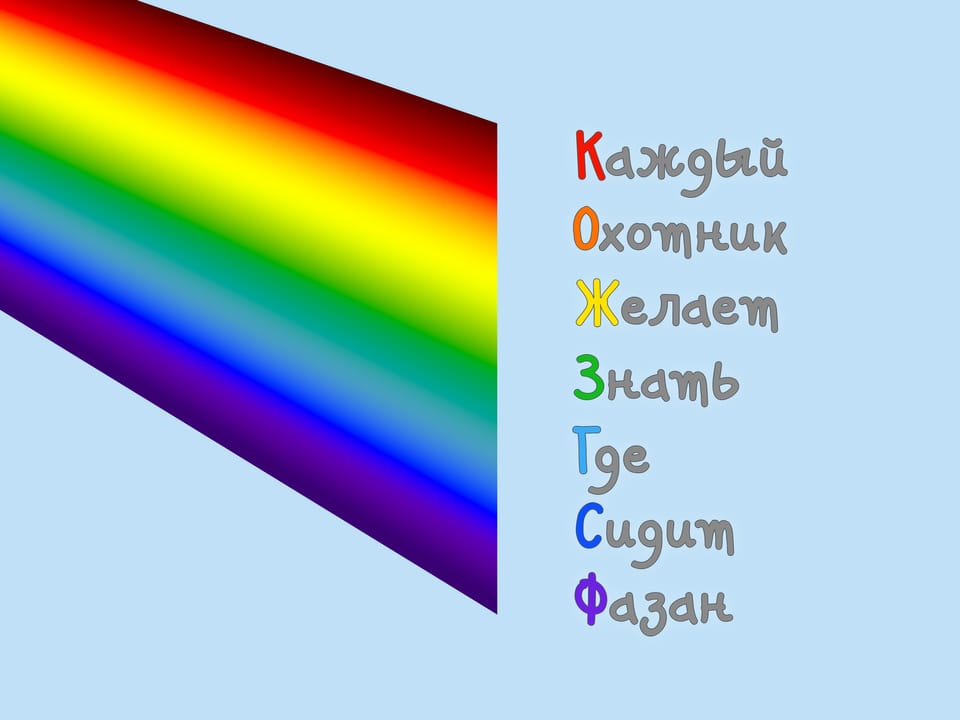
He distinguished seven components in the resulting spectrum: red, orange, yellow, green, blue, indigo, and violet. These colors are easy to remember with the well-known mnemonic rule, “Richard Of York Gave Battle In Vain (ROYGBIV)”. Interestingly, not all countries have seven colors of the rainbow. In Japan, for example, there are six.
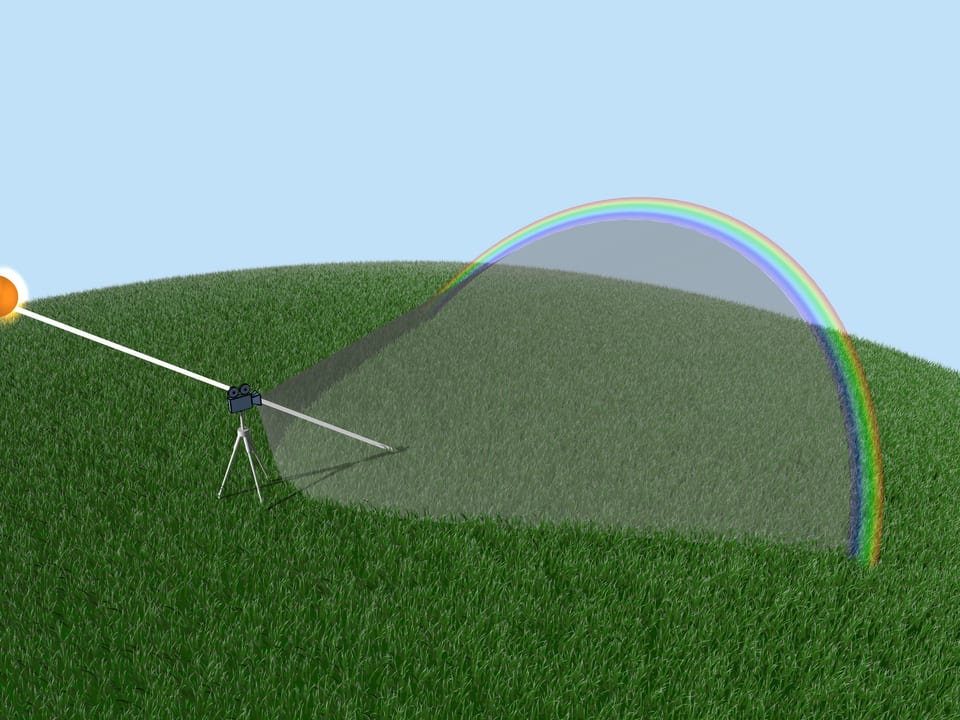
Rainbows are formed by raindrops in the air. To understand exactly how it happens, consider the path of the solar rays in a single droplet of water. Let’s assume that the droplet is shaped like a ball. (René Descartes conducted thousands of experiments with a glass spherical flask filled with water.) Because of symmetry, the path of a ray in a droplet depends only on its distance from the center of the drop. Consider the rays that lie in the plane “the Sun — observer’s eye — center of the drop”.
Since the Sun is located very far from the Earth, we can assume that its rays reach the Earth’s atmosphere parallel to each other, and the angle of their incidence depends only on the height of the Sun above the horizon.
The solar rays forming the rainbow enter the droplet from the air and then leave outside, experiencing a series of refractions and reflections. At the border of two media, in this case water and air, both refraction and reflection always occur. We will only consider such a path of the rays which is relevant to the rainbow formation.
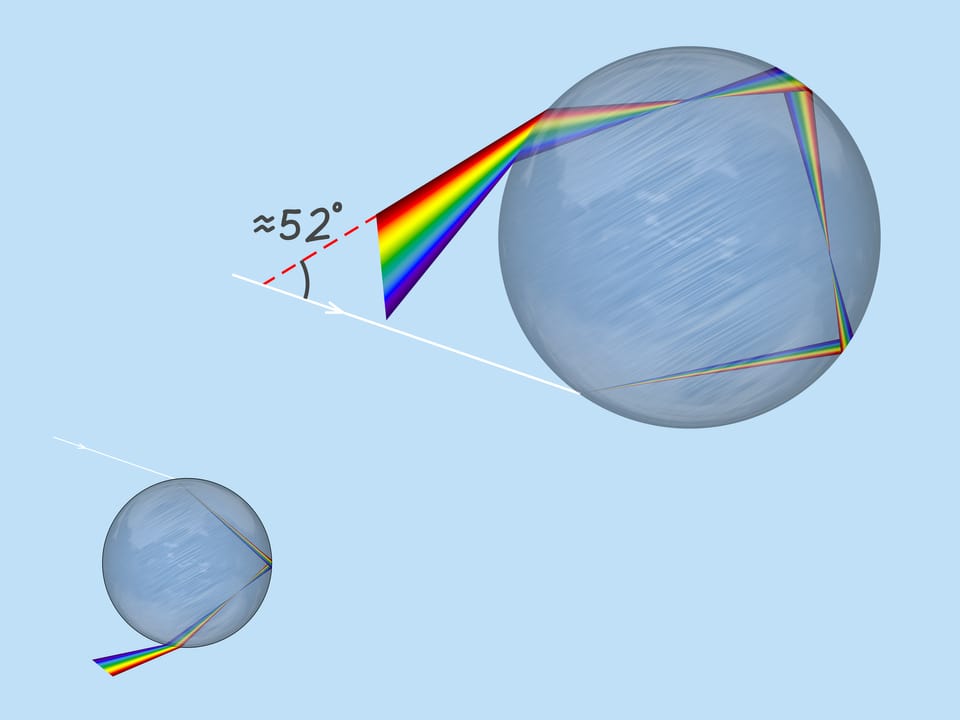
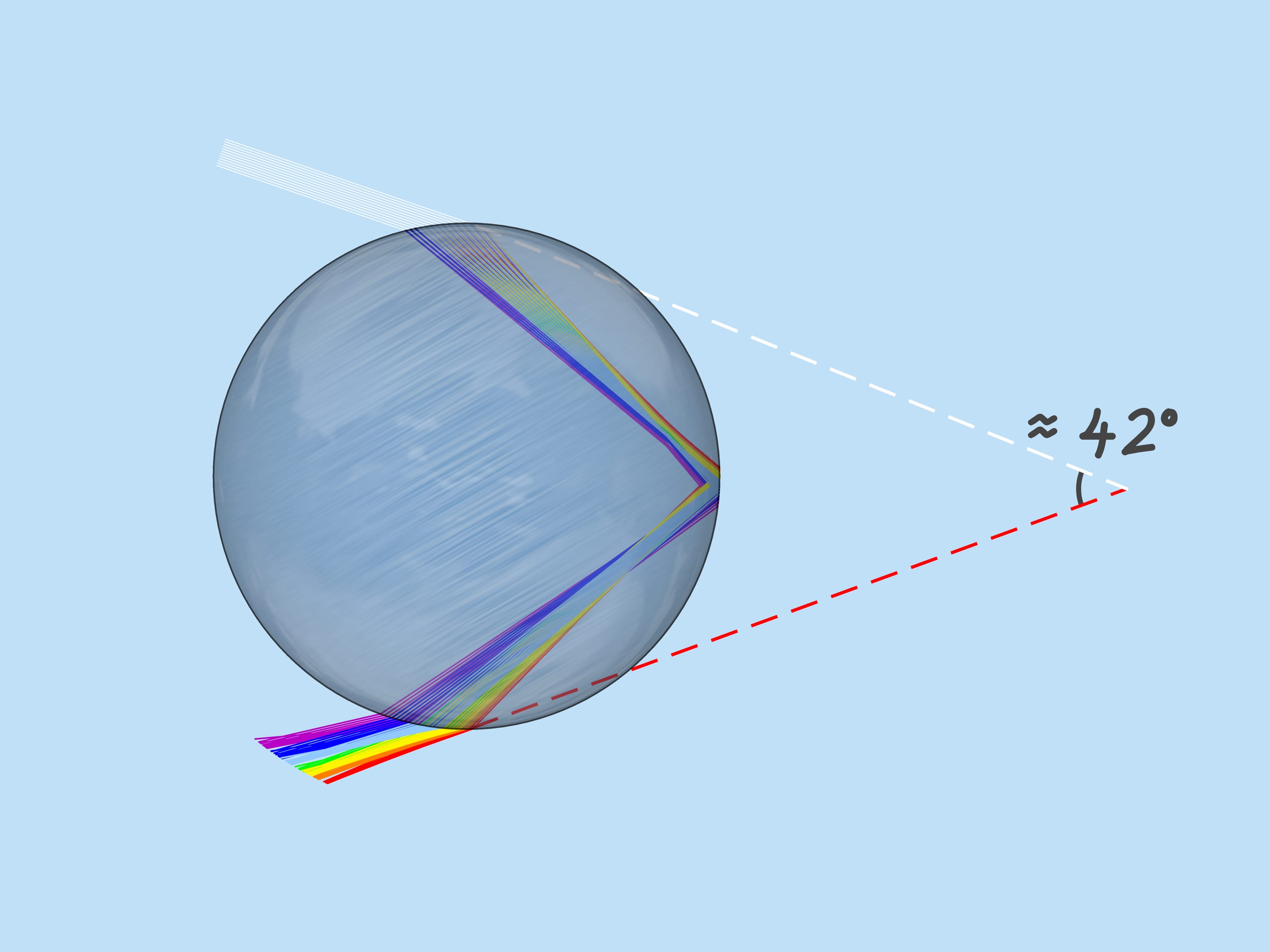
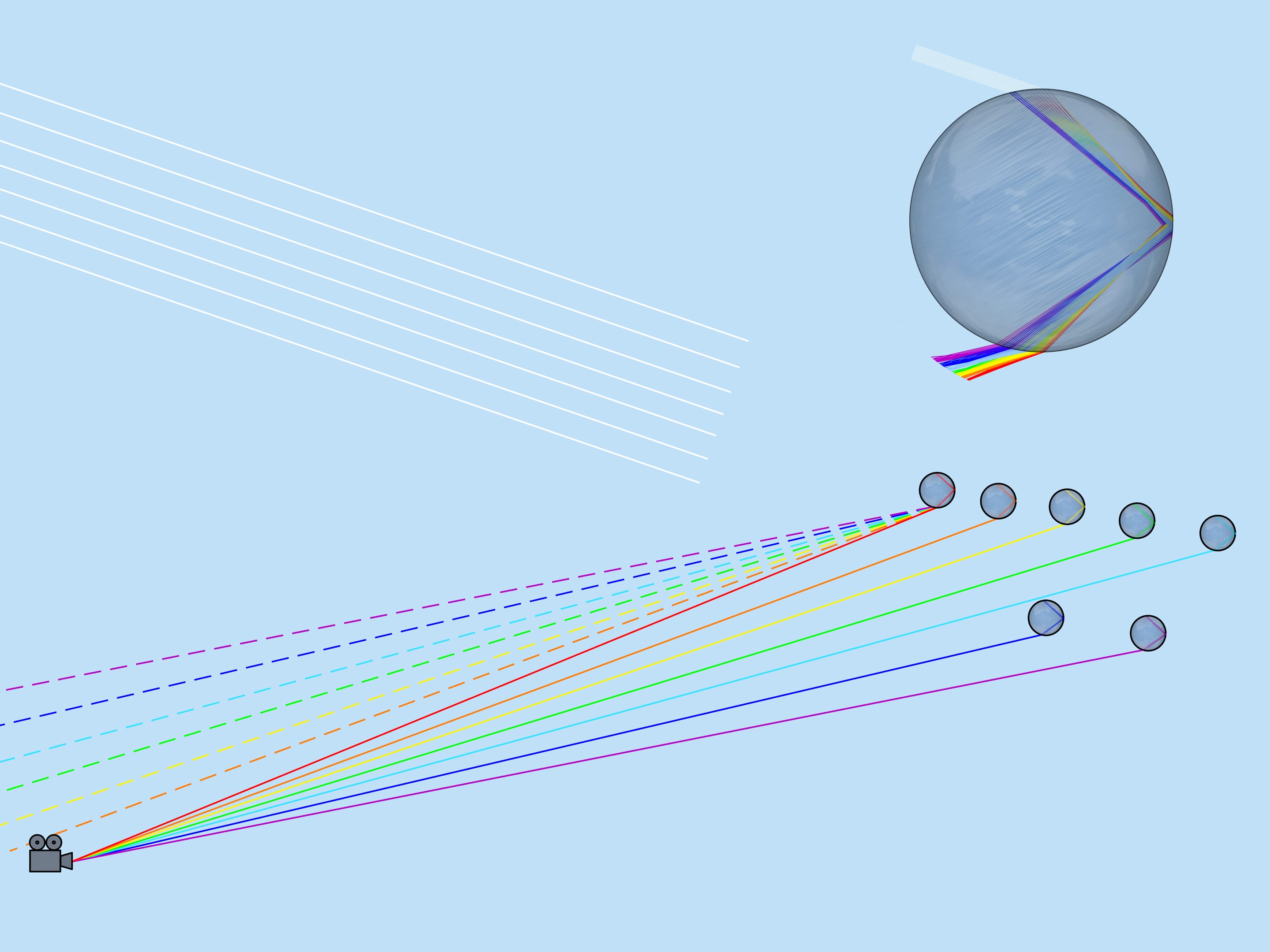
First, consider those rays that hit the upper half of the droplet. These rays are refracted on entering the droplet, then reflected from the back side of the droplet and, refracted again, go outside the droplet. As they refract, dispersion occurs and colors appear.
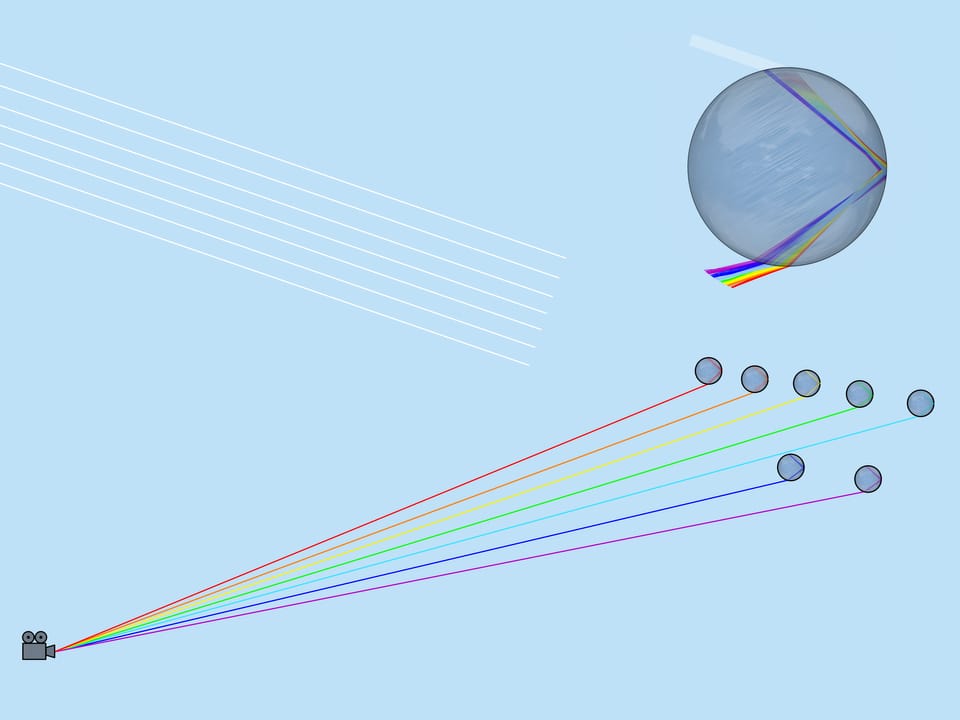
The rays fall uniformly on the surface of the droplet facing the Sun. On leaving the droplet, the rays are distributed nonuniformly. Let’s see which rays form a rainbow.
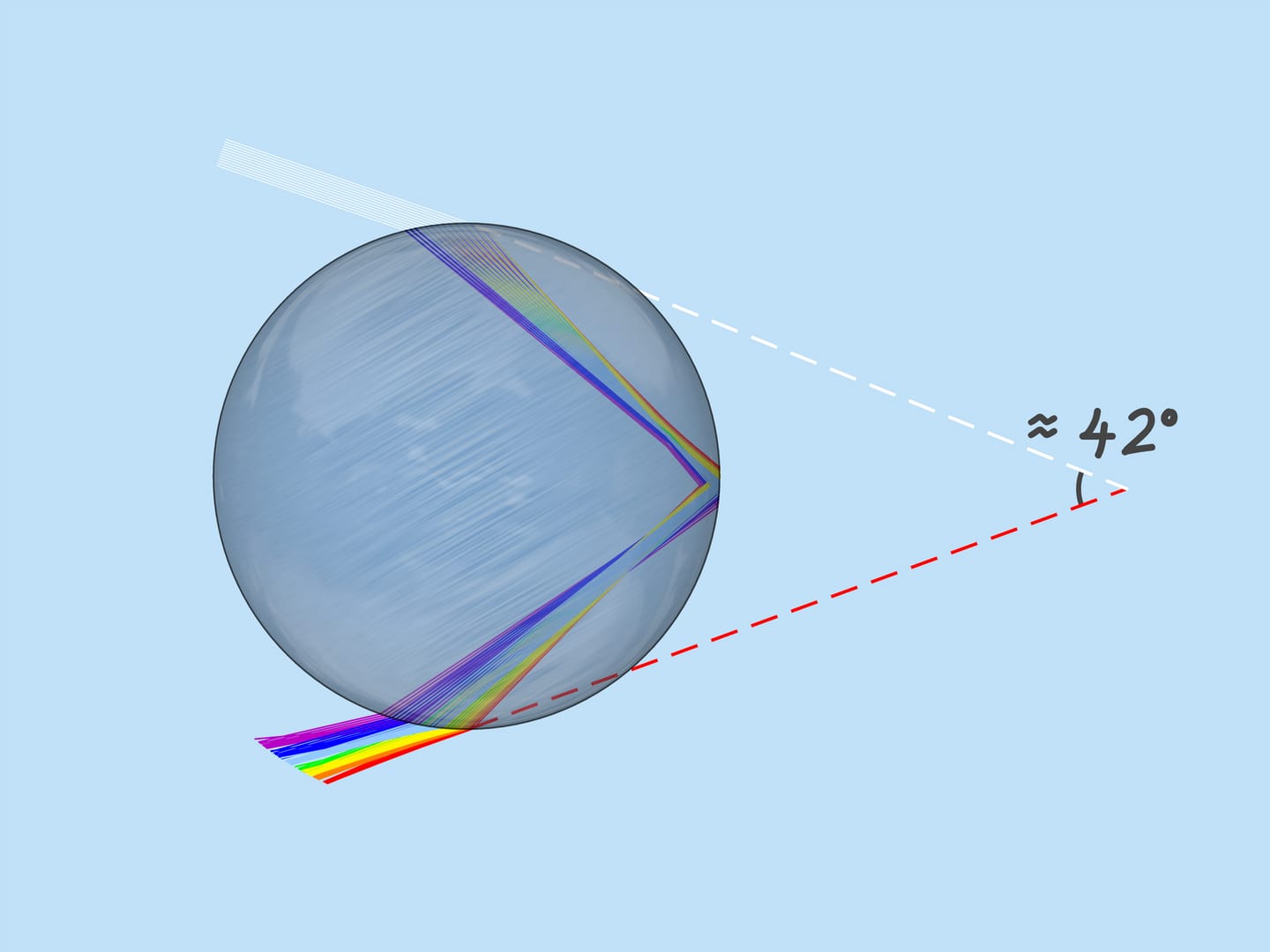
The ray that hits the droplet exactly in the center is not refracted (because the angle of incidence is $0^{\circ}$). Reflecting off the back side of the droplet, it will leave toward the incident ray. Rays that hit the droplet close to its center are not refracted much (because their angle of incidence is close to $0^{\circ}$). After reflection, these rays emerge almost towards the incident rays, deflected from the return in the opposite direction by a small angle. As the incoming rays move away from the center of the droplet, this angle increases, but at some point a maximum is reached: the rays distant from the center by about $0{,}86$ of the droplet radius are deflected the most. Further away from the center of the droplet, as far as those rays just touching the droplet, the angle decreases.
For the red rays, the refractive index in the film was taken to be $\textit{1,33}$, which conforms to reality. For all other colors, the refractive indices have been slightly increased relative to the real ones for clarity.
Near the maximum (or, as mathematicians say, extreme) value, the deflection angle changes slowly, so there is an “accumulation” of outgoing rays. These rays are what are perceived as rainbows.
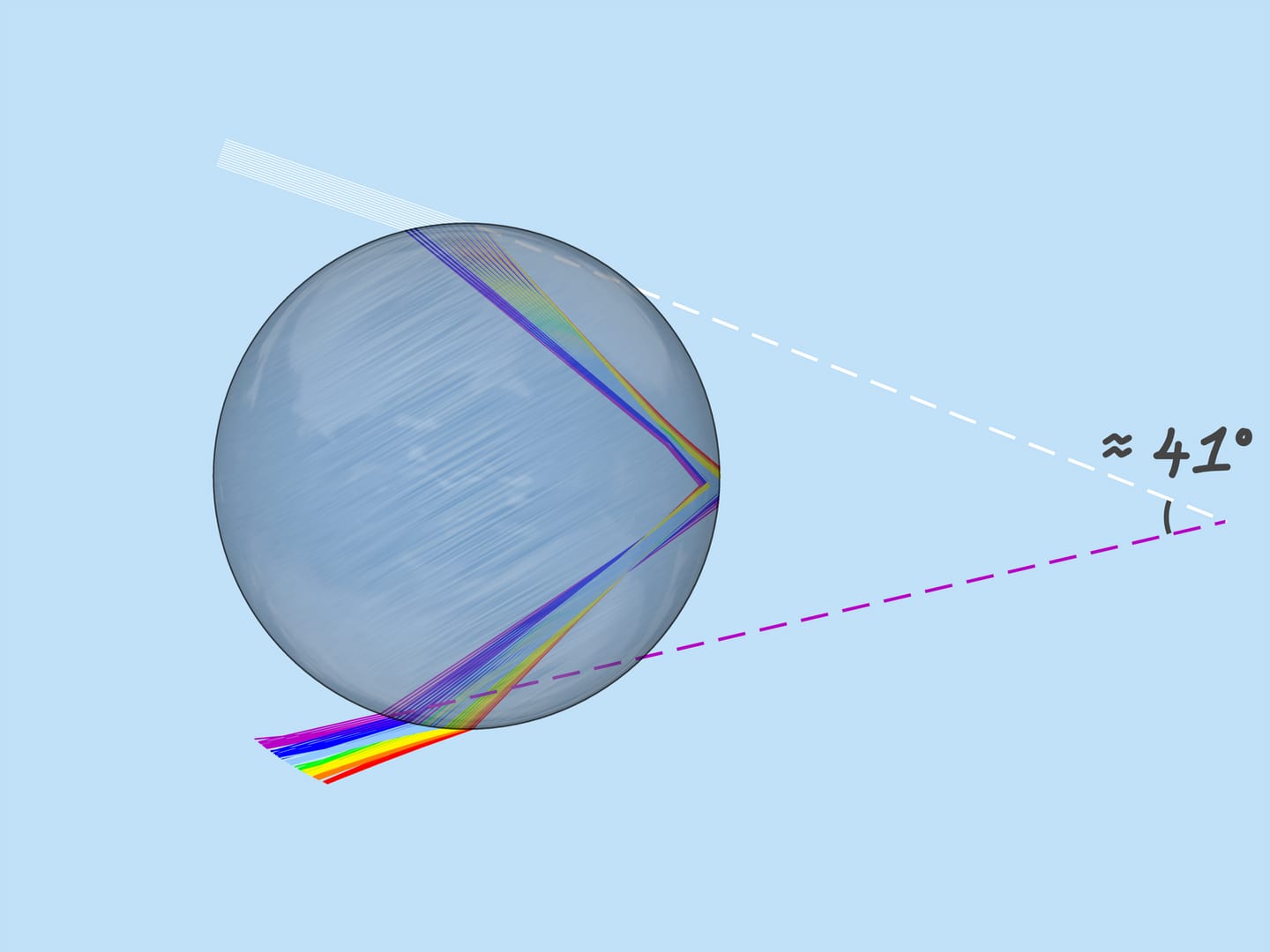
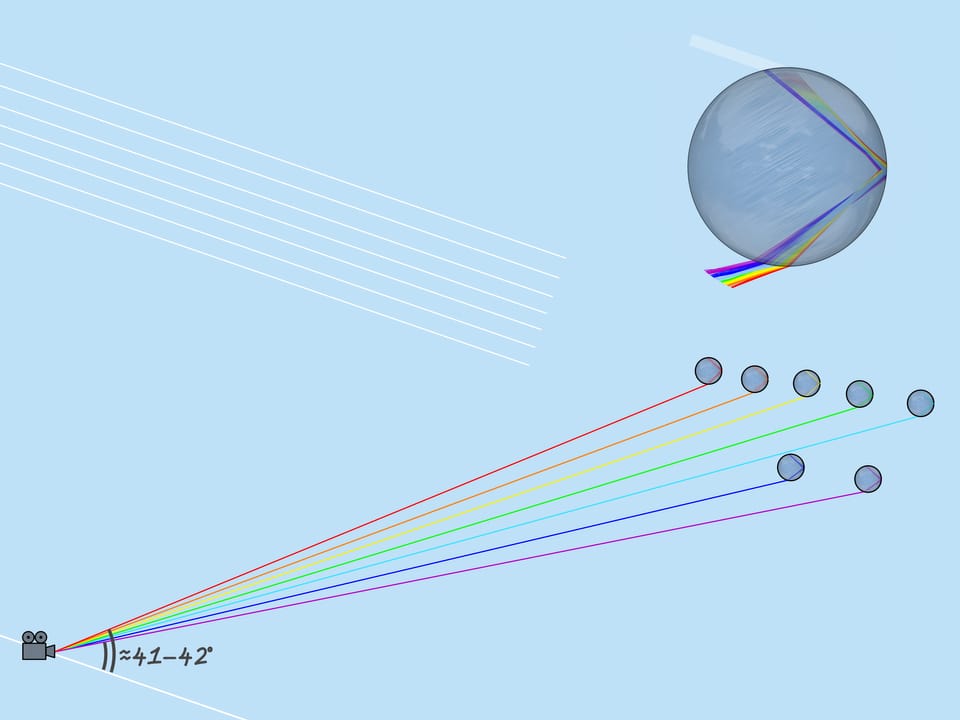
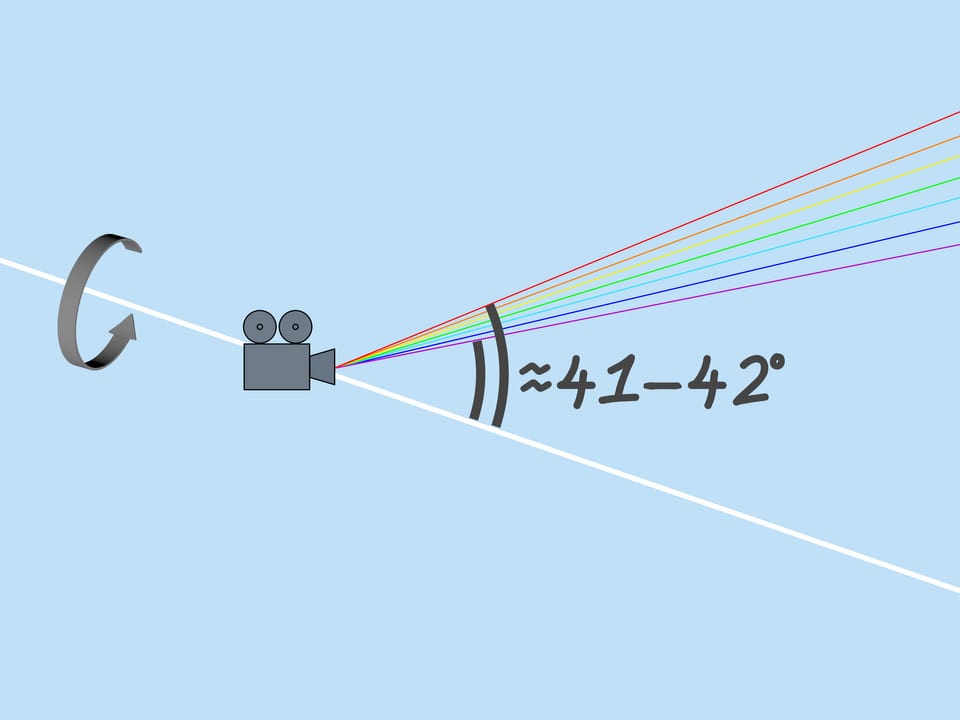
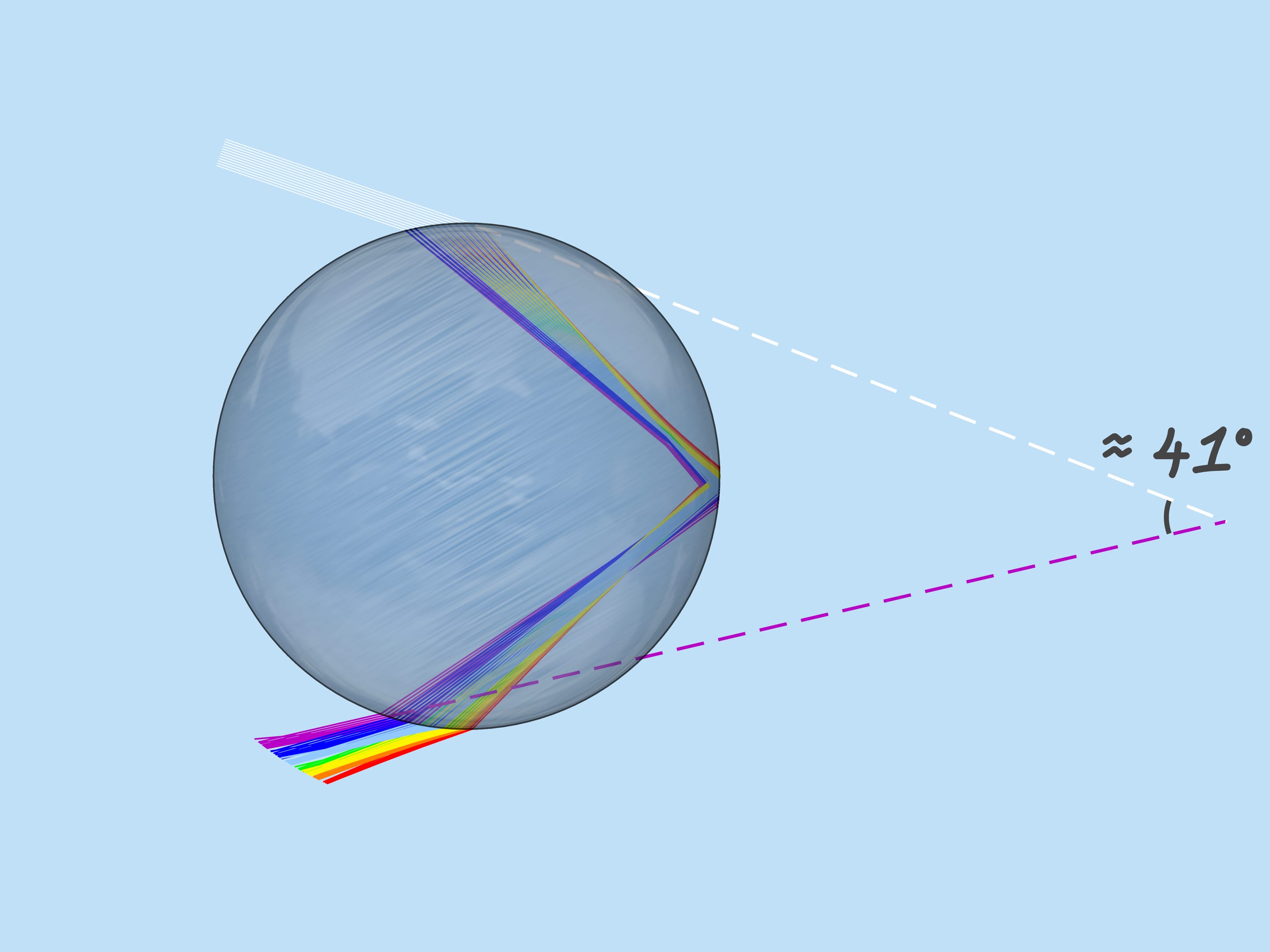
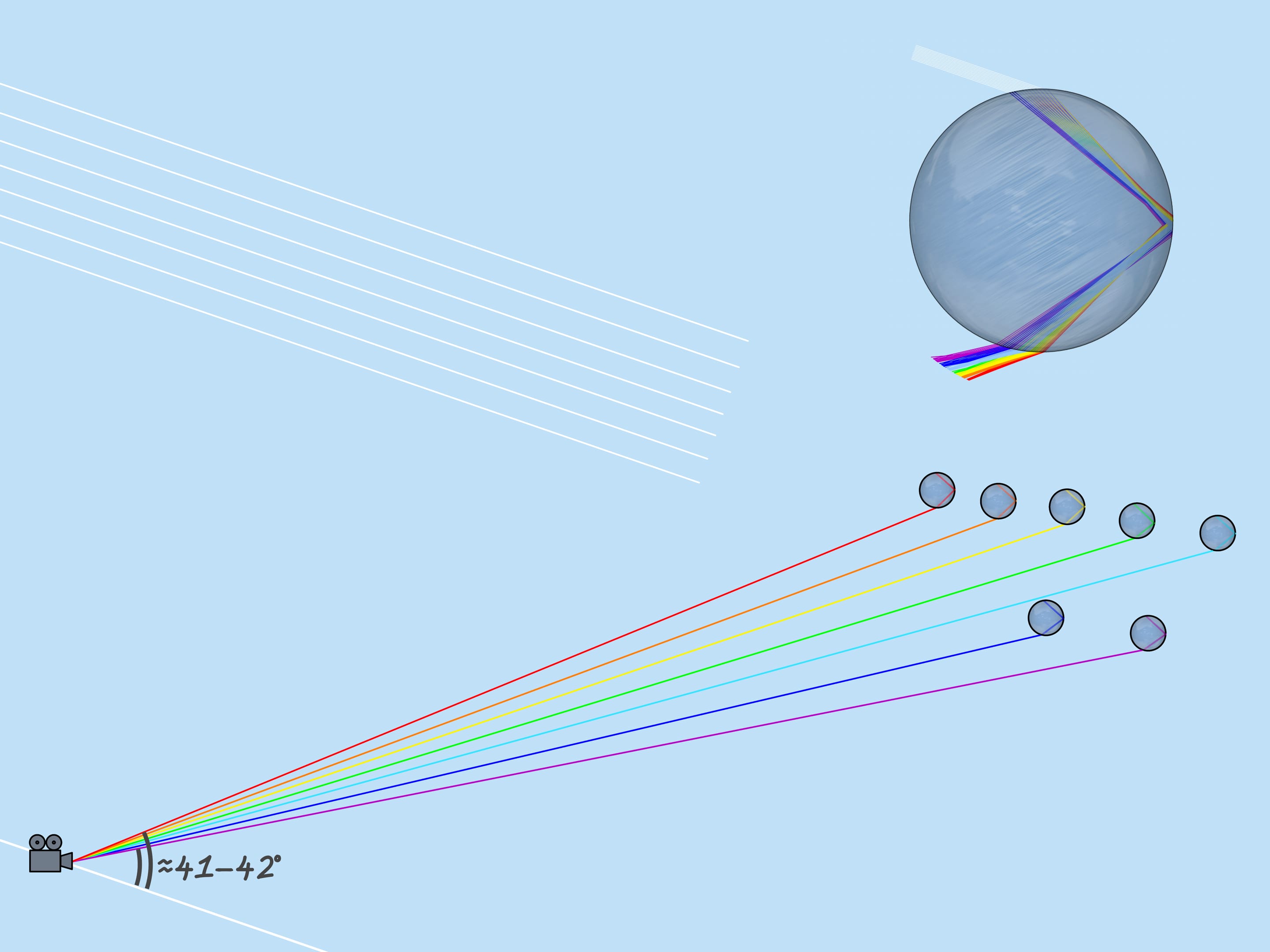
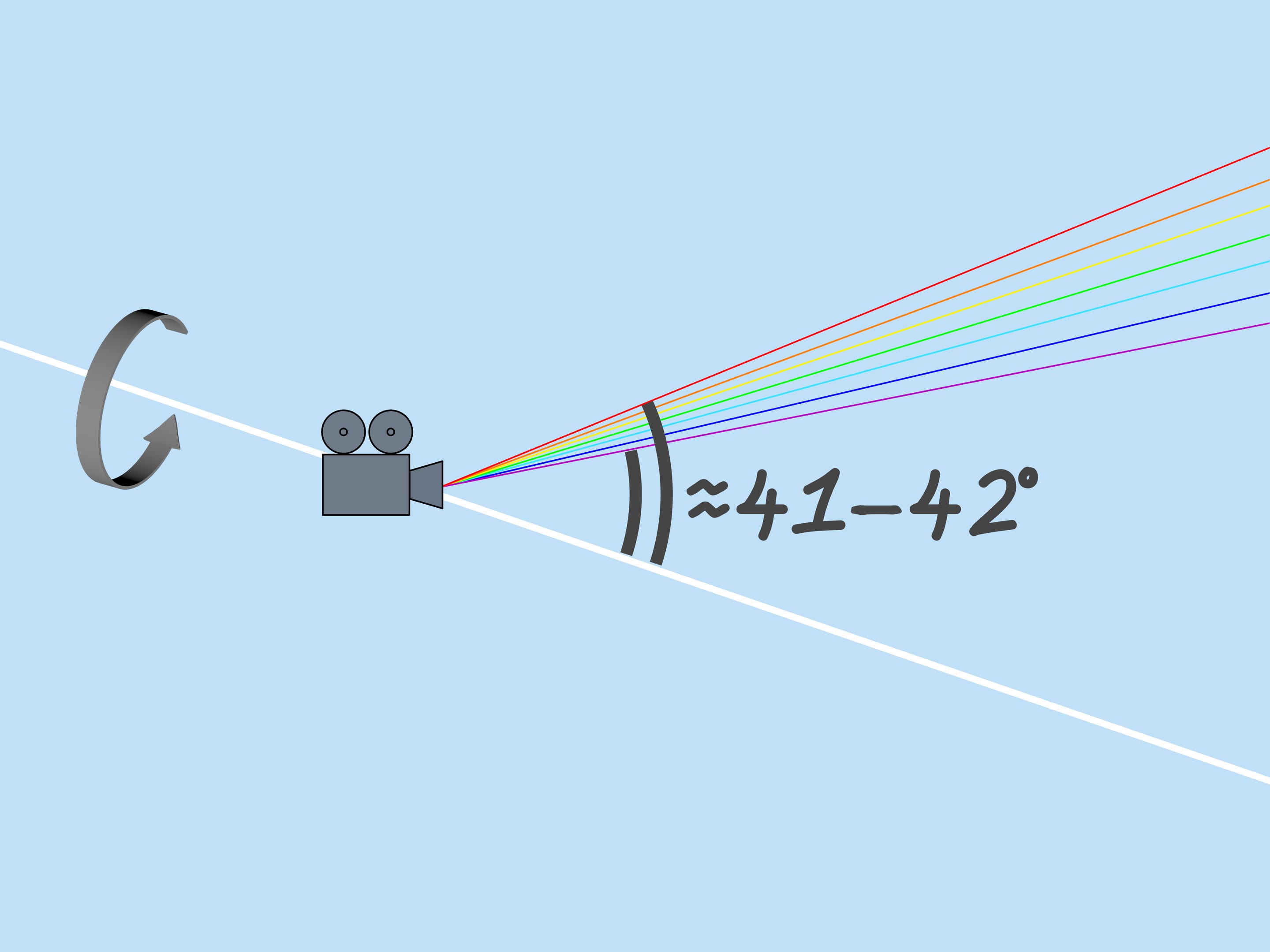
As mentioned above, the refractive index for the rays of different colors is different, so the maximum deflection angle is also different. For red, it is about $42^{\circ}$. And for violet, it’s $41^{\circ}$. The rays of the other colors lie between $41^{\circ}$ and $42^{\circ}$.
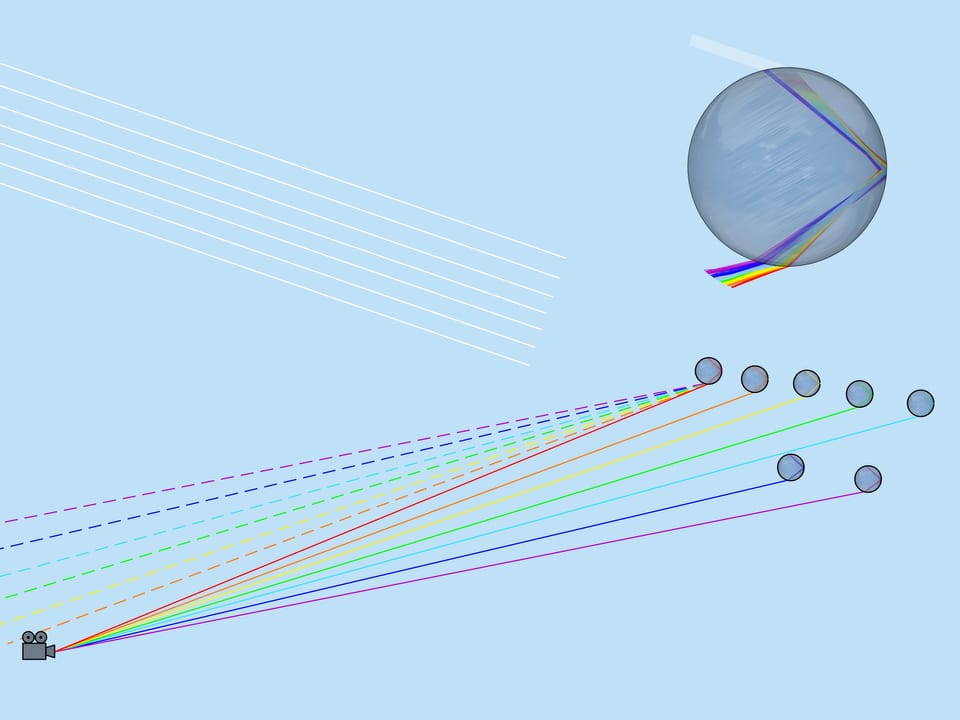
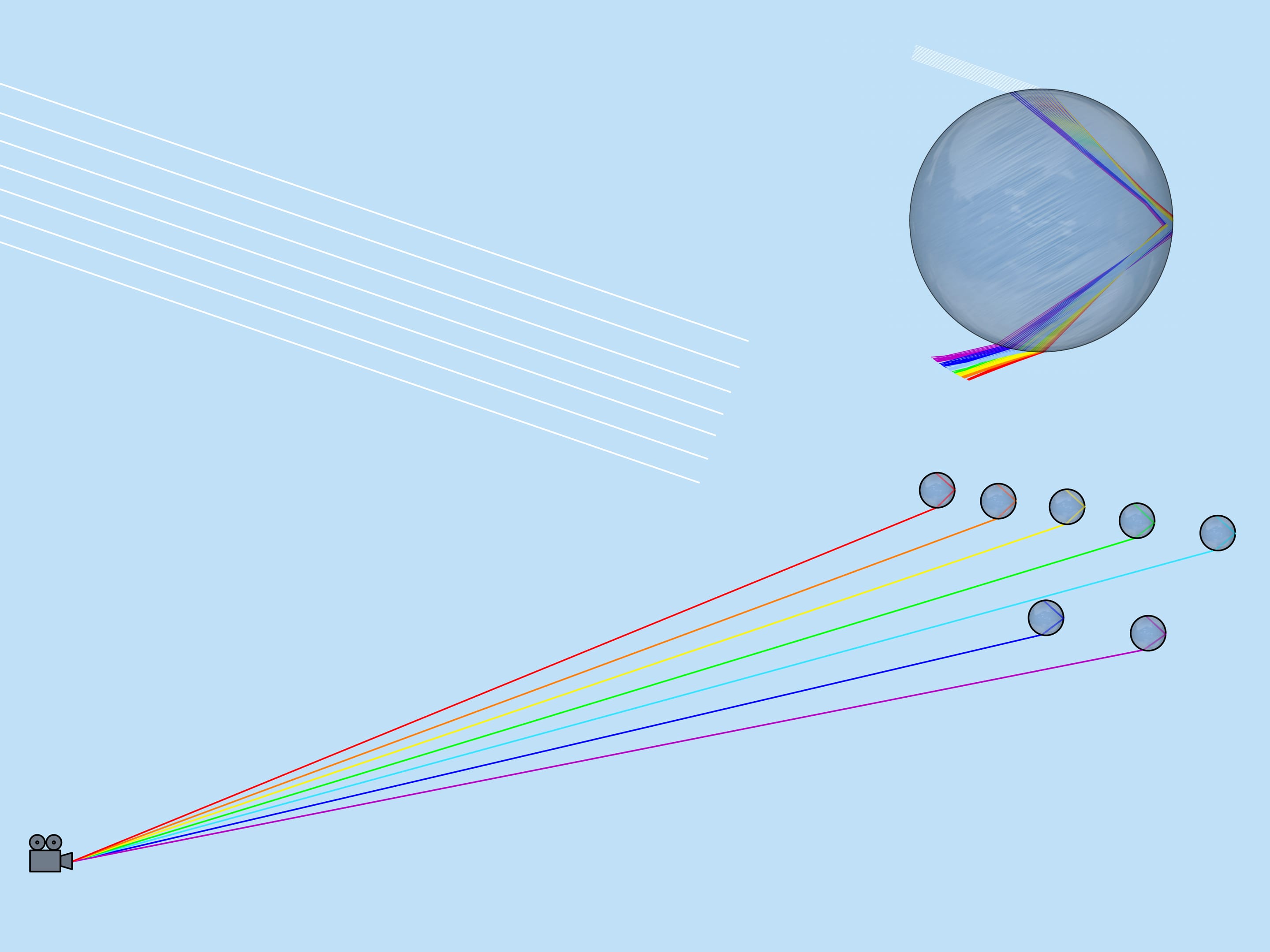
Looking at the picture of light rays passing through a droplet, we will notice that if for example yellow color came to the observer from the given droplet, no other color can come from this droplet (red will go lower, and blue will go higher than the observer). Thus only one color is visible from each droplet.
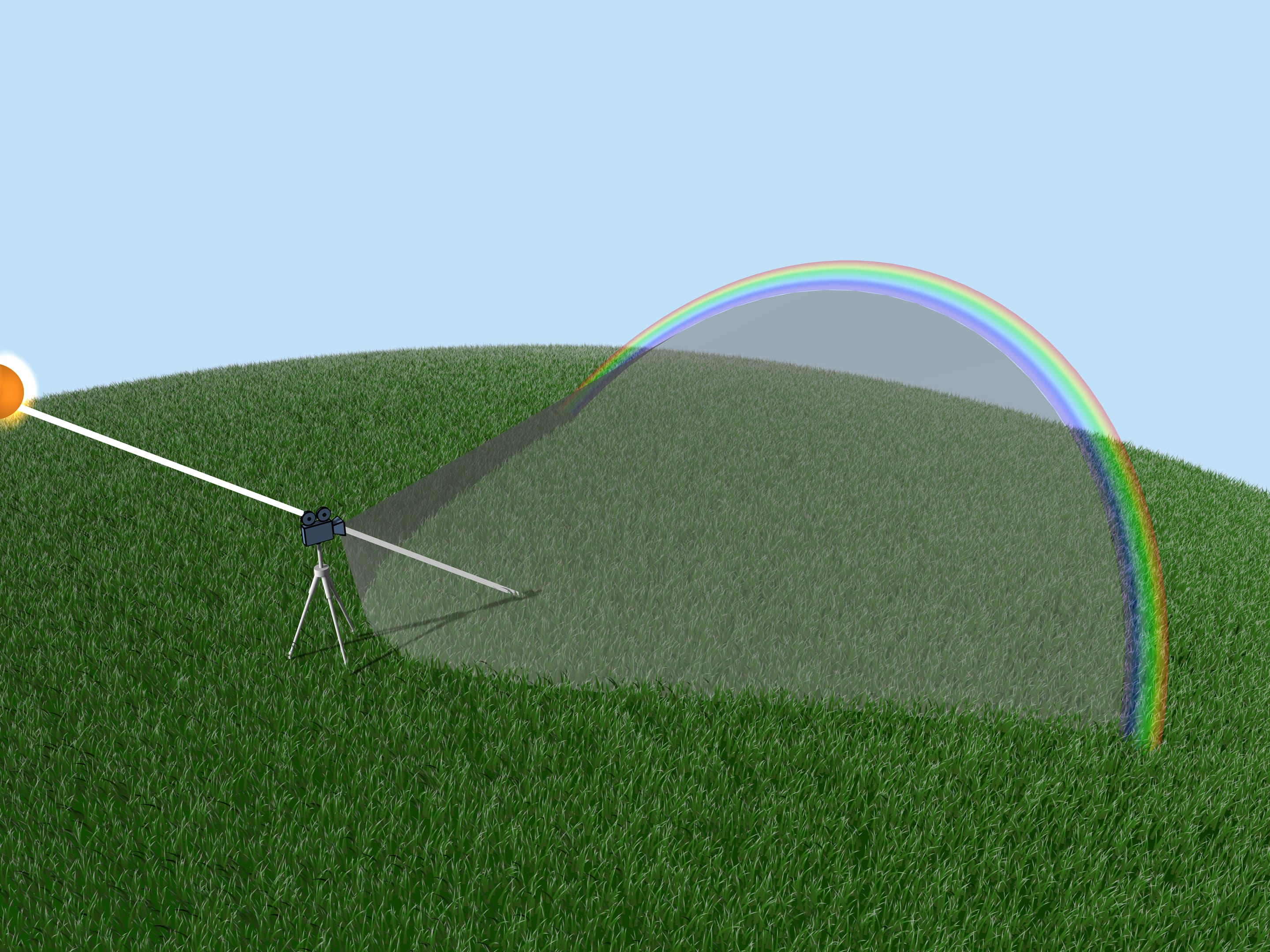
Now consider the whole multitude of raindrops. Which raindrops are responsible for the formation of the rainbow color? From the above it is clear that, for example, the violet color is formed by those and only those droplets that lie on the straight line forming an angle $42^{\circ}$ with the coming to the Earth solar rays. So, the violet color of the rainbow lies on the surface of the cone with the vertex in the observer, the axis being a continuation of the segment “the Sun — observer’s eye”, and the aperture $42^{\circ}$. Other colors also lay on surfaces of cones with the same axis and corresponding to these colors aperture.
If an observer looks at the rainbow, then the Sun is behind him. The rainbow is said to be at the “anti-solar point.” The height of the rainbow depends on the position of the Sun. The largest rainbow is seen when the Sun is close to the horizon.
Now consider the solar rays hitting the lower part of the droplet. Due to symmetry, the above reasoning can be almost completely replicated. But then the solar rays go upwards on leaving the droplet, and the observer on the Earth cannot see them. However, another path of a solar rays in the droplet is also possible! The rays may reflect twice from the back side of the droplet and then leave it.
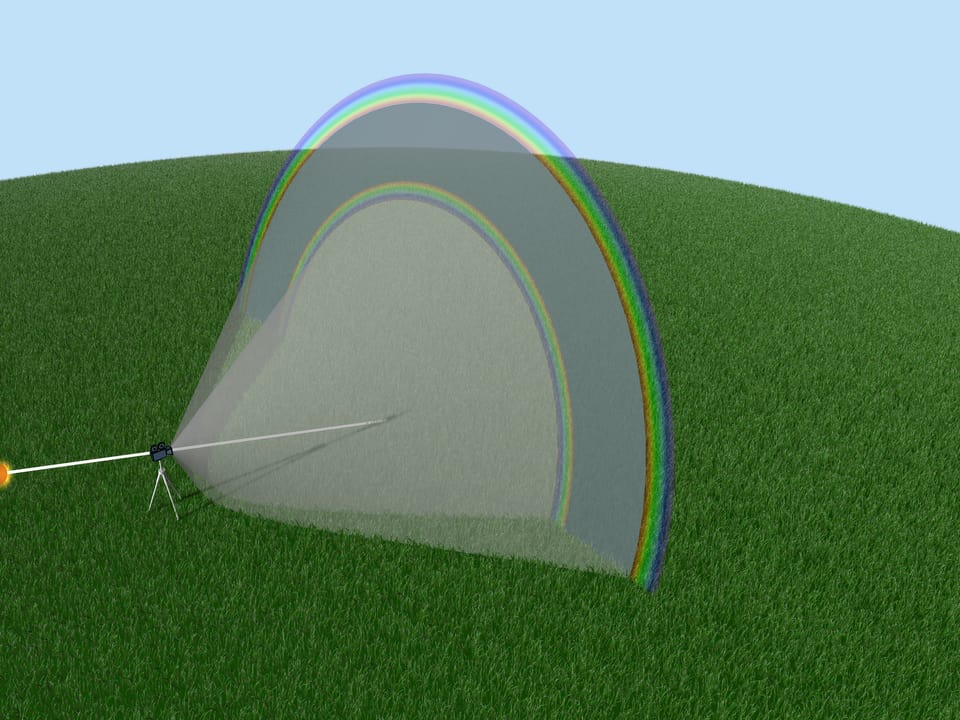
This path of the solar rays produces a second rainbow. The second rainbow can be seen at an angle of about $52^{\circ}$ to the “the Sun — observer’s eye” direction. Thus, it is higher than the first rainbow. Since the rays were reflected from the sides of the droplet twice, the order of colors is reversed: red at the bottom and violet at the top.
With each reflection, the intensity of light decreases, so the second rainbow is less vivid than the first. Theoretically, the third rainbow and higher order rainbows also exist, but they are not visible under normal conditions because they are produced by many reflections in the droplet.
An attentive person will notice the dark area of the sky located between the first and second rainbows. The fact is that after interacting with the droplets, only small numbers of rays come to the observer at angles from $41^{\circ}$ to $52^{\circ}$. Another sign of the rainbow that is not always noticed is the light and dark stripes just below the violet arc of the first rainbow. However, their explanation goes beyond geometric optics.
It is impossible for an observer standing on the Earth to see a full circle of the rainbow in the sky. The full rainbow, the whole circle, can be seen in a fountain splashes not too high above the ground. In the sky, a full rainbow can be seen from an airplane.