Train wheels ⁠

Many boys wanted to go into the train driver cab. In fact, going in a straight tunnel, which is simply a cylinder, it is not so exciting. But some­thing different are the bends.

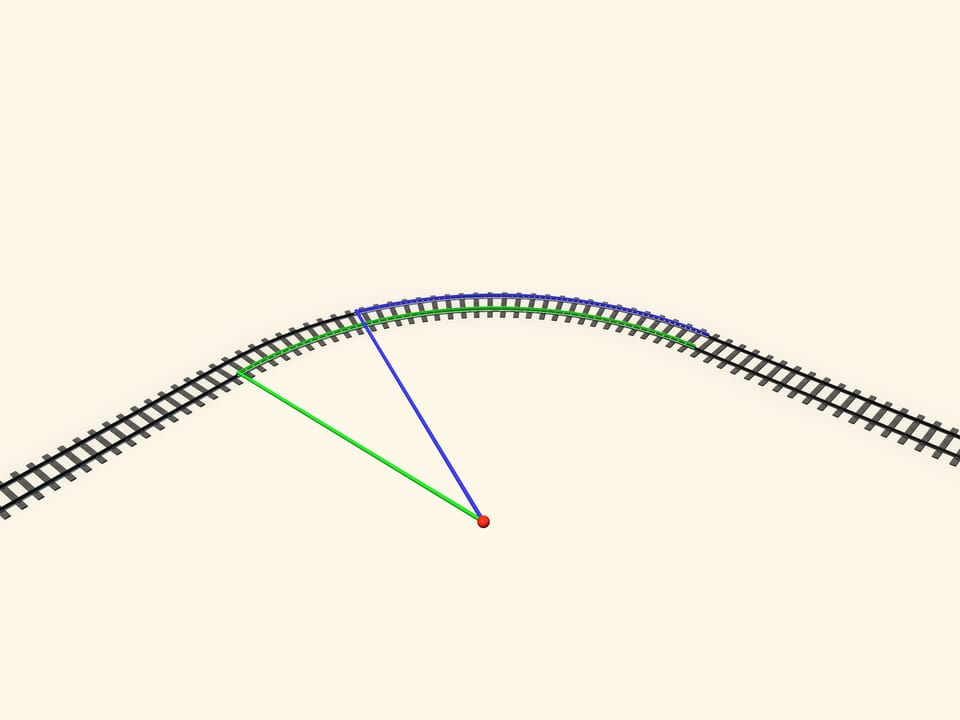
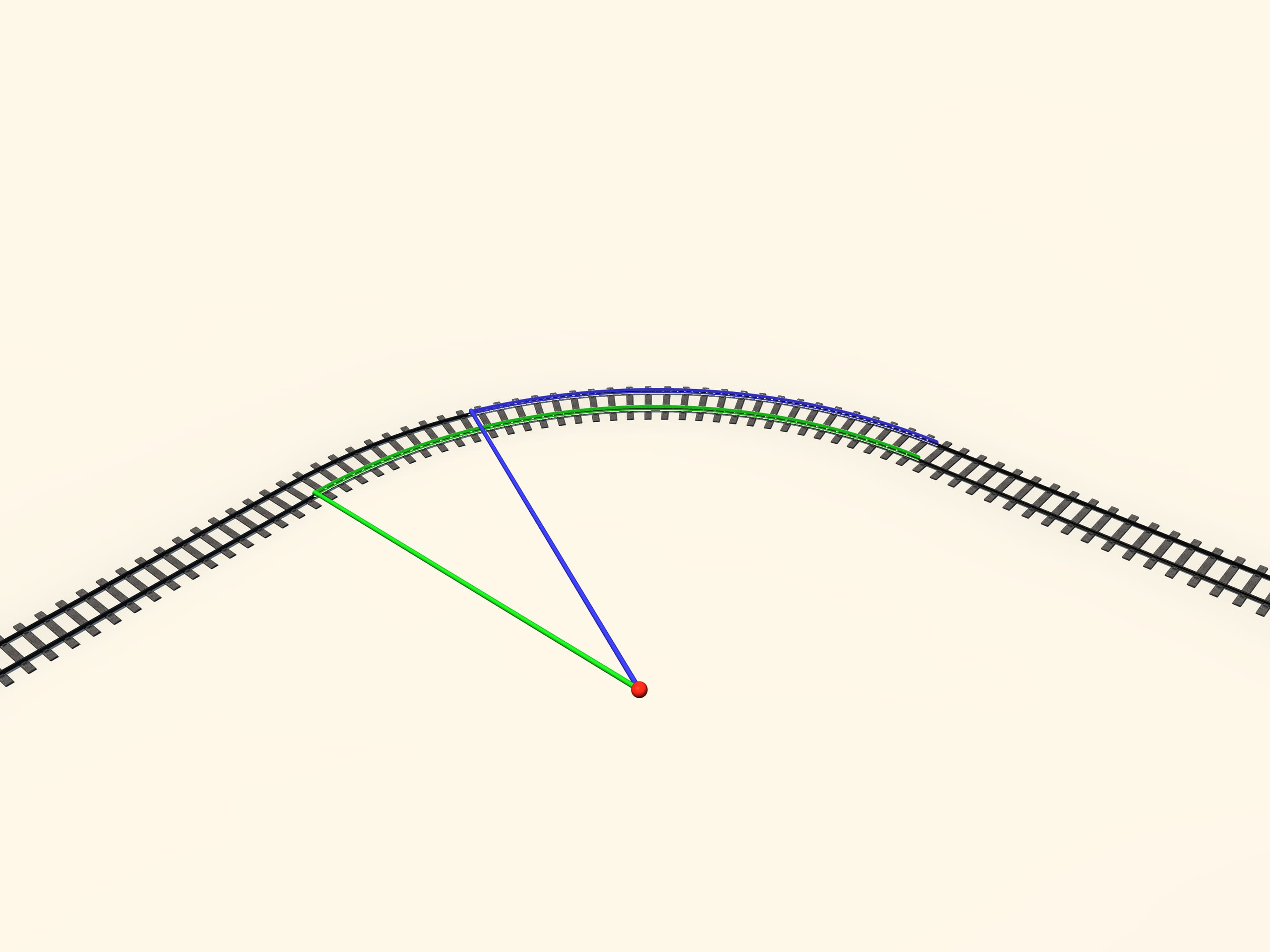
But in which manner the train wagons corner on the rails? In fact, the right and left wheels are rigidly attached together. More­over, in a curve the radius of curva­ture of the outer rail is greater than the radius of the inner one, so the length of the arc of a circle which is covered by the outside wheel is greater than the length of the arc covered by the wheel inside. And it is neces­sary that none of the two wheels skid on the rail.

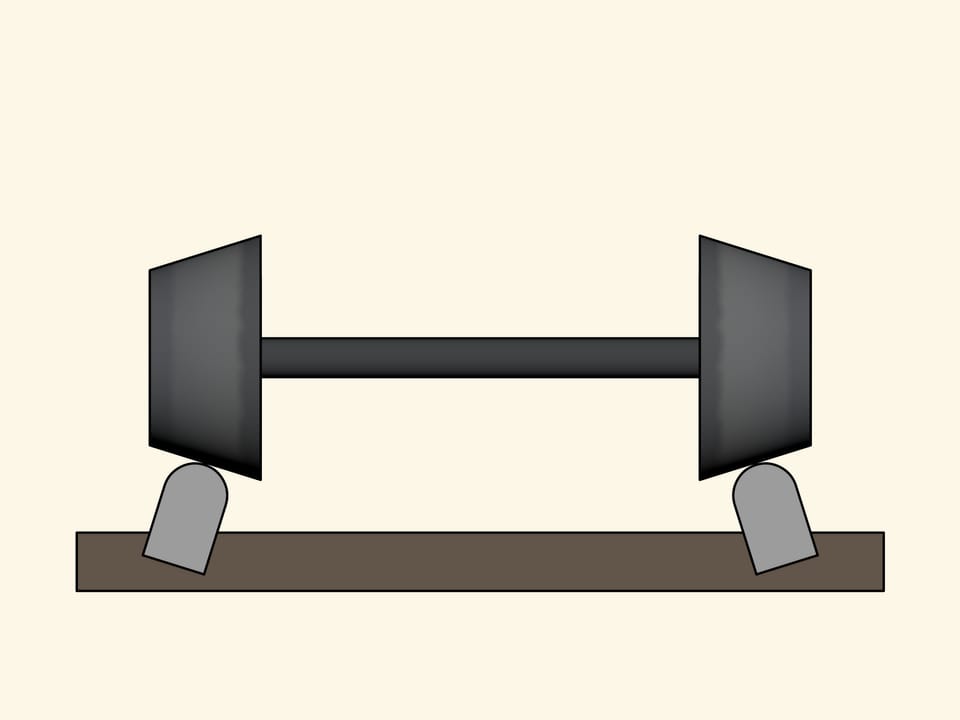
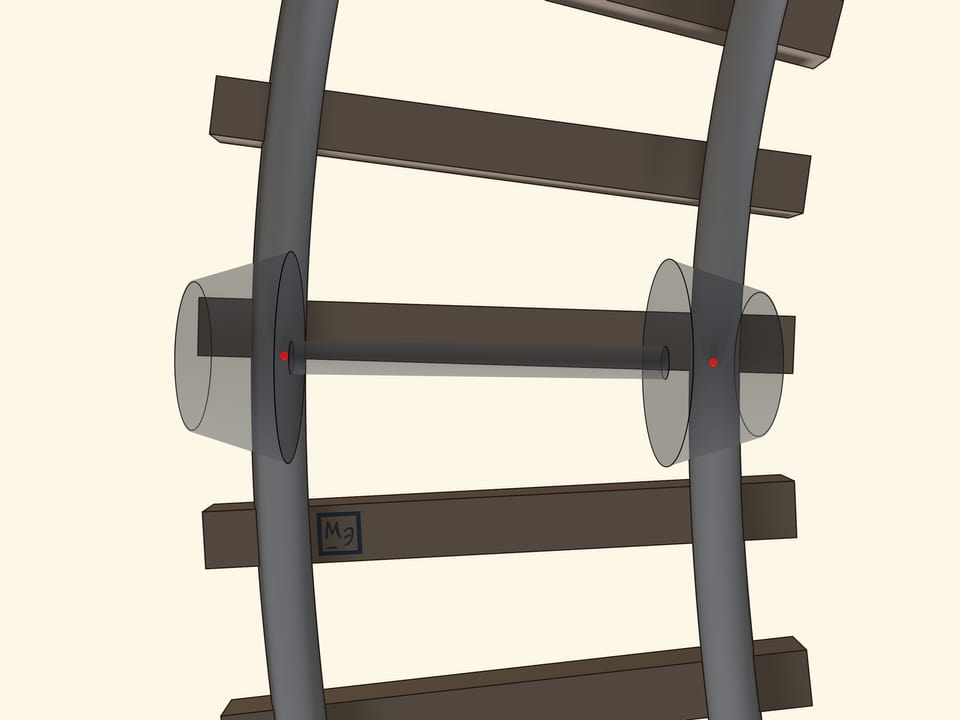
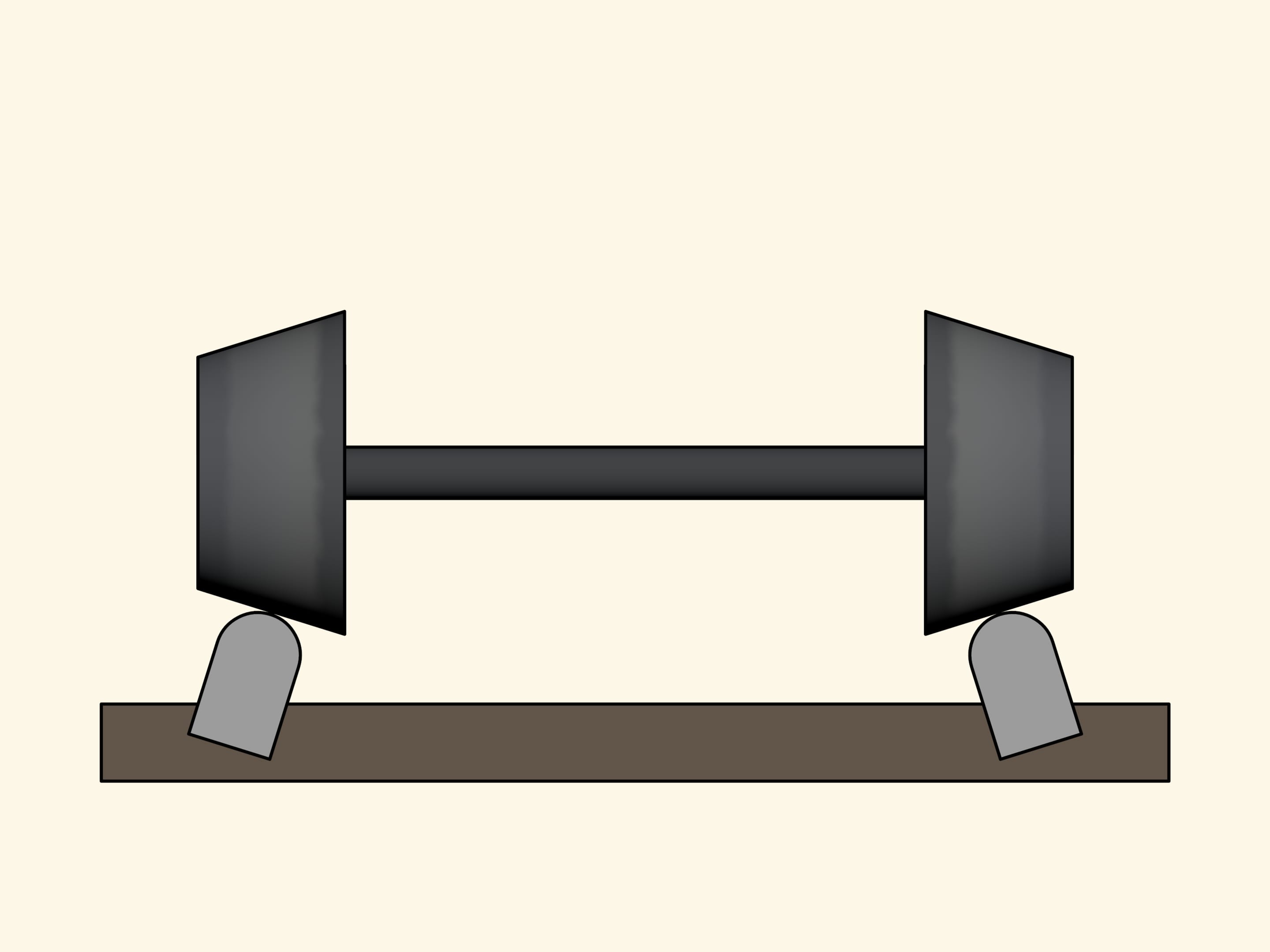
Consider a simpli­fied model which never­the­less explains well what essen­tially happens. The wheels in this model are two iden­tical trun­cated cones and are rigidly fixed to the axis. The profile of the rail surface is an arc of a circle. If the rails were embedded verti­cally, they would suffer an extra boost, since the load of the wheel affects on the rail perpen­dic­u­larly to its surface. There­fore, the rails are embedded a little inclined inwards, so that the axis of their profile is perpen­dic­ular to the surface of the conical wheels.

Let us follow a pair of wheels while passing on a bend. It happens that they shift with respect to the track!

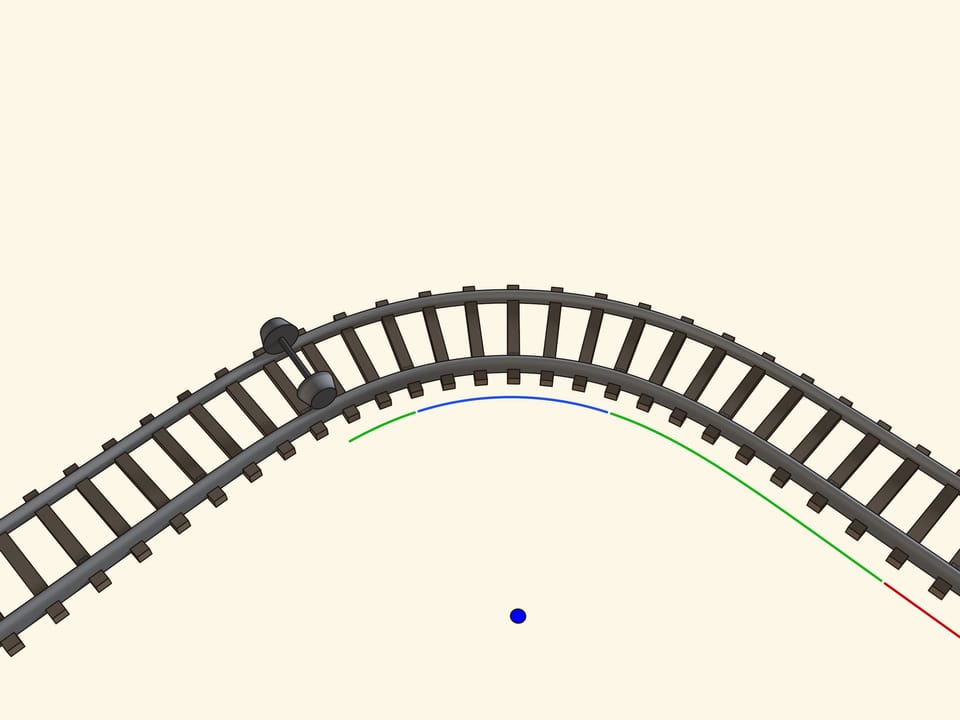
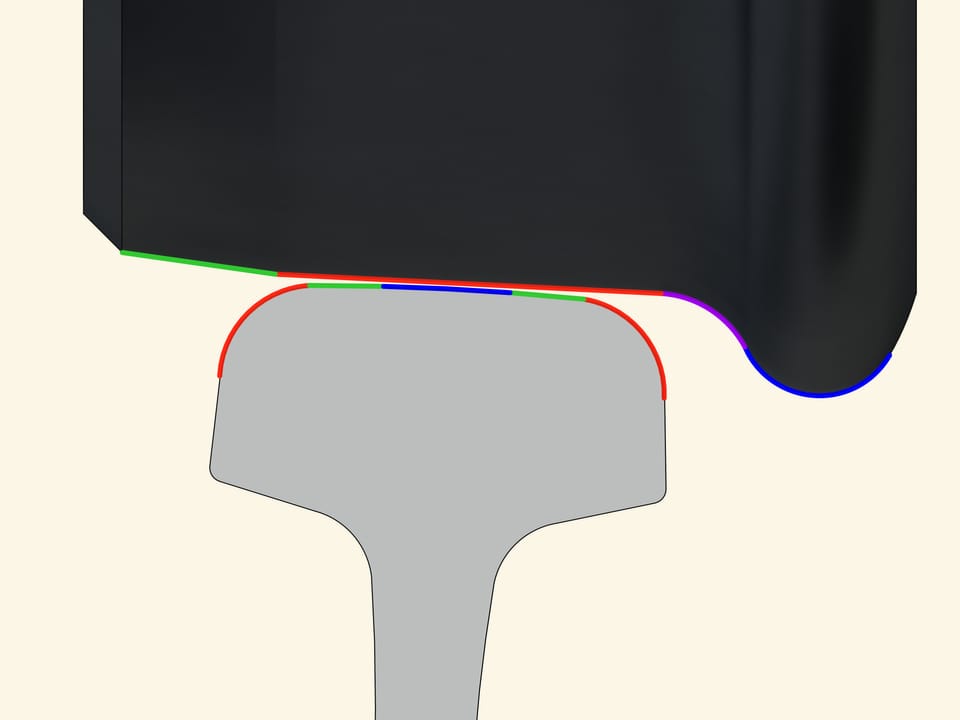
Observe how a curve is made. After a straight stretch begins a curved one with a vari­able radius of curva­ture, then there is a piece with constant radius, i.e., an arc of a circle. To ensure that passen­gers do not suffer jolts from the sides of the wagon while passing between two different stretches, a strong condi­tion must be satis­fied: the second deriv­a­tive of the trajec­tory must be contin­uous at the points of tran­si­tion between two consec­u­tive stretches.

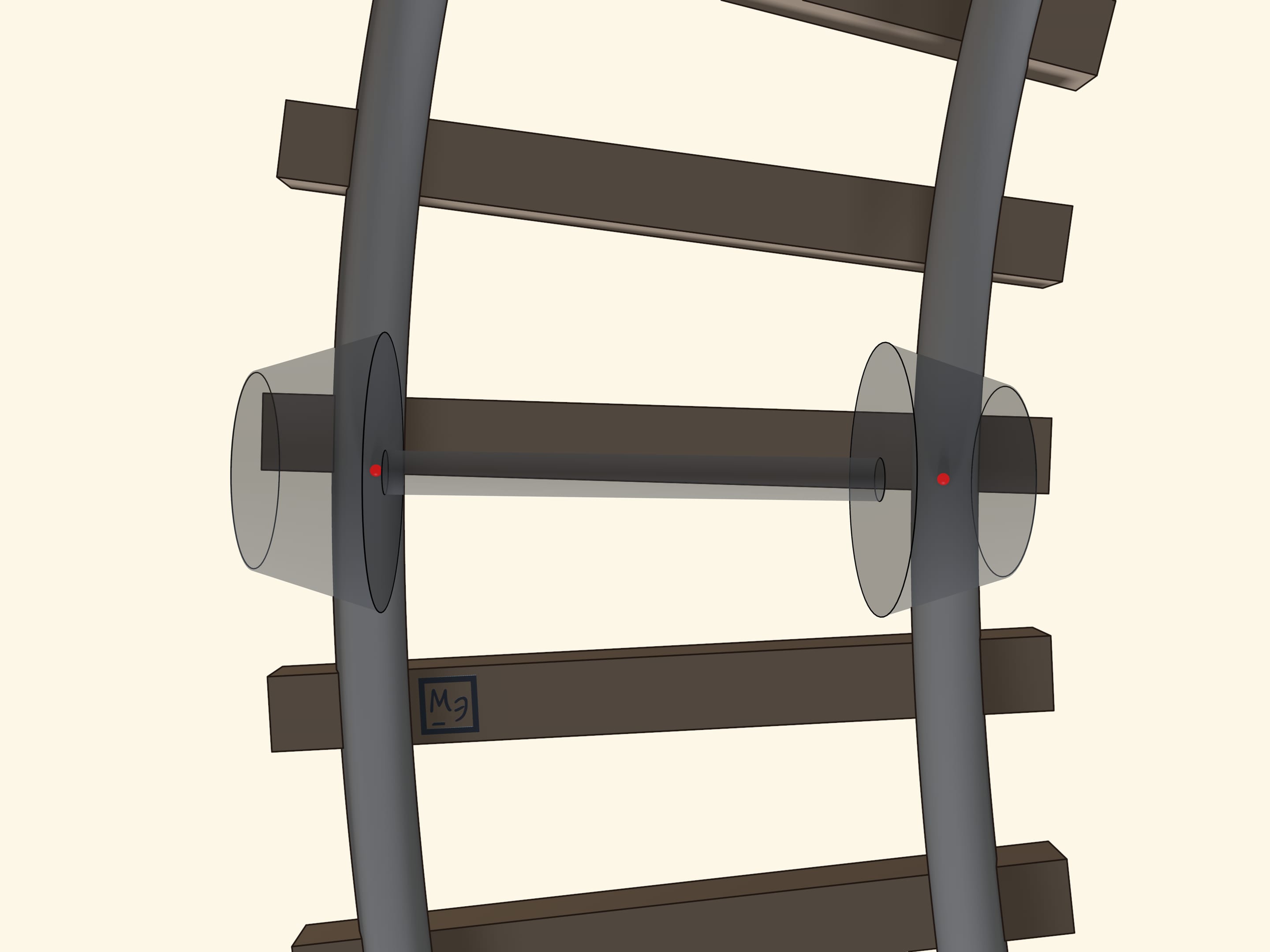
The tangency between the conic wheels and the rail surface is made by points. Moving on a bend, the point of tangency moves on the cone. Let us draw the circles made by all points of tangency. When the axis is located exactly in the middle, i.e., when the wagon is moving in a straight stretch of track, these circles on the two wheels attached to the same axis are equal. But when the axis is shifted, in a curved stretch, the circle on the inner wheel is smaller than the circle on the outer wheel. So we can consider that the wheels have vari­able radii. And since the radius of the inner wheel is smaller than the radius of the outer wheel, when the wheels are moving on the rails without skid­ding, the inner wheel makes a shorter ride than the outer wheel.

But why in a bend the pair of wheels is shifted over the rails? It turns out that physics is not involved. It’s just geom­etry, and also a very beau­tiful geom­etry! When the tracks bend, they cause a shift of the pair of wheels exactly as much as neces­sary so that the inner and the outer wheels roll without skid­ding.

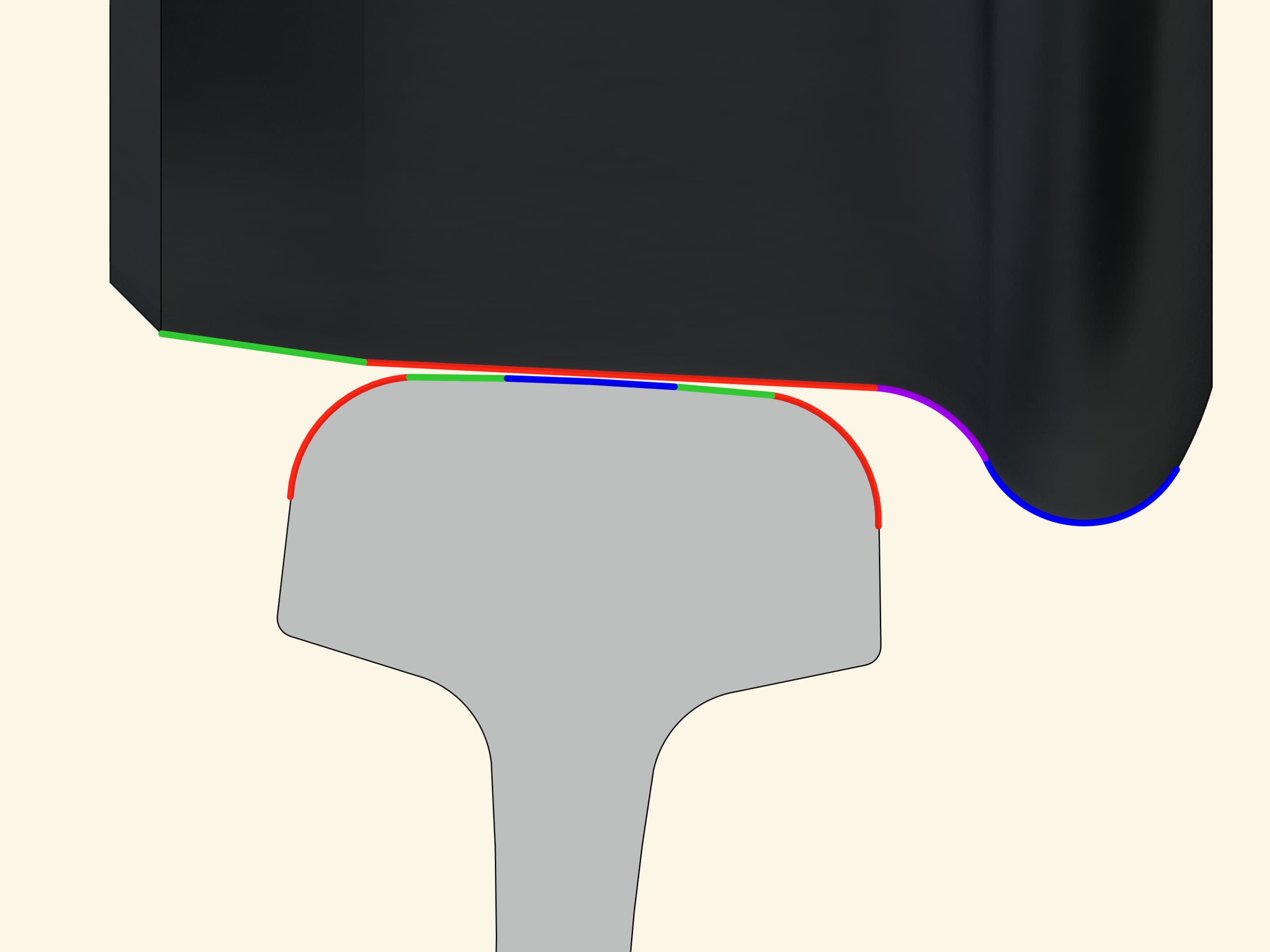
A good model must take into account the most impor­tant prop­er­ties of the objects under consid­er­a­tion and to neglect the details. Such is the model we have consid­ered, but in reality every­thing is more complex. According to the railway company, the surface of the wheel is composed of two trun­cated cones with slightly different open­ings angles. There is more­over a ledge, i.e., the wheel has an edge that prevents it from leaving the rails. The profile of the projec­tion is made of different arcs of circles. The profile of the rail, which in the model consisted of a circular arc, is in fact formed by the union of five different arcs of circles.

How to deal with a bend by a pair of wheels of the train is substan­tially different from how to deal by the ⁠⁠wheels of a car, but in reality, in either case plays a role that wonderful science which is the geom­etry.