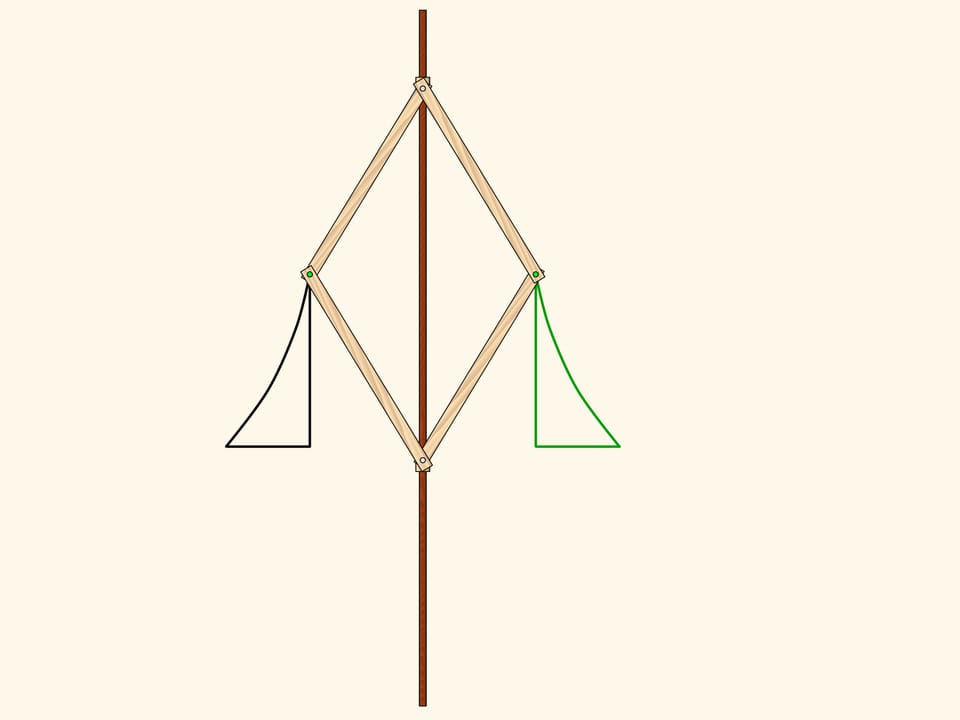
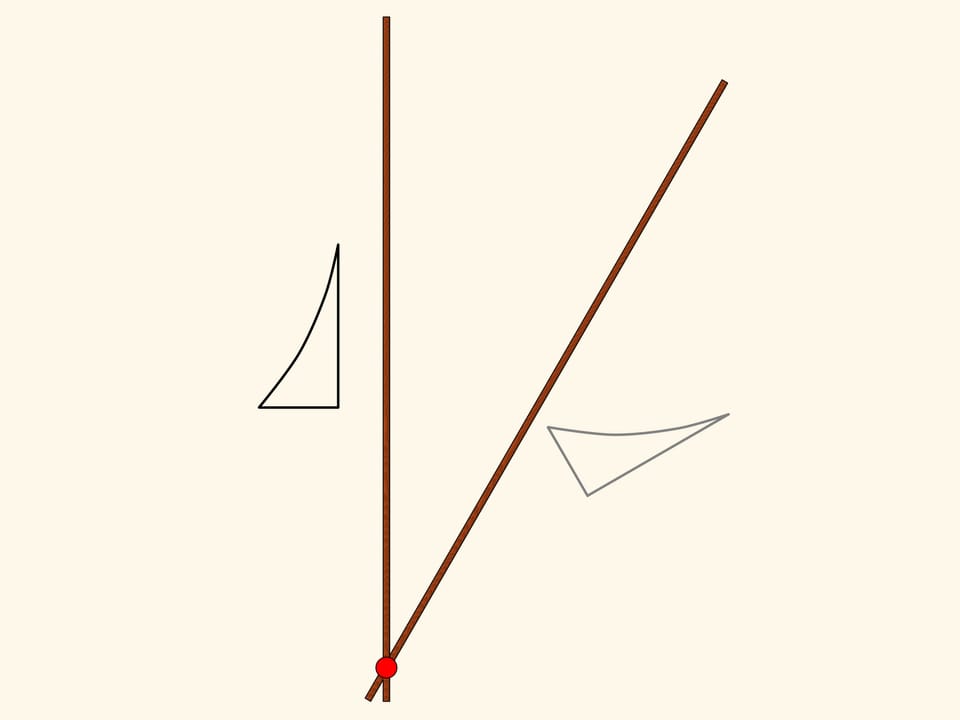
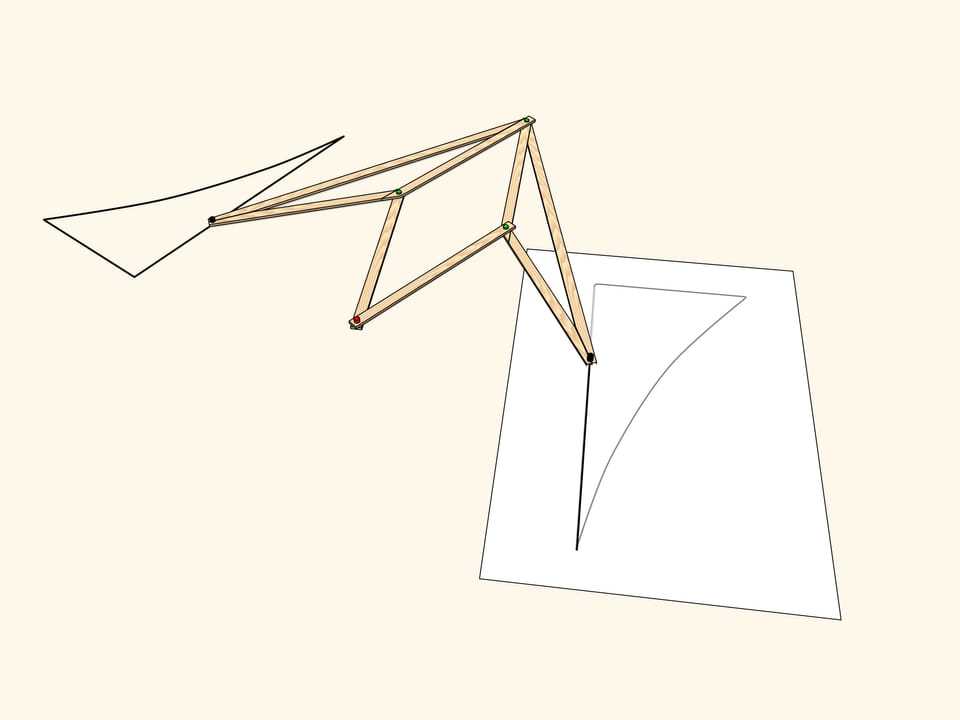
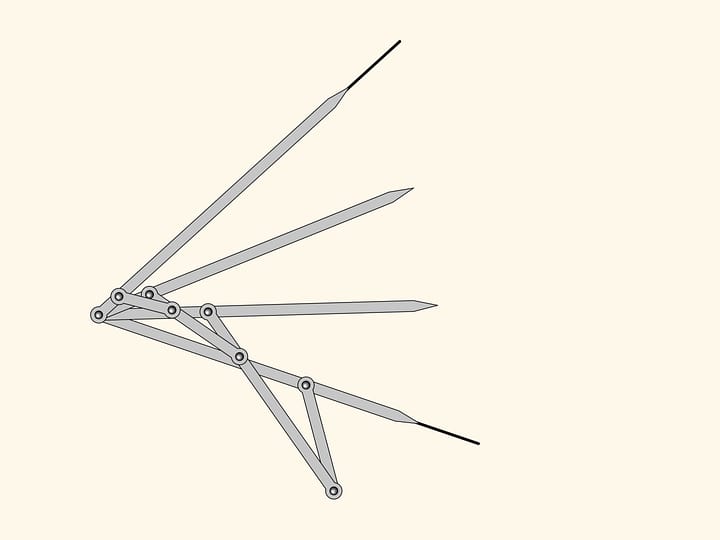
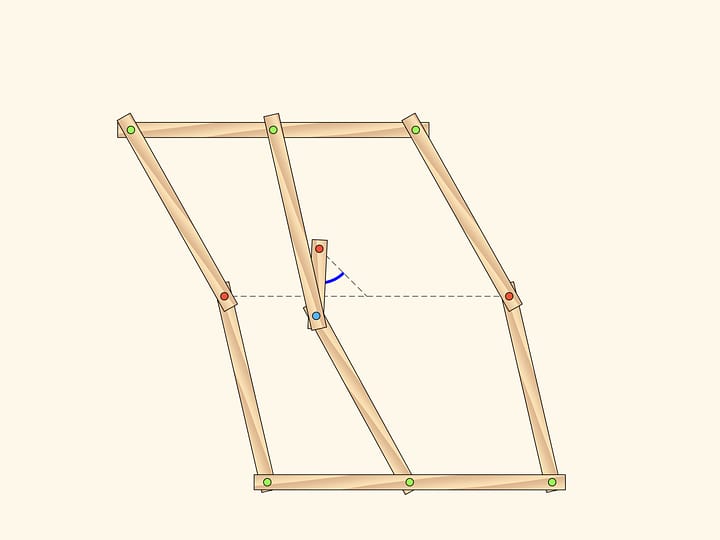
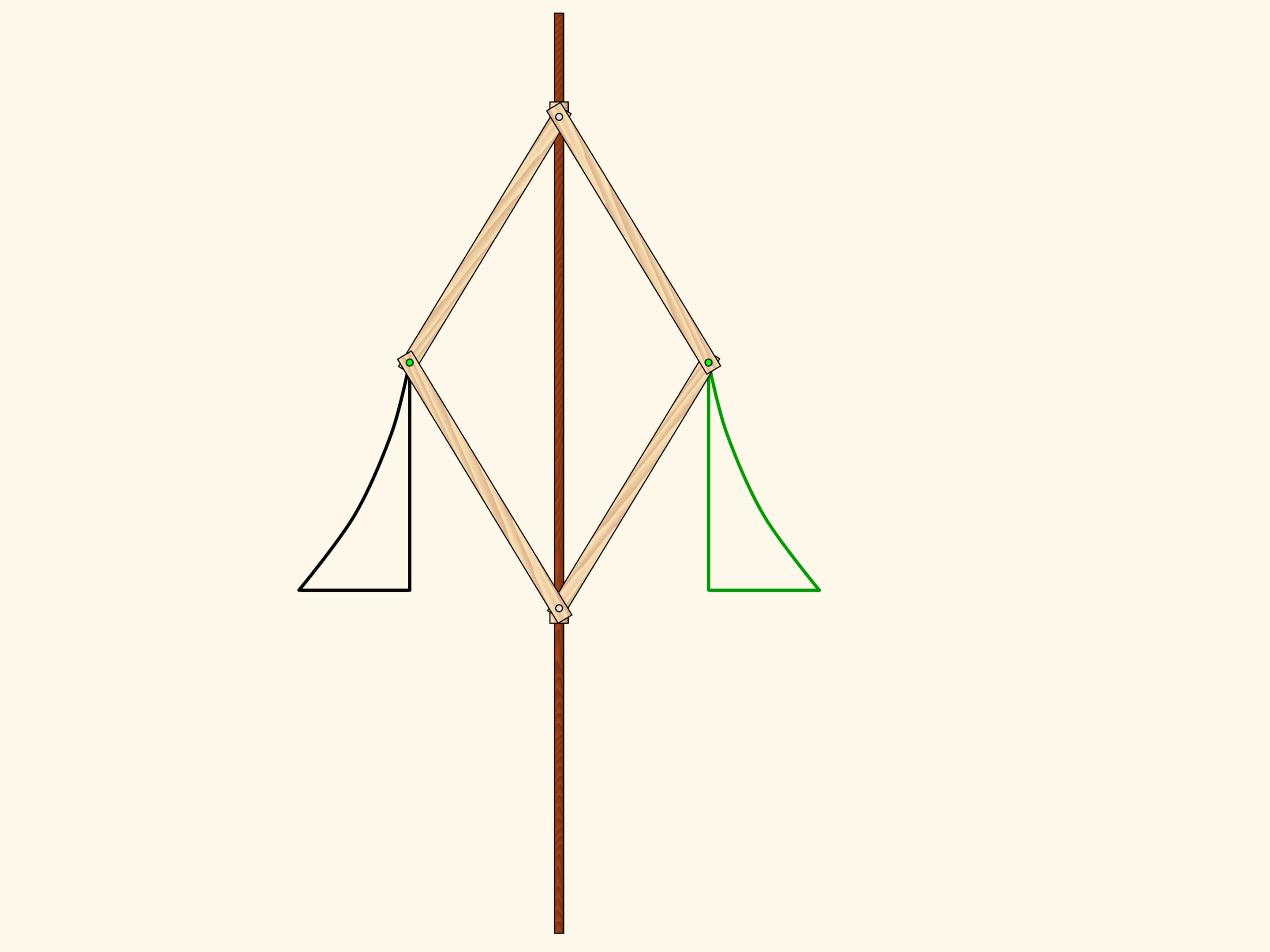
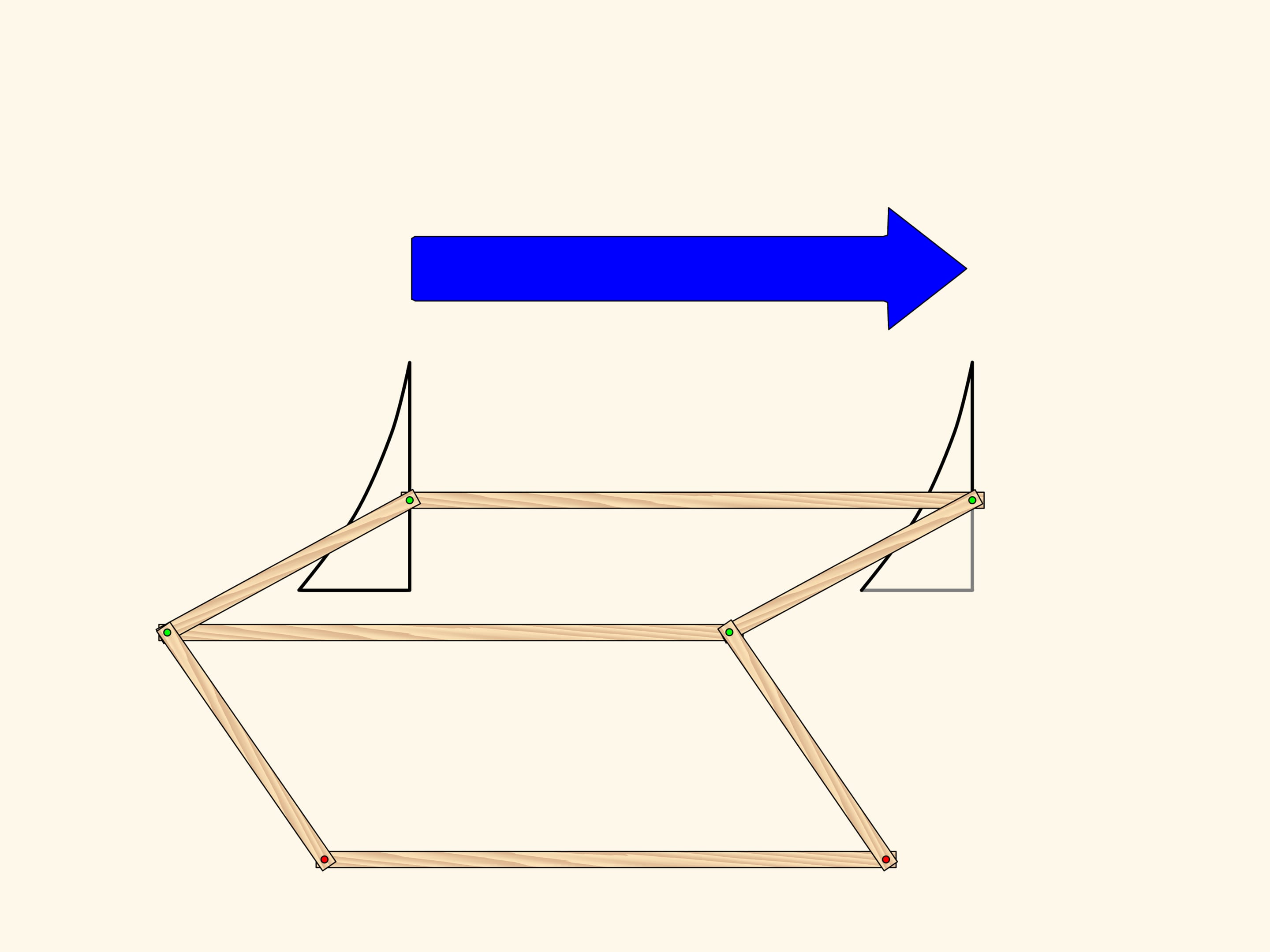
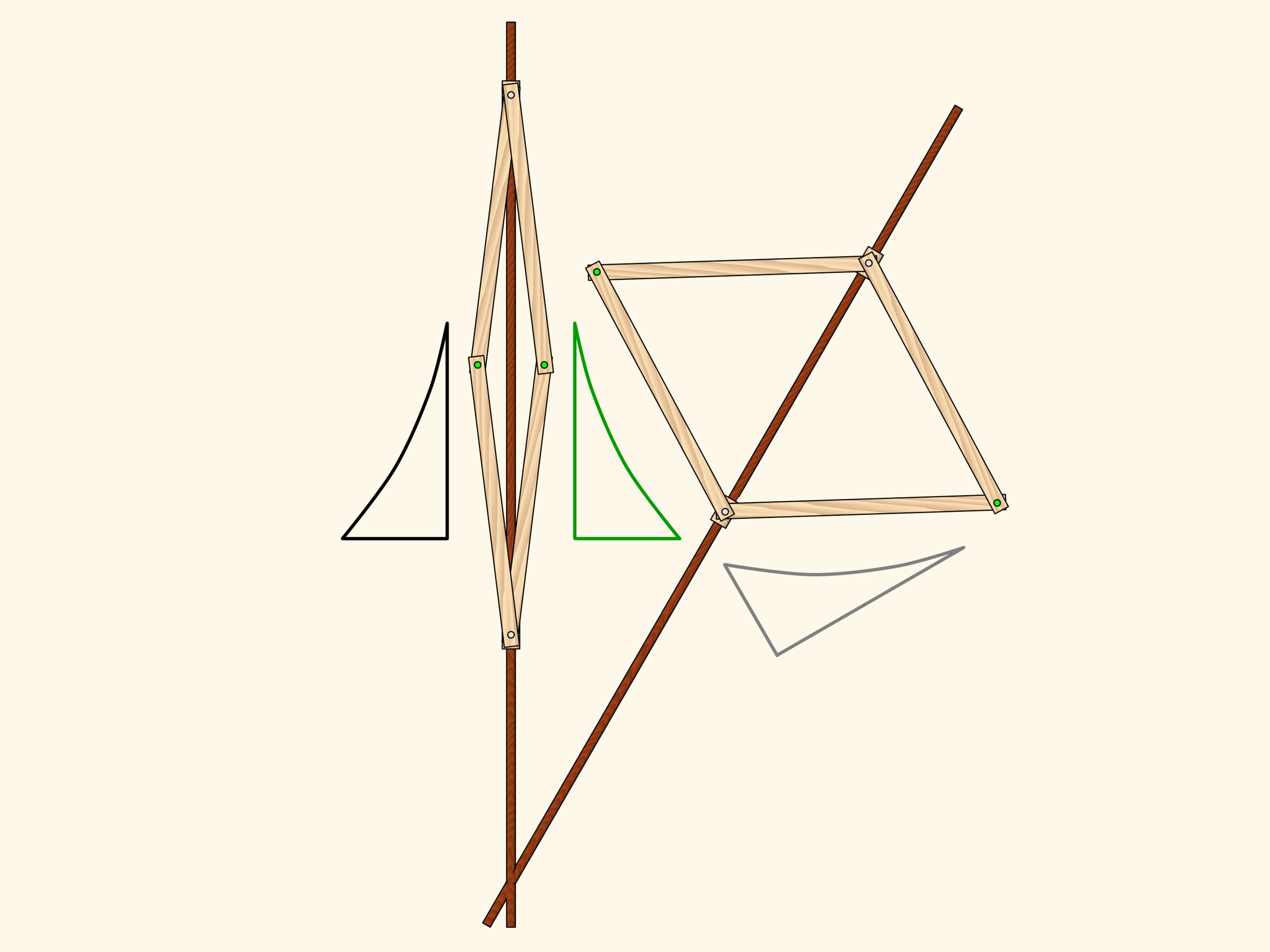
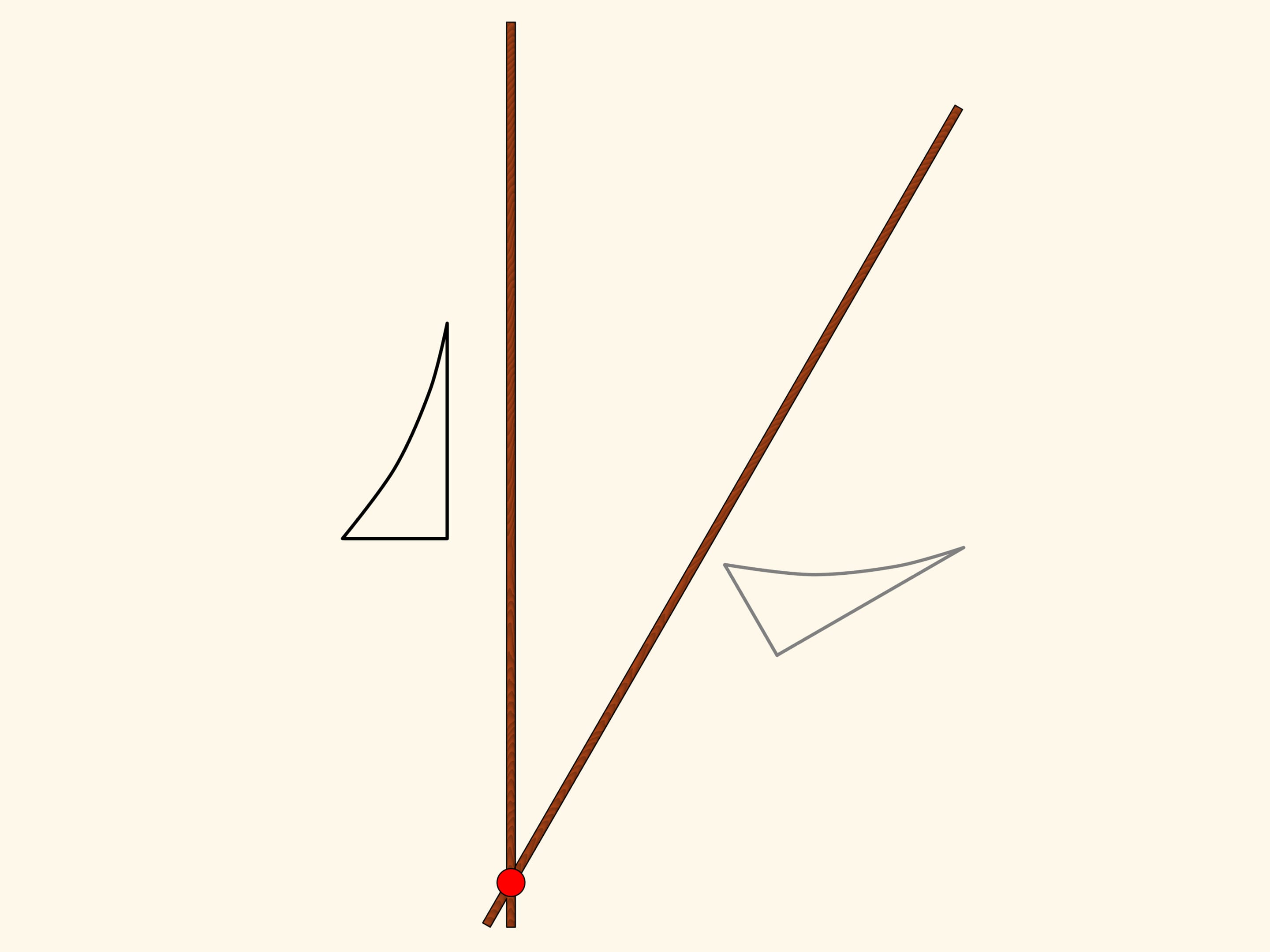
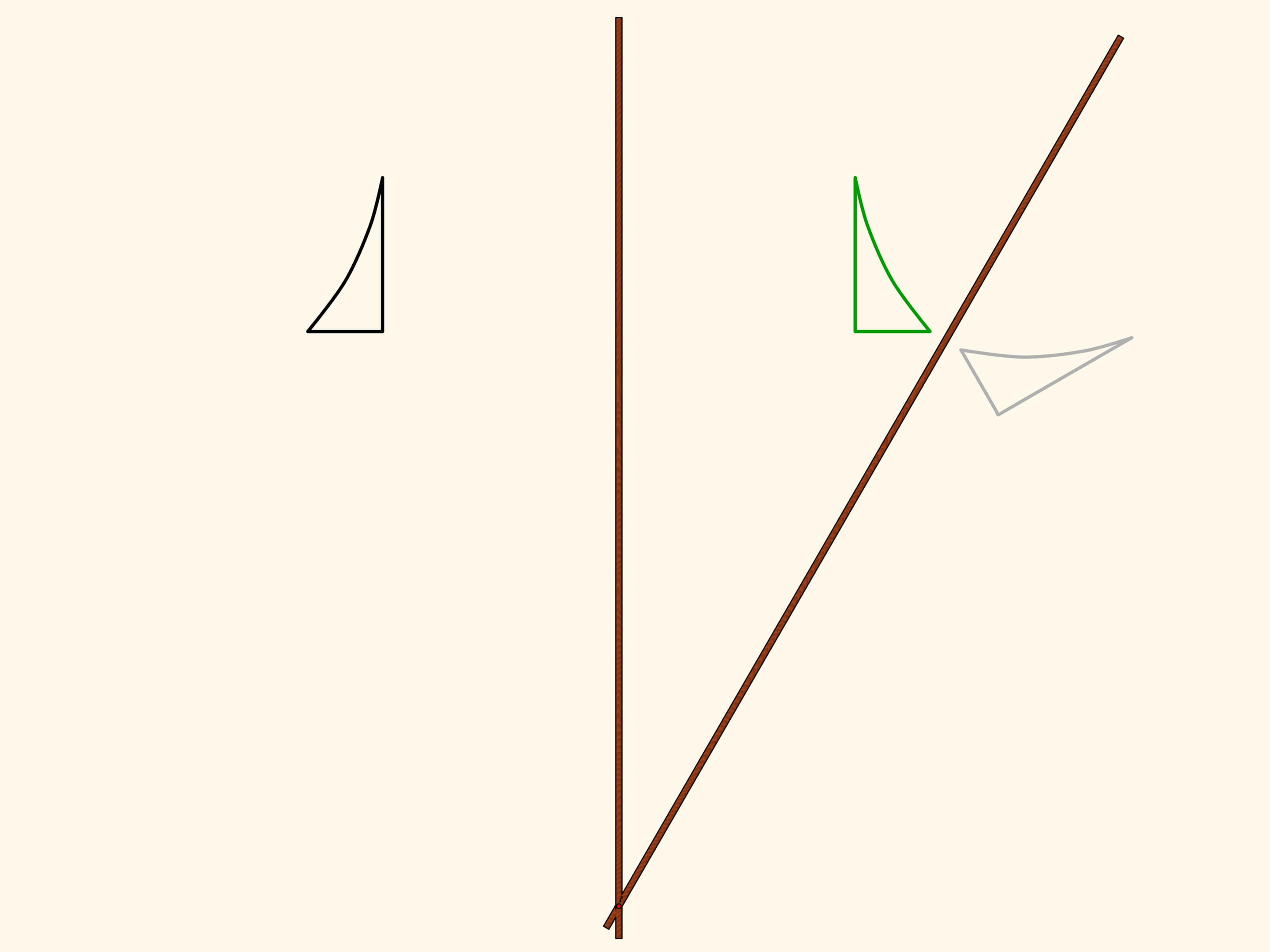
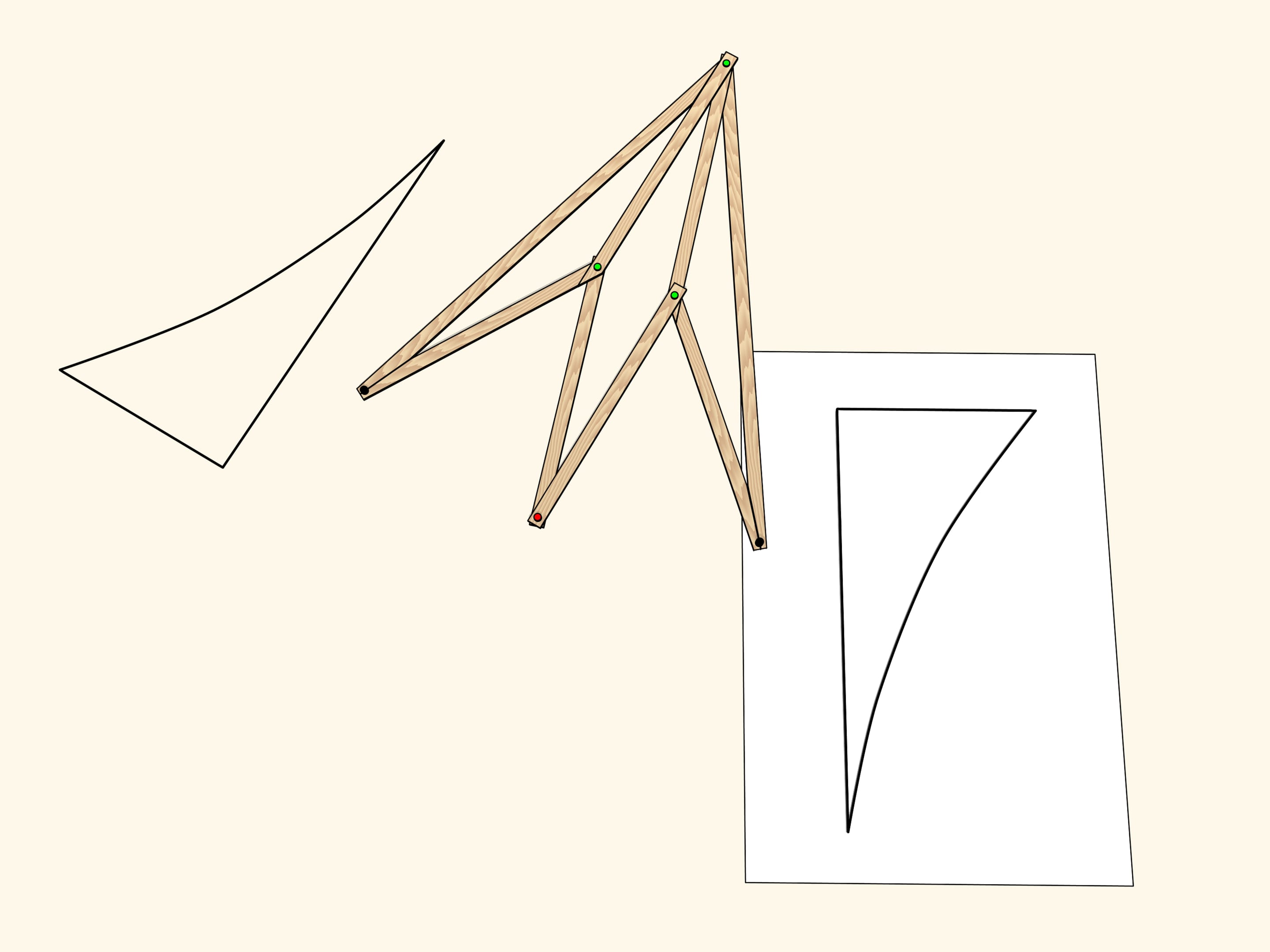
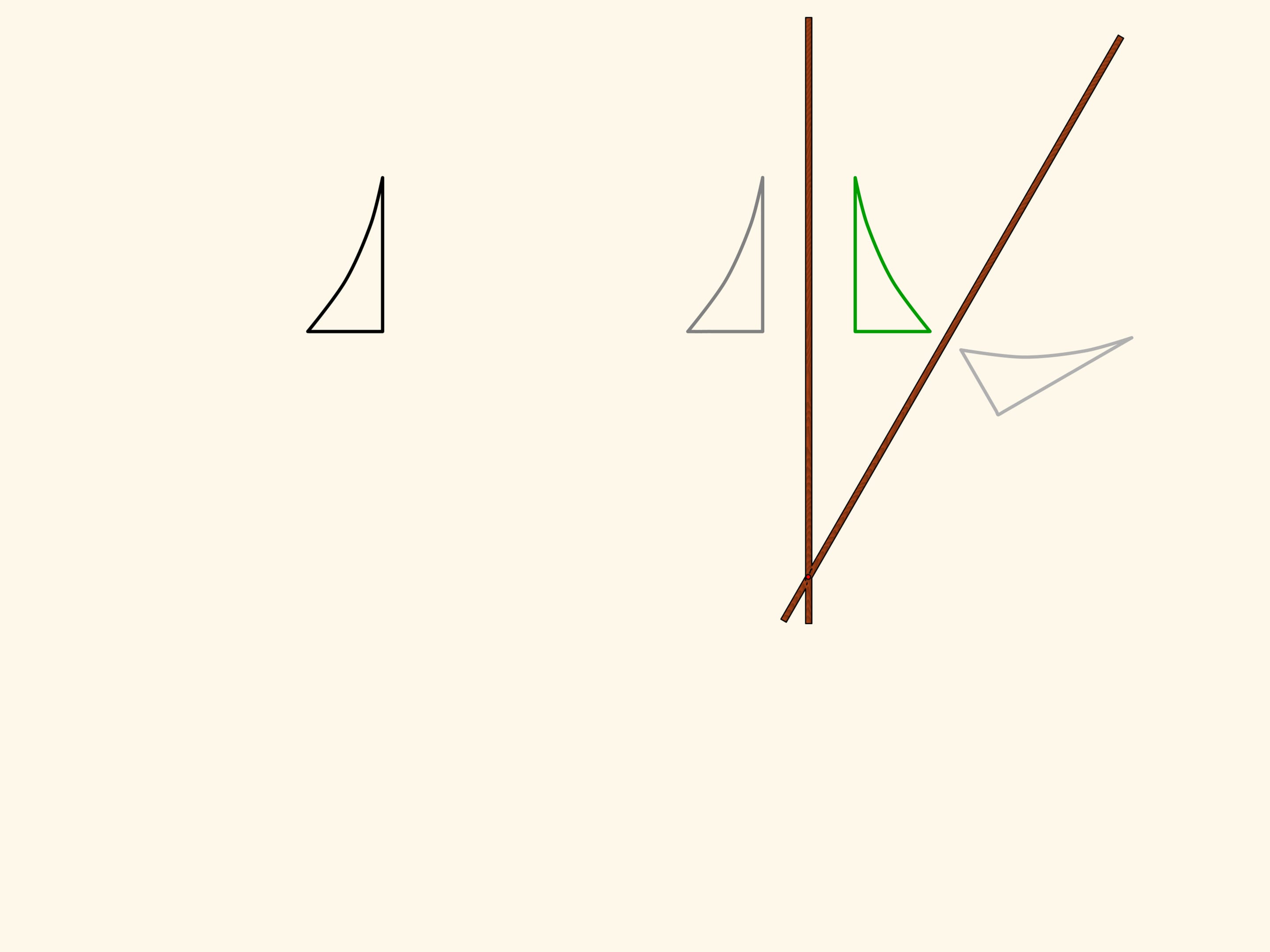A hinge rhomb, consisting of equal edges and using sliders that move on the fixed red rod, implements axial symmetry. Indeed, the location of one of the green hinges determines both the length of the opposite side of its triangle, and the opposite triangles are equal. That means that in any state of the mechanism two green hinges remain symmetric with respect to the red rod.
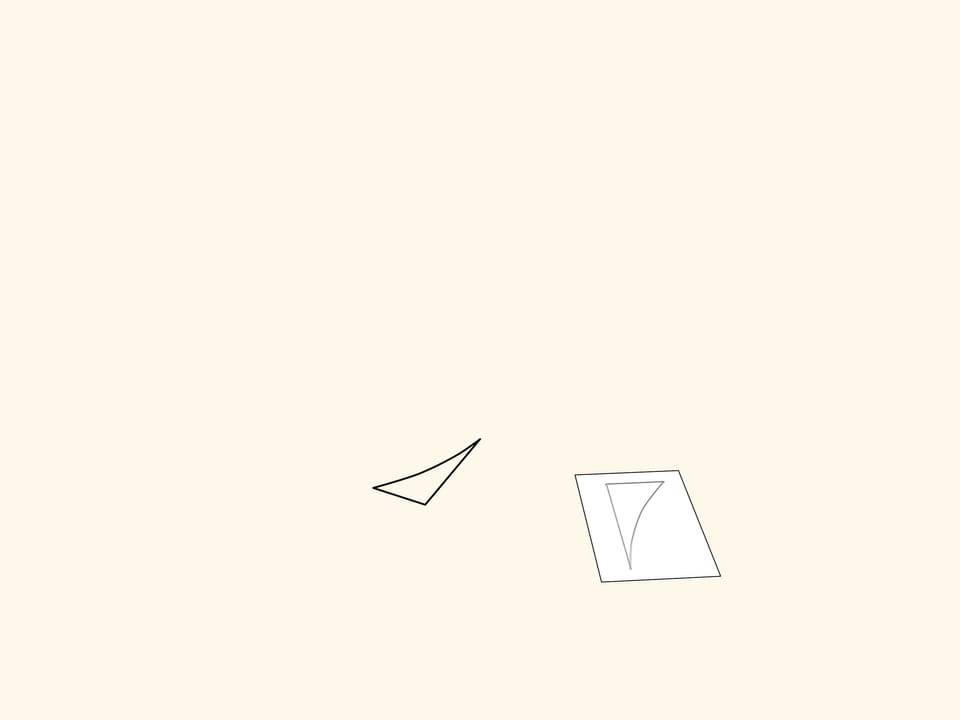
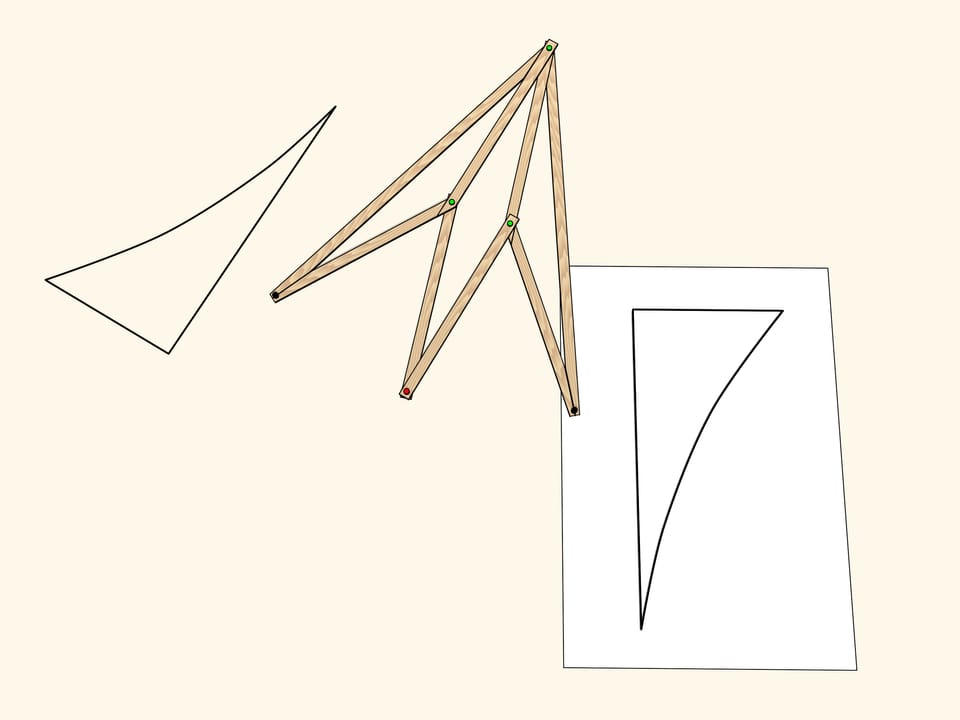
Consider a figure, curvilinear triangle, and look where it maps under the mechanism action. We get a symmetrical figure. It equals the original but is differently oriented. That is, if the plane was an infinitely large sheet of paper with the figure drawn on it, one would have to fold it along the symmetry axis and one part would be upside-down.
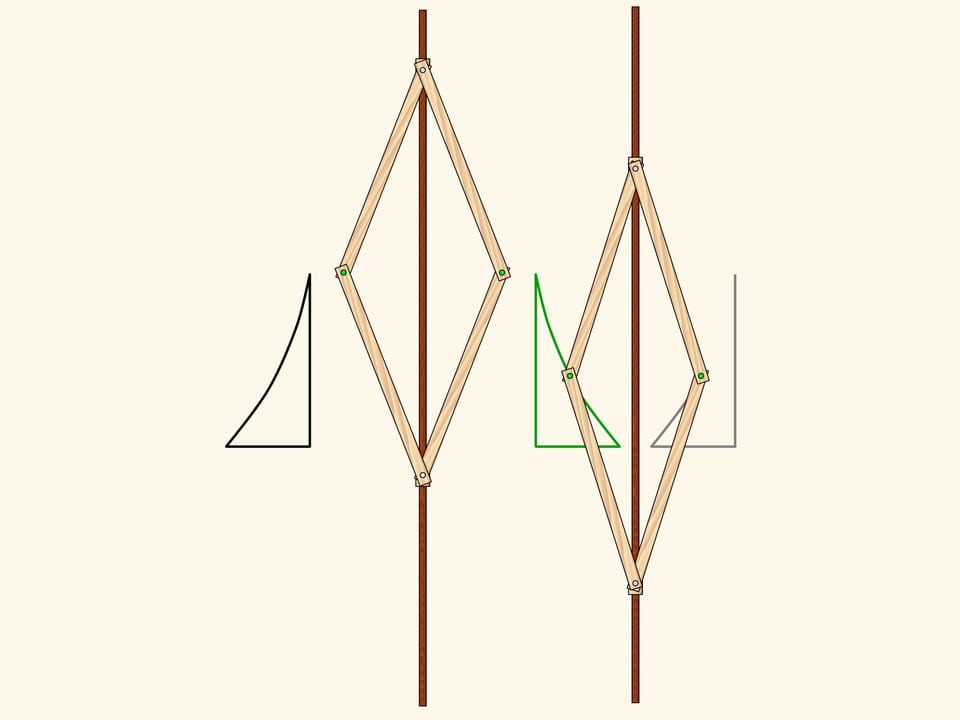
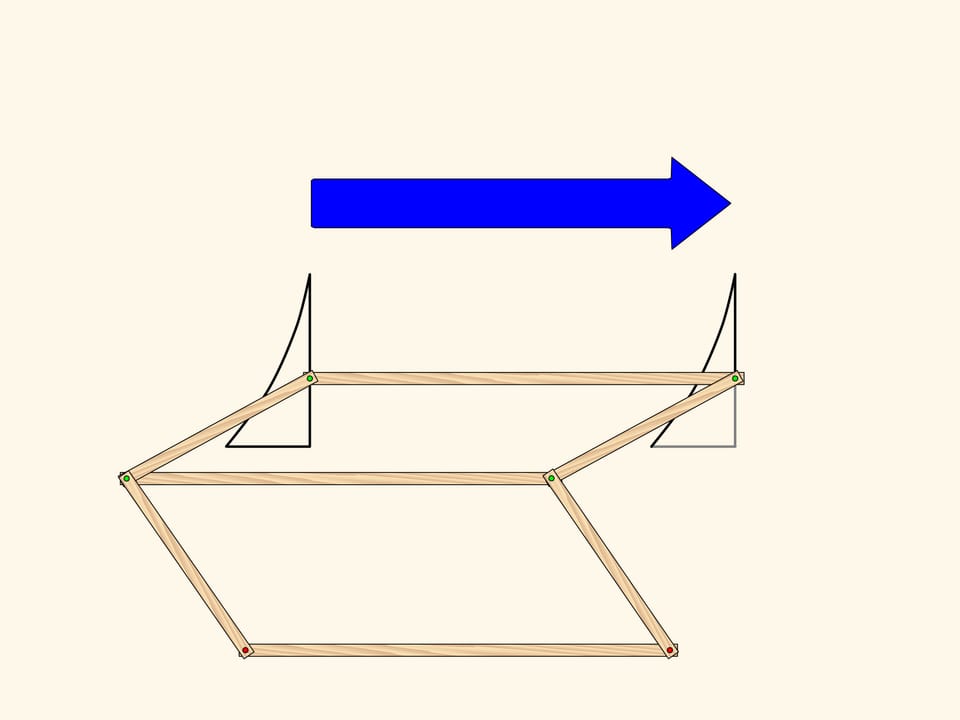
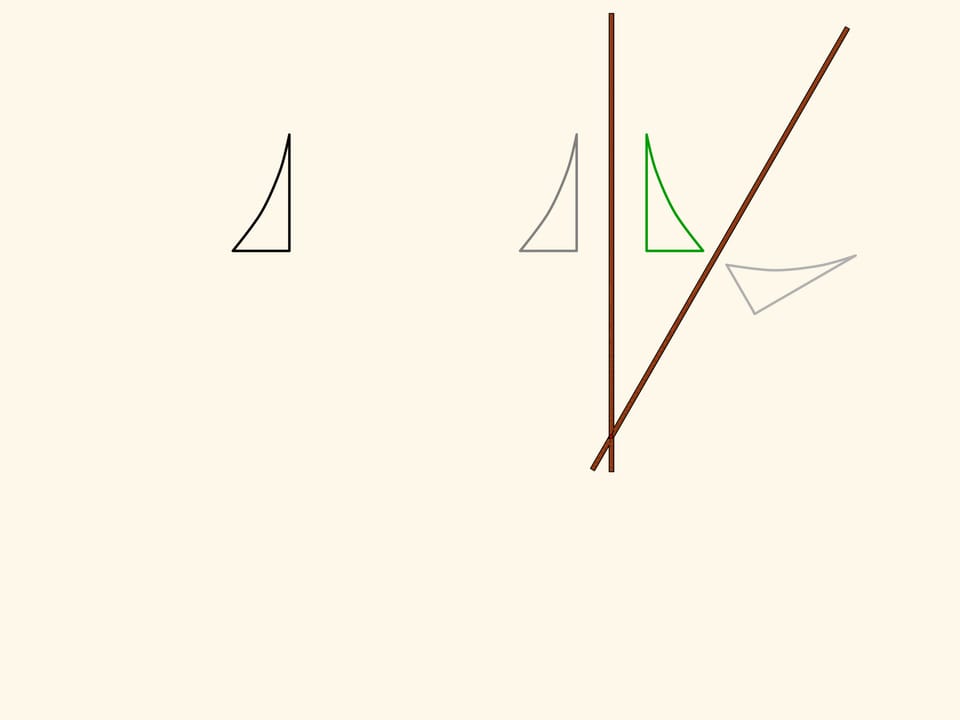
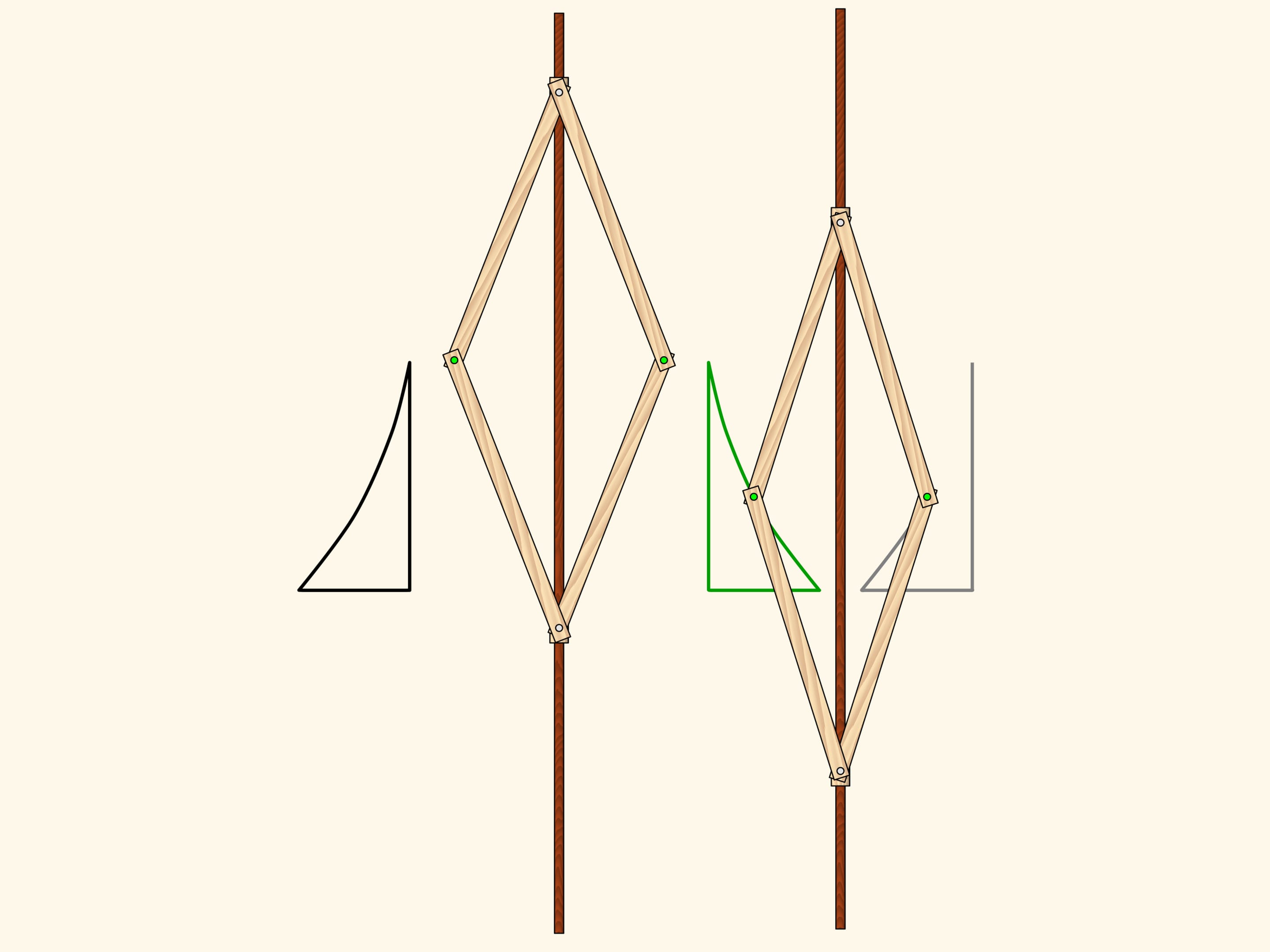
Apply a symmetry mechanism with a parallel axes to the triangle we obtained using the first one. The implements this plane transformation. So, the result of two axial symmetries with parallel axes is a shift. The converse is also true: any parallel transport can be decomposed into two symmetries with parallel axes. It's easy to see that such a decomposition is not unique.
Such a result of consecutive mappings is called a composition, and in terms of functions, a composed function. As in the analytical case, the result of a composition can be obtained with consecutive actions or after some simplifications. The transformed object may be totally different from the original.
And what happens if the symmetry axes are not parallel?
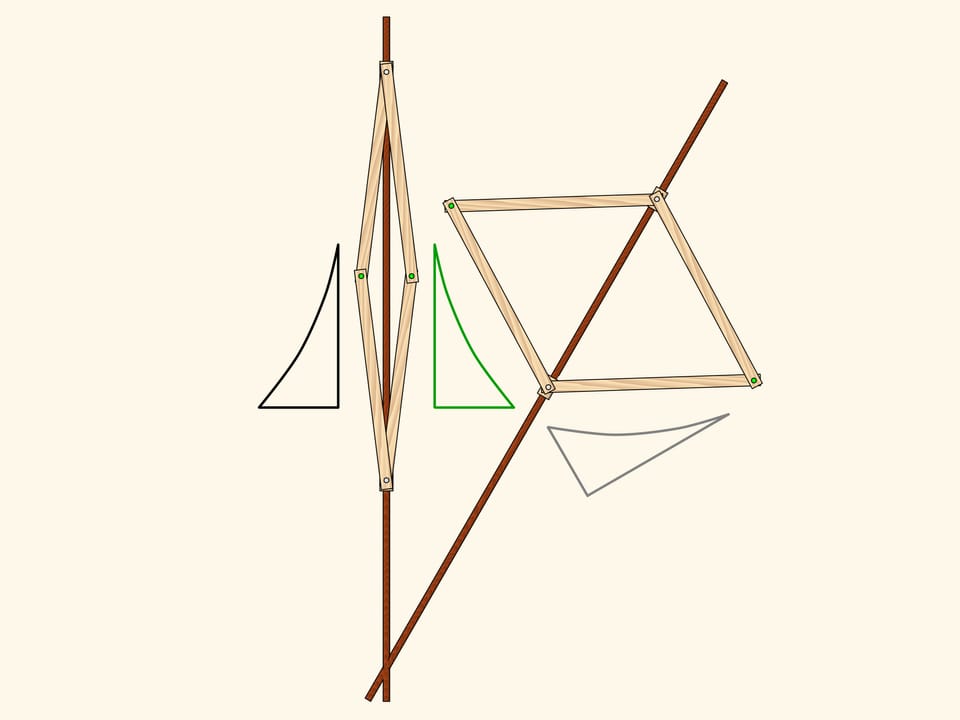
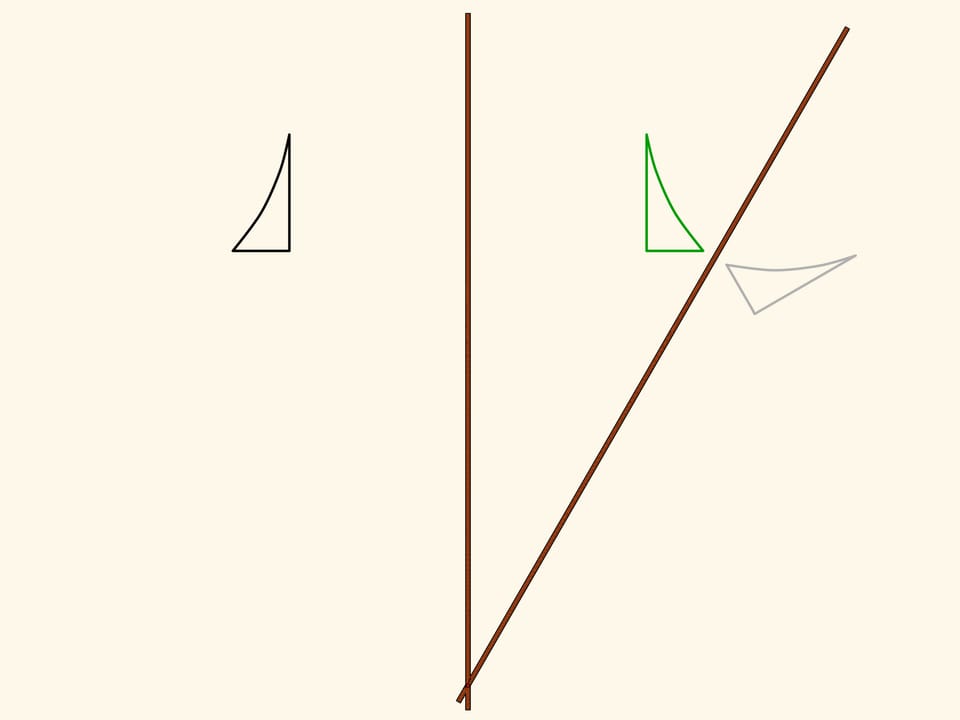
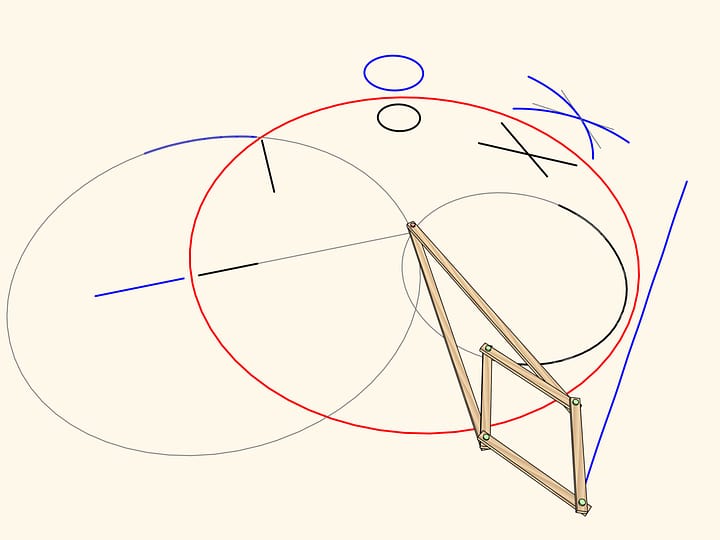
The composition of two axial symmetries with non-parallel axes is a rotation centered at the point of intersection of the axes. And the angle of rotation is twice bigger than the angle between the axes. As in the case of the shift, the converse is true: every rotation can be decomposed into a pair of axial symmetries.
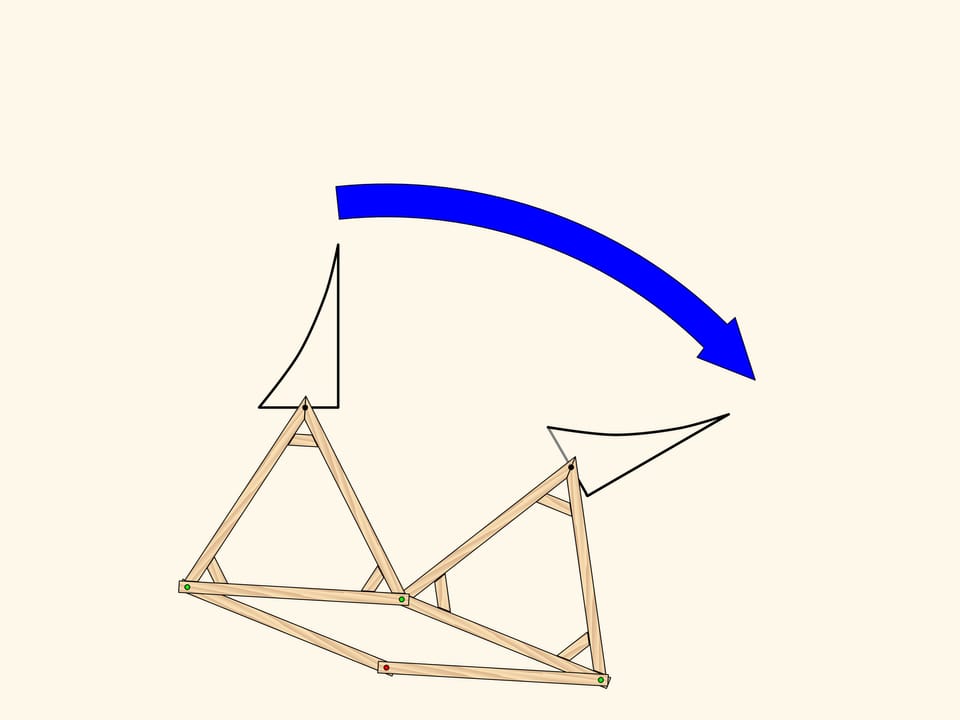
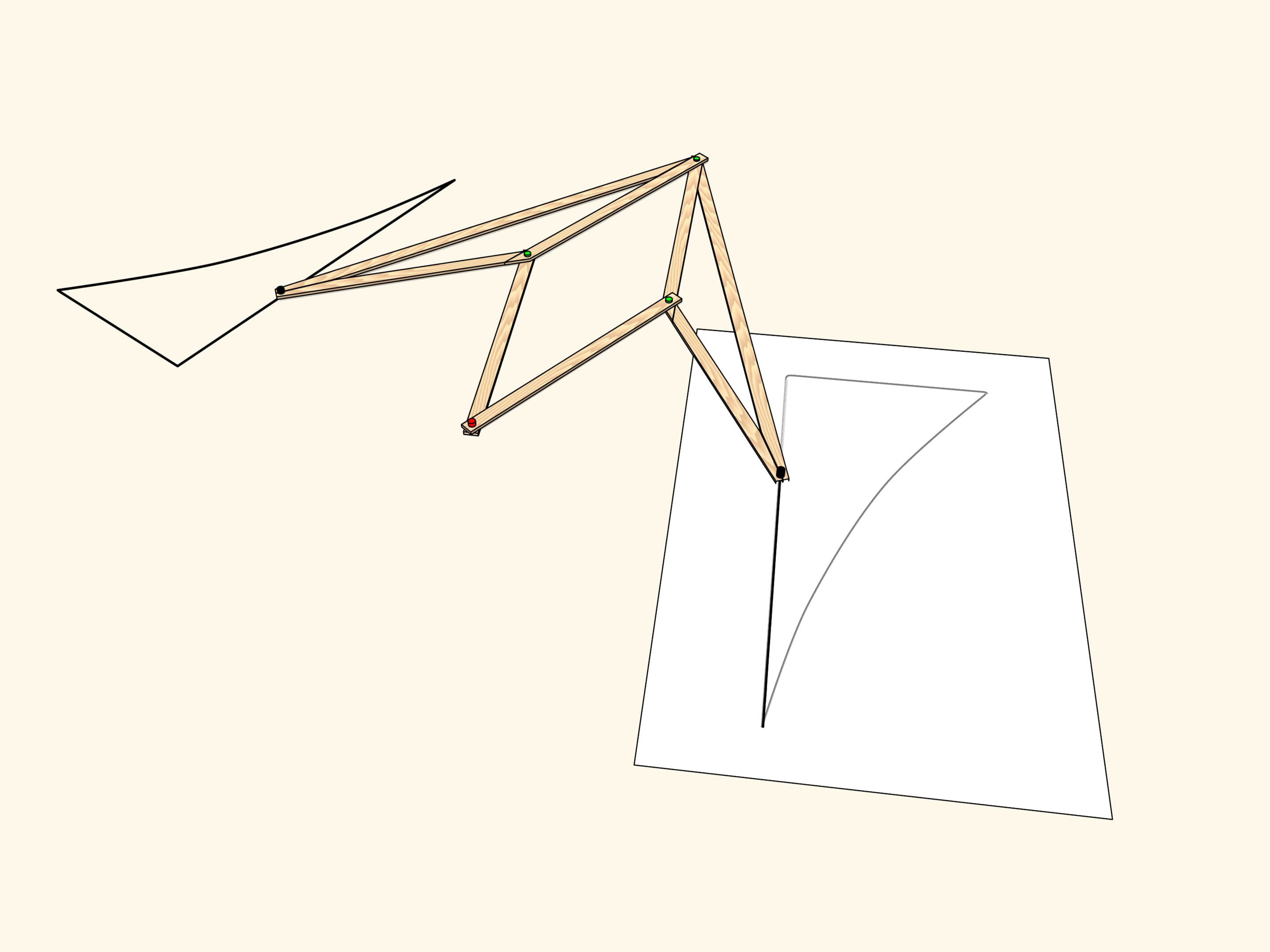
A linkage based on a rhomb implements rotation transformation.
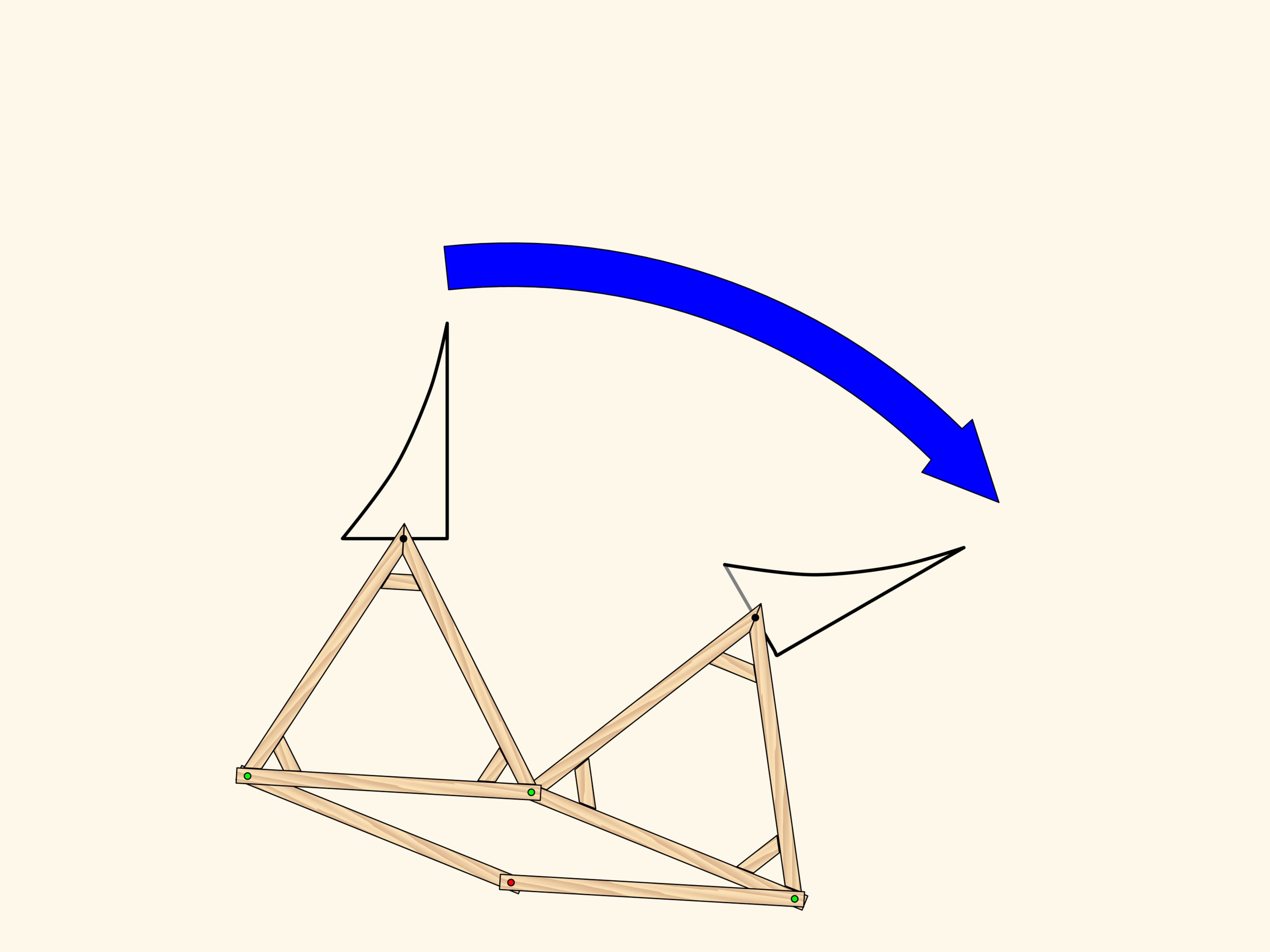
What if we apply consecutively a translation and a rotation? Can we match the result with the source?
Decompose the rotation into two symmetries. On the picture we can see that the stage of obtaining the gray triangle and applying a symmetry can be replaced with a single symmetry. An what is left, the composition of two axial symmetries with non-parallel axes, is just a rotation as we know.
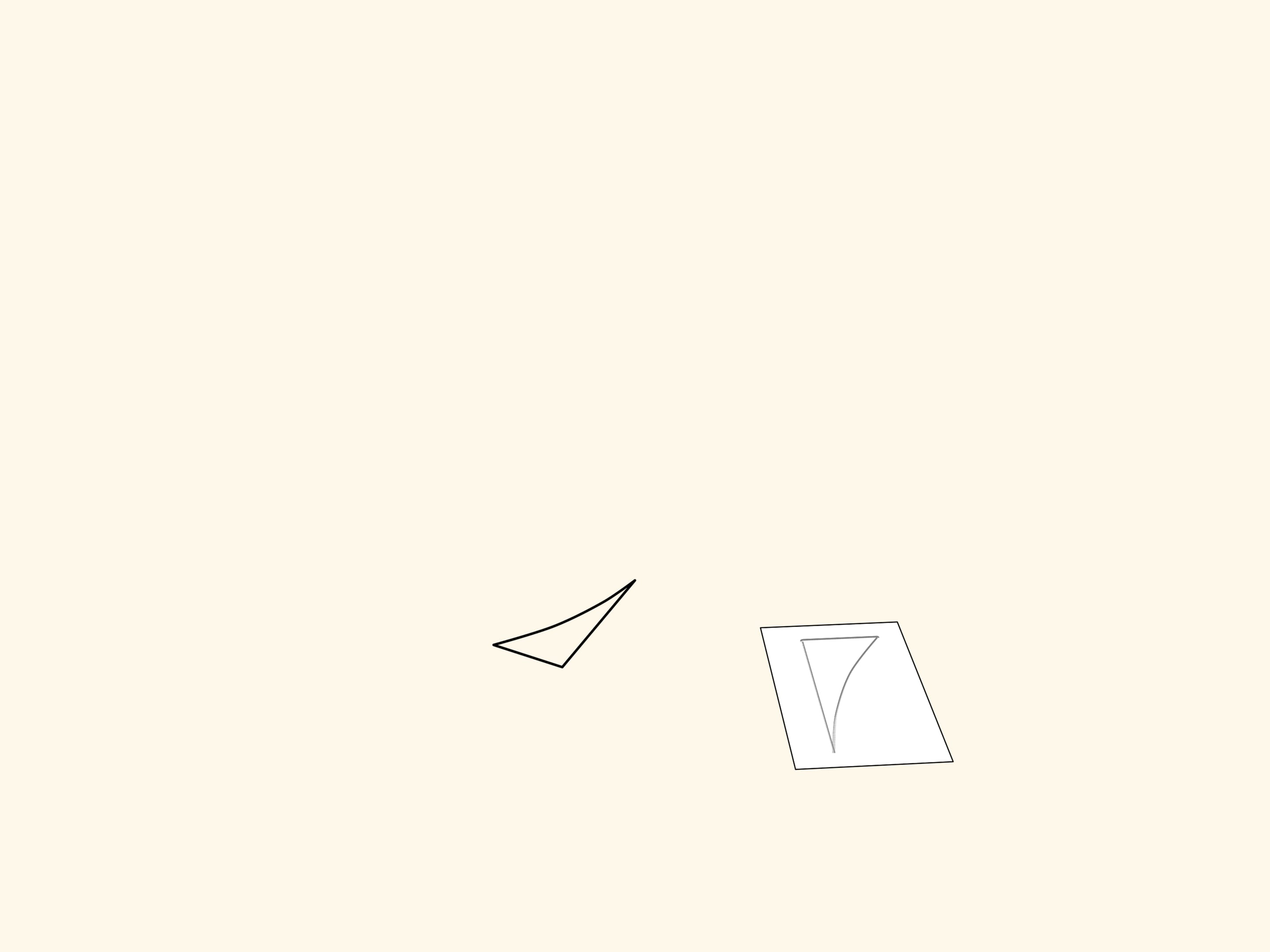
Draw the triangle on a table. Put a sheet of paper over it and outline the figure. Lift the sheet and just a rotation around some point to some angle!